新课标背景下“统计与概率”的变化
【摘 要】 《义务教育数学课程标准(2022年版)》新增“四分位数与箱线图”内容,箱线图是统计学中的专用名词,这便给教师的教学带来新挑战.从大数据时代发展的需要与数学课程内容发展的需要两方面分析增加该内容的教育价值;介绍箱线图的定义、画法、应用,通过实例说明箱线图在计算量较小与直观展示数据分布情况的优势,并阐述新增“四分位数与箱线图”给笔者带来的教学启示.
【关键词】 新课标;统计与概率;四分位数;箱线图;数据观念
1 研究缘起
《义务教育数学课程标准(2022年版)》在“统计与概率”领域新增“会计算四分位数,了解四分位数与箱线图的关系,感悟百分位数的意义”[1],这与《普通高中数学课程标准(2017年版)》“统计与概率”领域中“结合实例能用样本估计百分位数,理解百分位数的统计含义”相衔接,由此可见,此次2022版新课标非常重视初中、高中“统计与概率”领域内容的衔接,学生在初中阶段对四分位数、百分位数、箱线图的理解会直接影响高中阶段“统计与概率”领域的学习.下文将分析初中阶段增加该内容带来的教育价值;介绍箱线图的定义、画法、应用,并阐述新增“四分位数与箱线图”内容给笔者带来的教学启示.
2 “四分位数与箱线图”的教育价值
2.1 大数据时代发展的需要
2012年7月,联合国发布《大数据促发展:挑战与机遇》白皮书,提及“大数据时代已然来临,大数据的产生会给社会诸多领域带来深远影响.随着大数据时代的飞速发展,数据分析素养正悄无声息成为现代公民社会生存的关键能力”.箱线图是统计图中的一种,应用箱线图能有效解决不同领域的实际问题,例如,杨帆[2]等应用箱线图对大曲质量进行分析;吴九牛[3]等应用箱线图提出一种插值方法检测机动车尾气NOx气体的含量;鲁俊[4]等应用箱线图对新生儿出生缺陷的发病率进行预测,等等.大数据已经成为继科学实验、理论科学与计算科学的第四范式[5].
2.2 数学课程内容发展的需要
2022版新课标在“统计与概率”领域学业要求中新增“知道百分位数和四分位数,能計算一组数据的四分位数,知道箱线图可以直观反映数据分布的信息”.首先,回顾两个能刻画一组数据离散程度的特征值——极差、方差,数据的离散程度是数据分布的特征之一,它反映的是每一个数值与“中心值”的偏离程度.极差在一定程度上刻画了一组数据的离散程度,但是它仅反映出这组数据的波动范围,不能反映中间数据的离散程度.比较两组数据的离散程度时,若两组数据的平均数、极差都相等,此时就不能较好地区分两组数据的离散程度,于是引入方差,方差是刻画这组数据中每一个数值与“中心值”的离散程度,值得注意的是,方差的“中心值”是平均数,但是,平均数容易受到极端值的影响,所以有时用平均数作为“中心值”会出现“失真”现象.通常情况下,极差、方差能够刻画一组数据的离散程度.通过箱线图也能够观察出一组数据的离散程度,既然义务教育阶段有能够刻画一组数据离散程度的特征值,为何还要引入箱线图呢?箱线图是统计图中的一种,通过箱线图能够直接观察出这组数据中的异常值及数据的离散程度,且计算量较小,这样就弥补了以往教学中从“形”上直观感知数据离散程度的“遗憾”.箱线图的“中心值”是这组数据的中位数,相对而言,用箱线图直观描述这组数据的离散程度会比较合理;当对比多组数据的离散程度时,应用箱线图会更方便,也会更加直观.下面,介绍箱线图的定义、四分位数与百分位数、箱线图的作图步骤,并以笔者两个班级的期末考试成绩为例,说明箱线图在实际中的应用.
3 箱线图、四分位数与百分位数
3.1 箱线图的定义
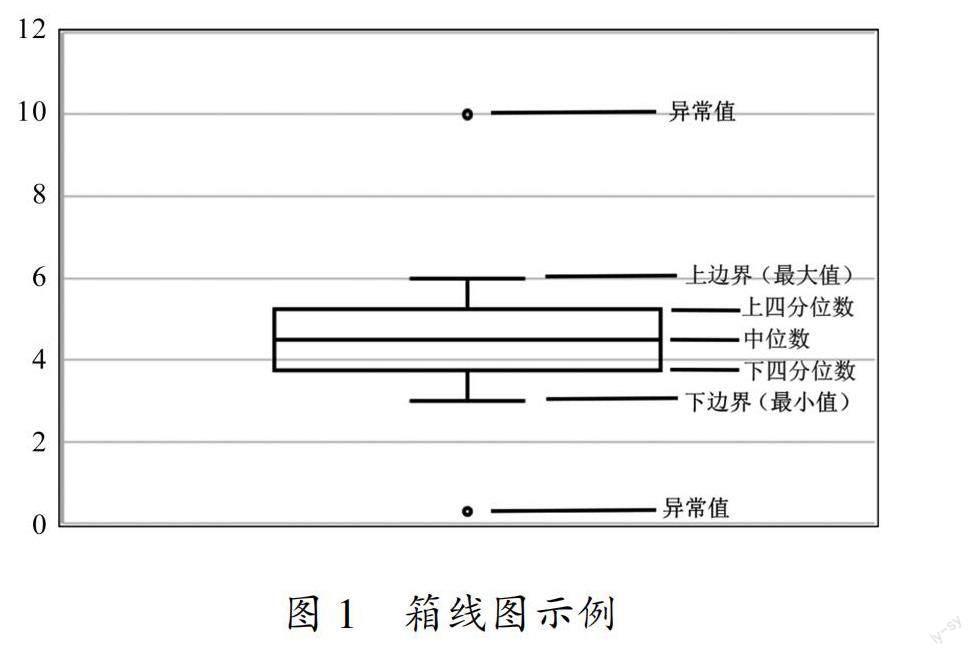
1977年,美国统计学家约翰·图基提出一种用于显示数据分布特征的统计方法——箱线图,箱线图的形状形如箱子,因故得名.箱线图是一种利用最小值、下四分位数、中位数、上四分位数和最大值来描述数据分布特征的统计图[6],这也是四分位数与箱线图的关系.
3.2 四分位数与百分位数
什么是四分位数呢?首先需要了解百分位数,因为四分位数是在百分位数上建立起来的.百分位数又称百分位分数,它是一类统计量,把一列数从小到大排列,并计算相应的累计百分位,则某一百分位所对应的数就称为这一百分位的百分位数.具体来说,有一组数据按照从小到大顺序排列,用99个数值把这组数100等分,这99个数值就称为百分位数,为了表示方便,用P1,P2,…,P99表示第1、第2、……、第99百分位数,显而易见,P50表示这组数据的第50百分位数,即中位数;中位数将这组数据分为两个部分,将这两组数据分别记作S,T,用P25,P75分别表示S,T的中位数,所有数据中,小于或等于P25的数占25%,小于或等于P50的数占50%,小于或等于P75的数占75%,那么P25,P50,P75就把这组数的个数平均分成四份,P25,P50,P75这三个数值称为四分位数,特别地,P25称为下四分位数,P75称为上四分位数,这也是四分位数的计算方法.2022版新课标在“统计与概率”的学业要求中指出,“知道百分位数和四分位数,能计算一组数据的四分位数,知道箱线图可以直观反映数据分布的信息”,并且新课标在附录部分以一个实例(例86)让学生感悟箱线图的学习价值.在初中学段,对于百分位数的学业要求仅在“知道”层面,学生到高中学段,会详细学习如何计算第几百分位数,此文不再赘述第几百分位数的计算方法,感兴趣的读者可查阅人教A版高中数学必修第二册(2019年版)“9.2.2总体百分位数的估计”.
3.3 箱线图的作图步骤
通过上文描述可知,箱线图是一种利用最小值、下四分位数、中位数、上四分位数和最大值来描述数据分布特征的统计图.箱线图不仅需要计算四分位数,还需要计算下边界(最小值)、上边界(最大值)、异常值,但是这些特征值的计算量都比较小,箱线图示例如图1所示.上文介绍过四分位数的求法,这里不再赘述,下面介绍下边界(最小值)、上边界(最大值)、异常值的计算方法,计算这三个特征值时需要先计算四分位差(简称“IQR”),四分位差(IQR)=上四分位数(P75)-下四分位数(P25),下边界(最小值)=P25-1.5IQR,上边界(最大值)=P75+1.5IQR,规定大于上边界(最大值)或小于下边界(最小值)的值都称为异常值.箱线图的作图步骤如下:
1)将一组数据按照从小到大顺序进行排列;
2)找到这组数据的中位数,中位数将这组数据分为两个部分,再继续找出这两组数据的中位数,于是得到下四分位数、中位数、上四分位数;
3)计算:四分位差(IQR)=P75-P25,下边界(最小值)=P25-1.5IQR,上边界(最大值)=P75+1.5IQR;
4)画出数轴,画出上边界、上四分位数、中位数、下四分位数、下边界、触须线、箱体,标出异常值(通常用空心圆表示).
3.4 箱线图的应用
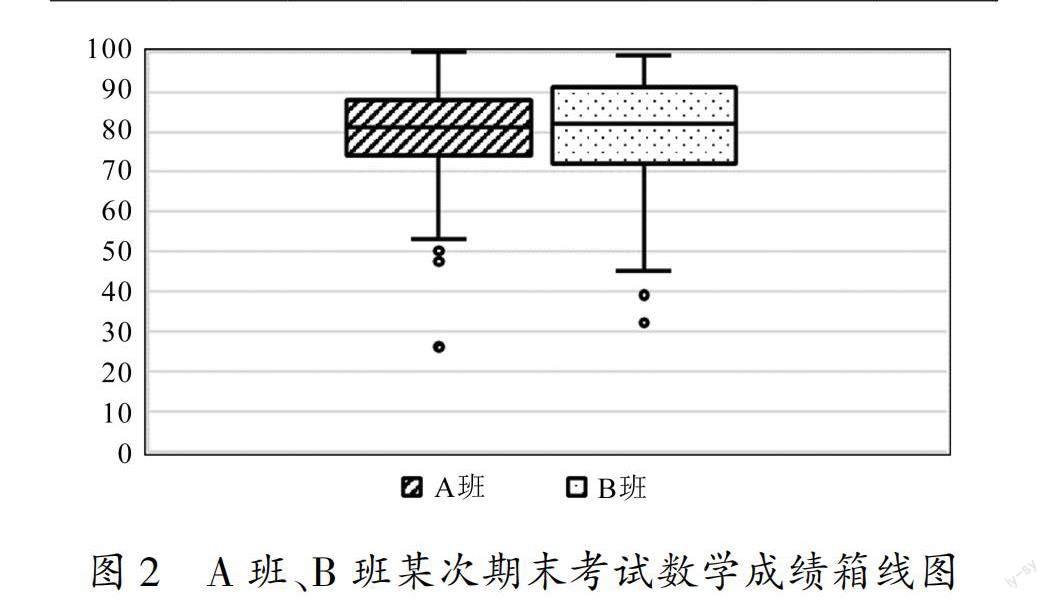
下面,以笔者任教的两个班级某次期末考试数学成绩(表1、表2)为例,应用箱线图对两个班级学生的成绩进行分析.
笔者所在学校是均衡分班,每个班级的平均水平相当.A班、B班本次期末考试数学成绩的平均分分别是77.98分、78.07分,从平均分的视角来看,两个班级的平均水平相当;但是从中位数的视角来看,能够从箱线图上直观看出B班数学成绩的中位数高于A班,B班平均水平略高一些.按照上述画箱线图的过程,绘制出A班、B班本次期末考试数学成绩箱线图(图2),不用计算A班、B班期末数学成绩的方差,通过箱线图可以直接观察出A班的箱体高度比B班的箱体高度矮,说明A班学生的数学成绩波动性小,数据更聚集,大部分学生的成绩相差不大;相比较而言,B班学生的数学成绩波动性相对较大,数据也就相对较为分散,B班级学生在数学学科上的发展有两极分化的趋势.从箱线图上显示出A班学生的数学成绩有3个异常值,B班学生的数学成绩有2个异常值.通过上述对数据的分析,提示笔者需要关注B班级学生两极分化的原因,寻找缩小B班级学生内部差距的策略,后续教师要根据班级情况进行差异化教学,避免出现“两班一教案”现象,同时也需要关注异常值所对应的学生,要给他们更有针对性的学习建议.
4 教学启示
4.1 善用统计图(表)描述数据,顺应时代变革
数据观念包括数据感知力、数据处理能力、数据的质疑能力[7],其中,能够运用统计图(表)整理、描述数据是数据处理能力的具体表征.初中数学教材中常见的统计图(表)有条形统计图、扇形统计图、折线统计图、散点图、频数(率)分布表、频数(率)分布直方图,到高中学段学生还会学习茎叶图,《义务教育数学课程标准(2022年版)》中新增箱線图内容,这并非偶然,上文介绍可知,箱线图对各个领域的数据分析体现出重要的应用价值,新增该内容是顺应大数据时代变革的需要.箱线图具有计算量较小与直观展示数据分布情况的优势,还能够快速发现一组数据的异常值,尤其是对多组数据的分布特征进行比较时,更能凸显出箱线图的优势.但是,箱线图也不是“万能图”,箱线图仅从宏观层面展示数据的分布情况,如果要对数据进行更精准的分析,还需要借助其它统计图(表),例如,上文应用箱线图分析两个班级的数学考试成绩,只是对数据的分布情况进行了大致分析,如果还要更精确地分析两个班级的成绩,课堂上可以借助该实例引导学生结合柱状图(图3)进行精确分析,从柱状图上能直观看出B班级90分以上的学生比A班级多4人,提醒教师要注重A班级优等生的培养,B班级50分以下的学生比A班级多2人,教师要关注B班级薄弱生的指导,结合柱状图能够更进一步对两个班级的数学成绩进行分析,能够更精准地找到本班级数学成绩的增长点,同时也有助于教学相长.通过这个实例可以发现,仅依靠一个统计图(表)进行分析成绩往往是不够精准的,因此,教学中需要帮助学生厘清不同统计图(表)的优势与不足,用统计图(表)对数据进行表达时做到有的放矢,培养学生能应用不同统计图(表)描述数据,为精准分析数据提供支持,发挥统计图(表)更大的价值.
4.2 善用数据“说话”,培养数据观念
4.2.1 遇到问题能想到“数据”
2016年12月,工信部正式印发了《大数据产业发展规划(2016—2020)》,规划指出数据是国家基础性战略资源,大数据将为新一轮科技革命和产业形态的发展提供机遇,是21世纪的“钻石矿”.2022版新课标前言部分指出,必须进一步明确“培养什么人、怎样培养人、为谁培养人”.当今世界科技进步日新月异,课程内容也必须与时俱进,教师的教学理念也需要不断更新迭代,数据观念的培养不能局限于课堂教学中,应该要渗透在学生的日常生活中.例如,笔者班级有学生提出数学考试时间不够用的烦恼,面对这样一个问题,部分学生就去盲目刷题,耗时耗力,效果也不理想,当学生在生活中遇到不能解决的问题时,教师可以引导学生积累一些数据去进行改进.比如记录每一次作业的所用时间,甚至可以记录每一次作业每一道题目的所用时间,找出是哪些类型的题目耗时较长,再去寻找改进策略,改进后继续跟踪解决同类型问题的耗时是否有所改善,应用学生真实面临的困惑为载体,逐步让学生想着用数据去解决日常生活中的问题,在解决问题过程中亲身经历数据的“收集、整理、描述、分析”过程,潜移默化培养数据观念.同样,教师遇见困惑后也应该尝试应用数据去寻找策略,例如上文案例中笔者应用不同的统计图对学生期末考试成绩进行分析,并尝试记录应用数据解决问题的感悟,这对培养学生的数据观念会更贴切,更能与时代接轨.换而言之,培养学生遇到问题时能想到应用“数据”进行研究,教师首先需要有这样的意识.
4.2.2 能分析数据,进行决策
《义务教育数学课程标准(2022年版)》中新增“理解中位数、众数的意义”,由此可见,统计量的含义得到足够的重视,打破了以往教学中“统计等同于数的运算”的现象,能根据统计量的含义看到数据背后的故事,这为人们研究微观世界提供了一种手段.近两年,根据数据的数字特征解释某一现象或进行决策的中考试题越来越多.例如2023年广东省中考试卷第21题,这道题目第1问要求学生找出平均数、中位数、众数,第2问要求学生应用你所学的统计知识,帮助小红分析如何选择乘车线路.此题的背景贴近实际,是学生生活中的常见问题,通过这样的问题能够从真正意义上考察学生的数据分析素养.与前两年中考统计试题相比,类似于这样的试题在2023年中考试题中大幅度增加.例如广西省中考试卷第21题、甘肃省白银市中考试卷第23题、内蒙古包头市中考试卷第19题、浙江省温州市中考试卷第19题等,感兴趣的读者可进行查阅.四分位数与箱线图是2022版新课标中新增的内容,各版本教材还没有更新,但是教师的教学理念应该顺应时代发展,建议教师在进行统计模块的教学时,依据2022版新课标的要求对该部分内容进行适当补充.
参考文献
[1]中华人名共和国教育部.义务教育数学课程标准(2022版)[M].北京:北京师范大学出版社,2022:74—75.
[2]杨帆,陈良强,罗汝叶,等.基于箱线图对大曲质量的判别分析[J].酿酒科技,2015(05):1-3.
[3]吳九牛,高德成,蒋维栋,等.基于箱线图的插值法在空盒气压表数据处理中的应用[J].工业仪表与自动化装置,2023(03):93-98.
[4]鲁俊,蔡亮.应用箱线图预测兰州市新生儿出生缺陷的发生率[J].甘肃科技,2018(24):20-22.
[5]宋乃庆,刘彩霞,陈婷.义务教育新课标“统计与概率”领域的发展变化——基于数据素养培养的视角[J].课程·教材·教法,2022(09):27-34.
[6]刘华明.初中数学统计与概率的新成员——四分位数与箱线图[J].中小学数学(初中版),2023(01):116-117.
[7]孙晓天,沈杰.义务教育课程标准(2022年版)课例式解读初中数学[M].北京:教育科学出版社,2022:86.
作者简介 高凯亮(1995—),男,贵州六盘水人,本科学历,中学二级教师,南京市江北新区初中数学工作坊核心成员;主要从事初中数学教学与研究,热衷于研究教师如何激发学生学习兴趣与深度思考的方法探究,并在实践中取得一定经验与成果;在数学专业期刊发表论文近20篇;荣获南京市江北新区第三届“教育科研成果创新奖”特等奖.
中学数学杂志(初中版)2023年5期
