分析学情 有序思考 提炼模型 提升素养
程峰 张林

【摘 要】 分析和调查学生在解答一道画图题时的困惑和思维盲点,有助于教师深入理解题目,挖掘题目,寻求适合学生解题思路和方法,并提炼出几何模型,在发展学生思维能力的同时训练了学生的几何直观能力、逻辑推理能力,从而提升学生的数学素养.
【关键词】 思维盲点;几何模型;问题本质
1 题目呈现
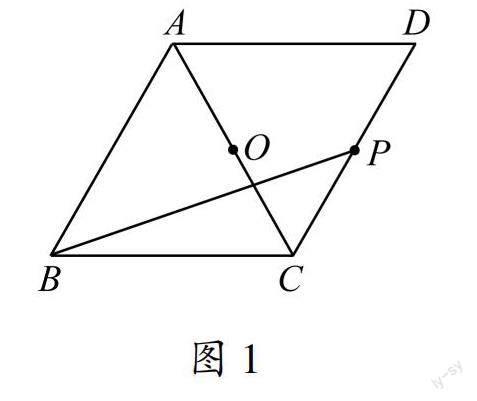
如图1,在菱形ABCD中,P是CD的中点,O是对角线AC的中点,∠A=120°,连接BP,请仅用无刻度的直尺按要求完成以下画图(不写画法,保留作图痕迹).
(1)在图1中画出BC的中点M.
(2)在图2中画出线段BP绕点O顺时针旋转60°后的图形.
本题是笔者所在学校一次模拟考试题.本题以常见的含120°(或60°)角的菱形为背景,图形简洁,主要考查旋转作图,考查图形结构的内在逻辑关系,对学生的数学素养要求较高.本题第(2)问得分率很低,不到20%(注:本文主要讨论第(2)问,第(1)问略),大部分学生不能确定B点旋转后的位置.有很多学生凭主观臆断,胡乱画出B点旋转后的位置,也有很多学生直接画出旋转后的线段,没有画图痕迹.
2 学情分析
在教学之前,笔者对学生的错误画法进行了分析,然后随机抽取不同层次的学生若干名,让他们谈谈在考试过程中对于此题遇到的困难或思维盲点.经过交流和分析,笔者发现学生的困惑和思维盲点主要集中在以下三个方面:
(1)无方向:这道题图形背景简洁,但简洁的同时,也给学生增加了难度,很多学生不知道往什么方向思考,毫无头绪.
(2)无图形:观察图形易知P点绕O点顺时针旋转60°到C点,△POC是等边三角形,根据旋转的性质,B点绕O点顺时针旋转后的对应点H,应是以OB为边的等边三角形的顶点,也就是画出另一个等边三角形,但是很多学生没想到.
(3)无思路:有学生虽然想到要画等边三角形,但是这个等边三角形如何画出?B点绕O点顺时针旋转后的位置如何确定?大部分学生找不到画图思路.
3 教学实施
3.1 分析图形特征,初步感知问题
如图3,为了有效寻找图形的内在逻辑结构,笔者提出问题:(1)菱形ABCD有什么特殊性质?如果连接OP,能确定△POC的形状么?(2)你能确定点P绕O点顺时针旋转60°后的位置吗?(3)你能确定点B绕O点顺时针旋转60°后的大概位置吗?
教学分析 通过分析图形特征,在问题串的解决过程中,学生自然发现和构造出符合要求的辅助线,通过思考与尝试,学生发现∠ACP=60°,且OP=OC,所以首先能确定P点绕O点顺时针旋转60°到C点,△POC是等边三角形,根据旋转的性质,B点绕O点顺时针旋转后的对应点H,应是以OB为边的等边三角形的顶点.
3.2 转化问题,寻求突破
问题 OH跟AB存在什么位置关系?
连接OB,由菱形的性质知∠AOB=90°,因此问题转化为在∠AOB内部画出以OB为边,点O为顶点的60°角,即∠BOH=60°,又易知∠ABO=30°,所以∠OGB=90°,也就是OH⊥AB,如圖4,这样问题又转化为过点O画线段OH⊥AB,垂足为点G.
3.3 继续探究,确定思路
问题:如何确定点G的位置呢?又如何确定点H的位置呢?
要画出垂线段OH,首先要确定点G的位置,猜想点G会是什么特殊点呢?如图5,延长PO交AB于点E,则E点是AB的中点,OA=OE,易知∠BOE=∠OBE=30°,所以∠EOG=60°-30°=30°=∠AOG,所以点G是AE的中点(三线合一),这样就确定了点G的位置.那么点H的位置又如何确定呢?如图6,延长DA,OG,它们的交点即为点H.连接HE,易证四边形OEHA,四边形OEBK都是菱形,且菱形OEHA≌菱形OEBK,OH,OB分别是它们对应的对角线,所以OH=OB,且∠BOH=60°,所以△OBH是等边三角形,即B点绕O点顺时针旋转60°得到点H.
教学分析 为了让学生充分理解如何寻找点B旋转后的位置,笔者将原问题分解成一连串相关问题,使学生从整体上把握问题的本质,获得解题思路.
3.4 画法生成,发展思维
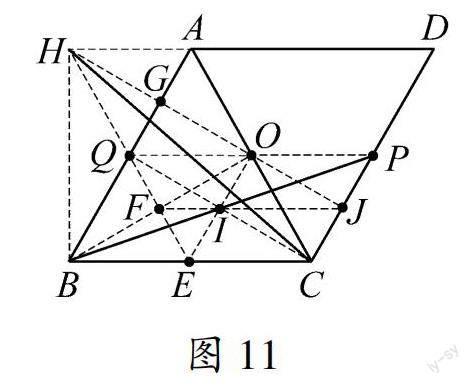
通过前面的思考和探究可知,只要画出AE的中点,就能画出B点旋转后的对应点,那么仅利用无刻度的直尺如何画出AE的中点呢?笔者放手让学生合作探究,课堂上得出了以下六种画法:如图7—12,各图中线段HC为线段BP绕O点顺时针旋转60°后的线段.
教学分析 通过循序渐进,抽丝剥茧的分析,最终得出只要画出AE的中点,就能画出B点旋转后的对应点.在整个思考和探究的过程中,使学生知其然,更知其所以然,较好地发散了学生的思维,训练了学生的几何直观能力,逻辑推理能力,从而提升了学生的数学素养.
3.5 提炼模型,理解本质
当旋转后的线段HC画出来后,笔者让学生回顾考试时遇到的困难和思维盲点,哪一步没想到?为什么没想到?是知识点遗忘还是方法不当?现在有哪些领悟?你能发现图7—12中都蕴含的一个模型图吗?如果发现了,把它画出来.当笔者把图7—12中部分线段隐藏起来,都只留下图13,学生纷纷感叹,原来就是特殊的“手拉手”模型图,原来此题就是把图13隐藏起来,让我们画出来即可.为了让学生进一步理解图13,笔者让学生尽可能的说出图13的性质:OP=OC,OB=OH,△OPC,△OBH都是等边三角形,△BOP≌△HOC,BP=HC,BP与HC的夹角是60°,线段HC是由线段BP绕点O顺时针旋转60°得到.笔者把这种画法形象地称为“手拉手模型法”,并提醒学生今后在遇到有关线段旋转的问题,首先可以考虑构造出“手拉手模型图”.
教学分析 笔者让学生进行反思,让学生明白“为什么这样画”“怎么想到要这样画”等问题,这需要教师引导学生对解题思路的认识不能仅停留在直觉层面,而要上升到理性层面.从画完后的图形中提炼出“手拉手”模型,既让学生发现问题的本质,又是思维上的一次升华.
3.6 运用模型,深化理解
为了进一步使学生理解和运用手拉手模型,笔者趁热打铁,提出以下几道变式问题:
(1)画出BP绕O点顺时针旋转120°的线段,如图14所示HK;(笔者提醒学生还是画等边三角么?)
(2)画出BP绕O点逆时针旋转60°的线段,如图15所示MH;
(3)画出BP绕C点顺时针旋转60°的线段,如图16所示AG;
(4)画出BP绕A点顺时针旋转60°的线段,如图17所示HF;
(5)画出BP绕D点顺时针旋转60°的线段,如图18所示MG.
教学分析 美国数学教育家G·波利亚曾说“好问题同某种蘑菇相像,它们都成堆地生长,找到一个以后,应当在周围找一找,很可能附近就有好几个”.因此,自然想到改变旋转中心或旋转角度对原问题进行变式探究,这样可以达到举一反三,触类旁通的效果,让学生再次感悟“变中有不变”,即问题变了而画法没变,仍然是构造“手拉手模型”.学生用已有的方法和经验解决新问题时,可以进一步感悟画图思路,提升解题能力,进一步理解、把握问题本质.
3.7 节外生枝,殊途同归
正当笔者要结束此题的教学时,一位画法正确的学生站起来说他的画法跟笔者讲的画法不同.该生的思路是把BP看作是平行四边形BCPG的对角线,因此先画出 图19BCPG绕点O顺时针旋转60°后的HFCA,连接对角线HC,则HC就是BP绕点O顺时针旋转60°后的线段.如图19所示.笔者表扬该生能在考试时间紧张的情况下想到旋转平行四边形的方法,体现了思维的灵活性、变通性,同时也体现了整体与部分的思想.当然,也可以看作是把△PGB(△PBC)旋转到△CAH(△CHF).从最后的画出的图形看,本质上还是“手拉手模型法”,用一个成语概括就是“殊途同归”.
4 教学反思
4.1 分析学情,保障教学有的放失
学生解题时的困惑和思维盲点从某种意义上说也是教学的起点.笔者在教学之前对学生试卷上出现的错误予以分析并与若干名不同层次的学生进行交流,通过6个教学环节,层层推进,有序展开,在破除学生心中疑惑的同时成功突破本题的难点,达到了学生知其然更知其所以然的教学效果[1].由此可見,只有建立在学生学情基础上的备课,才是有针对性的备课,才是理解学生的备课;只有建立在学生学情上的教学,才能保障教学活动有的放矢.
4.2 有序思考,促进思维能力提升
从本题的各种画法看,虽然最后画出的图形都是常见的手拉手模型,但是从学生的答题情况看,多数学生的思维障碍是难以确定旋转后的位置,无法与手拉手模型建立联系,无法将题中的条件进行整合,导致无法画出旋转后的图形.这就需要教师在教学时给予学生充分暴露思维的机会,在思维盲点处加以点拨.教师要引导学生有效审题,有序思考,由“已知”想“可知”,由“未知”想“需知”,找到中间环节,构建思维通道,寻找内在联系,从而理解问题的本质,最终实现学生思维能力的有效提升[2].
4.3 提炼模型,揭示问题本质
解题教学要注重对数学模型的提炼.在教学中,充分利用“数学模型”,将学生难以理解的知识进行适当的模型处理,以他们能够理解和接受的方式呈现出来,与他们的思维水平和已有的知识结构相融,学生就可以实现在最近发展区内对已有的知识的巩固,同时提炼模型也有利于学生更好地理解问题本质,揭示问题本质.
4.4 变式探究,落实素养提升
变式探究,一方面可以帮助学生巩固先前的所学知识和方法,另一方面可以拓展学生的视野,使学生更深刻地把握问题结构,理解问题本质.本节课几个变式问题,既达到了巩固练习的目的,又拓展了学生的思维;既培养了学生几何直观能力、逻辑推理能力,又落实了数学核心素养的提升.
参考文献
[1]郑金.贴近学情 提升能力 落实素养[J].中学数学教学参考(中旬)2022(8);32-34.
[2]徐一鸣.夯基础 长能力 促思考[J].中学数学教学参考(中旬)2019(4);45-47.
作者简介 程峰(1975—),男,中小学高级教师;主要研究初中数学教学.
张林(1985—),女,中小学一级教师;主要研究初中数学教学.
中学数学杂志(初中版)2023年5期
