基于平台力波动的压溃管结构参数优化设计

许平 ，关月溪 ，阳程星 ，魏鲁宁，杨雨晖，刘旭东

(1.中南大学 轨道交通安全教育部重点实验室，湖南 长沙 410075；2.中南大学 交通运输工程学院，湖南 长沙 410075；3.中车青岛四方车辆研究所有限公司，山东 青岛 266031)

车钩缓冲装置作为发生列车碰撞时最先变形的部分，其姿态和能量吸收性能将显著影响列车的动态行为响应[1]。因此，压溃管作为车钩缓冲装置的主要吸能元件，其参数配置和力学特性尤为重要。YAN 等[2]提出了考虑弯曲带来的剪切变形的理论分析模型。ABRI 等[3]基于运动学和平衡条件建立了描述厚壁固体管膨胀过程的解析和数值模型。LUO 等[4]通过研究得到了管壁径向挠度变化和所需驱动力随冲程变化的理论表达式，并估算了稳态下的最终半径和驱动力。SEIBI 等[5]对钢管和铝管进行了实验和数值研究，观察到膨胀管尖端出现回弹现象。朱涛等[6]梳理了近20年车钩缓冲装置在列车碰撞领域的研究方法和研究成果，阐述了车钩缓冲装置在列车碰撞中的作用，及其在车辆系统整体设计中的地位。STUART 等[7]通过仿真证明，在列车端部碰撞中钩缓装置的参数配置会影响列车的稳定。莫晓斌[8]建立了等效车钩模型，发现通过调整车钩缓冲装置的参数配置可以提高列车的耐撞性。吕锐娟[1]建立了弹性橡胶缓冲器和膨胀式压溃装置的有限元模型，并建立了四编组列车碰撞有限元模型，研究了碰撞速度、垂向高度差和横向偏移量对钩缓装置作用过程和运动姿态的影响。赵士忠等[9-10]对高速动车组中间车钩进行的碰撞实验表明，随着碰撞速度的提高，压溃管的阻抗力基本不变。罗玗琪[11]使用实体单元建立了压溃管的有限元模型，研究了诱导面锥角角度、外套筒壁厚与直径对压溃管压溃时力值峰值与均值影响。然而，大多数针对压溃管的研究主要集中在吸能特性和影响吸能响应的参数上，对于压溃管平台力波动的研究很少。压溃管是车钩缓冲装置中最重要的吸能元件，其平台力波动的幅度会影响车钩压溃时的平稳性。本文以某型车钩为试验对象，对压溃管进行建模，分析各项参数对比吸能、平台力、平台力波动的影响，并通过优化方法获得车钩耐撞性设计中膨胀管的最佳配置。

1 试验与有限元仿真

1.1 压溃式吸能结构

压溃管作为车钩的主吸能元件，是城市轨道车辆上的一种重要吸能结构，如图1所示。压溃式吸能结构由压溃管和加压管2部分组成。压溃管末端呈喇叭形，管长280 mm，与加压管的锥形部分配合良好。同时，在加压管上设置了一个止挡销，用以观察压溃时刻。表1 给出了压溃管的厚度T，内径R，加压管的锥角α和外半径r。压溃吸能结构的主要几何尺寸见表1。

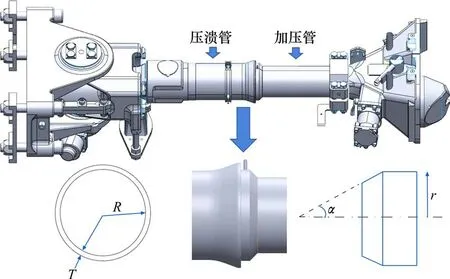
图1 压溃管结构形式Fig.1 Main structure of crushed pipe

1.2 试验测试

为了研究吸能结构的冲击特性，进行了碰撞试验，碰撞试验原理以及现场布置如图2 和图3 所示。在刚性墙一侧安装测力装置，并将对侧车钩钩头安装在测力面板上。在台车一侧安装车钩安装座，并在安装座上安装冲击侧车钩。同时在试验台上方和侧向布置了高速摄影，轨道下方布置速度传感器，二者在台车发生碰撞前同步触发。在一切准备就绪后，释放配重38.96 t 的台车，考虑到压溃管完全压溃所需的动能，将试验速度设计为4.65 m/s。撞击瞬间，测速仪记录的速度为4.647 m/s。

图2 试验原理图Fig.2 Schematic diagram of the test

图3 试验现场布置图Fig.3 Layout of test site

1.3 有限元模型

根据试验现场建立了车钩碰撞有限元模型和整车简化碰撞模型，如图4 所示。将冲击速度4.67 m/s 和质量38.96 t 加载至台车质心，台车带动车钩及防护工装前进撞向刚性墙。简化模型中为了减少运算时间对车钩进行了简化，将车钩钩头简化成一个平面，并省略了对侧车钩钩头。

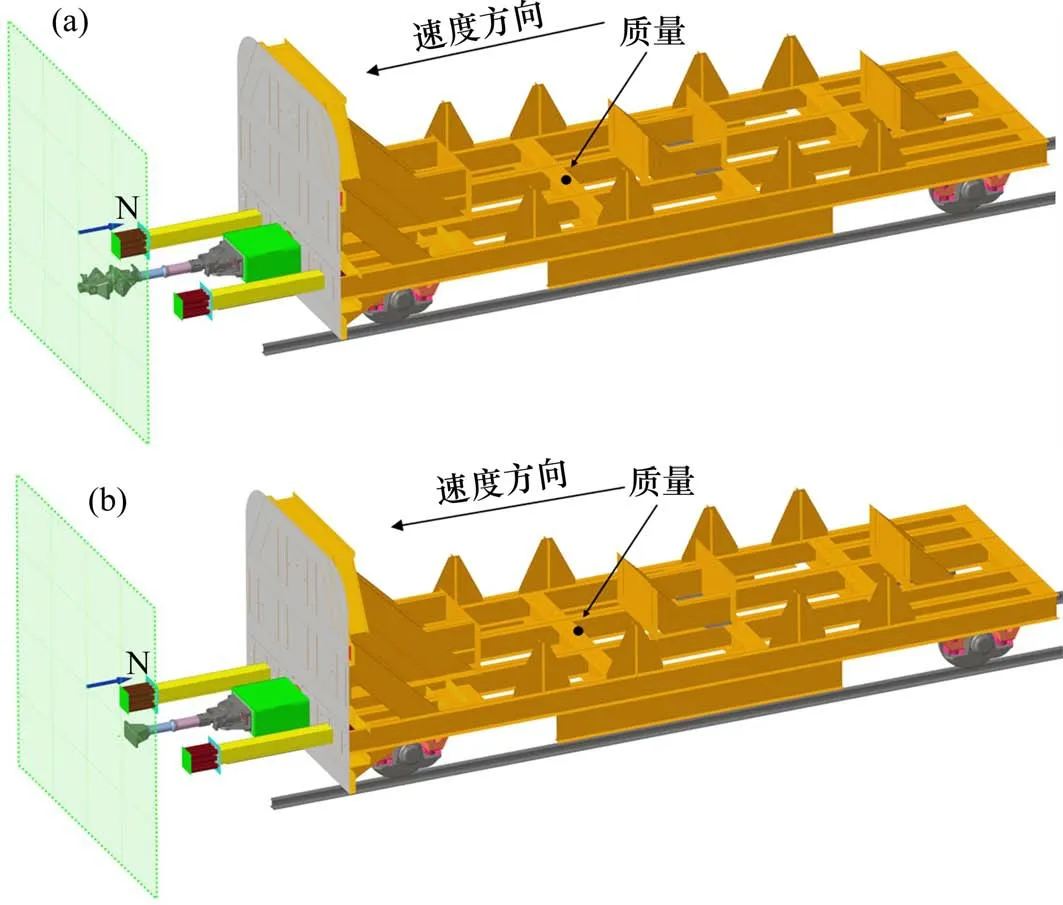
图4 整车碰撞模型和整车简化碰撞模型Fig.4 Vehicle collision model and vehicle simplified collision model

在模型的构建中，台车使用六面体实体网格建立并赋予LS-DYNA中刚性材料MAT RIGID。在碰撞过程中，除压溃管外其余元件变形较小，均使用刚性材料MAT RIGID，压溃管使用六面体实体网格建立，其余元件使用壳单元建立。各刚体之间的连接采用Constrained Rigid Bodies 进行连接。此外采用AUTOMATIC_SURFACE_TO_SURFACE 来设置压溃管与加压管之间的接触和轮轨之间的接触。采用AUTOMATIC_SINGLE_SURFACE 来设置压溃管的自接触，其中压溃管的静态和动态摩擦因数分别设置为0.36和0.14[1,12]。

通过仿真得到了整车模型和整车简化模型的力时间曲线，如图5所示。其中整车模型平台力为1 127.32 kN，整车简化模型的平台力为1 117.94 kN，两者相差0.84%，并且平台力波动幅度大致相同，可见车钩钩头并不会影响平台力的波动。

图5 力时间曲线对比Fig.5 Comparison of force time curves

为了便于后续优化，考虑将车钩及台车进行简化。车钩吸能主要是通过压溃管在压溃时膨胀变形吸能。除去压溃管外，其余结构变形不大，均视为刚体。简化后的有限元模型如图6所示。将压溃管置于刚性墙上，加压管与压溃管留有1 mm空隙，避免发生初始穿透。将试验台车的质量和速度加载在加压管底部，来模拟台车碰撞时携带的能量，即重量为38.96 t，速度为4.67 m/s。

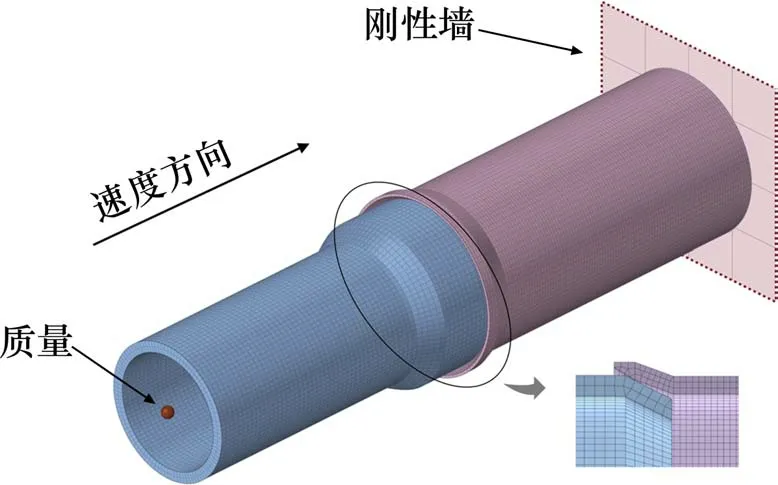
图6 简化仿真模型Fig.6 Simplified simulation model

将2个模型得到的力时间曲线进行对比，如图7 所示。2 条曲线在上升和稳定阶段趋势一致，且平台力波动幅度高度相同。整车模型平台力为1 117.94 kN，简化模型平台力为1 112.72 kN，相差0.54%。说明简化模型计算准确可靠，可用于后续研究，后文皆采用简化模型。

简化仿真模型采用6面体实体网格，通过沿变形管厚度方向增加单元数进行网格收敛分析，寻找最佳网格尺寸。结果表明，3 mm 的膨胀管单元尺寸能够保证准确的变形过程。详细的收敛过程如表2所示。

表2 网格尺寸对平台力、吸能量的影响Table 2 Influence of grid size on platform force and energy absorption

有限元模型采用了2种接触算法。采用自动面对面接触算法(AUTOMATIC_SURFACE_TO_SURFACE)来设置压溃管与加压管之间的接触。采用自动单表面接触算法(AUTOMATIC_SINGLE_SURFACE)来设置压溃管的自接触。2 种接触算法的静态和动态摩擦因数分别定义为0.36和0.14[1,12]。

压溃管材料采用LS-DYNA 材料库中的Mat Piecewise Linear Plastic，材料属性曲线是来自于压溃管材料拉伸试验的有效应力应变曲线，其屈服强度δy=406 MPa、杨氏模量E=206 GPa、泊松比γ=0.3。材料曲线如图8 所示。由于加压管在实际碰撞过程中变形较小，因此将其视为刚体，采用LS-DYNA 材料库中的MAT RIGID。其材料参数为杨氏模量E=206 GPa，泊松比γ=0.3。

图8 压溃管有效应力应变曲线Fig.8 Effective stress-strain curve of crushed pipe

1.4 有限元模型的验证

除需要进行简化外，有限元模型的建立均参照试验设定。为了验证有限元模型的准确性，对压溃过程中每一步的模拟结果和试验结果进行了比较。图9 为试验测试与仿真得到的力-时间曲线对比。可以看出，2 条曲线的平台力趋于一致，试验与仿真模拟的膨胀管都具有可控、有序的变形，在变形过程中径向膨胀，轴向缩短。压溃管在碰撞过程中最初开口朝外，随着加压管向前移动，管壁膨胀弯曲，使得压溃管开口逐渐朝内，最终包裹住加压管。图中试验曲线在0.08 s 后剧烈上升然后快速下降，这是由于压溃管完全压溃后触发了车钩过载保护装置，即拉断螺栓拉断，此后车钩脱落，载荷力迅速下降。因为本文的研究对象是车钩压溃时的平台力，所以在仿真模型中并没有体现这部分内容。

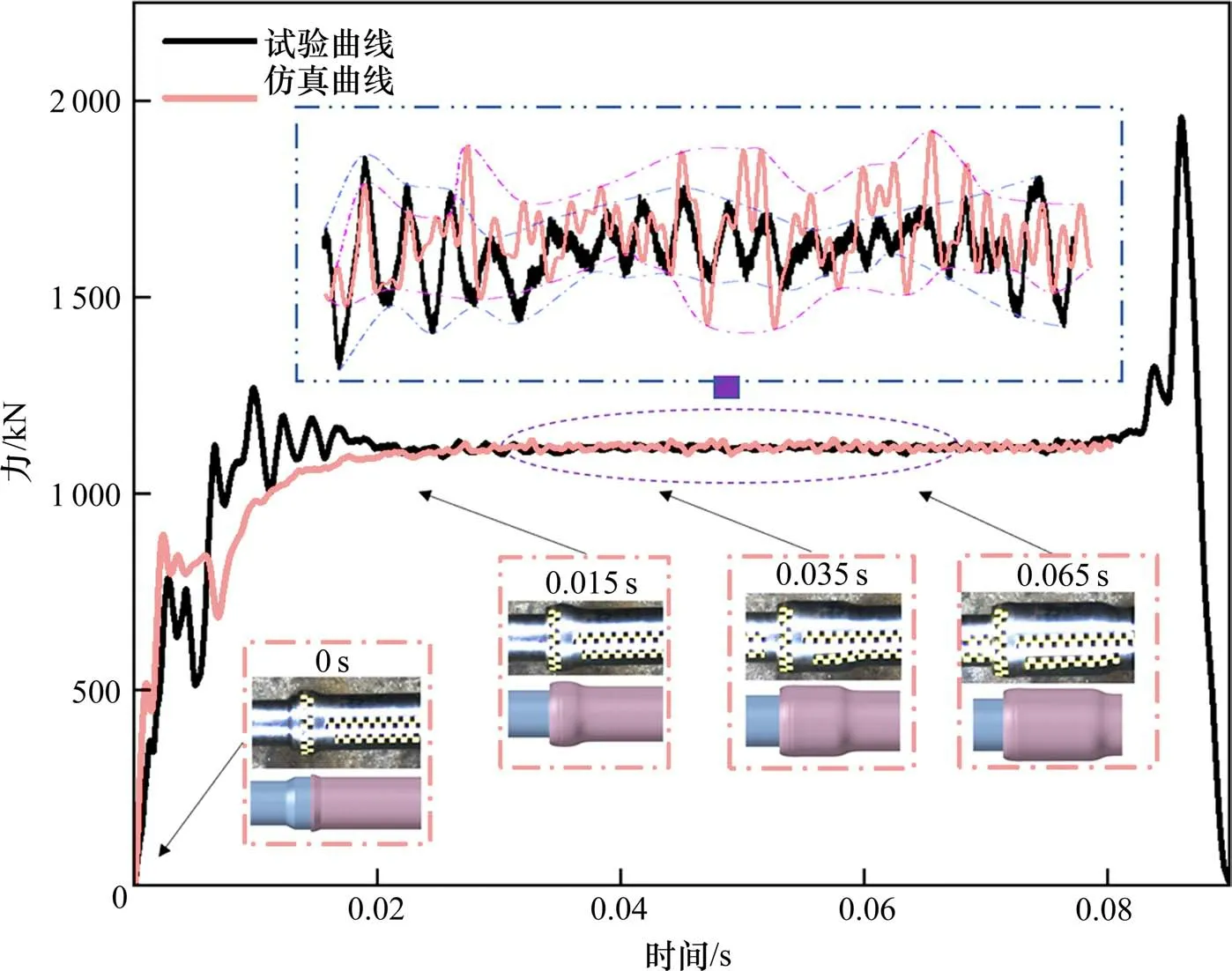
图9 试验曲线与仿真曲线对比Fig.9 Comparison between test curve and simulation curve

2 条曲线在上升过程中略有不同，仿真得到的力迅速上升后趋于稳定，而试验得到的力会快速上升到1 256.78 kN，然后趋于稳定。造成这种差异的原因是车钩在碰撞前会出现水平和竖直方向上的摆动。虽然采取了一定的固定措施，但由于试验条件复杂，仍不能保证不出现摆动角。

在整个过程中可以看到，仿真模拟和试验的力时间曲线吻合得很好。取0.03～0.065 s作为平台力的稳定时间段，期间仿真模型平台力波动最大值为1 137.32 kN，最小值为1 101.11 kN。试验测得的平台力波动最大值为1 137.00 kN，最小值为1 100.17 kN，两者波动幅度大致相同。仿真模型平均力为1 112.72 kN，试验测得的力值平均值为1 116.7 kN，两者相差0.40%，因此说明仿真模型精确可靠。

2 代理模型和影响因素分析

2.1 变量和响应

从能量守恒的角度来看，膨胀式吸能结构所吸收的能量主要通过压溃管的径向收缩、轴向膨胀和摩擦产生的热能耗散。因此压溃管的吸能能力与压溃管壁厚、加压管锥角、加压管外半径和摩擦因数有关。YAO 等[12]建立了膨胀式吸能结构模型，并对其结构参数进行了大范围变化的分析，在结果中指出压溃管厚度和加压管锥角分别是对平台力和比吸能影响最大的因素，摩擦因数次之。因此，在保持压溃管内半径不变的前提下，本文以压溃管厚度、加压管锥角和加压管外半径为变量。

结构参数优化的目的是建立稳定可控的变形模式。常用能量吸收(EA)、比吸能(Sea)和平均碰撞力(Favg)等指标来评价耐撞性[13-16]。除此之外，本文引入样本方差(S2)探究各因素对平台力波动的影响，这些指标见方程式(1)～(4)。

式中：φ代表F作用的距离，m代表整个物体的质量。样本方差越大代表平台力波动越剧烈，样本方差越小代表平台力越平稳。

2.2 试验设计(DOE)

DOE 被广泛应用于优化设计。可以将DOE 定义为一个测试或一系列测试，在这些测试中，对流程或系统的输入变量进行有目的更改，以便识别和观察输出响应中更改的原因。DOE 的研究目标是：1) 确定哪些因素对反应影响最大；2) 确定影响输入控制变量的设置位置，使响应接近期望的标称值，输出响应变异性小；3) 构建一个近似模型，该模型可作为计算密集型真实模型的替代模型。

试验设计过程中，比较常用的试验设计方法有部分因子法、中心复合法、全因子法、哈默斯利法和拉丁超立方法等，其中拉丁超立方体法可以将采样值在整个样本空间随机分布的同时，也可以保证采样值不过度聚集，即对于整个采样空间有较高的覆盖程度。本文采用拉丁超立方体法进行试验设计分析[17]。对压溃管厚度T，加压管锥角α，加压管外半径r进行200 次试验设计，产生200 个样本点。由于前文构建的仿真模型已经能较好地反应平台力波动，且过大的参数变动范围会使得压溃管发生不合理的变形模式，所以确定了如下的因素变化范围(见表3)。其中若只改变加压管外半径，则还会使得加压管角度发生改变。为了使各变量间互不影响，本文通过延长加压管锥角边长的方式改变加压管外半径，这种方式只会改变加压管外半径，并不会对车钩钩头安装半径和整体车钩结构造成影响。

表3 各因素变化范围Table 3 Variation range of each factor

2.3 主要影响因素

主要影响是一个自变量对响应的影响，忽略了任何其他自变量的影响。主要效果可以用线性效果的形式表示。线性效应使用线性回归模型计算，其设计变量范围为[0,1]。图10 展示了从DOE获得的线性效应形式的主要效应图。从主效应图可以看出，各因素对平台力、比吸能都是呈正相关的关系。对平台力波动而言，压溃管壁厚T，加压管锥角α是呈正相关的关系，而加压管外半径r对其是呈负相关的关系。此外压溃管厚度T对平台力影响最大，加压管外半径对比吸能影响最大，加压管外半径对平台力波动响最大。

图10 各因素主要效应图Fig.10 Main effect diagram of each factor

3 优化分析

3.1 优化问题的描述

在车钩膨胀式压溃吸能结构的设计中，为了获取最佳的结构参数配置，多目标优化设计被广泛应用。一般来说，越大的能量吸收能力越是轨道车辆所需要的。因此，将Sea 设置为优化目标，并将其最大化。该车钩安装在某型地铁车辆的前端，压溃管作为车钩的主吸能部件，在列车发生碰撞时发生作用，车钩中设有过载保护装置，当碰撞过程中载荷力过大时，会使得保护装置拉断车钩脱落。因此，压溃管的平台力并不是越大越好，应小于过载保护装置的拉断力并留有一定余量，避免在压溃过程中，提前触发过载保护装置，提前失效。该型车钩过载保护装置的拉断力为1 400 kN，故Favg 稳定在1 200 kN 较为合适。因此，将|Favg-1 200|设为优化目标，并将其最小化。在压溃过程中，平台力的波动也是我们关注的一个变量，过大的波动会严重影响整个车钩压溃的平稳性。在上文中，已经用平台力的样本方差来描述平台力的波动，因此将其设置为约束，样本方差的上限和下限分别设置为200 和0。将多目标优化用数学方法表示如下：

3.2 代理模型与误差分析

代理模型法是工业产品设计领域的一种替代方法，可以避免大量的仿真计算。该方法已被广泛应用于吸能结构的优化。对于压溃管的优化，已有许多学者利用上述方法进行了若干工作[13-15]，使压溃管的吸能能力最大化。本文通过拉丁超立方法生成200组数据点进行仿真分析，并使用哈默斯利方法生成了20 组数据点用于后续验证代理模型精度[16]。在构建代理模型时，考虑到本文中的压溃管的仿真会涉及到强非线性和大变形，径向基函数方法对解决这种强非线性问题有较好的适用性[16-17]。因此，选择采用径向基函数方法来构建代理模型。

径向基函数方法拟合的响应面模型如图11所示。

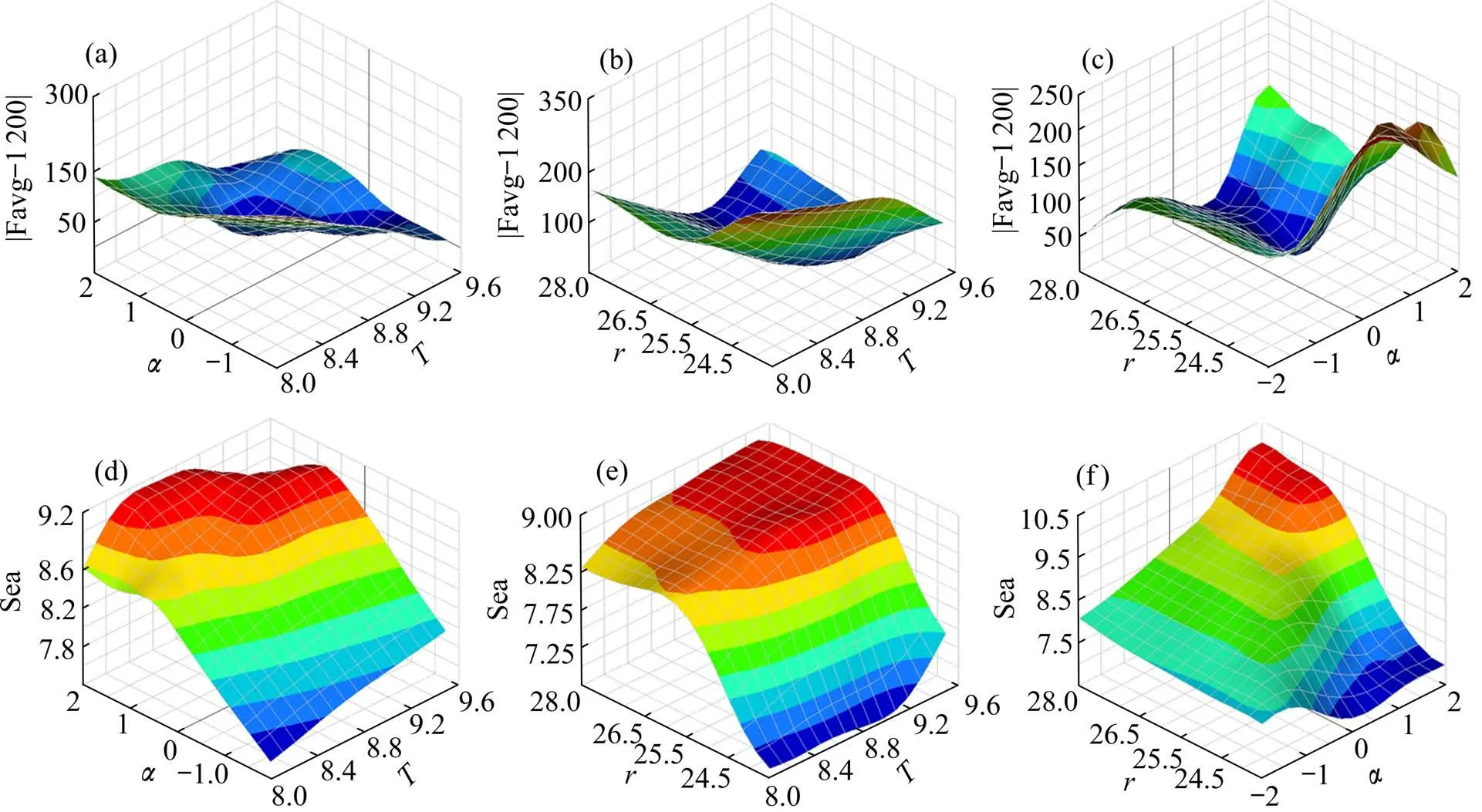
图11 响应面模型Fig.11 Response surface model

由图可知，对于|Favg-1 200|，随着2 个影响因素的增大，|Favg-1 200|都呈现先减小再增大趋势，其中r和α对其影响尤为明显，随着T的增大|Favg-1 200|逐渐减小。对于Sea，随着r，T和r，α的增大，Sea呈现逐渐增大的趋势，但在Sea达到8.6 kJ/kg附近时，r和T的增大对Sea增大的效果明显减小。而α和T的增大，使得Sea先增大后减小，而单独增大α或r，会使得Sea 后续增长缓慢。此外使用决定系数R2验证代理模型的准确性，其计算公式如下：

决定系数R2越接近1，则代理模型的预测精度越高，在此次拟合中|Favg-1 200|的R2=0.955 87,Sea 的R2=0.984 08。说明本文所构建的代理模型精度较高，可以用于后续优化。

3.3 优化算法

多目标遗传算法(MOGA)是利用遗传算法框架来解决多目标优化问题，与其他算法相比，具有运算速度快、解集收敛性好、Pareto 前沿分布均匀等特点[16]。近些年来许多研究者使用该方法研究仿真模型的结构参数优化。因此，本文采用MOGA算法来解决多目标优化问题，MOGA 的流程图如图12所示，相关参数设计见表4。

表4 MOGA算法参数Table 4 MOGA algorithm parameters

3.4 结果与讨论

压溃管多目标优化设计的Pareto 前沿如图13所示，随着Sea的增大，Favg与1 200 kN 的差距也在逐渐增大。为了得到平台力波动最小的参数配置，故选取Pareto最优解集中平台力波动最小的解作为最优解。

经过选取，确定了最优的加压管角度、压溃管厚度和加压管外半径，分别为28.68°，8.15°和26.46°。优化前后的对比如表5 所示，优化后的压溃管比吸能Sea 达到了9.72，相比于初始比吸能8.66 提高了12.16%，平台力波动由246.80 下降到102.48，下降了58.47%。优化前于优化后的对比见图14。

表5 压溃管性能优化前后对比Table 5 Comparison of crushed tube performance before and after optimization

由图14可知，优化后的平台力更加平稳，其在波动时最大值为1 212.98 kN，最小值为1 196.51 kN，且提高了比吸能，达到了优化目标。

4 结论

1) 在所有的设计变量中，加压管外半径对比吸能的影响最大，随着半径的增加比吸能逐渐增大，其次是加压管锥角、压溃管厚度，并且它们与比吸能也是正相关的关系。

2) 在所有的设计变量中压溃管厚度是对平台力影响最大的因素，其次是加压管半径，最后是加压管锥角。这3 个变量与平台力都是正相关的关系。

3) 在所有的设计变量中加压管外半径是对平台力波动影响最大的因素，其次是压溃管壁厚，最后是加压管锥角，其中压溃管外半径与平台力波动是负相关的关系，另外2个因素与平台力波动是正相关的关系。

4) 对于|Favg-1 200|，随着T的增大，|Favg-1 200|逐渐减小。对于Sea，在Sea 达到8.6 kJ/kg 附近时，r和T的增大对Sea 增大的效果明显减小。单独增大α或r，会使得Sea后续增长缓慢。

5) 与原方案相比，优化后使得车钩压溃管比吸能提高了12.16%，平台力提高了8.35%，平台力波动下降了58.47%，吸能量提高了6.34%。为提高车钩压溃平稳性，降低平台力波动提供了基于理论和工程参考。