潍莱铁路钢桁桥车桥耦合振动分析及行车安全性评估

张丛，孙洪斌，姜金凤，曹庆超，胡春建，朱志辉，余玉洁

(1.中铁十局集团有限公司 青岛分公司，山东 青岛 266000；2.山东铁路投资控股集团有限公司，山东 济南 250102；3.中南大学 土木工程学院，湖南 长沙 410075)

近年来，中国高速铁路得到了飞速发展，高速铁路桥梁也随之不断增多。钢桁梁桥具有建造速度快、结构刚度大和拼装方便等优点，被越来越广泛地应用于铁路桥梁[1-2]。为满足实际运输要求，高速铁路钢桁梁桥日益大型化、复杂化，桥梁的结构形式更加多样，受力状态也更加复杂[3-4]，因此研究铁路钢桁梁桥的动力特性，对确保钢桁梁桥动力可靠性和列车行车安全性有着重要的工程意义。在高速铁路建设中，冲击系数是铁路桥梁设计中考虑车辆动力效应的重要指标，影响着桥梁结构的安全性和经济性[5-6]。LIU 等[7]在车轮与桥面之间采用Hertz 弹簧建立轮轨之间的接触，运用半分离迭代的半解析方法研究了10 个自由度车辆的车桥相互作用问题。朱梦龙等[8]通过模型试验和软件模拟的方法，研究列车过桥时，桥梁跨中位置处的响应值随车速变化，以及车速和冲击系数之间的关系。陈敦等[9]利用ANSYS 和UM 动力学软件联合仿真，研究了铁路大跨简支钢桁梁车桥耦合振动的动力特性，并研究了车辆行车安全性指标。班玄耀[10]利用有限元软件对96 m 简支钢桁梁桥进行车桥耦合动力响应分析，研究了桥梁结构及桁架杆件不同参数动力响应。目前针对钢桁梁桥主要研究对象大多数为跨数较小的对称桁架桥，对于非对称大跨钢桁梁桥研究偏少[11-13]。因此为准确了解复杂结构的钢桁梁桥的动力特性，有必要对复杂钢桁梁桥进行车桥耦合动力分析和行车安全性评估。为研究非对称大跨钢桁梁桥动力特性，本文基于车桥耦合理论，结合潍莱铁路跨青荣特大桥进行车桥耦合动力分析和行车安全性评估，研究了桥梁主桁下弦节点挠度响应和主桁杆件应力响应，计算得出关键节点及杆件挠度和应力冲击系数，并分析了实际运营工况下桥梁行车安全性指标，为铁路钢桁梁桥设计及评估提供参考。

1 工程概况及有限元模型建立

1.1 工程概况

潍莱铁路跨青荣特大桥是一座位于新建潍坊至莱西铁路工程线的单线连续钢桁梁桥，桥梁全长203.6 m，计算跨度为120+82 m，设计行车速度为160 km/h。如图1 所示，桥梁为非对称钢桁梁桥，主桁采用竖杆三角桁，两端支座处的边桁高为13 m，中间支座处中桁高度为25 m，上、下弦杆均采用箱型截面，腹杆采用箱型截面或H 型截面[14]。上平纵联采用交叉式的腹杆体系，横撑及斜杆均采用工字型截面，与平联节点板的连接形式为对接熔透焊。桥面系采用正交异性钢桥面结构，钢桥面板与带节点的主桁下弦杆通长连接，共同承受主桁内力。钢桁梁桥的主桁杆件、整体节点、桥面系(横梁、横肋、U 肋)均采用Q370qENH 钢，填板、上平纵联、桥门架、横联及其拼接板等均采用Q345qDNH。桥面正线为60 kg/m钢轨，轨底至梁顶高660 mm，采用Ⅲ型混凝土轨枕，轨道类型为有砟轨道，单线桥面二期恒载重量按100 kN/m计。

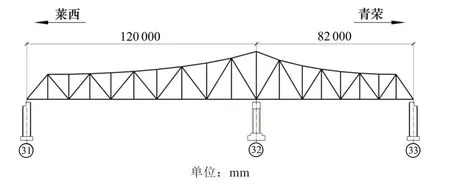
图1 潍莱铁路跨青荣特大桥立面图Fig.1 Elevation of Weilai Railway cross-Qingrong special bridge

1.2 有限元模型建立

采用有限元软件ANSYS 对桥梁进行全桥建模，有限元模型如图2所示，模型共建立14 776个节点，22 729个单元。为准确模拟车辆移动时桥梁的动力响应，在轨道两端各设置50 m 轨道延长段。在桥梁与轨道结构中，主桁、上平纵联、横联、钢轨、轨枕采用BEAM188 梁单元模拟，正交异性钢桥面板采用SHELL181板单元模拟，单元模拟参数见表1。钢轨与轨枕节点采用COMBIN14单元模拟扣件连接，轨枕节点与正交异性钢桥面板采用COMBIN14 单元连接模拟道砟的弹性支承，桥梁与桥墩采用COMBIN14单元模拟桥梁支座连接。

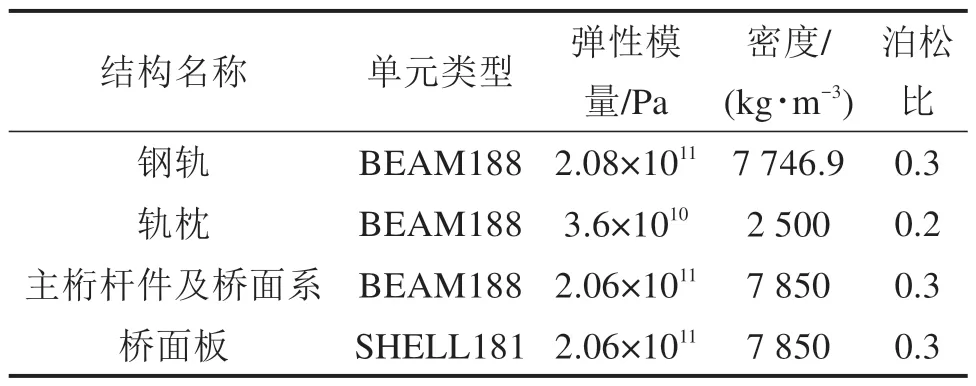
表1 单元模拟参数Table 1 Cell simulation parameters

2 潍莱铁路钢桁梁桥动力分析及冲击系数计算

2.1 潍莱铁路钢桁梁桥动力分析

通过对潍莱铁路钢桁梁桥在列车动荷载作用下的动力响应研究，得到主桁下弦节点的挠度变化时程和主桁杆件的应力变化时程，进一步研究了非对称钢桁梁桥的动力特性。为准确描述桥梁主桁下弦节点的位移和杆件的应力，对主桁下弦节点和杆件进行编号，见图3，主桁下弦节点编号为E0～E18，下弦杆编号为1～18，上弦杆编号为19～34，腹杆编号为35～69。

图3 主桁下弦节点和杆件编号Fig.3 Nodes and bar numbers of main joist lower chord

2.1.1 车桥耦合振动系统

车桥耦合振动系统对于准确分析桥梁动力响应有着重要的作用[15]。如图4 所示，每节车辆采用十自由度垂向车辆动力学模型[16]：mc，Jc分别表示车体质量和点头转动惯量；mt，Jt分别表示构架质量和点头转动惯量；mw表示轮对质量；k1，k2分别表示一系悬挂和二系悬挂的刚度；c1，c2分别表示一系悬挂和二系悬挂的阻尼；zcj，zb2j～zb1j，zw4j～zw(4j-3)分别表示车体、2个转向架和4个轮对的沉浮；θcj，θb2j～θb1j，θw4j～θw(4j-3)分别表示车体、2个转向架和4个轮对的点头。

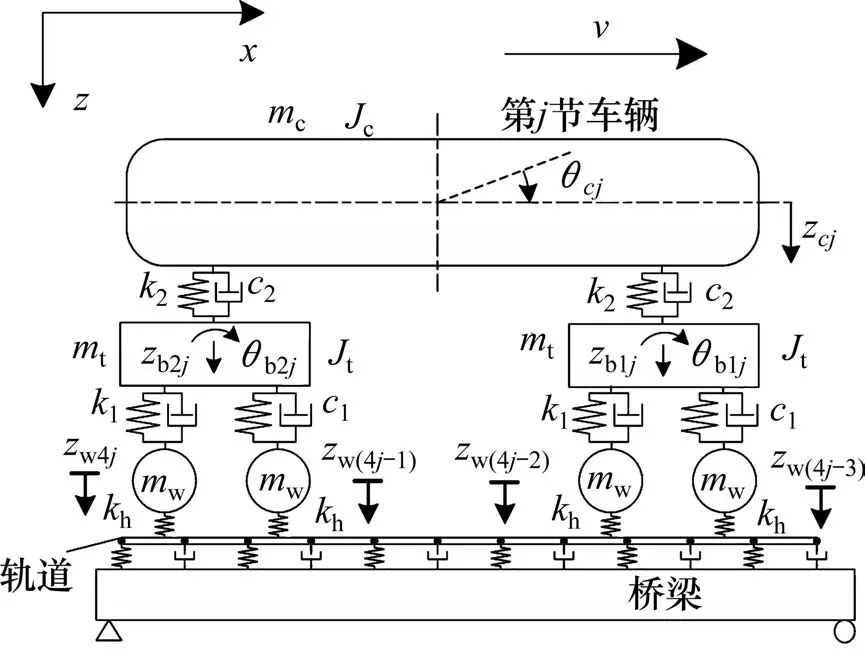
图4 车桥耦合系统Fig.4 Axle coupling system

车辆系统和轨道-桥梁系统之间通过轮轨接触相互作用，基于等效线性Hertz 接触模型模拟接触关系，车桥耦合振动方程如下：

式中：M,C,K为质量矩阵、阻尼矩阵和刚度矩阵；U,,为挠度向量、速度向量和加速度向量；Fvb,Fbv为车辆与桥梁的相互作用力向量；下角标v,b 分别表示车辆和桥梁；下角标vb,bv 表示车辆和桥梁之间的耦合作用。

车桥耦合振动方程式(1)中的矩阵和向量具体表达可参考文献[17]。通过使用Newmark-β 法对振动方程进行求解，求得桥梁单元动力响应。

2.1.2 桥梁主桁下弦节点挠度响应

结合桥梁实际运营情况，采用8 节CRH2 列车编组(2×(动车+拖车+拖车+动车))开展列车动荷载作用下的车桥耦合动力响应分析。考虑德国低干扰谱作为内部激励源，车辆以设计时速160 km 单线通过桥梁，得出桥梁主桁下弦节点的挠度响应时程和主桁杆件应力响应时程。为了研究桥梁动力冲击系数，通过施加同等大小移动静荷载得到静力过桥的桥梁响应，对比分析桥梁在车桥耦合作用下的动力特性。

图5为静力过桥和车桥耦合作用下的主桁下弦节点E5 和E14 挠度时程和各节点最大挠度计算结果。图5(a)和5(b)展现了桥梁左跨和右跨主桁下弦挠度值最大节点的挠度时程。从结果可知，桥梁主桁下弦节点E5 和E14 车桥耦合作用下应力时程曲线比静力过桥作用的应力时程曲线的幅值更大，说明车桥耦合作用对桥梁响应具有冲击效应。对比图5(c)中静力过桥和车桥耦合作用下主桁下弦各节点最大挠度，车桥耦合动力作用下节点挠度响应更加敏感，左跨下弦节点挠度最大值为9.604 mm，右跨下弦节点挠度最大值为3.583 mm。对比桥梁静力分析主桁下弦节点挠度，桥梁左跨挠度最大节点均为节点E5，右跨最大挠度节点在静力分析下为节点E15，在动力分析下为节点E14。

图5 主桁下弦节点挠度响应Fig.5 Deflection response of main truss lower chord node

2.1.3 桥梁主桁杆件应力响应

图6为静力过桥和车桥耦合作用下的桥梁主桁杆件应力时程和各杆件最大应力响应计算结果。图6(a)～6(c)给出了主桁各部分应力值最大杆件的应力时程。从结果可知，桥梁主桁下弦杆最大应力为4.237 MPa，位于1 号下弦杆，上弦杆最大应力为-9.04 MPa，位于21 号上弦杆，腹杆最大应力为10.725 MPa，位于47 号腹杆；主桁下弦杆主要以拉应力为主，靠近中支座附近杆件受压应力，主桁上弦杆在中支座附近杆件受拉应力，两端支座附近杆件均受压应力，相邻杆件应力相近。对比桥梁静力分析主桁杆件应力响应，主桁上弦杆应力最大杆件位置均为21号杆件，在静力分析下，主桁下弦杆应力最大杆件位置为3号杆件，主桁腹杆应力最大杆件位置为51 号杆件，在车桥耦合作用下，主桁下弦杆应力最大杆件位置为1 号杆件，主桁腹杆应力最大杆件位置为47 号杆件，动力分析与静力分析下，桥梁主桁最大应力位置存在差异。

2.2 潍莱铁路钢桁梁桥冲击系数

2.2.1 桥梁主桁下弦节点挠度冲击系数

当列车以一定速度通过桥梁时，桥梁产生振动，使得桥梁结构的振动挠度、振动应力比相同大小的静荷载作用时挠度和应力大，可用冲击系数μ来描述这种增大的影响程度，如式(2)所示。

式中：Rdyn为列车动力荷载作用下桥梁构件最大动力响应值，Rst为同等大小静力加载时的最大静力响应值。

我国《铁路桥涵设计规范》(TB 10002—2017)规定：高速铁路桥梁结构冲击系数与桥梁加载跨度有关，当桥梁加载跨度大于67 m 时，桥梁冲击系数(1+μ)均为1.0，μ值为0。

图7为桥梁主桁下弦节点挠度冲击系数计算结果。主桁下弦节点挠度冲击系数均小于0.04，节点挠度冲击系数最大值位于节点E15，桥梁主桁整体竖向刚度较大，所以竖向挠度冲击系数偏小。由于桥梁为非对称钢桁梁桥，桥梁刚度分布不均匀，中支座处主桁竖向刚度最大，因此节点E9-E11 处挠度冲击系数最小，右跨下弦节点挠度冲击系数变化较左跨更敏感。桥梁主桁下弦节点挠度冲击系数均大于规范限值，说明现有桥梁规范对冲击系数规定不适用于此大跨钢桁梁桥。

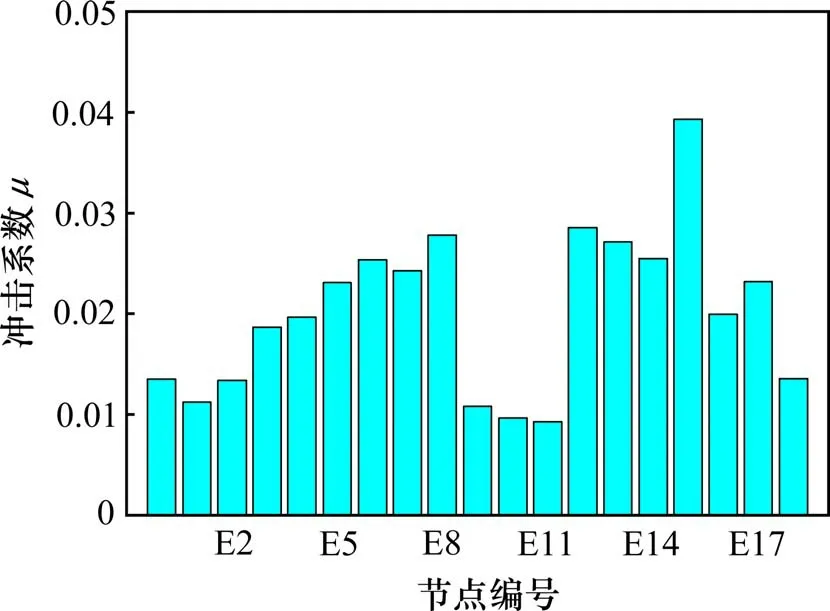
图7 主桁下弦节点挠度冲击系数Fig.7 Deflection impcct factor of main truss lower chord node

2.2.2 桥梁主桁杆件应力冲击系数

图8分别给出了桥梁主桁各部分杆件应力冲击系数的计算结果。从结果可以看出，桥梁主桁下弦杆应力冲击系数最大值为0.133，位于下弦杆7号，桥梁主桁上弦杆应力冲击系数最大值为0.039，位于上弦杆24 号，桥梁主桁腹杆应力冲击系数最大值为0.697，位于腹杆62 号；桥梁主桁各受力杆件应力冲击系数存在差异，其中腹杆的应力冲击系数最大，下弦杆应力冲击系数次之，上弦杆应力冲击系数最小，桥梁各杆件应力冲击系数均大于规范限值，因此在结构设计时应考虑必要的冲击系数放大，以保证桥梁安全。

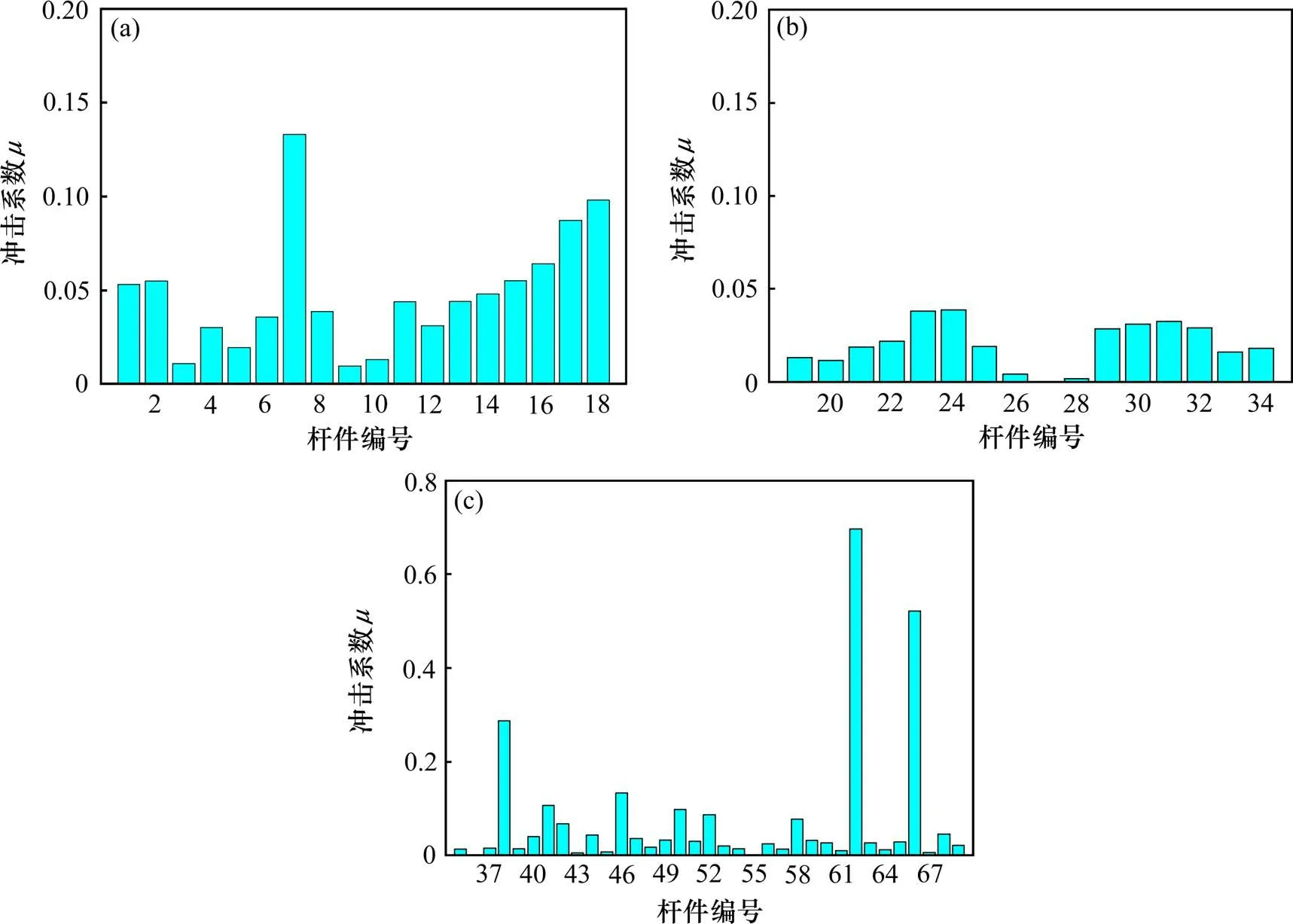
图8 主桁杆件应力冲击系数Fig.8 Stress impact factor of main truss rod

3 列车行车安全性

列车的行车安全性是保证列车能够安全行驶的重要指标。当车辆在线路上运行时可能受到多种荷载作用，在力的最不利组合情况下，可能会使轮轨分离，从而导致车辆脱轨或倾覆。现有列车运行安全性评估指标有列车脱轨系数Q/P，轮重减载率ΔP/P以及轮对横向力Q3 个指标，因此本文采用以上指标作为评估车辆运行安全性依据。TB 10621―2014《高速铁路设计规范》针对这些指标分别进行明确的规定：脱轨系数Q/P≤10+P/3，轮重减载率ΔP/P≤0.6，轮对横向力Q/P≤0.8。

使用桥梁设计运营工况进行列车行车安全性评估，采用8 节CRH2 列车编组，考虑德国低干扰谱作为内部激励，得到了列车的轮重减载率、脱轨系数和横向轮轨力计算结果，见图9。

由图9 可知，列车轮重减载率最大值为0.512，脱轨系数最大值为0.124，横向轮轨力最大值为9.04 kN，3项行车安全性指标均小于规范限值，可以保证桥梁实际行车安全。由图9(a)可以看出，轮重减载率与规范相差较小，原因是轮重减载率主要与轨道不平顺相关，分析采用德国地干扰谱做为内部激励，造成轮重减载量ΔP变大，轮重减载率ΔP/P0增大。

4 结论

1) 潍莱铁路钢桁梁桥在列车荷载作用下，桥梁主桁下弦节点挠度响应和主桁杆件应力响应均会增大，对桥梁结构产生冲击效应；桥梁主桁下弦节点挠度冲击系数均小于0.04，节点之间挠度冲击系数差异较小；桥梁主桁应力冲击系数最大值为0.697，主桁各部分应力冲击系数存在较大差异。

2) 现有规范对桥梁冲击系数规定和计算方法不适用所分析的大跨度异型铁路钢桁梁桥，并且没有考虑各部分构件实际冲击系数差异性，整体取值偏小。所以在桥梁设计时应该充分考虑冲击系数放大，以及各杆件冲击系数差异，以保证桥梁使用安全性。

3) 高速列车运营工况下脱轨系数、轮重减载率以及轮对横向力3项行车安全性指标均满足规范要求，表明该桥上实际行车具有足够安全性；列车荷载作用下的非对称钢桁梁桥具有良好的动力特性和行车安全性，可以满足桥梁实际使用需求，本文研究成果可为同类型铁路钢桁梁桥的设计与计算提供参考。