350 km/h及以上高速受电弓气动抬升力研究

宋诗扬，孔龙飞，韩通新

(1.中国铁道科学研究院 研究生部，北京 100081；2.中国铁道科学研究院集团有限公司 机车车辆研究所，北京 100081)

我国高速铁路发展迅速，多条实际运营线路均已达到350 km/h 速度级。按照国家加快实施创新驱动发展战略和《“十四五”铁路科技创新发展规划》部署，目前正在大力推进CR450 科技创新工程，研制时速达到400 km 的CR450 高速动车组。高速铁路提速研究中，高速受电弓气动抬升力是一个重要课题，对确保列车稳定受流、系统使用寿命以及铁路运营安全至关重要。气动抬升力过高会加剧高速受电弓滑板与接触线表面的磨损，降低使用寿命；气动抬升力过低导致列车受流不稳定，产生拉弧，严重时甚至引发供电中断事故。尤其对350 km/h 及以上速度级的高速动车组，由于气动抬升力随运行速度增长急剧上升，对列车运行影响越来越大，因此，研究高速受电弓气动抬升力具有重要理论意义和实际应用价值。在进行高速受电弓气动抬升力的仿真计算时，一个关键前提假设是流体的可压缩性。虽然所有流体都具有可压缩性，但在低马赫值条件下，忽略流体可压缩性可在不显著影响计算结果的情况下大幅减少计算成本。当马赫值大于0.3 阈值时，则应采用可压缩流Navier-Stokes 方程以获得更准确的计算结果[1]。目前，国内外关于高速受电弓气动特性文献多数基于不可压缩流。如李瑞平等[2]采用不可压缩Navier-Stokes 方程和k-ε湍流模型，对350 km/h高速受电弓的气动力进行仿真计算，发现弓头升力对气动抬升力的贡献量最大，其次是上框架和下臂杆升力。戴志远等[3]采用不可压缩Navier-Stokes 方程和SSTk-ω，研究了不同上下臂杆直径对380 km/h 高速受电弓气动抬升力的影响，指出开口运行工况上臂杆气动抬升力和受电弓气动抬升力都随着上臂杆直径增加而增大，随着下臂杆直径增大而减小，下臂杆直径对受电弓气动抬升力的影响较小。林泽峰等[4]基于不可压缩流和k-ε湍流模型，对高速受电弓所处的有限个结构位移状态下各部件的气动力进行仿真计算，提出受电弓气动抬升力的传递系数与其工作高度有关，在受电弓从初始工作高度1.5 m 抬升至1.6 m 的过程中，整弓气动抬升力值随升弓高度的增大而减小。杨康等[5]采用不可压缩Navier-Stokes方程和k-ε湍流模型，对高速受电弓的气动力进行仿真计算，指出受电弓的空气抬升力与速度的平方成正比，高速情况下空气抬升力使弓网接触压力大幅增加，弓网受流质量变差。辛恩承等[6]采用不可压缩Navier-Stokes 方程和湍流模型，分析不同运行条件下空气动力学特性对受电弓的影响，提出受电弓迎风面受到的压力值都要明显大于其他部位的压力值，同时受电弓在列车运行时产生的气动抬升力也会随着列车速度的增加而增大，从而影响弓网受流质量。韩斐等[7]基于不可压缩流模型对最高时速为350 km 的高速受电弓气动噪声进行仿真计算，指出高速列车受电弓引发的远场气动噪声主要是低频和中频噪声，并且噪声频谱具有明显的主频。黄凯莉等[8]采用不可压缩Navier-Stokes 方程和SSTk-ω湍流模型，分析研究高速受电弓气动噪声特性，发现350 km/h 高速受电弓顺向射流降噪效果显著，逆向射流降噪效果不明显。王洋洋等[9]基于不可压缩流，通过仿真分析结果研究350 km/h 高速受电弓气动噪声产生的机理，并在此基础上引入翼缘仿生结构对当前受电弓结构进行优化改进，认为优化后的受电弓适当地提高了受电弓的升力，可以减小跳网情况的发生，有助于受流稳定。郭璐等[10]采用不可压缩流，分析不同射流速度对湍动能、涡量、表面声功率级及远场噪声值的影响，得到了最优射速并验证了气动噪声计算方法的准确性。唐则男等[11]采用不可压缩Navier-Stokes 方程和k-ε湍流模型，建立高速列车纯空腔射流参数化模型，发现受电弓弓头升力系数不受射流影响，并且降噪效果优于纯空腔射流，整体最多可降噪6.2 dB。王东屏等[12]采用不可压缩Navier-Stokes 方程和k-ε湍流模型，对1 600 mm 和2 800 mm 升弓高度下受电弓不同时速的气动力进行仿真计算，指出受电弓在工作高度2 800 mm 时，仿真结果与风洞试验结果较为一致，误差保持在10%以内。丁杰等[13]采用不可压缩流和k-ε湍流模型，对比分析不同列车速度、运行方向和安装位置等条件下受电弓的气动力特性，提出受电弓检测装置单体的迎风面为正压，边线及背风面为负压，增大边线的倒圆角半径和调整平切面是优化左右设备外形流线型的途径。SHI 等[14]基于不可压缩流，对单臂高速受电弓表面偶极子声源分布及噪声辐射进行仿真计算，发现气动噪声主要是低频与中频噪声。DAI 等[15]采用不可压缩Navier-Stokes 方程和SSTk-ω湍流模型，对带挡板受电弓的气动上升力进行了数值研究，指出在闭口方向时，挡板的升力随着角度的增加而增加，而在开口方向时，挡板的升力随着角度的增加而减小。ZHANG 等[16]采用不可压缩Navier-Stokes 方程和SSTk-ω湍流模型，研究受电弓固定位置对高速列车气动特性的影响，发现受电弓固定位置对头车气动阻力影响不大，对尾车气动阻力影响较大，对头车、尾车和受电弓气动抬升力影响明显。WANG 等[17]基于不可压缩流，计算350 km/h 高速列车和受电弓的流场和气动噪声，指出受电弓的噪声主要集中在头部、底座和推杆周围，随着分析频率的增加，受电弓噪声源的强度越来越弱。TAN等[18]使用不可压缩流，对高速受电弓在对称平面上的流场和气动噪声进行了仿真计算，提出垂直于气流方向的臂杆对气流的扰动作用更为明显，产生的旋涡脱落范围更大，脱落涡主要分布在受电弓弓头、上下臂铰接处和底座。从上述分析可知，目前国内外高速受电弓气动特性的仿真多为基于不可压缩流的一种方法进行。由于350 km/h 的速度对应的马赫值接近0.3 阈值，在特定环境或工况下可能无法全面反映受电弓实际运行情况。此外，目前少有对400 km/h 速度级高速受电弓气动特性的研究。因此，本文采用可压缩流和不可压缩流2种方式进行仿真计算，通过对比仿真结果并辅以线路试验数据验证，旨在对400 km/h 速度级高速动车组受电弓气动抬升力计算提供技术指导，并提示现有350 km/h速度级高速受电弓气动抬升力的相关潜在风险。

1 仿真计算

1.1 仿真模型

通过计算流体力学软件ANSYS FLUENT 对受电弓进行仿真建模，并对受电弓三维模型进行网格划分。仿真建模时，考虑受电弓生产商提供的CAD 模型细节繁多，计算费用高但对仿真结果影响甚微，因此采用简化模型。简化受电弓驱动装置内部结构、底座绝缘支撑，及细小组件如螺栓、铆钉、电缆线等。保留受电弓主体结构如上、下臂杆、拉杆、底座、弓头等，如图1(a)所示。导流板建模基于实际导流板几何形状和安装方式，采用前滑板导流板后倾斜，后滑板导流板前倾斜，形成“八”字形状。为减少近壁效应的影响，计算区域设定为50 m×25 m×25 m。整体计算区域网格划分单位0.3 m，受电弓内部局部细化网格单位0.05 m，外部细化网格单位0.1 m，整体计算节点数量为297.4 万个，计算元素数量为213.2 万个，网格增长率设为1.2。受电弓网格划分如图1(b)所示。

图1 受电弓模型和网格划分Fig.1 Pantograph model &mesh

图2 计算区域及边界Fig.2 Computational domain and boundary

1.2 边界条件

计算区域入口设为速度入口(velocity inlet)边界条件，流体速度参数为350～420 km/h。出口处则设置为压力出口(pressure outlet)边界条件，其中静态压力值设定为0。计算域的顶部以及两侧采用对称边界条件进行约束。受电弓表面及计算域的底部设定为无滑移边界(non-slip wall)。

1.3 仿真计算方法

基于SSTk-ω模型，在不考虑流体可压缩性时，空气流场为稳态，密度设为1.225 kg/m3。仿真过程中，流体相对受电弓运行保持恒速，不考虑流体与受电弓之间的热传导，采用不可压缩Navier-Stokes方程。考虑流体可压缩效应时，仿真模拟时加入能量守恒方程描述流体的内能、动能和压力能在流动过程中的变化，采用可压缩Navier-Stokes方程。空气流体参数见表1。

表1 可压缩流体参数Table 1 Compressible flow parameters

1.4 计算结果

由表2 和表3 可知，使用2 种方法仿真得到的气动抬升力均与速度成正相关关系。使用可压缩流计算得到的气动抬升力在各速度级条件下均小于使用不可压缩流方法。

表2 仿真计算结果(不可压缩流)Table 2 Simulation results (incompressible flow)

表3 仿真计算结果(可压缩流)Table 3 Simulation results (compressible flow)

如图3 所示，在不同运行速度和运行方向时，使用不可压缩流仿真得到的气动抬升力波动幅度均小于可压缩流结果。这是由于在不可压缩流假设下，密度变化被忽略。而在实际运行中，流体速度、压力和密度的波动都会导致气动抬升力变化。尤其当马赫数超过0.3 时，上述差异更为显著。此外，随着受电弓运行速度升高，气动抬升力波动幅度呈现上升趋势，在闭口方向运行时，气动抬升力均值和波动幅度都高于开口方向运行。

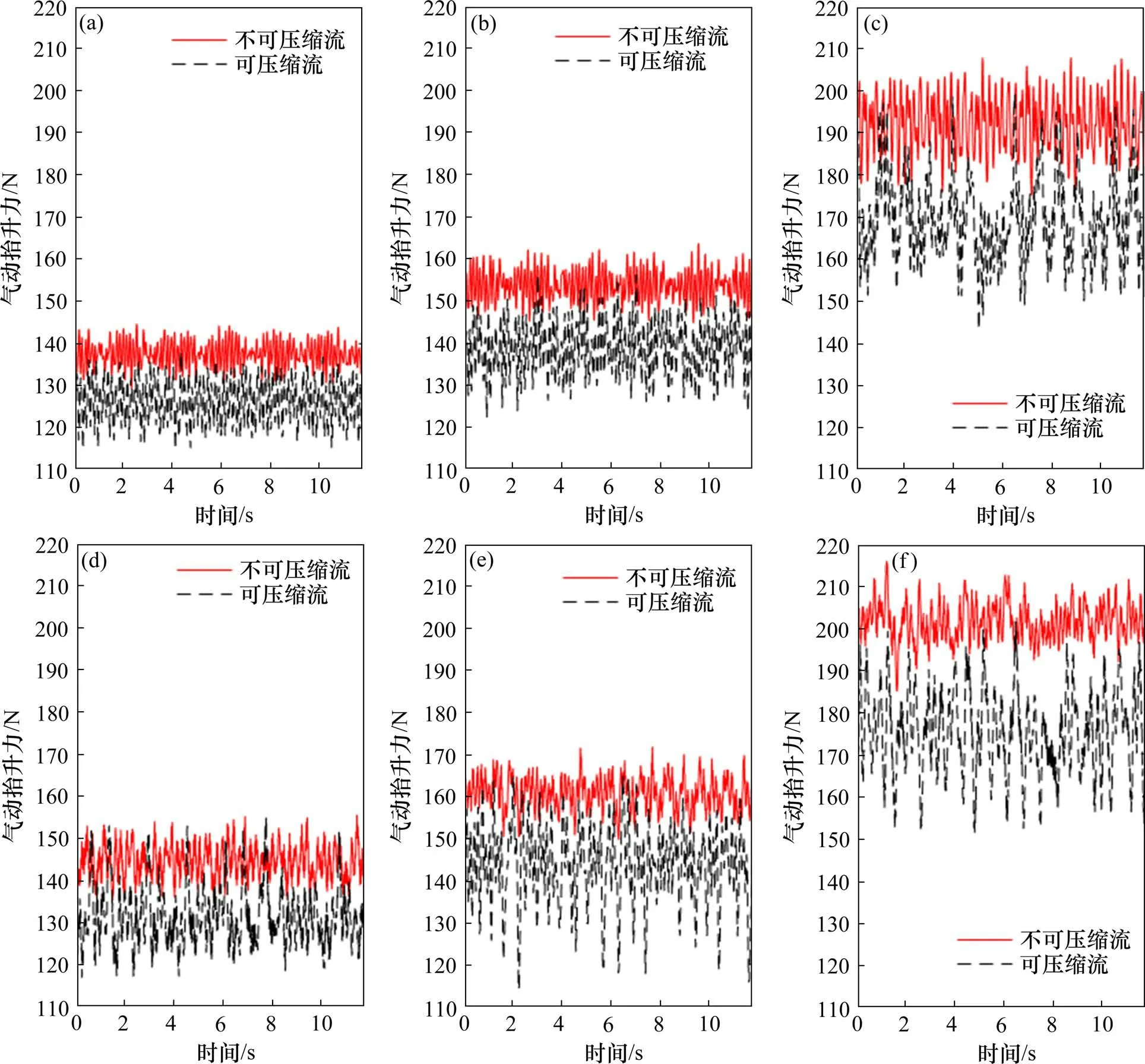
图3 气动抬升力仿真时程曲线Fig.3 Simulated time history curves for aerodynamic lift force

2 试验验证

2.1 工况信息

使用时速350 km 速度等级线路接触网，通过试验列车CRH380A-6041L 高速动车组对京沪先导段进行弓网受流性能综合测试。测试当天晴，无风，气温20 ℃。

2.1.1 接触线参数

京沪先导段上下行线路接触网采用不同试验区段设计，除各试验区段接触网的张力组合及采用的接触线材质不同外，其他主要技术参数相同，主要参数如下。

1) 接触网悬挂型式：高速正线采用全补偿式弹性链悬挂。

2) 接触网结构高度：高速正线为1 600 mm，隧道内、联络线、动车段线等为1 400 mm。

3) 拉出值：直线区段为 ±200 mm。

4) 锚段长度：高速正线不大于1 300 m，其余线路不大于1 600 m。

5) 锚段关节：采用四跨型式，但转换跨距不小于45 m。

6) 接触网电分相采用六跨两端口分相关节。

7) 高速正线区间，中心锚结采用防断的两跨式结构，站场设置防串中心锚结。

8) 高速正线接触网按采用棘轮补偿方式。

9) 接触网单腕臂柱采用热浸镀锌H型钢柱

10) 支柱高度：路基地段为7.8 m，合架供电线区段为11 m。

11) 路基区段不大于55 m，桥梁、隧道区段不大于50 m，转换跨距为50 m，相邻跨距之差不大于10 m。

2.1.2 受电弓参数

试验中使用的受电弓参数如表4所示。

表4 受电弓参数Table 4 Pantograph parameters

2.2 测量方法

试验前，在受电弓弓头安装4个压力传感器和4 个加速度传感器，分别位于2 个滑板两端的支座处(见图4(a))。其中压力传感器(图4(b))采用电阻应变式压力传感器，用于测量动态接触压力；加速度传感器(图4(c))考虑抗干扰性和过载容量，采用电容式加速度传感器，用于测量硬点冲击加速度。接触压力和加速度信号经屏蔽电缆传输至安装在受电弓底座平台上的高压侧信号处理箱，经放大、滤波、整形和V/F变换，变成适合光纤传输的频率信号，再经过光信号发射机和光缆传送至测试车内的低压侧，低压侧设有光信号接收机，F/V 变换器和整形电路将所有传感器信号复原，再送至数据采集和处理系统。

图4 试验设备及安装位置Fig.4 Equipment for the experiment and its installation location

数据采集和处理系统将采集接触压力和加速度数据用以下方式实时计算气动抬升力，并在显示器输出、保存：总接触力等于静态接触力、硬点冲击力和气动抬升力之和。其中，总接触力为前后滑板测量所得的接触力之和，静态接触力设置为70 N，硬点冲击力可根据牛顿第二定律计算，即质量乘以加速度(每根滑板两端的加速度测量的平均值减去重力系数9.8 m/s2)。气动抬升力可由总接触力减去静态接触力和硬点冲击力计算得出。

此外，车顶安装火花传感器、导高红外传感器和高速摄像机等，分别用于检测和记录燃弧、导高和受电弓运行状态。试验时，列车从静止状态加速至目标速度(350，380 和420 km/h)，上述所有传感器和摄像机从受电弓静止开始持续测量全程数据。图5为350 km/h试验时高速摄像机捕捉的视频截图。

图5 试验视频截图Fig.5 Screenshots of the video recording for the experiment

2.3 结果验证

分别以表2中350，380和420 km/h这3个速度级进行弓网受流性能综合测试，接触力及各相关结果如表5 所示。试验过程弓网接触力变化平稳，接触力标准偏差小，无接触网硬点和高差超限，弓网燃弧较小，无拉弧现象发生，燃弧率均少于5%，满足现行标准要求。动车组以最大速度420 km/h运行时，接触网最大抬升量为87 mm。

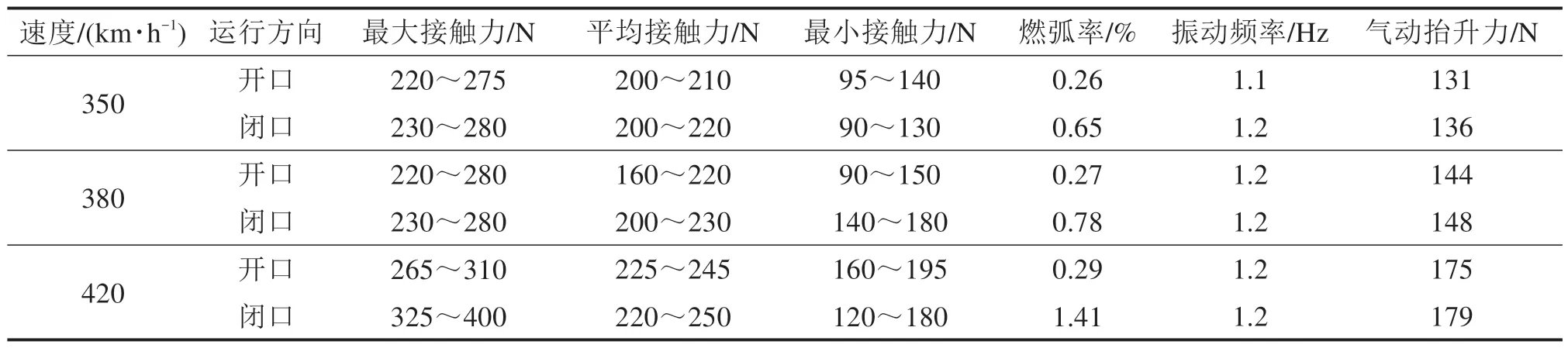
表5 测试结果Table 5 Measurement data

由图6可见，经对比测试结果，使用可压缩流方法仿真结果在不同速度级运行工况下结果更为准确，偏差较为稳定，约在2%～3%之间。使用不可压缩流方法偏差较大，并随速度显著增长，在420 km/h速度级偏差约10%(开口方向)和13%(闭口方向)。

图6 仿真结果和试验结果对比Fig.6 Comparison of simulation and experimental outcomes

3 结果分析

由上文可见，使用可压缩流方法仿真结果在不同速度级下更为准确。为进一步深入对前文结果的分析和讨论不同工况、运行环境下的气动抬升力变化，本节采用2种仿真方法模拟高速受电弓气动特性的压力分布及在特殊工况和狭窄环境中气动抬升力的变化。

3.1 压力分布

由图7可见，不可压缩流仿真中，受电弓前滑板和下臂杆处压力分布出现明显分层。该现象为边界层分离导致，即边界层从受电弓表面脱离，随后形成尾流。边界层在逆压梯度作用下导致边界层内部的动能减小，最终使边界层从受电弓表面分离。在分离区域，逆向流动的存在导致气流涡旋生成，从而使前滑板相较于后滑板的压力部分增加。而可压缩流仿真中压力分布更为均匀且符合实际情况。

图7 压力分布对比(10层边界层)Fig.7 Comparison of pressure contour (10 boundary layers)

如图8所示，通过增加边界层数量，可一定程度上改善压力分布在边界层的分离现象，分离层区域减少。在可压缩流仿真中，即使在层数划分数量较低的情况下，依然可以更为准确地描述高速受电弓压力分布。2 种仿真中，增加边界层数量均提高仿真压力分布结果准确性。

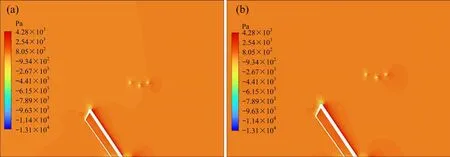
图8 不同分界层的压力场分布对比(25层边界层)Fig.8 Comparison of pressure contour (25 boundary layers)

因此，使用可压缩流仿真得到的压力分布区能更好地揭示受电弓流体动力学特性和压力分布规律，有助于理解高速受电弓气动抬升力的物理机制。

3.2 特殊工况环境

气动抬升力是空气分子作用在受电弓表面的机械力。考虑流体可压缩性影响即考虑流体密度变化带来的影响。温度、海拔等因素直接影响流体的密度和受电弓附件的局部声速。受电弓运行速度对应的马赫值是速度与局部声速的比值。在低温、高海拔、空气稀薄的特殊工况环境中，声速降低，对应的马赫值增高。例如，350 km/h速度级的高速受电弓在本文试验工况条件下，马赫值小于0.3，但在-25 ℃环境下，局部声速为315.77 m/s，对应的马赫值为0.31，需考虑流体可压缩性效应。

本文以温度因素为例，通过改变仿真中的温度参数，重复仿真。由图9可见，考虑流体可压缩性效应时，高速受电弓气动抬升力随温度下降显著上升；而不考虑流体可压缩性时，气动抬升力保持不变。这是因为不可压缩流仿真中忽略了温度影响下的流体密度变化。因此，可压缩流方法同样具有较高的适用性和准确性。由于我国铁路运营环境复杂多样，即使对于350 km/h 速度级的高速受电弓气动抬升力仿真中，也建议考虑流体可压缩性效应，以提高计算结果准确性。

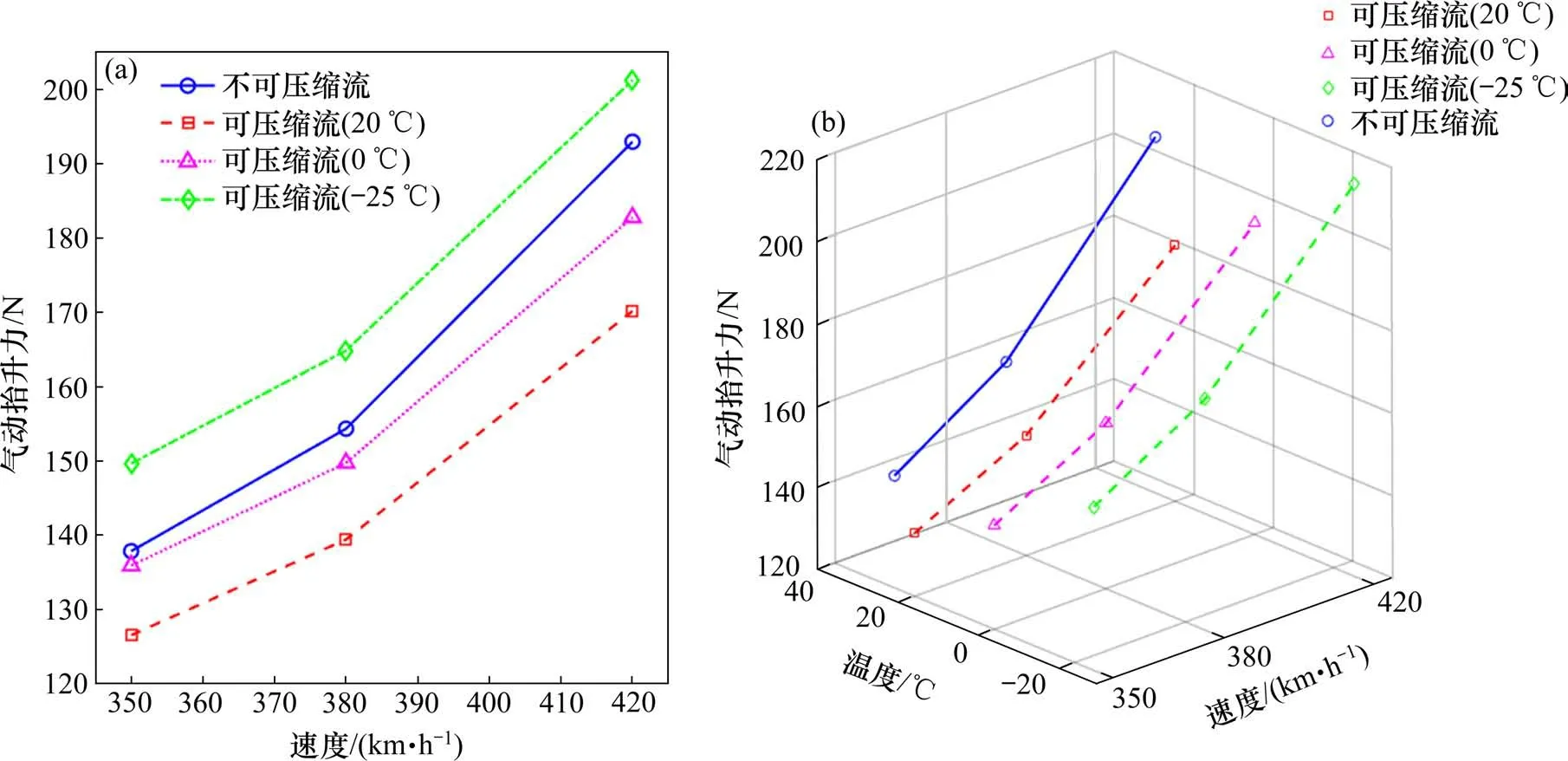
图9 开口方向和不同温度下2种方式仿真结果Fig.9 Simulation results with two methods under various temperature when running in the knuckle-upstream direction

依据《高速铁路工程动态验收技术规范》(TB 10761—2013)，弓网动态接触力评价一般按一个跨距为一个评价单位，评价参数有最大值、最小值、平均值和标准偏差，如下所示。

最大值：Fmax≤Fm+3σ；最小值：Fmin≥20；平均值：Fm≤0.000 97v2+70，式中v为速度；标准偏差：σ≤0.3×Fm。

在低温、高海拔、空气稀薄地区，高速受电弓理论气动抬升力随密度的降低而上升。为满足现行标准要求，应采取优化受电弓结构，调整运行参数(如静态抬升力等)，采用主动控制策略等方式来降低流体密度变化造成的额外气动抬升力。

3.3 狭窄环境

受电弓在隧道、山谷、车站等狭窄环境中运营时，在靠近隧道墙壁的区域，流体速度减小，压力梯度增加，同时湍流产生和消散的过程受到影响，产生壁面边界效应。流体在临近接触到隧道墙壁前，流体流动受到黏性力的主导，形成一个边界层薄层。边界层内，流体速度从0(壁面处)迅速增加至外部流动的速度，形成近壁区域效应。由于隧道内的流速变化，导致流体的可压缩性效应增加。

通过缩减计算区域横截面面积，以模拟高速受电弓在隧道内和其他狭窄环境中运行时受到的气动抬升力。如图10 所示，壁面横截面积越小，使用不可压缩流造成的偏差越大。高速铁路横截面积限值为100 m2，2 种仿真结果由于壁面边界效应和近壁区域效应造成的额外偏差最大为17%。此外，2 种仿真结果均表明狭窄环境内，高速受电弓受到气动抬升力增加。因此，在狭窄运营环境中，应考虑气动抬升力变化，通过合理措施和策略降低受电弓滑板与接触线由于接触力升高造成的磨损，延长系统寿命。

图10 不同横截面积、不同速度级下的开口方向运行仿真结果Fig.10 Simulation results with various cross sectional area and operating speed when running in the knuckle-upstream direction

4 结论

1) 对于400 km/h 及以上的高速动车组，建议使用可压缩流仿真计算方法进行受电弓气动抬升力分析，以获得更准确的预测结果。

2) 对于现有350 km/h 的高速动车组，在特殊工况和狭窄环境下，由于气动抬升力急剧上升可能引发的潜在风险，建议采取优化受电弓结构、调整运行参数等措施，降低气动抬升力，以提高运行安全和稳定性。同时，在设计和优化高速铁路线路时，应充分考虑特殊工况和狭窄环境的影响，以确保整个铁路系统的安全和高效运营。

本文研究成果不仅有助于推动高速铁路技术的创新和发展，还对提高高速铁路系统在特殊工况和狭窄环境下的稳定性和安全性具有重要意义。通过深入研究高速受电弓气动抬升力的相关问题，可进一步优化高速铁路运营技术，为高速铁路持续发展提供理论基础。