400 km/h高铁隧道组合型式缓冲结构泄压孔优化

杨伟超 ，李国志，何洪，刘义康，邓锷，罗禄森

(1.中南大学 土木工程学院，湖南 长沙 410075；2.高速铁路建造技术国家工程研究中心，湖南 长沙 410075；3.香港理工大学 土木与环境工程系，香港 九龙 999077；4.中铁二院工程集团责任有限公司，四川 成都 610031)

隧道洞口的微气压波严重影响附近居民生活质量，甚至导致洞口周围建筑振动，损坏洞口附近建筑结构[1-2]。目前，我国已有多条在建或建成高速铁路设计时速达到400 km。随着列车速度的提高，微气压波产生的负面效应愈发严重[3]。相关研究及工程实践证明[4]，单一型式缓冲结构的缓冲效果有限，等截面扩大+斜切+泄压孔的组合型式缓冲结构具有优良的缓冲性能。此前，刘堂红等[5-8]通过采用理论计算、数值模拟和动模型试验等手段，对不同缓冲结构型式展开研究，例如断面扩大无开口型和线性喇叭型缓冲结构、隧道洞门倾斜入口和帽檐斜切式洞门，研究表明缓冲结构型式对缓解效果有着显著的影响。同时，有部分学者针对缓冲结构的泄压孔也做了相关研究。例如，WANG 等[9]采用理论计算方法分析了泄压孔数量、尺寸和位置分布等因素对微气压波的影响规律，发现泄压孔面积对微气压波的影响效果最显著。TOKUZO 等[10]基于动模型试验和理论公式，以隧道内压力梯度峰值为优化目标，对缓冲结构的泄压孔进行了优化，发现压力梯度峰值与开孔面积呈线性关系。但以上学者仅针对单一型式的缓冲结构展开研究，且列车时速绝大多数为350 km 以下，在面对车速为400 km/h 时产生的微气压波，单一型式的缓冲结构难以满足规范要求[11]。一些学者注意到该问题并针对缓冲结构做了初步优化，提出了一些新型缓冲结构。例如，KIM等[12]基于动模型试验和生物仿真，提出类似于鲨鱼鳃的缓冲结构，发现采用新型缓冲结构时，隧道内初始压缩波和微气压波的峰值分别降低了56.3%和78.7%。ZHANG 等[13]通过1︰20 动模型试验，分析不同缓冲结构条件下隧道内瞬变压力和微气压波的变化特性，发现帽檐斜切式与泄压孔相结合的缓冲结构型式对微气压波的缓解效果最好。王英学等[14]通过数值模拟、模型试验和现场实测结合的方法，对比了采用间缝式开口和顶部开口缓冲结构的气动特性，发现间缝式缓冲结构缓解微气压波的效率及经济性更好。尽管国内外学者对各种型式的缓冲结构进行了积极的探索，但对等截面扩大+斜切+泄压孔的组合型式缓冲结构研究相对较少。考虑到列车编组、列车速度、地形地势、周围环境等因素的影响，不同场景下微气压波的实际控制标准不尽相同。为了使等截面扩大+斜切+泄压孔的组合型式缓冲结构满足更多实际场景的要求，有必要针对其几何参数进行进一步优化。本研究基于FLUENT软件的RNGk-ε双方程湍流模型，建立隧道-列车-空气气动仿真计算模型，通过现场实测验证数值模拟的正确性，从组合型式缓冲结构的泄压孔边缘到帽檐距离、开孔率、开孔数量及环向开孔位置4个方面展开研究，分析隧道内的初始压缩波和隧道洞口的微气压波，并提出等截面扩大+帽檐斜切+泄压孔的组合型式缓冲结构的最佳优化参数，为后续相关研究提供方向。

1 模型概述

1.1 几何模型

以设计时速为400 km 的双线隧道为研究对象，建立隧道-列车-空气气动仿真计算模型，如图1所示。隧道如图1(a)所示，其断面面积为100 m2，长度为1 000 m。列车采用2 编组，全长51.42 m，车头长6.12 m，外形光滑，建模时保持其基本流线特征。缓冲结构的断面面积为Sh=180 cm2，长度为60 m，宽度为18.5 m，厚度为0.5 m，其中帽檐斜切段长度为20 m，坡度i=1︰1.75，等截面扩大段长度为40 m。泄压孔间距取4 m[15-16]，宽度为4 m，泄压孔个数、长度和位置随工况的不同而变化。图1(a)给出了数值模型测点布置方案。由于初始压缩波在隧道内的传播规律具有一维特性[17]，故本文在距离隧道入口50，100，300，500 和950 m 的拱顶处分别设置5 个测点1 号～5 号，以监测隧道内瞬变压力的变化；高速铁路设计规范对隧道出口20 m 和50 m 处微气压波峰值做了相关规定[11]，故在距离隧道出口20 m 和50 m，距轨顶面1.5 m 处，分别设置2 个测点6 号和7 号，以监测微气压波的变化。

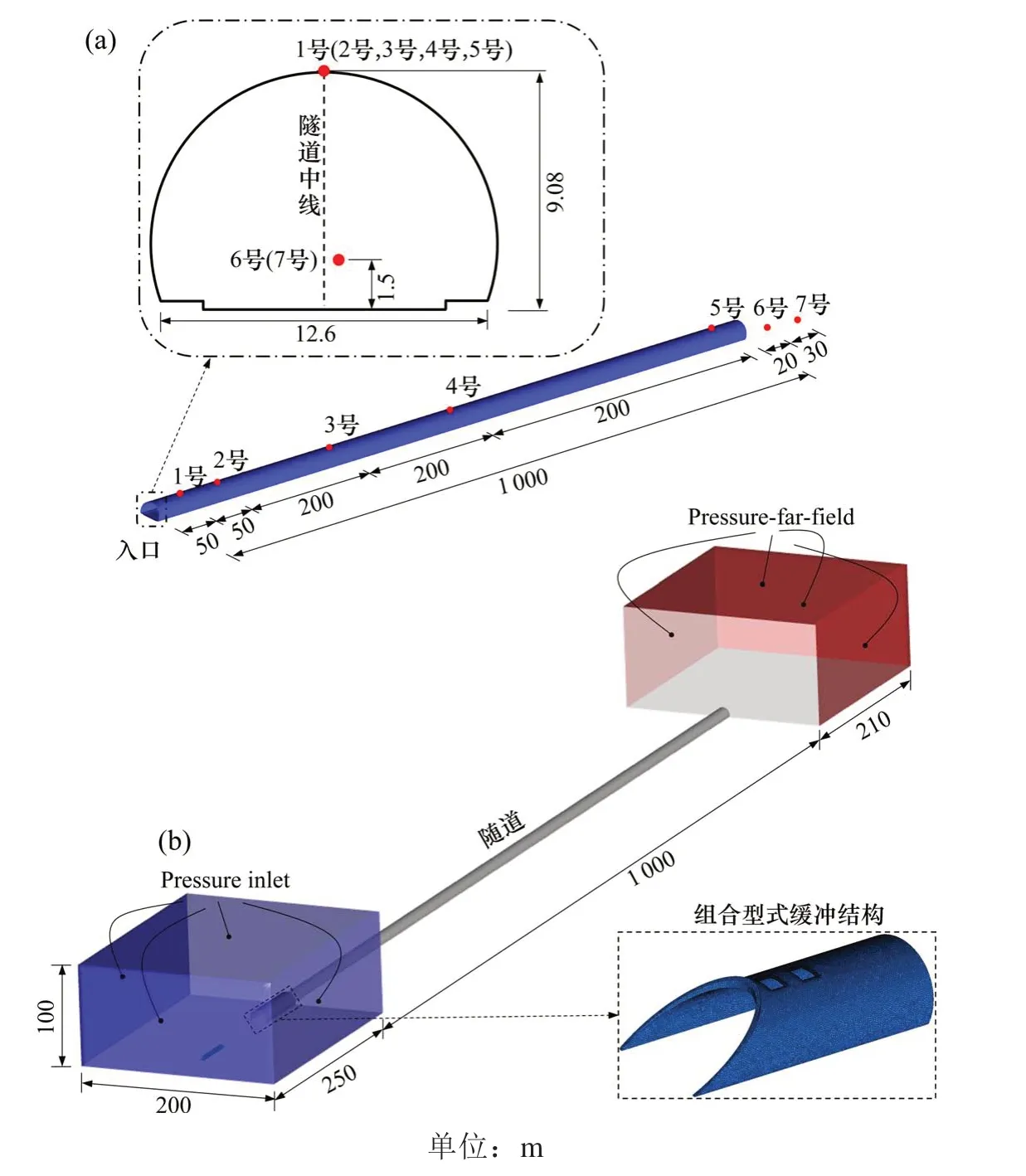
图1 几何模型Fig.1 Geometric model

如图1(b)所示，数值模拟采用1︰1 全尺模型，隧道两端的大气采用长方体进行模拟。入口端长方体的长宽高分别为250，200和100 m，出口端长方体的长宽高分别为210，200和100 m。模型主要边界条件有3 种类型：Pressure-inlet 边界条件被用于隧道入口端的大气域的两侧、顶部及后端；Pressure-far-field 边界条件被用于隧道出口端大气域的两端、顶部及后端；隧道壁面、缓冲结构壁面、地面及隧道两端大气域靠近山体的壁面则采用No-slip wall，缓冲结构壁面粗糙度Ks=0.005 m，粗糙长度Cs=0.08。初始条件下设置车头鼻尖离隧道入口的距离为130 m，使列车在大气中运行1 s左右，保证列车周围流场稳定。

1.2 网格策略及求解设置

采用滑移网格技术结合RNGk-ε双方程湍流模型[18-19]，通过结构网格和非结构网格结合的技术对计算域进行划分，如图2所示。整体网格区域被划分为静网格(A)和动网格(B)这2 个部分，各区域之间通过Interface 实现流场信息交换，如图2(b)所示。其中，静网格(A)又进一步被划分成大气区域(A1)和缓冲结构区域(A2)这2 个部分，大气区域(A1)为隧道两端和隧道内空气部分，采用六面体结构化网格，缓冲结构区域(A2)为包含缓冲结构的一个长方体区域，采用四面体非结构化网格。动网格(B)为包含列车附近区域(B1)和前、后端(B2，B3)铺层区域，均采用六面体结构化网格。车体表面网格尺寸为0.1 m，在列车表面设置8 层附面层，附面层的初始厚度为1 mm，对应的y+≈30[20]，附面层网格按1.1 的比率向外扩展。前、后铺层区域(B2，B3)的纵向网格尺寸为1 m。

图2 模型网格示意图Fig.2 Model grid diagram

为验证本文模型网格独立性，通过调整模型核心加密区，建立粗(800 万)、中(1 500 万)和细(2 500 万)3 种不同网格数量的模型，均采用相同的模型工况和计算设置。图3 为测点2 号的初始压缩波时程曲线对比，由图可知1 500 万个网格单元模型的计算结果和2 500 万个网格单元模型的计算结果比较吻合，而800万个网格单元模型的计算结果差异较大。为平衡计算精度和计算效率，采用1 500万网格模型，最小网格质量为0.2，集中于帽檐斜切段的狭缝处，但数量小于整体网格数的0.002%。FLUENT 软件以网格正交质量为检查标准，通常在前处理中保持正交质量在0.15 以上，方可满足求解器的要求，故本网格模型满足FLUENT 的计算要求。基于FLUENT 软件，对隧道内流场采用Pressure-based 求解器进行求解，控制方程的离散方式为有限体积法(FNM)，采用半隐式算法(SIMPPLE)对压力与速度耦合方程进行求解[21]，采用2 阶迎风格式(Second Order Upwind)对时间积分和动量方程进行求解。物理时间步长均设置为10-3s[22]，残差的最小收敛值为10-4[23]，每个时间步的迭代次数为30次。

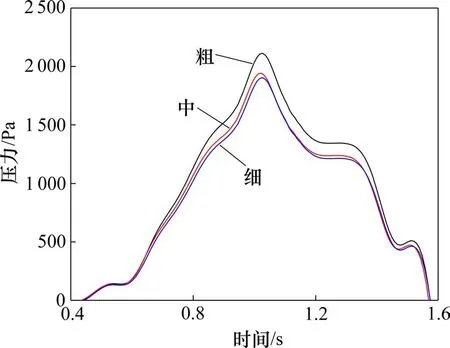
图3 不同网格数量条件下初始压缩波对比Fig.3 Pressure curves of initial compression wave under different grid numbers

1.3 工况方案及研究思路

图4 给出了本研究的工况拟定方案及研究思路。相关研究及工程实践表明[24]，一般首个开孔到缓冲结构边缘的距离为30 m 以下，本研究分别选取了4，8，16 和24 m 进行研究，确定首个开孔到帽檐的最优距离。基于首个开孔到帽檐的最优距离，对开孔率α展开研究(α=Sk/St，式中Sk和St分别为开孔面积和隧道断面面积)[10,24]，对比开孔率α(24%，32%，40%和48%)的泄压效果，确定最优开孔率。再基于首个开孔到帽檐的最优距离和最优开孔率，对比不同开孔数量(2 个、4 个和8 个)的泄压效果，确定最优开孔数量。然后基于上述最优工况，分析不同环向位置(拱顶、拱腰单侧和拱腰双侧)的泄压效果，最后提出等截面扩大+帽檐斜切+泄压孔的组合型式缓冲结构的最佳优化参数。

图4 工况方案及研究思路Fig.4 Condition scheme and research ideas

2 模型验证

通过现场实测数据与数值模拟进行对比，分别对隧道内瞬变压力和隧道洞口微气压波进行验证。本次现场实测试验以某高速铁路隧道为测试对象，其设计时速为350 km，隧道全长5 934 m，净空面积为100 m2。采用微压差传感器输出压力信号，再分别使用A/D 板和2801 采集系统采集压力波和微气压波数据，最后通过USB 数据线实现数据与计算机联通。图5为本次现场实测的测点布置示意图，其中S1 为隧道内瞬变压力测点，S2 为隧道洞口微气压波测点。

图5 现场实测测点布置示意图Fig.5 Field measurement point layout diagram

图6 分别给出了现场实测和数值模拟2 种情况下，隧道内S1 测点首波瞬变压力的时程曲线对比和隧道洞口S2 测点微气压波的时程曲线对比。由图6分析可得数值模拟和现场实测的隧道内瞬变压力变化规律，其波形基本一致。数值模拟计算得到的隧道内瞬变压力峰值略小于现场实测得到的结果，正压峰值相对误差为1.86%，负峰值相对误差为-5.41%；数值模拟得到的隧道洞口微气压波时程曲线负波峰的波动幅度明显超出现场实测得到的时程曲线，两者之间的正压峰值相对误差为7.63%。产生差异的原因可能是：数值模拟和现场实测不可避免地存在隧道壁面及列车车头粗糙度的差异。然而，本研究着重于对微气压波的形成机理和峰值变化规律进行分析，可认为本文数值模拟方法和计算结果是合理的。

图6 现场实测和数值模型时程曲线对比Fig.6 Comparison of field measurement and numerical model

3 结果分析与讨论

3.1 首个泄压孔边缘到帽檐的距离

图7 为采用4 种不同的首个泄压孔边缘到帽檐距离的组合型式缓冲结构，距离分别为4，8，16和24 m，均在拱顶中部设置2 个大小一致的泄压孔。泄压孔的宽度Dk=4 m，长度Lk=4 m。

装配路径反映了零组件在安装过程中的运动路径，在虚拟装配过程中依据装配技术要求，考虑装配工艺性、可装配性分层逐级生成零组件的装配顺序和装配路径，依据设计好的工艺流程、装配顺序和装配路径对零组件、资源在装配过程中与其他零组件、资源的干涉等进行仿真。当存在干涉情况时，给出干涉报警同时给出干涉量和干涉区域[3]。装配路径规划和干涉分析如图5和图6所示。

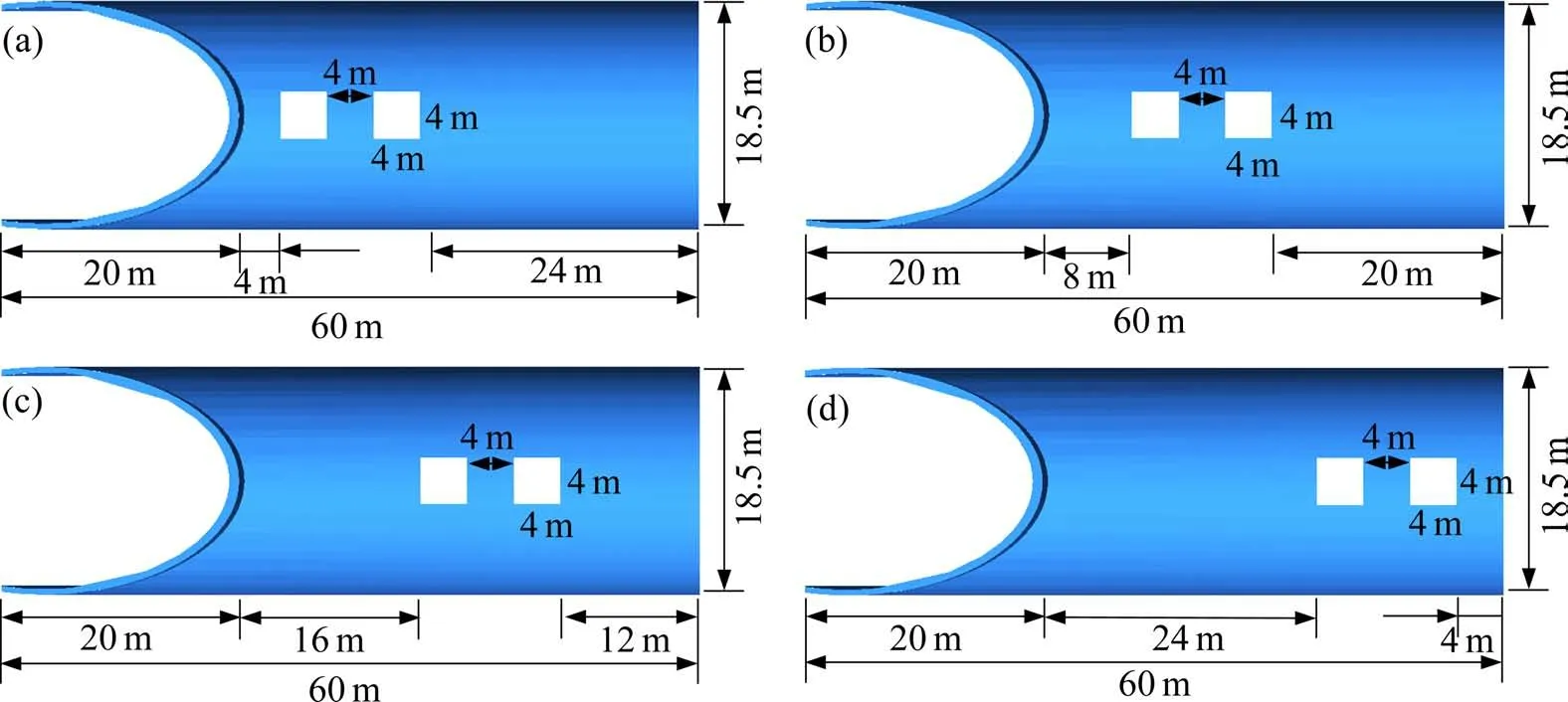
图7 首个泄压孔边缘到帽檐不同距离的组合型式缓冲结构示意图Fig.7 Combined buffer structure with dfferent distances between the first ventilation window and the hat

图8 为采用不同纵向开孔位置的缓冲结构时，隧道内2 号测点的初始压缩波和压力梯度时程曲线。表1为隧道内各测点的初始压缩波和压力梯度峰值对比表。由图8 和表1 分析可得：初始压缩波压力时程曲线的开始上升速率随泄压孔边缘到帽檐距离的增加而不断降低，但峰值不断升高。相比于泄压孔边缘到帽檐的距离为4 m，当距离为8，16 和24 m 时，1 号测点的初始压缩波峰值分别增加2.9%，5.6%和5.2%，5 号测点的初始压缩波峰值分别增加5.6%，14.8%和19.8%。

表1 首个泄压孔边缘到帽檐不同距离下初始压缩波和压力梯度峰值Table 1 Peak value of initial compression wave and pressure gradient under different distances

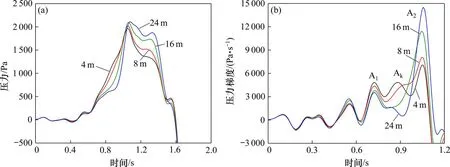
图8 不同首个泄压孔边缘到帽檐的距离下初始压缩波和压力梯度时程曲线Fig.8 Pressure curves of initial compression wave and pressure gradient under different distances

由图8 和表1 还可得：压力梯度时程曲线出现很明显的3 个波峰A1，A2和Ak，各波峰峰值出现时间基本一致。当泄压孔边缘到帽檐的距离增加，列车经过缓冲结构泄压孔产生的波峰A1不断减小，Ak逐渐消失，而A2不断增大，压力梯度峰值也不断增加。产生上述现象的原因可能是：随着泄压孔边缘到帽檐距离的增大，Ak出现时间不断滞后。当泄压孔与隧道入口接近时，波峰Ak与列车进入隧道产生的波峰A2重合，压力梯度峰值反而上升，从而使初始压缩波上升速率加快，峰值增大。

图9 为不同纵向开孔位置下隧道出口20 m 和50 m处微气压波时程曲线。由图9分析可得，采用不同泄压孔边缘到帽檐的距离下，隧道出口微气压波时程曲线出现2 个不同的波峰A1和A2，但泄压孔边缘到帽檐的距离增加，波峰A1的峰值不断降低，波峰A2的峰值不断升高。在距离隧道出口20 m处，当泄压孔边缘到帽檐的距离为4 m时，微气压波峰值最小，相比于距离为8，16 和24 m 的情况，其微气压波峰值分别降低了14.4%，39.5%和50.7%。在距离隧道出口50 m 处，将泄压孔边缘到帽檐的距离为4，8，16 和24 m 时，其微气压波峰值分别为19，22，31 和39 Pa，仅泄压孔边缘到帽檐的距离为4 m 的情况下满足规范要求(20 Pa)。

图9 首个泄压孔边缘到帽檐不同距离下微气压波时程曲线Fig.9 Pressure curves of micro-pressure wave under different distances

综上所述，组合型式缓冲结构的首个泄压孔到帽檐的距离为4 m 时，能较好地缓解隧道洞口微气压波。

3.2 开孔率

图10 给出了开孔率α为24%，32%，40%和48%这4 种组合型式缓冲结构的主要尺寸，均在拱顶中部设置2个大小一致的泄压孔。泄压孔的宽度Dk=4 m，长度Lk=3，4，5 和6 m，2 个泄压孔之间的净距均为4 m，泄压孔边缘距离帽檐的距离均为4 m。

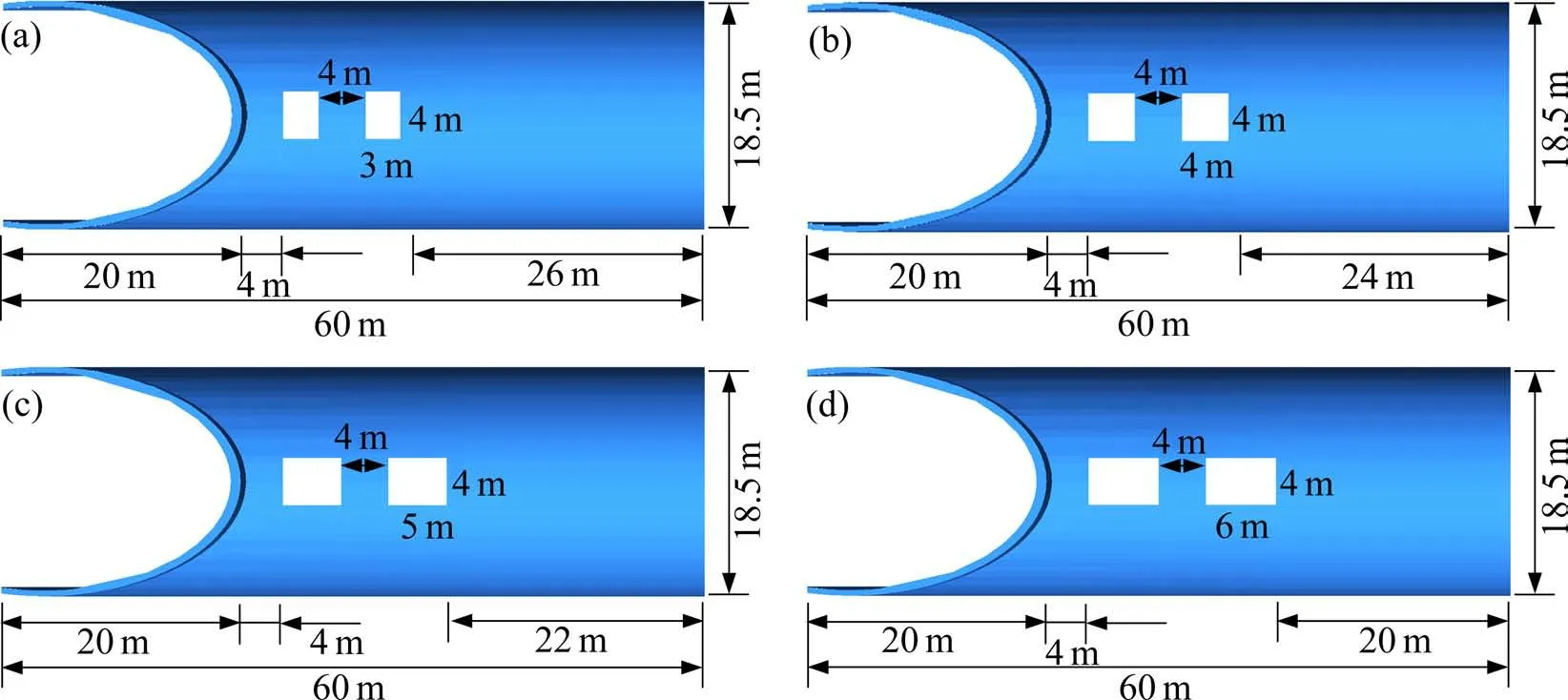
图10 不同开孔率组合型式缓冲结构示意图Fig.10 Combined buffer structure with different ventilation ratios

图11 为当列车通过不同开孔率的组合型式缓冲结构时，隧道内2号测点的初始压缩波和压力梯度时程曲线。表2为隧道内不同测点的初始压缩波和压力梯度峰值。由图11 和表2 分析可得：不同开孔率下初始压缩波时程曲线的变化规律基本一致，压力开始上升和峰值出现时间基本一致，但开孔率越大，初始压缩波开始上升速率越慢，随后上升速率逐渐升高，各测点初始压缩波峰值不断增大。当开孔率α=48%时，初始压缩波峰值略高于其他低开孔率条件下的峰值，相比于α=24%，1 号～4 号测点初始压缩波峰值差异最高仅有4%，5 号测点初始压缩波峰值也仅相差10%，说明开孔率对初始压缩波峰值影响较小。

表2 不同开孔率下初始压缩波和压力梯度峰值Table 2 Peak value of initial compression wave and pressure gradient under different ventilation ratios

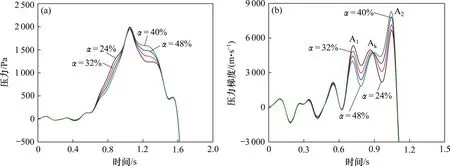
图11 不同开孔率下初始压缩波和压力梯度时程曲线Fig.11 Pressure curves of initial compression wave and pressure gradient under different ventilation ratios

由图11 和表2 还可得：不同开孔率下同一波峰峰值及相同开孔率下不同波峰的峰值之间均存在一定的差异。例如：对于α=24%，Ak的峰值最小，A2最大；对于α=32%，40%和48%，A1的峰值最小，A2最大。对于不同测点，压力梯度峰值随组合型式缓冲结构开孔率的变化存在显著差异，例如：对于1号和2号测点，峰值随开孔率的增加不断增大；对于3号～5号测点，当α=24%时，初始压缩波峰值最低，当α=32%时，压力梯度峰值最低。

综上所述，在组合型式缓冲结构的开孔率为32%时，缓冲结构能较好地缓解隧道洞口微气压波。

3.3 泄压孔数量

在首个泄压孔边缘到帽檐距离为4 m，开孔率α=32%条件下，当泄压孔数量不同时，分析初始压缩波和微气压波的变化规律。图13 给出了在拱顶分别设置2 个、4 个和8 个泄压孔的组合型式缓冲结构的尺寸。

图13 不同泄压孔数量组合型式缓冲结构示意图Fig.13 Combined buffer structure with different number of ventilation windows

图14 为当列车通过不同泄压孔数量的组合型式缓冲结构时，隧道内2号测点的初始压缩波和压力梯度时程曲线。表3为隧道内不同测点的初始压缩波和压力梯度峰值。由图14 和表3 分析可得：在不同泄压孔数量条件下，隧道内初始压缩波时程曲线变化规律基本一致，仅上升和下降过程中的快慢程度略有偏差。泄压孔数量对初始压缩波峰值几乎无影响，各测点初始压缩波峰值的差异保持在30 Pa 以内，但总体而言，当泄压孔数量为8 个时，初始压缩波峰值略低于其他条件下的峰值。泄压孔数量对压力梯度的影响较显著，不同泄压孔数量下压力梯度时程曲线均出现3 个波峰，第3 个波峰的峰值最大。1 号～4 号测点压力梯度峰值随开孔数量的增加先升高后降低，当泄压孔数量为8 时，峰值最小。5 号测点压力梯度峰值随开孔数量的增加先降低后升高，当泄压孔数量为4时，峰值最小。

表3 不同泄压孔数量下初始压缩波和压力梯度峰值Table 3 Peak value of initial compression wave and pressure gradient under different number of ventilation windows

图15(a)为隧道洞口20 m 处不同泄压孔数量下微气压波时程曲线，图15(b)为隧道出口20 m 和50 m 处微气压波峰值随泄压孔数量的变化规律。由图15 分析可得：当列车通过不同泄压孔数量的组合型式缓冲结构时，隧道出口20 m 处微气压波时程曲线变化规律基本一致，均出现2个波峰。当泄压孔数量为4 个时，2 个波峰峰值差异最小，峰值分别为45.2 Pa 和45.1 Pa，仅相差0.22%；当泄压孔数量为8 个时，2 个波峰峰值差异最大，分别为48.7 Pa和41.3 Pa，相差达到17.9%。

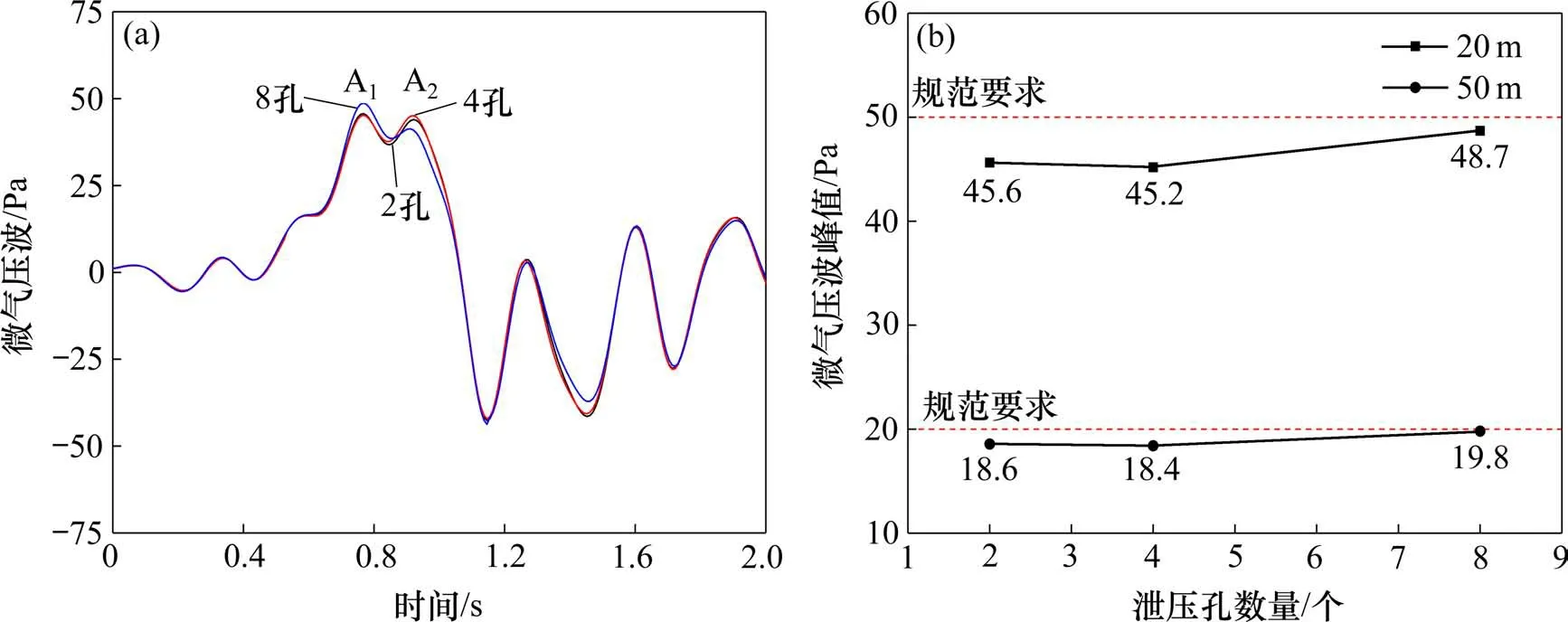
图15 不同泄压孔数量下微气压波的时程曲线和峰值Fig.15 Pressure curves and peak value of micro-pressure wave under different number of ventilation windows

综上所述，组合型式缓冲结构的开孔数量为4个时，缓冲结构能较好地缓解隧道洞口微气压波。

3.4 泄压孔环向位置

在首个泄压孔边缘到帽檐距离为4 m，开孔率α=32%，泄压孔数量为4 个条件下，当泄压孔环向位置不同时，分析初始压缩波和微气压波的规律。图16 为泄压孔分别布置在拱顶、拱腰单侧和拱腰双侧3种不同环向位置的组合型式缓冲结构。每个泄压孔的尺寸均为2 m(纵向)×4 m(横向)，拱腰泄压孔顶部距离轨顶面3 m。

图16 不同环向开孔的组合型式缓冲结构示意图Fig.16 Combined buffer structure with different circumferential ventilation windows

图17 为列车驶入不同环向开孔位置的组合型式缓冲结构时，隧道内2号测点的初始压缩波和压力梯度时程曲线。表4为隧道内不同测点处的初始压缩波和压力梯度峰值。由图17 和表4 分析可得：泄压孔在缓冲结构环向上的分布位置对隧道内初始压缩波时程曲线和峰值的影响十分微弱，但对压力梯度时程曲线和峰值的影响十分显著。对于压力梯度时程曲线，不同环向开孔位置下，其时程曲线均出现3 个较明显的波峰(A1，Ak和A2)，但峰值之间的变化规律略有不同。当在拱腰单侧布置4个泄压孔时，波峰A1的峰值(4581 Pa)最小，波峰A2的峰值(6 460 Pa)略大于Ak的峰值(6 589 Pa)；当在拱腰两侧各布置2个泄压孔时，波峰Ak的峰值(7 020 Pa)显著大于A2的峰值(6 185 Pa)。对于压力梯度峰值，针对受列车运行影响较小的隧道洞身段(4 号测点)和出口段(5 号测点)，当在组合型式缓冲结构的拱腰两侧各开2个泄压孔时，压力梯度峰值最大；当在拱顶设置4个泄压孔时，压力梯度峰值最小。

表4 不同环向开孔位置下初始压缩波和压力梯度峰值Table 4 Peak value of initial compression wave and pressure gradient under different circumferential ventilation windows

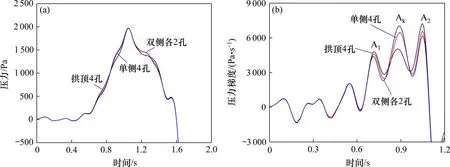
图17 不同环向开孔位置下初始压缩波和压力梯度时程曲线Fig.17 Pressure curves of initial compression wave and pressure gradient under different circumferential ventilation windows

图18为隧道洞口20 m 和50 m 处不同环向开口位置下微气压波时程曲线。由图18 分析可得：隧道内初始压缩波的压力梯度变化规律最终体现在微气压波时程曲线和峰值上。不同开孔位置下的微气压波时程曲线均出现2个较明显波峰，A1波峰之间的峰值差异较小，而A2波峰之间的峰值差异较大。当在组合型式缓冲结构的拱腰两侧各开2个泄压孔时，隧道出口微气压波峰值最大，20 m 和50 m 处的峰值分别为56 Pa 和22 Pa，不满足规范要求；当在拱顶设置4个泄压孔时，微气压波峰值最小，20 m 和50 m 处的峰值分别为45 Pa和18 Pa，相对于拱腰两侧各开2 个泄压孔，降低了20%和18%。

图18 不同环向开孔位置下微气压波时程曲线Fig.18 Pressure curves of micro-pressure wave under different circumferential ventilation windows

综上所述，在组合型式缓冲结构等截面扩大段拱顶设置泄压孔时，缓冲结构能较好地缓解隧道洞口微气压波。

4 结论

1) 现场实测和数值模拟2种方法相互验证，两者所得的微气压波变化规律基本一致，正压峰值误差为7.63%。

2) 当组合型式缓冲结构的首个泄压孔边缘到帽檐的距离为4 m 时，对微气压波的缓解效果最佳，相比于距离为8，16 和24 m，其隧道出口20 m 处的微气压波峰值分别降低14.4%，39.5%和50.7%。

3) 当采用开孔率α为32%的组合型式缓冲结构时，对微气压波的缓解效果最佳，相较于开孔率为24%，40%和48%，其隧道出口20 m 处的微气压波峰值分别降低5.7%，9.1%和19.7%。

4) 在组合型式缓冲结构拱顶设置4 个4 m(横向)×2 m(纵向)的泄压孔时，对微气压波的缓解效果最佳，相较于设置2 个和8 个泄压孔，其隧道出口20 m处的微气压波峰值分别降低0.9%和7.2%。

5) 组合型式缓冲结构的环向位置上，在拱顶设置泄压孔时，对微气压波的缓解效果最佳，相较于在拱腰单侧或双侧对称设置泄压孔，其隧道出口20 m 处的微气压波峰值分别降低14.2%和19.3%。