直墙拱形巷(隧)道岩爆卸压孔解危效应试验研究
王宇晨 张晓君 刘 啸
(1.山东理工大学资源与环境工程学院,山东 淄博 255000;2.山东理工大学矿山工程技术研究所,山东 淄博 255000)
近些年,岩爆控制研究取得了不小进展。在岩爆解危方法与技术中,施工卸压孔是常用的,在卸压孔解危效应机理研究方面,刘宏军[1]针对卸压孔开展了理论分析,文献[2-5]采用数值模拟技术针对钻孔卸压作用机理开展了研究,宋希贤等[6]开展了动力扰动下深部巷道卸压孔与锚杆联合支护的作用机理研究,张士川等[7]针对卸压孔破裂演化及布置参数开展了研究,齐燕军等[8]分析和讨论了不同卸压孔直径下煤柱破坏特征、强度特征及声发射特性,赵振华等[9]开展了含卸压孔硬岩应力松弛特性试验研究,张晓君等[10-11]提出卸压孔劈裂的局部解危方法并开展了3种劈裂角度的室内试验和基于RFPA软件的数值试验。目前尚缺乏具体针对直墙拱形巷(隧)道岩爆开展卸压孔解危效应方面的研究。
综上,本研究将具体针对直墙拱形巷(隧)道,基于声发射和应变等监测,结合岩爆内因分析,开展含卸压孔的直墙拱形巷(隧)道花岗岩试样双轴压缩试验,得到其卸压孔解危效应机理,为岩爆破裂演化及解危提供依据。
1 直墙拱形巷(隧)道岩爆卸压孔解危效应试验
1.1 试验装置与方案
采取湖南某地花岗岩,该岩石为中细粒结构,主要矿物成分为斜长石和石英,同时含有少量云母,此外还存在微量的角闪石,质地硬脆,满足岩爆内因要求,具体的矿物成分及其含量见表1。

表1 矿物成分及其含量Table 1 Mineral composition and its content %
首先加工制成标准圆柱形试样和巴西劈裂圆盘试样,得到花岗岩单轴抗压强度平均值为154 MPa,单轴抗拉强度平均值为7.2 MPa,根据压拉比及基于压拉比的强度脆性系数法,判定其具有中等岩爆倾向性,满足岩爆内因要求。
加工成尺寸为100 mm×100 mm×50 mm的长方体试样,对试样进行多位置超声波测试,测得波速在2 778~2 941 m/s之间(图1),平均波速为2 868 m/s,变异系数ρ为0.028,可见试样不同位置之间的波速差别很小。
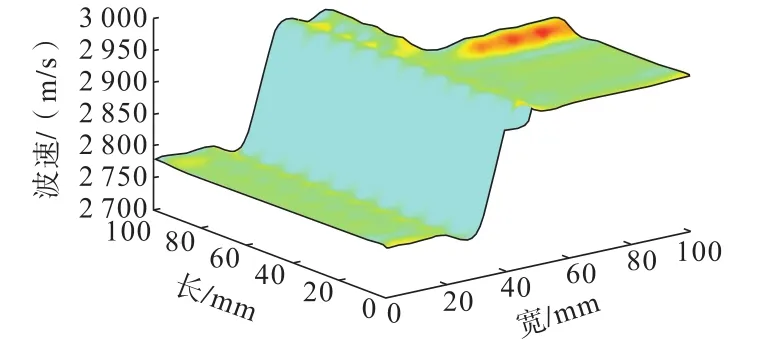
图1 试样纵波波速Fig.1 Longitudinal wave velocity of the sample
当X为服从[0,1]均匀分布的随机变量时,则V服从Weibull分布:
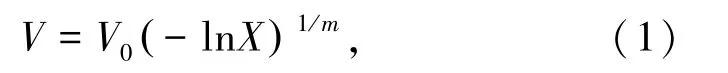
式中,V为波速随机变量;V0为波速的平均值;X为服从[0,1]均匀分布的随机变量;m为均质度[12-14]。m值越大,波速变量越趋于一致,变异系数ρ也就越小,岩石就越均质,可见,本研究所用试样均质性较好,满足岩爆内因要求。
在长方体试样中心施工直墙半圆拱形巷(隧)道,巷(隧)道宽为20 mm,直墙和拱高部分均为10 mm,具体试样见图2(a)。根据试样尺寸和制样条件,在巷(隧)道两帮分别施工4个卸压孔,孔直径5 mm,孔中心间距10mm,孔中心距离试样底面均为47 mm,外侧孔中心距离试样正、背面分别为10 mm,见图2(b)、图2(c)。这里需要说明的是,试样相关尺寸不对应具体的巷(隧)道,也不适用相似比。

图2 试样Fig.2 The samples
直墙拱形巷(隧)道岩爆试验是在自制的真三轴加卸载试验系统上进行,见图3。根据现场巷(隧)道的岩爆应力演化情况,分别针对巷(隧)道试样和含卸压孔的巷(隧)道试样开展双轴压缩试验,垂直方向位移加载速率为0.1 mm/s,具体加载方案:X水平向保持施加10 MPa载荷,Z垂直向以10MPa逐级施加载荷直到试样整体破坏。布置应变监测系统,采用DH3818静态应变电阻测试仪,在试样正面的巷(隧)道两侧帮布置应变监测,监测其垂直和水平应变的变化,应变片型号为BFH120-15AA,见图3(a)。这里需要说明的是,水平向应变监测位置是在试样表面且在巷(隧)道围岩两侧帮靠近底板的位置,实测值尤其是拉应变值将低于两侧帮其他位置,若该位置产生拉应变则其他位置必定产生拉应变。布置声发射监测系统,采用北京软岛时代科技有限公司生产的DS5系列声发射仪器,在试样的背面布置声发射探头,布置位置见图3(b)。在试验系统观察口布置摄像机摄录试样正面全程的变形破坏情况,具体见图3(c)。

图3 试验系统Fig.3 The test system
1.2 试验结果与卸压孔解危效应分析
无卸压孔直墙拱形巷(隧)道试样的垂直应力与应变的关系曲线见图4。可见试样从加载初期到后期基本呈现弹性变形阶段,无明显压密阶段和塑性变形阶段,载荷达到150 MPa时试样整体爆裂,曲线陡降,残余应力为30.8 MPa,应力降低率0.795,试样总垂直变形仅为1.8 mm,硬脆性明显。
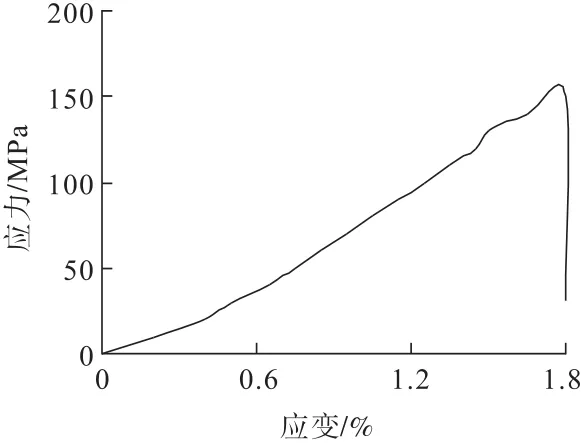
图4 无卸压孔试样垂直应力与应变的关系Fig.4 The relationship between the vertical stress and strain with no pressure relief holes
无卸压孔试验监测应变与垂直应力的关系见图5,加载载荷达到70 MPa时,左侧水平向监测应变值转为正,呈现拉应力,加载载荷达到90 MPa时,右侧水平向监测应变值转为正,呈现拉应力,随加载载荷的增加,拉应力不断增大,当拉应力超过其抗拉强度时,围岩将产生拉破坏,表现为片剥或颗粒弹射等。从加载载荷130 MPa开始,关系曲线开始发生突变,水平向应变突增,垂直向应变突降,说明直墙拱形巷(隧)道两侧帮已出现破坏。
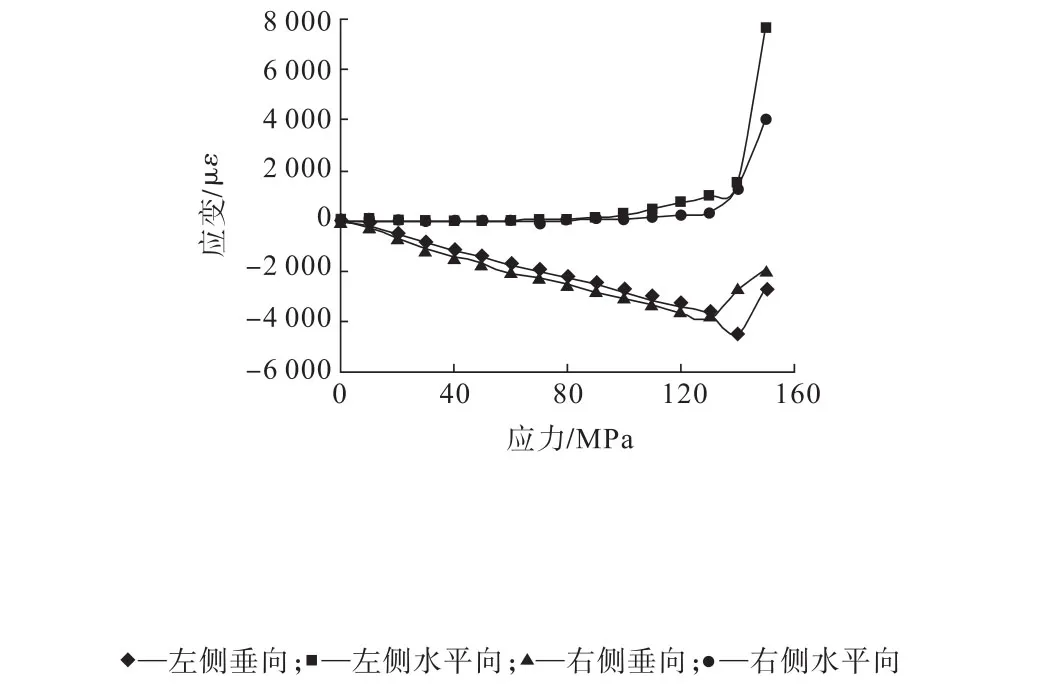
图5 无卸压孔试样监测位置的应变与垂直应力的关系Fig.5 The relationship between the strain and the vertical stress at the monitoring position with no pressure relief holes
加载载荷达到100 MPa时无卸压孔直墙拱形巷(隧)道围岩产生颗粒弹射,见图6(a)。加载载荷达到110MPa时巷(隧)道两侧帮围岩产生片剥并伴随噼啪声响,见图6(b)。加载载荷达到120 MPa时巷(隧)道两侧帮围岩片剥和弹射范围进一步扩大,见图6(c)。加载载荷达到130 MPa时巷(隧)道两侧帮围岩片剥向深部不断发展,见图6(d)。加载载荷达到150MPa时试样整体爆裂,巷(隧)道两侧帮是试样整体爆裂的源头,巷(隧)道两侧帮严重破坏,形成V形爆坑,见图6(e),从侧面破坏形式可见,试样呈现明显的劈剪复合破坏。综上,巷(隧)道围岩的破裂演化与前述应变监测结果是一致的。

图6 无卸压孔破坏形式Fig.6 The failure modes of the sample with no pressure relief holes
有卸压孔的直墙拱形巷(隧)道试样的垂直应力与应变的关系曲线见图7。可见试样同样从加载初期到后期基本呈现弹性变形阶段,无明显压密阶段和塑性变形阶段。载荷达到90 MPa时试样整体爆裂,曲线陡降,残余应力为23.6 MPa,应力降低率0.738,试样总垂直变形为1.15 mm。相比未施工卸压孔的情况,施工卸压孔后其承受的最大载荷明显下降,最大载荷下降了40%,破坏时的应力降低率也明显下降。同等情况下的变形有所增加,说明施工卸压孔后,降低了侧帮围岩完整性,降低了承载能力,降低了应力降低率,起到了明显的岩爆解危效果。
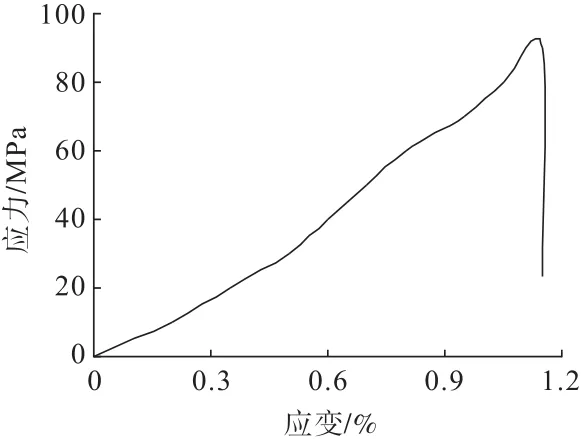
图7 有卸压孔试样应力与应变的关系Fig.7 The relationship between stress and strain with pressure relief holes
有卸压孔试验监测应变与垂直应力的关系如图8所示。从加载开始,左侧水平向监测应变值一直为正,呈现拉应力并不断增大,加载载荷达到70 MPa时,右侧水平向监测应变值转为正,呈现拉应力,但关系曲线未发生突变,当拉应力超过其抗拉强度时,围岩将产生拉破坏,表现为片剥或颗粒弹射等。
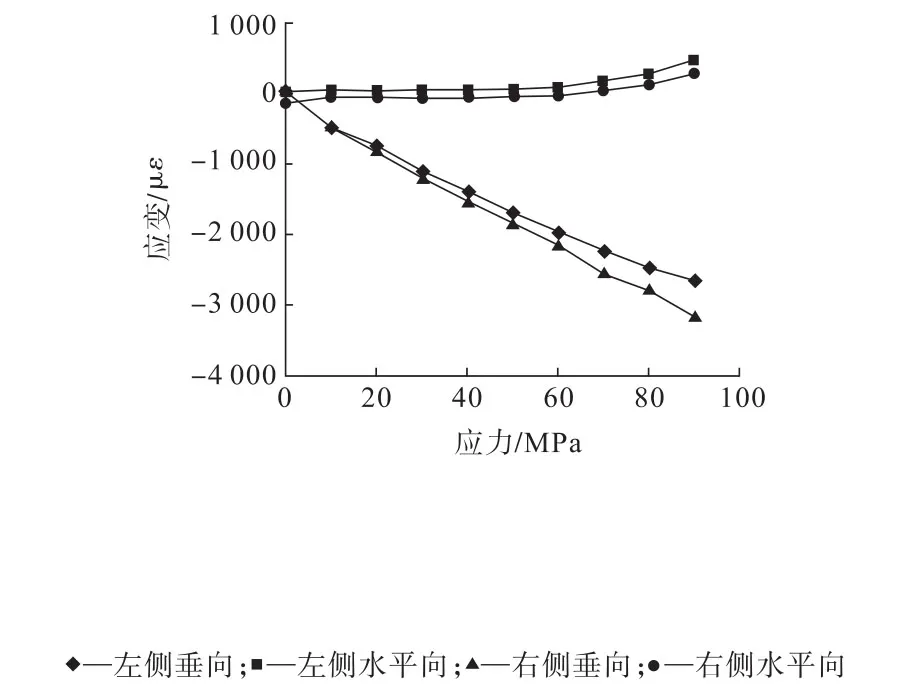
图8 有卸压孔试样垂直载荷与监测应变的关系Fig.8 The relationship between vertical load and monitoring strain with pressure relief holes
加载载荷达到60 MPa时有卸压孔直墙拱形巷(隧)道左侧帮卸压孔位置产生片剥,具体见图9(a)。加载载荷达到70 MPa时巷(隧)道两侧帮卸压孔位置均产生片剥,具体见图9(b)。加载载荷达到90 MPa时试样整体爆裂,具体见图9(c)。巷(隧)道围岩的破裂演化与前述应变监测结果是一致的。巷(隧)道两侧帮卸压孔位置是试样整体爆裂的源头,试样虽然整体破坏,但巷(隧)道两侧帮破坏不严重,破坏也主要集中在卸压孔位置,具体见图9(d)。试样侧面的破坏形式见图9(e),可见破裂演化均从卸压孔两侧开始,产生明显的翼裂纹并扩展至边界,卸压孔由圆形变成椭圆形,卸压孔对试样破裂演化起到了关键性控制作用。综上,与未施工卸压孔的情况相比,巷(隧)道围岩破坏范围大为缩小,破坏程度大为降低,卸压孔控制着整个围岩破裂演化的进程,起到了明显岩爆解危效果。

图9 有卸压孔破坏形式Fig.9 The failure modes of the sample with pressure relief holes
不含卸压孔的直墙拱形巷(隧)道声发射监测结果见图10(a),其阶段最大能量释放量为5 071 868.44 mV·ms。含卸压孔的直墙拱形巷(隧)道声发射监测结果见图10(b),其阶段最大能量释放量为1 696 236.08 mV·ms。可见施工卸压孔致使其峰值能量释放量大为下降。根据前面的分析知,含卸压孔试样虽然整体破坏,但巷(隧)道两侧帮破坏不严重,破坏也主要集中在卸压孔位置,其能量释放也主要集中在卸压孔及由卸压孔引发的裂纹产生、扩展和贯通等,对于巷(隧)道本身而言,岩爆并不明显,岩爆剧烈程度大为降低,卸压孔起到了明显岩爆解危效果。
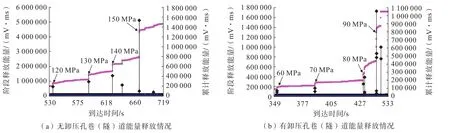
图10 巷(隧)道能量释放与到达时间的关系Fig.10 The relationship between energy release and arrival time of roadway (tunnel)
2 岩爆卸压孔解危效应的损伤演化探讨
根据能量释放监测结果,可采用能量释放量来表示损伤变量D。

式中,S1为阶段累计能量释放量;S为总能量释放量。根据试验得到的巷(隧)道能量释放量随加载载荷的变化关系,可进一步得到无卸压孔巷(隧)道损伤变量Dw和有卸压孔巷(隧)道损伤变量Dx随加载载荷的变化关系,见图11。可见二者在接近载荷峰值时的损伤变量变化规律比较接近,这里需要说明的是,峰值时二者均是试样整体破坏,所以二者在接近峰值时的演化规律基本一致。接近峰值时的演化规律并不能代表巷(隧)道围岩本身损伤演化规律,二者在载荷前、中期的损伤变量演化规律有所不同,卸压孔的存在致使能量释放前移。
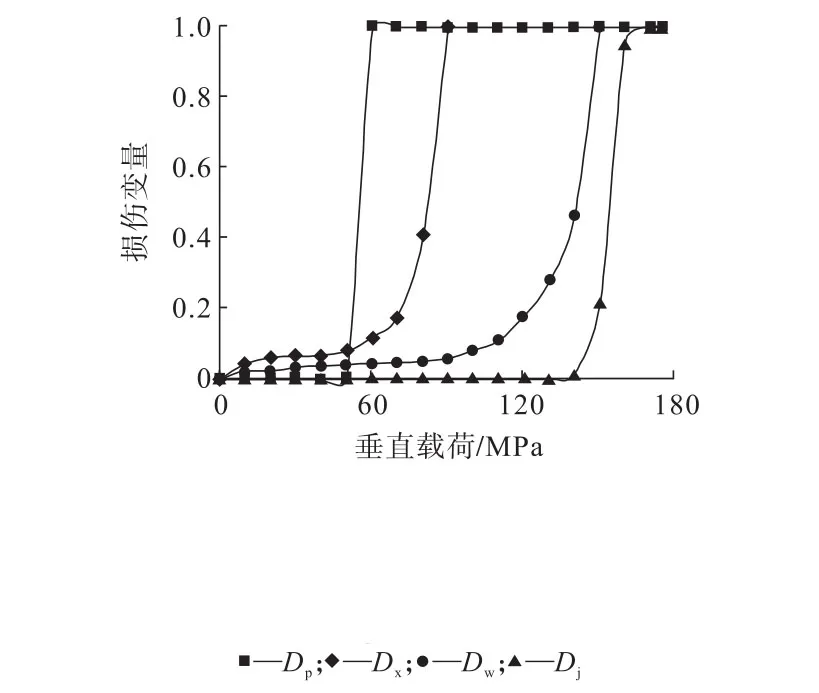
图11 试样垂直载荷与损伤变量的关系Fig.11 The relationship between vertical load and damage variable
随载荷的增加,直墙拱形巷(隧)道两侧帮在破裂演化早期主要是劈裂破坏,表现为片剥,若将岩石微元破坏概率作为损伤变量,得到巷(隧)道围岩临空面发生劈裂破坏的损伤变量Dp。
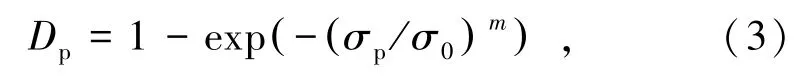
式中,σ0为岩石统计平均抗压强度;m为岩石均质度;σp为微元强度,其表达式为
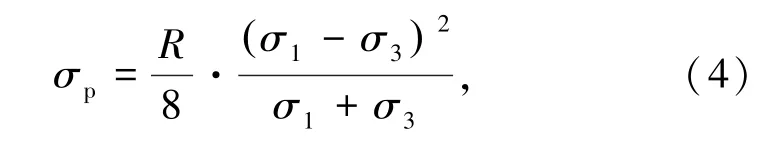
其中,R为岩石压拉比。根据试验情况,这里取m=39,R=21.4,σ0=154 MPa,σ3=0 MPa,得到损伤变量DP随加载载荷的变化关系见图11。从图11可见,损伤变量DP和Dw、Dx的变化规律是基本一致的,损伤变量DP接近1时的垂直载荷与本研究直墙拱形巷(隧)道片剥的临界载荷值接近。
随载荷的增加,直墙拱形巷(隧)道两侧帮在破裂演化中后期将产生剪切,呈现劈—剪复合破坏,同样将岩石微元破坏概率作为损伤变量,可得到临空面内部发生剪切破坏的损伤变量Dj。
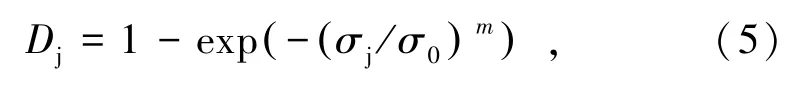
式中,σj为微元强度。
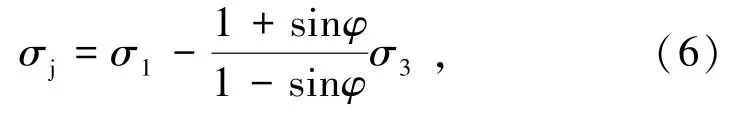
式中,φ为岩石内摩擦角。根据试验情况,这里取m=39,φ=60°,σ0=154 MPa,σ3=0.1 MPa,得到损伤变量Dj随加载载荷的变化关系见图11。从图11可见,损伤变量Dj和Dw、Dx的变化规律是基本一致的,损伤变量Dj接近1时的垂直载荷与本研究试样整体破坏时的峰值载荷非常接近。对比分析可见,损伤变量Dx演化进程与损伤变量DP演化进程更接近,损伤变量Dw演化进程与损伤变量Dj演化进程更接近,说明可以通过损伤变量DP、Dj的演化进程来预测岩爆的发生,施加卸压孔使巷(隧)道围岩破裂演化向完全劈裂方向演化发展。
3 结 论
(1)基于纵波波速,分析了花岗岩试样均质性;结合全过程应变和声发射监测等,进行了2种分别为无卸压孔和有卸压孔的直墙拱形巷(隧)道花岗岩试样双轴压缩试验,巷(隧)道两侧帮围岩片剥和弹射现象明显。
(2)与无卸压孔相比,施工卸压孔后其承受的最大载荷明显下降,最大载荷下降了40%,破坏时的应力降低率也明显下降,同等情况下的变形也有所增加,卸压孔的存在致使能量释放前移,起到了明显的岩爆解危效果。
(3)破裂演化均从卸压孔两侧开始,产生明显的翼裂纹并扩展至边界,卸压孔由圆形变成椭圆形,卸压孔对围岩破裂演化起到了关键性控制作用。与未施工卸压孔的情况相比,巷(隧)道两侧帮破坏不严重,破坏也主要集中在卸压孔位置,巷(隧)道围岩破坏范围大为缩小,破坏程度大为降低,卸压孔控制着整个围岩破裂演化的进程,起到了很好岩爆解危效果。
(4)分别建立了基于能量释放量的巷(隧)道围岩损伤变量表达式、基于岩石微元破坏概率的巷(隧)道围岩临空面发生劈裂破坏的损伤变量DP表达式和临空面内部发生剪切破坏的损伤变量Dj表达式。有卸压孔的巷(隧)道损伤变量Dx演化进程与损伤变量DP演化进程更接近。无卸压孔的巷(隧)道损伤变量Dw演化进程与损伤变量Dj演化进程更接近。可以通过损伤变量DP、Dj的演化进程来预测岩爆的发生,施加卸压孔使巷(隧)道围岩破裂演化向完全劈裂方向演化发展。

