基于局部离群因子的列车卫星定位故障检测方法
王韦舒,上官伟, ,刘江, ,姜维,
(1.北京交通大学 电子信息工程学院,北京 100044;2.北京市轨道交通电磁兼容与卫星导航工程技术研究中心,北京 100044)
随着卫星导航技术与铁路运输系统的深度融合,基于卫星导航的列车运行系统已经成为下一代列车运行控制系统的重要发展方向。全球卫星导航系统(Global navigation satellite system,GNSS)具有全天候、全天时、高精度的定位特性,能够为列车运行提供精准的位置服务,有助于降低对地面轨旁设备的依赖,降低运营维修成本[1]。然而,卫星信号传播过程中容易受到钟跳、钟漂、轨道参数建模误差等的影响而产生阶跃故障或斜坡故障[2]。这对于安全苛求的列车运行控制系统而言是难以容忍的,必须采取相应的处理手段保障卫星导航定位结果的可靠性。故障检测是保障用户端实现空间位置可靠解算的重要技术,其基本原理是利用统计假设检验的方法对冗余观测信息进行一致性检验,识别可能引起较大定位误差的故障卫星,进而保障定位结果的可靠性[3]。目前,故障检测方法根据历元量测信息的使用可分为快照式和序贯式。经典的快照式方法主要包括伪距比较法[4]、最小二乘残差法[5]和解分离法[6]。快照法仅仅采用当前时刻的观测值,对阶跃故障有较好的检测性能,但对于斜坡故障敏感性较低。而序贯法充分利用了多个历元数据之间的关联性,对缓慢增长的斜坡故障具有较好的检测效果。序贯法以滤波估计算法为基础,在状态估计中,滤波跟踪误差的存在使得新息量不能真实的反应实际故障偏差,如何降低跟踪误差的影响,提高滤波新息的准确度将有助于提升阶跃故障或者斜坡故障检测的性能[7]。一些学者相继提出了信号权重法、鲁棒估计策略和滑动窗口法等用于提高故障检测准确率和识别速度。ZIEBOLD 等[8]构建了基于载波噪声比的权重模型引入到扩展卡尔曼滤波估计过程中调整量测协方差矩阵,降低故障量测的影响以提高检测性能。陈含智等[9]采用滑动窗口法计算滤波新息,实时估计观测噪声方差矩阵,进而重构故障检测量,考虑了动态噪声对故障检测准确率的影响。ZHANG 等[10]在滑动窗口法基础上,引入鲁棒滤波估计理论对滤波增益矩阵进行自适应调节,进一步提高故障检测性能。上述方法都重在考虑观测噪声方差矩阵对于新息检验量的影响,通过提高观测噪声的准确度,进一步提升故障检测效果。然而,无论是快照法还是序贯法,在进行一致性检验中均假设观测残差或者新息服从卡方高斯分布来进行故障检测,这在列车实际运行环境中将面临一个重大的挑战。列车运行中观测信号受到电离层时延或多径干扰将不再服从高斯分布[11]。单纯地假设观测新息服从某一概率分布模型来检测是否发生故障并不能与时变的运行环境相匹配。因此,既有的故障检测算法在列车运行中会面临不可避免的性能水平下降问题,带来较大的安全隐患。除了基于统计分布的故障检测,基于密度的异常检测随着大规模数据挖掘的研究深入而逐渐受到研究人员广泛关注,局部离群因子(Local outlier factor,LOF)作为典型的密度异常检测方法,通过比较当前数据点与其近邻数据的密度差异来识别异常数据,不受数据分布不确定性问题的制约。在此思路下,本文提出了一种基于局部离群因子增强的故障检测方法,通过现场数据对所提方法进行验证分析,为时变卫星定位观测环境下的故障检测提供了新思路。
1 基于局部离群因子的卫星定位故障检测框架
1.1 系统框架
本文算法由数据感知、状态估计和故障检测3个部分组成。在数据感知模块,卫星接收机用于提供原始的观测伪距和列车运行过程中的星历数据,惯性导航系统用于感知列车的加速度和角速度信息,这2种定位传感器的感知信息将通过滤波算法用于估计列车位置。在信息融合模块,结合惯性导航方程得到的位置信息和卫星接收机提供的星历数据获取预测伪距,将其和卫星接收机的观测伪距联合共同构建量测方程,进一步通过扩展卡尔曼滤波进行状态估计,获取的估计误差将反馈给惯性导航系统定位结果。在进行状态估计前,卫星导航提供的观测信息首先需要通过故障检测模块进行检测,如果滤波新息的局部离群因子大于检验限值,则表明当前观测量受到运行环境因素的影响存在故障,需要重新更新量测方程后进行状态估计。具体框架如图1所示。
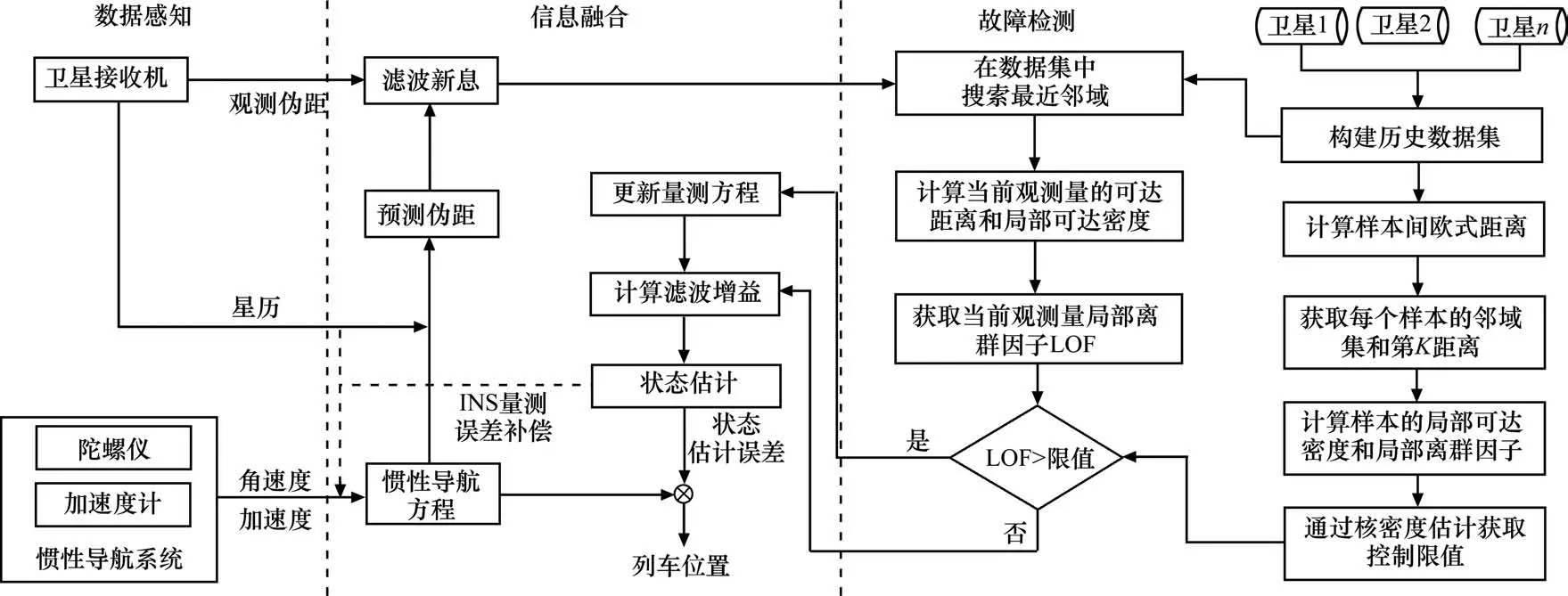
图1 算法框架图Fig.1 Framework of the proposed algorithm
1.2 状态估计模型
在信息融合中,需要首先构建组合系统的状态方程和量测方程。考虑卫星导航接收机钟差、钟漂误差和惯性导航系统陀螺仪和加速度计的量测误差等,设置17维的状态估计量,具体表示为
式中:(δφx,δφy,δφz)为地心地固坐标系下3 个方向姿态误差,(δvx,δvy,δvz) 为三轴速度误差,(δx,δy,δz)表示3 个方向位置误差,(εx,εy,εz)表示陀螺仪的三轴漂移误差,(γx,γy,γz)表示加速度计的三轴随机误差,(bclk,)为等效钟差距离误差和等效钟漂距离误差。
进一步地,将惯性导航系统误差方程与卫星导航系统误差方程结合,设计组合系统的状态方程为
Fk-1为状态转移矩阵,由k-1 时刻GNSS 和INS 的误差传播模型组成。wk-1为服从均值高斯分布的过程噪声,相应地协方差矩阵记作Qk。
进一步考虑卫星导航接收机的伪距观测量ρGNSS和惯性导航系统推算得到的预测伪距ρINS,确定观测矩阵为
组合系统的量测方程可以表示为
Hk表示组合系统的量测矩阵,vk表示服从零均值高斯分布的量测噪声,相应的协方差矩阵记作Rk。
利用当前时刻观测量和前一时刻惯性导航的状态预测能够估计当前时刻列车的状态信息,具体过程如下。
1) 状态一步预测:
2) 一步预测误差协方差矩阵:
3) 滤波增益矩阵:
4) 状态估计:
5) 误差协方差矩阵更新:
2 局部离群因子基本原理
局部离群因子方法通过衡量观测数据的局部密度来发现异常数据[12]。其赋予每个数据点一个表征其离群程度的因子,这个因子实质上反映了该数据对象与其特定邻域范围内其他数据对象之间的相对密度关系。通过衡量数据点的局部密度,寻找差异化最显著的点来识别异常数据。局部离群因子的一些重要基本概念如下。
定义1数据p的第K距离
数据集D中,数据点p和数据点q之间的距离表示为dis(p,q)。对于任意正整数N,数据p的第K距离记作Kdis(p),需满足下述2个条件:
1) 在数据集D中至少有除p点之外的N个数据点Q,满足dis(p,Q)≤dis(p,q);
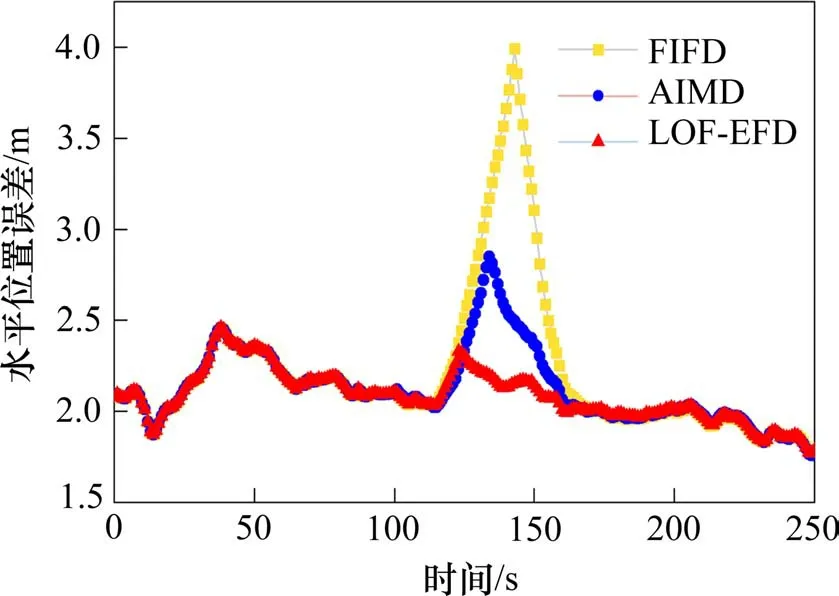
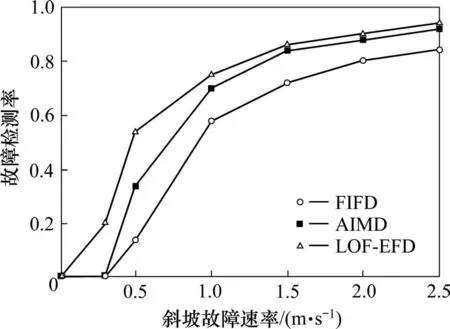
2) 在数据集D中至多有除p点之外的N-1 个数据点Q,满足dis(p,Q) 定义2数据p的第K距离邻域 数据p的第K距离邻域是指数据集内所有与p的距离不超过Kdis(p)的数据对象的集合,表示为: 定义3可达距离 可达距离是用来度量2 个数据点之间的距离,数据点q到点p的可达距离为: 定义4局部可达密度 数据点p的局部可达密度是K距离邻域内数据点到p的平均可达距离的倒数,邻域内数据点总数记作M,则局部可达密度可表示为: 局部可达密度反应了限定邻近空间内数据点的聚合程度,如果一个数据与周围数据有着显著差异,则相同的K值下,其K距离邻域的覆盖范围较广且涵盖的数据较少。异常数据点p落在其邻域数据点第K距离邻域内的可能性较小,即对于p的K距离邻域内的数据点q而言,数据点q到p的可达距离reach_dis(p,q)取两点之间真实距离的可能性远远大于q的第K距离。如果数据点p无显著性偏差,则reach_dis(p,q)取q的第K距离可能性更大。由此可知,一个潜在异常的数据点其可达距离之和数值较大,计算得到的局部可达密度较小。 定义5局部离群因子 进一步,可根据数据点p及其邻域点的局部可达密度计算p的局部离群因子 对于一个具有M个邻域点的数据点p而言,若p存在偏差,计算得到的局部可达密度较小,而其邻域点的可达距离整体差异性较小,计算得到的局部可达密度较大,因此,偏差数据的局部离群因子较大。相反,如果p与周围数据点差异性较小,则不同数据点之间的局部可达距离之和没有显著变化,局部密度较为均匀,由此得到的局部离群因子比较接近。 基于局部离群因子增强的故障检测法(Local Outlier Factor-based Enhanced Fault Detection,LOFEFD)是根据密度异常检测思想所设计,其不依赖于数据集的任何先验知识,无需提前假定数据集的分布情况,聚焦于数据点与其邻域数据的密度分布情况。而传统的基于滤波理论的故障检测是建立在统计分布理论基础上,其故障检测准确率受到假定数据分布模型的约束,当预设分布模型不合理时,将会发生严重的漏检。 LOF-EFD 主要划分为建立历史数据集和故障检测2个部分。建立历史数据集的目的是通过分析正常条件下卫星信号的观测数据来获取控制限。卫星观测数据质量受到卫星仰角、载噪比等多种因素的影响[13]。较高的仰角不易受到周围建筑等的遮挡,而较低的仰角则容易受到多径效应的影响导致量测质量下降。载噪比从信号接收的强度度量所观测数据的质量情况,受到环境干扰的观测信号载噪比总是低于正常观测条件中的。因此,在构建历史数据集的过程中,通过每一颗卫星的仰角和载噪比衡量对应时刻的数据质量,选择未受到外界干扰的卫星观测数据构建检验统计量。大多数情况下,当观测卫星的仰角低于20°并且载噪比低于35 dB-Hz 时,其数据质量严重下降,不再用于定位解算过程[14]。 因此,利用状态估计过程中满足约束条件的卫星观测量构建历史数据集: 其中,n为正整数,表示数据集样本量,yn由新息和新息协方差矩阵组成,可以表示为: 式中:Δzk为系统实际观测量与滤波器状态预测值之差,即新息,Sk为新息协方差矩阵。进一步,通过计算每一个数据样本与其他数据之间的欧式距离Ed(ya,yb),a,b=1,2,…,n,将X映射到距离数据空间Οn×n。 由定义1 和定义2 可知,一个样本的第K距离值可以看作是其邻域的最大展开半径。按距离从小到大重新排列数据空间On×n,根据设置的邻域范围K值,确定每个时刻样本点的近邻点,将其近邻点组成的集合记作N(y)。第K+1 个近邻点与样本点yi的欧氏距离即为yi的第K距离,记作Kdis(yi)。 2 个样本点并不总是互为近邻点,需结合距离数据空间和每个样本点的第K距离,才能够得到邻域点到yi的可达距离。定义近邻域点ym∊N(y)到yi的可达距离为: 通过遍历集合N(y),能够得到yi对应的局部可达密度: 利用每个样本点的局部可达密度,根据公式(13)可以计算得到历史数据集中样本的局部离群因子,记作集合Г{LOF(y1) LOF(y2) … LOF(yn)}。局部离群因子仅仅是反应了每个样本点的离群程度,为实现故障检测的目的,利用核密度估计方法估计正常样本局部离群因子的控制限。对于给定的集合Г,变量y的概率密度函数如下: 其中,G是核函数,通常采用的是高斯核函数。h为平滑参数。 对于给定的误警率,取常用值0.01[5],置信限值TLOF能够通过如下得到 故障检测过程主要是对当前观测量进行分析,通过与控制限比较判断其是否受到不确定因素干扰,而存在较大偏差或异常。对于一个新样本点ynew而言,其与历史数据集各个样本之间的欧氏距离空间需要首先被构建,进而通过设置的最大邻域值寻找相应的近邻域集Ynew,根据式(22)计算近邻域点yold∊Ynew与ynew之间的可达距离: 利用式(12)得到当前新数据点的局部可达密度,进一步可得到当前数据点的局部离群因子: 通过比较当前局部离群因子与控制限值的大小,能够判断是否存在故障。如果LOF(ynew) 本文采用西部低密度铁路列车真实行驶数据对所提出的故障检测算法进行测试和验证。车上安装有诺瓦泰SPAN-FSAS 分体式组合导航定位系统,用于采集卫星原始观测量和惯性导航数据,并提供高精度的真实位置参考。列车行驶区段位于“日喀则―拉萨”,行驶速度为107~116 km/h,行驶过程中可见卫星数共8 颗,水平精度因子在0.6左右。实验设备安装情况如图2所示。 图2 实验设备Fig.2 Experimental devices 用于实验验证的数据时间长度为500 s,参与解算的卫星编号分别为10,14,18,22,25,26,31 和32。为充分验证本文算法在不同故障类型下的性能,将采集数据划分为2 部分,0~250 s 用于构建历史数据集,250~500 s用于监测是否存在故障数据。针对典型故障类型,在检测数据的不同时段分别加入不同大小的阶跃故障和斜坡故障,并与基于滤波新息的故障检测算法(Filter innovation-based fault detection,FIFD)[15]和自主完好性监测外推法 (Autonomous Integrity Monitored Extrapolation,AIME)[16]进行比较。 为验证不同算法在阶跃故障下的检测性能,在101~150 s 向可见卫星G32 的伪距观测中添加15 m的阶跃故障,图3所示为阶跃故障场景下不同算法的检测结果。考虑到基于局部离群因子增强的故障检测法是架构于K最近邻思想,邻域参数的选择影响着数据点的相对密度表征程度。为了选择合适的邻域值,首先选择20,30,40 和50 不同邻域值进行故障检测比较。从图3中可以发现,在故障检测区域,不同邻域值下检验统计量均超过了检验阈值。对于一个较小的邻域值而言,在无故障区域,会发生一定程度的误检。而随着邻域值增大40,无故障时间段正常数据的局部密度趋于稳定,当邻域值继续增大到50 时,并无明显变化。因此,选择40 作为邻域范围进一步分析算法性能。在故障检测区域,FIFD 算法的检验统计量一直未超过检测阈值,AIME 算法仅有部分时刻检验统计量超过了检测阈值,故障检测率为38%,相比上述2 种算法,本文所提算法分别提高了100%和62%,具备更强的检测能力。 图3 不同算法的故障检验量Fig.3 Fault detection statistics with different methods 进一步分析故障检测能力与位置估计之间的影响,图4显示了15 m 故障偏差作用下3种算法的水平位置误差变化情况。从图中可知,由于FIFD算法未能及时检测出故障卫星,在故障发生期间其水平位置误差随着故障持续时间而不断增大,均方根误差为3.24 m。AIME 算法在故障注入初期能够检测出故障,剔除故障量测的影响,但随着故障检测量低于检验阈值,定位性能也随之发生明显的劣化,位置估计误差逐渐缓慢增大,均方根误差为2.54 m。相较于FIFD 和AIME,由于检测能力带来的差异,LOF-EFD 算法的均方根误差为2.07 m,分别降低了36.1%和18.5%。对故障发生期间定位结果进行统计分析,结果如表1所示。 表1 15 m阶跃故障下不同算法定位精度Table 1 Positioning accuracy of different methods under step faults (15 m) 图4 水平位置误差变化情况Fig.4 Variation of horizontal position error 为探究算法对不同阶跃故障的检测敏感度,向可见卫星G32的伪距观测中依次注入9~27 m 的阶跃偏差,每种算法的故障检测率变化情况如图5所示。从图中可知,LOF-EFD 能够识别更微小的故障偏差,当伪距偏差增加到9 m 时,便能够相继识别出故障,而AIME 和FIFD 算法需要在伪距偏差增加到13 m和21 m时才能识别出来。 图5 不同阶跃故障下故障检测率对比Fig.5 Comparison of fault detection rate under different step faults 为验证本文算法在斜坡故障下的检测性能,在101~150 s 内向可见卫星G32 的伪距中添加以0.5 m/s速率增长的缓变斜坡故障,3 种算法的检验统计量如图6 所示,阈值1 为对照算法获得的检验阈值,阈值2 为LOF-EFD 获得的阈值。故障发生期间,随着缓变故障的不断增大,3 种算法的检验统计量均逐渐上升,并在故障结束前超过了检验阈值,但每种算法检测到故障的时间延迟不同。局部离群因子增强的故障检测法计算得到的检验统计量在124 s 超过检验阈值,随后一直保持在阈值之上,时延为23 s;AIME算法在第135 s首次识别出故障,相比LOF-EFD 滞后了11 s,故障检测率为34%,而FIFD 算法在临近故障发生期结束,即第144 s 才开始识别出来故障,相比所提的算法延后了20 s,故障检测率仅为14%。与FIFD 和AIME 相比,LOF-EFD 方法分别提升了40%和20%,故障检测率达到了54%,能够更加及时的识别出来缓变故障。 图6 不同算法的故障检测量Fig.6 Fault detection statistics with different methods 图7进一步给出了在该种斜坡速率故障条件下3 种算法的定位误差变化情况。从图中可知,在故障发生初期由于故障偏差较小,对于定位估计没有产生影响,随着故障的不断增大,3 种算法得到的水平位置误差都开始呈现上升趋势,由于LOFEFD 能够较早的检测到故障量测,其定位误差在短暂的增大后下降到正常情况;而AIME 和FIFD算法的定位误差受到斜坡故障的影响时间较为持久,分别在135 s 和144 s 达到最大定位误差2.84 m和4 m。对3 种算法在故障发生期间水平位置误差进行统计分析得,LOF-EFD,AIME 和FIFD 的均方根误差分别为2.14,2.34 和2.79 m,相比FIFD和AIME 方法,LOF-EFD 在均方根误差上分别降低了28.6%和9%。故障发生期间定位统计分析结果具体如表2所示。 表2 斜坡故障下不同算法定位精度Table 2 Positioning accuracy of different methods under ramp faults 图7 水平位置误差变化Fig.7 Variation of horizontal position error 为探究算法对不同速率斜坡故障的检测敏感度,向可见卫星G32 的伪距观测中依次注入0.5,1,1.5,2 和2.5 m/s 的斜坡故障,每种算法的故障检测率变化情况如图8所示。从图中可知,相比较另外2 种对比算法,LOF-EFD 具有更高的检测率,且能够识别更小速率的斜坡故障偏差,具备更强的故障检测性能。 图8 不同斜坡速率故障下故障检测率对比Fig.8 Comparison of fault detection rate under ramp rate fault 1) 考虑列车卫星定位故障检测阶段通常假设滤波新息服从确定分布进行一致性检验,本文在滤波新息故障检测法的基础上,引入密度异常检测思想,构造了基于局部离群因子增强的故障检测方法,消除了传统检验统计量对数据需满足卡方高斯分布的假设要求,突破了确定统计分布假设带来的性能约束。 2) 所提算法对于阶跃故障和斜坡故障2种不同类型故障均具有较强的敏感性,能够检测出较小的故障。在阶跃故障中,当故障偏差超过9 m 时,本文算法可以相继识别出来,而FIFD 和AIME 方法需要在伪距偏差增加到13 m 和21 m 时才能开始识别出来。在0.5 m/s 速率的斜坡故障中,相比FIFD 和AIME 方法,故障检测延迟时间分别缩短了20 s和11 s。 3) 所述方法重点聚焦于卫星导航信号在受外界环境干扰条件下发生异常时的故障检测,尚未考虑惯性导航系统故障时对组合定位系统状态估计的影响。为此,后续工作将进一步探究组合定位系统各导航定位源的故障机理,对故障来源进行有效区分、识别和排除。3 基于局部离群因子增强的故障检测方法
4 验证与分析

4.1 阶跃故障下检测性能分析
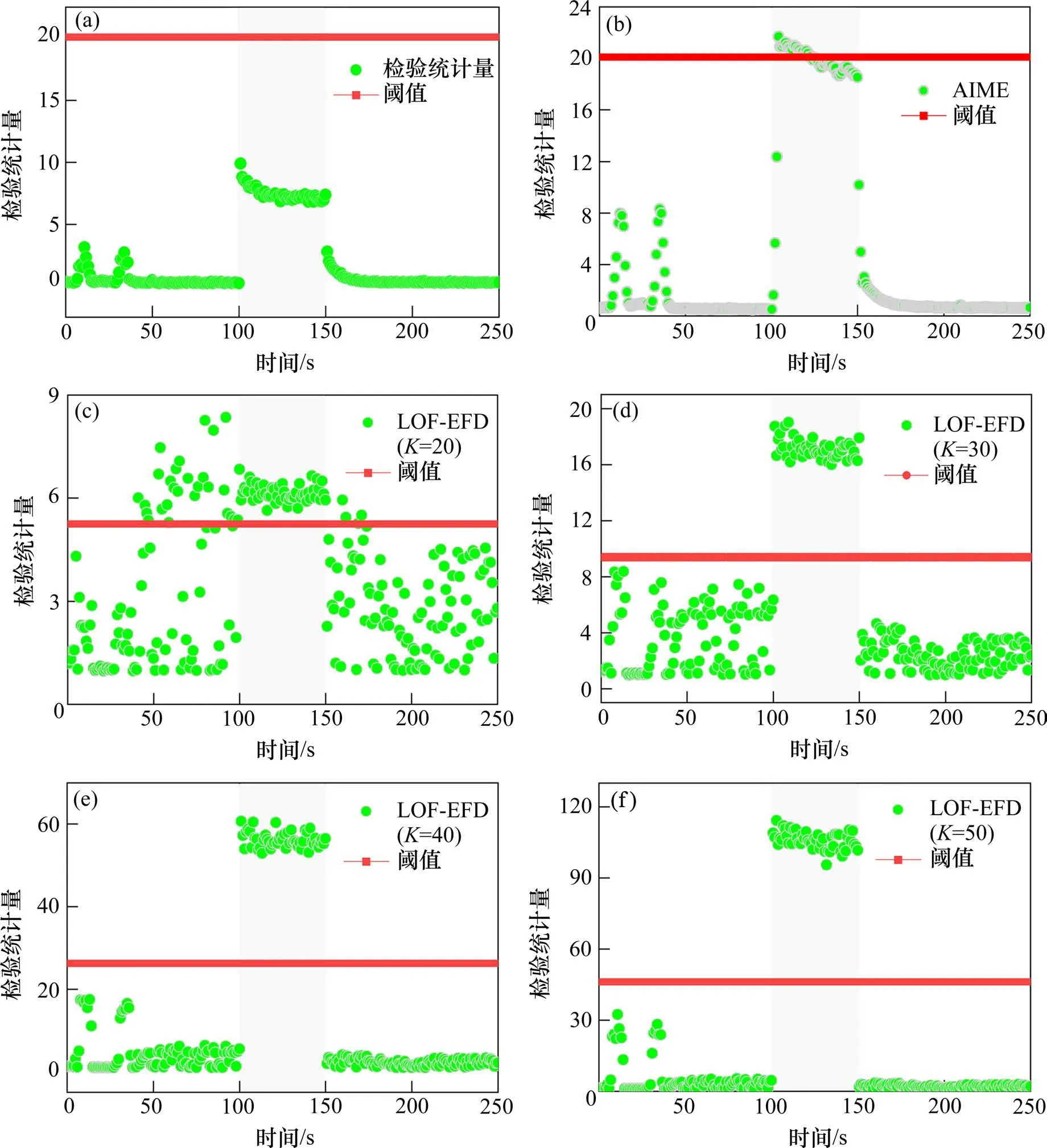
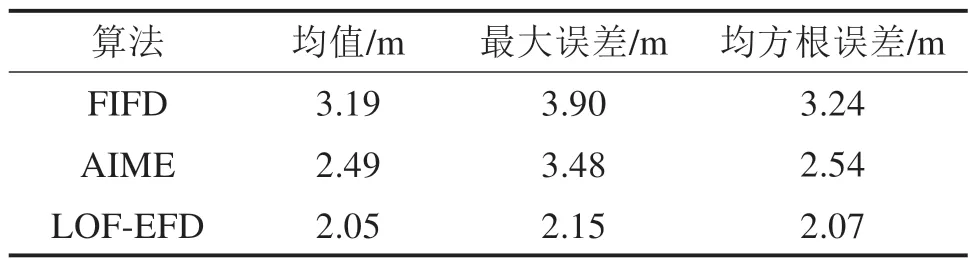


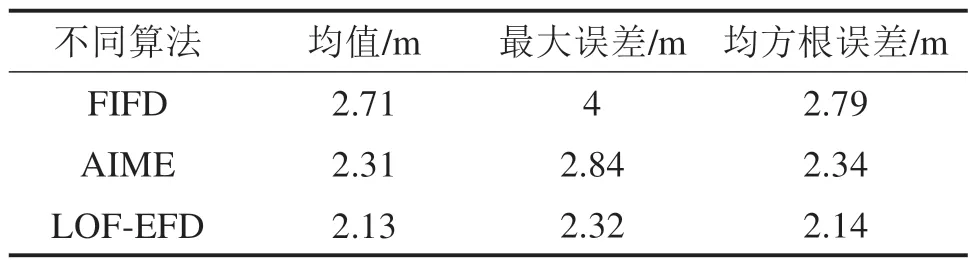
4.2 斜坡故障下检测性能分析

5 结论

