基于新型跟踪微分器的磁浮车悬浮控制算法研究

张文进，林志坚，张睿扬，龙志强，顾秋明，张和洪

(1.福州大学 物理与信息工程学院，福建 福州 350000；2.南京理工大学 机械工程学院，江苏 南京 210094；3.国防科技大学 智能科学学院，湖南 长沙 410073；4.乐嘉建设工程有限公司，福建 福州 350000；5.福州大学 计算机与大数据学院/软件学院，福建 福州 350000)

磁浮列车作为一种新型轨道交通工具，改变了传统铁路的轮轨接触支承与驱动的方式，通过电磁力使车辆悬浮并驱动列车前进，它与传统轮轨列车系统相比，具有噪声低、摩擦损耗小、维护成本低和爬坡能力强等优势，是一种具有良好发展前景的交通工具[1]。磁悬浮技术发源于德国，之后中国、日本、韩国和加拿大等国家也相继开展了磁悬浮轨道交通技术的研发工作，而中国在此方面发展较快，已从试验研究阶段向试验运行、商业化运行模式转变，目前已有的中低速磁悬浮运营线有北京磁浮S1线和长沙磁浮线[2]。悬浮控制技术是磁浮列车的关键和核心技术之一，悬浮控制系统性能的好坏直接影响磁浮列车的稳定性、安全性和舒适性[3]。其中，PID 控制算法由于设计简单、鲁棒性强、调节方便等特点常被用于磁浮车控制中[4-5]。然而，磁浮列车间隙传感器中常常存在随机噪声，PID 控制器的微分环节是直接采用数值差分法[6]对间隙信号提取相应的速度信号，这会引起噪声放大效应，进而导致悬浮不稳甚至导致列车与轨道吸死等状况。为了解决这一问题，研究人员提出了许多不同的微分器设计方法来对含噪声信号进行合理的滤波与微分提取，包括线性时间微分跟踪器[7]、基于高增益观测器[8]、精确鲁棒微分器[9-10]，有限时间收敛微分器[11]等。其中HAN[12]提出了跟踪微分器的概念，其不但能从带随机噪声的输入信号中有效跟踪原始信号，还能合理地提取微分信号。韩京清等[13-14]对文献[12]中的fhan-TD 的频域特性以及收敛性进行分析，证明了该跟踪微分器在信号跟踪滤波以及微分获取方面具有良好效果。现阶段针对跟踪微分器的研究与设计被应用到不同领域中，LIU 等[15-16]分别设计了自适应跟踪微分器及高精度跟踪微分器，并在机电系统和磁浮车信号检测系统中得到验证。张文跃等[17-18]分别设计了NHS-TD 与THAN-TD，在消除磁浮车悬浮传感器过轨道接缝的信号畸变上取得良好效果。跟踪微分器算法中，控制综合函数的形式与特点对滤波特性、跟踪相位滞后、微分信号估计准确度方面起决定性作用，因此如何设计恰当的控制综合函数被作为重点研究内容。韩京清等[19]通过状态反步法给出了跟踪微分器控制综合函数的一般形式，但是函数中包含非线性的根号运算，在离散化的数字控制系统中计算量大，对于控制算法具有一定的复杂性。针对此问题，谢云德等[20-21]通过寻找最速控制取非极值的线性区边界特征点，构造了简单的线性函数，避开了复杂的根号运算，提出了易于实现的FTD，但是该TD 参数较多，整定较为繁琐。ZHANG 等[22]根据初始点位置选取相应控制量，推导出对应的边界曲线以及特征曲线，采用线性化准则，提出结构简单的跟踪微分器，并验证了该TD 具有良好的微分及跟踪性能，但并没有给出具体的TD 表达式，对于工程实现具有一定的复杂度。本文将从控制综合函数入手，提出一种新型简易离散跟踪微分器，用状态反步法确定最速离散二阶系统的线性区域边界曲线以及控制特征曲线，并确定可达区与线性区的控制量，构造出统一的边界曲线表达式，不依赖边界的变换，使得控制综合函数形式简化，给出新型TD 的具体表达式。所提出的简易跟踪微分器算法中不含非线性运算，适用范围更加广泛。通过仿真和试验验证了所提跟踪微分器的良好特性，为工程实现提供了一种行之有效的方法。

1 磁浮车悬浮控制系统

1.1 悬浮系统模型建立

磁浮列车悬浮控制单元由相应的轨道和电磁铁组成，通过实时控制电磁铁线圈的电流来提供平衡系统重力的电磁力以保证一定的悬浮间隙。其中，悬浮控制系统基本原理如图1所示，其物理机理模型是以磁浮车动力学方程和电学、力学关联方程为基础建立起来的。由电磁理论可知，通电电磁铁线圈绕组能够产生方向竖直向上，大小随电流变化而变化的电磁吸力，磁浮车依靠电磁吸力以设定间隙悬浮于轨道之上。如图1所示，磁浮车体单个转向架包含4个悬浮控制单元，各点呈90 度角分布，系统借助空气弹簧实现机械解耦进而使得4个悬浮单元之间相互独立，故单点悬浮控制系统可作为磁悬浮系统的基本单元，分析其动态模型及特性具有一般性。

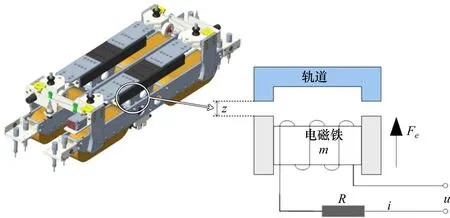
图1 磁浮车悬浮系统结构图Fig.1 Structure diagram of the maglev suspension system

如图1所示，以向下为正方向，电磁铁的动力学方程为：

=mg-Fe，磁力Fe为：

其中：μ0表示真空磁导率；N表示电磁铁线圈的匝数；A表示电磁线圈的有效极面积。由式(1)可知电磁力Fe与间隙z是非线性的反比关系，表明悬浮系统是一个非线性不稳定系统。

电磁铁电压电流方程：

其中：L为电磁铁线圈等效电感，电感的等效表达式为，代入(3)式可得：

合并式(2)与式(4)得到单点悬浮系统模型：

由于控制系统的设计是针对线性化以后的系统，故只考虑电磁铁在平衡后附近的特性，在电磁铁运动的小范围内，设电感为常量，根据式(5)创建3阶状态空间方程：

其中：y为悬浮系统悬浮间隙的导数。通过采用快速电流环技术，将电磁铁两端的电流电压关系等效为比例关系：u=iRk，Rk是电流环校正后的等效电阻。将比例系数代入式(6)可降阶为一个2 阶系统：

上式中：x1为间隙位置信号，x2为位置微分即速度信号。容易证明，该2阶系统是能控系统，为之后设计反馈控制器打下基础。根据磁浮列车数学模型，悬浮控制系统参数如表1所示。

表1 磁浮车系统参数Table 1 System parameters of the maglev train

1.2 磁浮车悬浮系统控制器

本文采取当前相对成熟且工程界广泛应用的PID 算法用作悬浮系统控制器，其设计简单，鲁棒性强。PID 中的微分环节若使用数值差分法只能近似得到间隙信号的微分信号且极易造成噪声放大问题。经过真车实际运行工况得知输出间隙通道噪声强度在65～75 dB 之间，受到噪声影响会使相关的悬浮点上下抖动甚至吸附在轨道上，而在间隙输出端加入跟踪微分器能够对带噪声信号进行有效的跟踪滤波，进而反馈回悬浮系统控制器，控制磁浮车稳定悬浮。

在输出间隙通道加入跟踪微分器之后，悬浮系统的反馈控制器结构如图2 所示，v0为输入设定间隙信号，yout为系统输出间隙信号，x1为跟踪滤波信号，其与v0之差记作误差信号e1，为间隙误差的微分信号，为间隙误差积分信号，η为系统中的量测噪声。控制量由PID控制器输出，作用到由电流环与位置环组成的被控对象中，最终表现为悬浮系统输出间隙信号。其中设计有效的跟踪微分器算法对间隙传感器输出信号进行处理是构造磁浮列车悬浮反馈控制器结构的核心与关键。

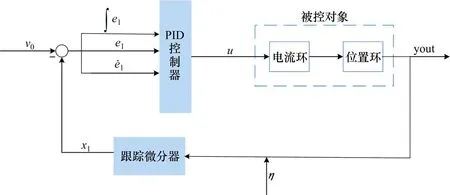
图2 磁浮车单点悬浮控制框图Fig.2 Single point suspension control block diagram of the maglev train

2 新型跟踪微分器设计

韩京清跟踪微分器离散形式[23](即fhan-TD)中含有根号运算，增加了运算复杂度，不利于系统实现；此外，实际系统中一般是数字控制系统，需采用离散化的形式，跟踪微分器算法中选取合适的边界曲线及不同控制区域的控制量会影响甚至决定跟踪性能及微分品质。为此，本文提出一种综合控制函数，该算法采用可变换的边界层开关曲线，能够根据不同情况恰当修改不同区域控制量，从而获得跟踪精度更好、抗噪声能力更强的新型离散跟踪微分器。

2.1 构造边界曲线

对于双积分连续串联最速系统：

其离散化可以表示为：

其中：j=0，1，2，…，k。若系统经过k+1步，到达相平面的原点，即x(k+1)=0，可以推出起始点必须满足：

由最优控制理论[23]可得，最速系统(8)的控制策略是一种开关曲线(见图3)：

图3 开关曲线Г以及边界曲线ГA与ГBFig.3 Switching curve Гand boundary curve ГA and ГB

通过Lyapunov 函数可以证明系统(8)所有最速轨线都将在有限时间内到达原点。

相平面上的点在开关曲线的上方，控制量u取-r；位于开关曲线下方时，控制量u取+r。到达开关曲线时，控制量切换符号，在离散条件下，控制量切换的过程发生在一个线性区内，记为Ω，控制量在该区域内按线性标准变化。显然这个线性区一定在开关曲线附近，因此要寻找线性区的边界曲线以此判定非线性区以及线性区从而取不同的最优控制量。

由文献[14]可知，边界线有2 条，一条线上控制量均取-r或+r到达原点，将该类型初始点集合记为{a+k}，{a-k}，并构成曲线ГA，其中点集合{a+k}所在曲线为ГA+，点集合{a-k}所在曲线为ГA-；另一条曲线上的点集合{b-k}，{b+k}。首先取-r(+r)，然后全部取+r(-r)到达原点，构成曲线ГB，其中点集合{b+k}所在曲线为ГB+，点集合{b-k}所在曲线为ГB-。

对于曲线ГA+，初始点在第k+1 步到达原点x(k+1)=0，此时有u(j)=+r,j=0,1,2,…,k，由 式(11)可得：

因此整条曲线ГB(见图3)可以表示为：

根据方程(11)，(14)和(15)，可构造出统一的边界曲线表达式如下所示：

其中λ为变换因子，根据式(16)可得：

当λ=0 时，即为曲线ГA，当λ=1 时，即为曲线ГB，可根据初始点的区域灵活选取边界曲线，进而寻求最优控制量。

2.2 构造控制综合函数

相平面一点M(x1,x2)若在区域Ω 内并且2 步以内可以到达原点，则初始点x(0)以及相关控制量满足方程(9)，使得：

求解上式得到：

2 步内可以到达原点的点集合位于2 条平行线x1+hx2=h2r,x1+hx2=-h2r以及另外2 条平行线x1+2hx2=h2r,x1+2hx2=-h2r围成的区域，记作此区域为Ωr；

图4 2步可达区示意图Fig.4 Schematic diagram of two-step reacheable region

当M(x1,x2)在可达区Ωr内，取控制量u=(x1+2hx2)；当M(x1,x2)位于线性区Ω 内但不在可达区Ωr时，取控制量u=-r∙sgn(x2)∙(1-2λ)，λ取式(17)；当M(x1,x2)位于线性区之外时：在第一象限或第三象限(即x1x2>0)时，控制量u取u=-r∙sgn(x1+hx2)；在曲线ГA-以及ГB+上方时，控制量取u=-r；在曲线ГA+以及ГB-下方时，控制量取u=+r。根据以上分析，构造本文所提变边界层控制综合函数表达式为：

最终跟踪微分器(记为fst-TD)的表达式为：

其中：r为速度因子，代表跟踪速度；c0为滤波因子，代表滤波程度。

3 仿真及试验分析

3.1 数值仿真

为了验证本研究所提fst-TD对于信号跟踪滤波及微分提取的有效性，与fhan-TD 进行对比。分别选取输入信号v(t)=sin(t)+η(t)，η(t)为60 dB 的高斯白噪声；v(t)=sgn(sin(t))+γ(t)，γ(t)为强度0.01 均匀分布的白噪声。仿真采样步长与真车采样步长一致：h=0.001，滤波因子c0与速度因子r均通过大量调试比较，得到较好的仿真结果。

通过图5和图6以及表2对比分析发现，fst-TD与fhan-TD 都可以有效地跟踪原始输入信号，但前者的跟踪相位滞后及滤波性能均优于后者：当输入信号为带噪声正弦信号时，Nf减小0.000 9，Lf减小0.044 8，表明滤波效果提升37.5%，相位滞后减小5.04%；当输入信号为带噪声方波信号时，Nf减小0.002 1，Lf减小0.084 6，表明滤波效果提升33.87%，相位滞后减少30.34%。

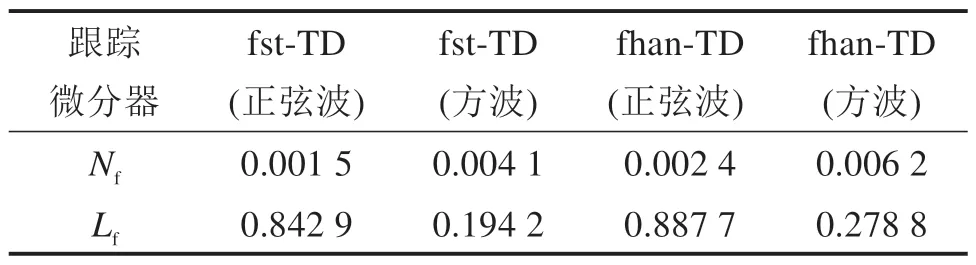
表2 输入信号为带噪声方波及带噪声正弦波情况下fst-TD与fhan-TD对比Table 2 Comparisons of fst-TD and fhan-TD when the input signal is square wave with noise and sine wave with noise

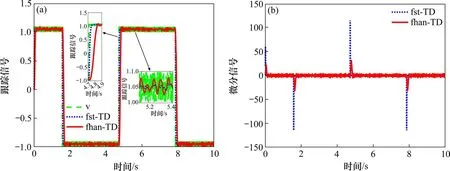
图6 输入信号为v(t)=sgn(sin(t))+γ(t)的跟踪滤波及微分对比Fig.6 Comparisons of tracking filtering and differentiation when the input signal is v(t)=sgn(sin(t))+γ(t)

3.2 磁浮小车实验测试

为验证所提出的跟踪微分器算法及其相应的悬浮反馈控制器，本部分内容将前述所提的控制结构应用到实验室磁浮小车平台进行实验测试。

图7为实验室磁浮小车测试平台，该磁浮小车参考国内中低速磁浮列车结构，整车由车体、转向架、轨道和4个悬浮点组成。每个悬浮点包括电磁铁、间隙传感器、电流传感器、加速度传感器、涡流传感器、信号调理电路、模拟量控制模块和功放模块。根据该磁浮小车实际运行工况，传感器采集相应的间隙信号以及电压信号显示在上位机中，用作实验数据进行分析。

图7 磁浮小车实验平台Fig.7 Maglev train experiment platform

由图8(a)可知，在磁浮小车起浮阶段，基于PIDfhan-TD 控制器的悬浮间隙超调量为8.554 7%，调节时间为0.253 s，而基于PID-fst-TD控制器的悬浮间隙为1.981 5%，较前者减少6.573 2%；调节时间为0.152 s，较前者减少0.11 s。由图8(b)能够看出，基于PID-fst-TD 控制器的悬浮速度信号(即间隙信号的微分信号)进入平稳运行的时间更短，震荡幅度更小，表明基于PID-fst-TD的控制器能够控制磁浮车悬浮更加稳定。

图8 磁浮车起浮阶段不同悬浮反馈控制器对比Fig.8 Comparisons of different suspension feedback controllers in the suspension stage of the maglev train

图9为磁浮小车运行过程中，间隙传感器存在不同强度噪声情况下不同跟踪微分器的滤波效果对比。为更加直观对比滤波性能，引入以下性能指标进行定量分析：平方误差积分准则(ISE)为，时间乘绝对误差积分准则(ITAE)为为输出间隙与额定间隙的误差。其中ISE 越小代表整体振荡越小，ITAE 越小代表整体误差越小，输出间隙曲线更加贴近设定值。

图9 不同噪声强度下悬浮系统输出间隙滤波对比Fig.9 Comparisons of output gap filtering of suspension system under different noise intensity

从图9可以看出，在磁浮车运行过程中受随机噪声的影响下，单纯依靠PID控制器进行控制会造成极大的悬浮间隙上下波动，无法使磁浮车稳定悬浮，尤其是当噪声强度较大时(图9(a))，磁浮车甚至会发生吸死状况。在输出通道加入跟踪微分器构成悬浮反馈控制器后，可以看到2 种TD 均能对带随机噪声的间隙信号进行有效滤波，使悬浮间隙的浮动范围极大减小。而基于本文设计的fst-TD 在工况a 及工况b 下的滤波表现均优于fhan-TD，通过表3 可以看出在工况a 下，ISE 减少了1.853 7×10-7，ITAE 减少了0.001 1；在工况b 下，ISE 减少了1.107×10-8，ITAE 减少了2.393 6×10-4。表明在悬浮系统输出端加入fst-TD后，对噪声的抑制能力更强，磁浮小车悬浮更加平稳。

4 结论

1) 提出一种简易形式的新型跟踪微分器算法，其控制综合函数中不含有非线性运算，可灵活变换边界曲线，形式简单易于实现，相比于已有其他算法，数值仿真表明所提算法具有优秀的信号跟踪及微分提取能力，实验测试表明所提算法对于悬浮控制系统输出通道中的随机噪声具有良好的滤波效果，并且有较好的相位品质，能够满足磁浮车在噪声影响下稳定悬浮的需求。

2) 搭建PID 与TD 结合的悬浮反馈控制器，试验结果表明PID-fst-TD 相比于PID-fhan-TD，在控制磁浮小车起浮过程中具有较小的超调量以及较小幅度的振荡，并且控制磁浮小车进入平稳运行阶段的时间更短。该反馈控制架构为磁浮车悬浮控制器的设计提供了一种新思路。