弓网关系缩比模型设计方法研究

刘文正，伊金浩，张坚，李鑫，黄朝阳

(1.北京交通大学 电气工程学院，北京 100044；2.中铁工程设计咨询集团有限公司，北京 100055；3.长江师范学院 机器人工程学院，重庆 408100；4.中车青岛四方机车车辆股份有限公司 技术中心，山东 青岛 266111)

目前，国内外高速铁路运行速度已达到300 km/h以上，在京沪线开通前进行的整车实验速度达到486.1 km/h，法国实验列车速度甚至高达574.8 km/h[1]。随着列车运行速度的提高，在气动激扰及轮轨振动的影响下，受电弓振动和接触线波动加剧，弓网受流质量变差，弓网离线电弧频发[2-3]。而且，经前期研究发现，弓网接触力及离线特性的变化直接受接触网线索张力、吊弦位置等参数的影响[4-5]。在实际线路中，受实际情况或场地因素的影响，难以改变接触网线索张力及吊弦布置，分析接触力与接触网线索张力及吊弦布置等因素间的关系。为了分析各影响因素对弓网关系的影响，很多学者进行了诸多努力。一方面，MASSAT 等[6-7]采用仿真研究的方法，分析接触力与弓网结构参数、设计参数等众多因素的关系。另一方面，陈程等[8-9]分析了离线电弧与运行速度、弓网参数间的关系。但是，离线电弧还受连续变化的交流工频电压、连续变化的弓网离线间距及其联合作用的影响。由于目前难以基于实际线路获得连续变化的离线间距，如何分析动态因素对离线电弧或者接触力的影响成为亟待解决的问题之一。缩比实验平台具有造价偏低，占地面积小，比较适合弓网关系研究。缩比模型设计是搭建缩比实验平台的核心。因此，本文提出基于缩比平台进行弓网受流质量研究的方法。基于相似理论[10-12]，推导原模型与缩比模型之间的关系，对缩比模型结构参数、载荷大小、边界条件等参量进行计算，得到各关键物理量的缩比系数。关于缩比模型，MANABE 等[13-14]针对复链形悬挂接触网/受电弓系统设计了关于速度缩比的缩比模型，分析运行速度与弓网受流质量间的关系。但是，该模型只是对速度进行了缩比，只能研究实际线路上无法实现的超高速度对弓网受流质量的影响，无法分析结构参数对弓网关系的影响。为了进行弓网关系实验研究，本文以几何相似和几何不相似理论为核心，以简单链形悬挂接触网为主要研究载体，提出了适用于高速铁路弓网关系研究的缩比模型设计方法，用以构建缩比实验平台。然后，在此分析的基础上，基于仿真软件，建立弓网缩比模型，验证缩比模型的正确性。最后，从静态和动态角度对缩比模型的合理性进行验证。

1 弓网模型系统参数相似关系推导

1.1 仿真模型及相似理论

本文基于有限元仿真软件MSC.Marc 建立了弓网模型，模拟弓网耦合运动系统[15-16]。采用EN50318对本文建模方法进行了验证[17]。接触网和受电弓参数如图1(a)所示，仿真模型如图1(b)所示。

图1 接触网与受电弓模型Fig.1 Model of catenary -pantograph

模型中，接触线单元的振动方程为：

其中：m为接触线单元质量；E为接触线弹性模量；I为接触线截面惯性矩；T为接触线张力；P为弓网接触力；ks为吊弦的弹性常数；v为列车运行速度；yc为接触线各质点的垂向振动位移；x为受电弓以速度v，运行t时间后的沿z方向的位移。

受电弓的振动方程为：

其中：M为受电弓各部分的等效质量矩阵；C为等效阻尼矩阵；K为等效刚度矩阵；F为受电弓所受外力，F=[P，P0]T，P0为施加的静态抬升力，P为弓网间的接触力；yp为受电弓的垂向振动位移。

1.2 几何相似模型相似关系的推导

为了确保弓网关系研究的准确性，基于相似理论，对全尺寸弓网模型的关键结构参数进行缩比计算。为了实现实验平台的线路缩比，本文将模型尺寸分为水平尺寸和垂向尺寸，分别进行缩比[18]。其中，水平尺寸的缩比系数与垂向尺寸缩比系数相同时，为几何相似的缩比模型。水平尺寸的缩比系数与垂向尺寸缩比系数不相同时，为几何不相似的缩比模型；几何不相似模型仿真结果的误差虽然比完全相似模型略大，但有利于进一步实现速度缩比。为了进一步验证缩比系数的准确性，采用Pearson 法计算原模型与缩比模型的相关系数，相关系数越接近1，说明两模型的一致性越好。

1) 缩比模型推导

缩比模型采用长度[L]、质量[M]、时间[T]3个力学基本量纲为基本物理量，基于基本物理量可以导出其他物理量。根据1.1 节式(1)和式(2)可知，弓网关系实验研究涉及到的物理量包括弹性模量E，单位长度重量q，线密度ρ，长度L，材料截面积S，截面惯性矩I，接触线弛度f，材料轴向拉伸ΔL，质量m，刚度k，阻尼c，时间t，频率f，速度v，加速度g，垂向力F，张力T等物理量。

相应的质量缩比系数为Sm，几何尺寸缩比系数为SL，密度缩比系数为Sρ，加速度缩比系数为Sg。采用公式法计算单位长度重量。

基于式(4)可知，单位长度重量缩比系数的计算方法与式(3)单位长度重量的计算方法一致，是质量缩比系数与加速度缩比系数之积，除以几何尺寸缩比系数。其他物理量的推导方法相同，结果如表1。

表1 几何相似模型缩比系数表达式Table 1 Scaling factor expression of geometric similarity model

2) 缩比模型的验证

弓网耦合系统无论是在缩比模型还是原模型中，均在同一重力场下，故重力加速度的缩比系数Sg=1。结合实验场地的尺寸，确定其尺寸缩比系数为0.1；质量的缩比系数为Sm=0.01；密度缩比系数Sρ=1。弓网系统各物理量的缩比系数的计算结果如表2所示。

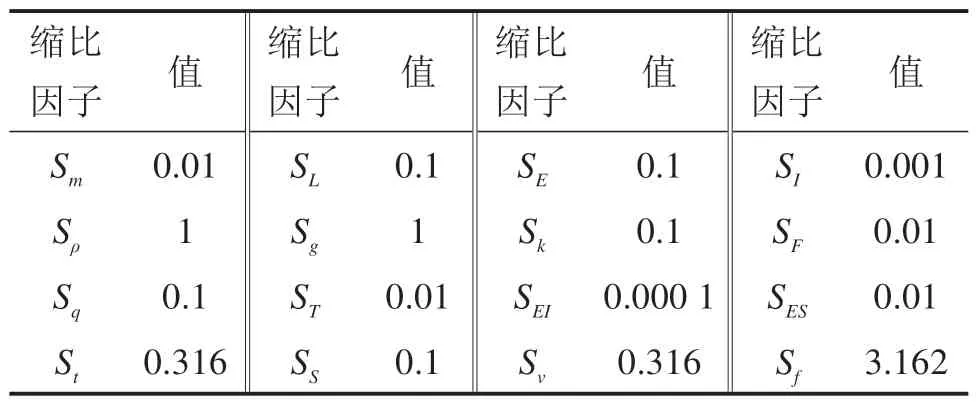
表2 几何相似缩比系数计算结果Table 2 Scaling factor calculation results of geometric similarity model

根据表2 中的缩比系数，在MSC.Marc 软件中搭建原模型和缩比模型，得到的计算结果如图2所示。其中图2(a)表示接触线高度，图2(b)表示受电弓高度，图2(c)表示弓网接触力。

图2 几何相似缩比模型仿真计算结果Fig.2 Simulation results of geometric similarity scaled model

从图2可知，原模型经缩比后，得到的缩比模型的接触线和受电弓的高度以及接触力的分布特征与原模型一致，相关系数为1，从而说明几何相似模型各物理量的缩比系数计算方法是合理的。

1.3 几何不相似模型相似关系的推导

从1.2 节表2 可知，在几何相似缩比模型中，接触网几何尺寸的缩比系数为0.1 时，速度缩比系数为0.316。即原模型运行速度是360 km/h 时，几何相似变换后的运行速度是100 km/h，进行实验研究仍具有较高难度。为了进一步降低实验室的运行速度本文基于几何不相似模型，进一步降低速度缩比系数，提出适合列车高速运行时实验平台的计算方法。

1) 缩比模型推导

保持几何尺寸缩比系数不变，即基于1.2 节的推导结果，将结合尺寸分为水平尺寸和垂向尺寸，分别用Lh和Lv表示。运行速度分为水平速度vh和垂向速度vv。其中，水平尺寸与垂向尺寸的关系可以表示为：

从式(5)和式(6)可知，保持水平尺寸缩比系数不变，增大垂向尺寸缩比系数，可以减小速度缩比系数，各物理量的缩比系数如表3所示。

表3 几何不相似模型缩比系数表达式Table 3 Scaling factor expression geometric dissimilarity model

2) 缩比模型的验证

对于几何不相似缩比模型，取质量缩比系数Sm=0.01，密度缩比系数Sρ=1，水平尺寸缩比系数SLh=0.1，垂向尺寸缩比系数Svv=0.25，经计算得到水平速度缩比系数Svh=0.2。得到弓网系统各物理量的缩比系数如表4所示。

表4 几何不相似模型缩比系数计算结果Table 4 Scaling factor calculation results of geometric dissimilarity model

根据表4 所示的缩比系数，在MSC.Marc 软件中搭建弓网原模型和缩比模型，得到计算结果如图3 所示。其中，图3(a)表示接触线高度，图3(b)表示受电弓高度，图3(c)表示弓网接触力。

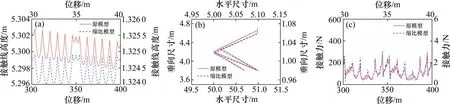
图3 几何不相似缩比模型仿真计算结果Fig.3 Simulation results of geometric dissimilarity scaled model

从图3可知，经过几何不相似变换后，虽然缩比模型的接触线高度与原模型存在差异，但是一个跨距周期内接触线高度的变化趋势一致，其Pearson 相关系数为0.919。从图3(c)可知，缩比变换前后的接触力的变化趋势基本一致，其Pearson相关系数为0.937。在通过静态和动态指标对比说明几何不相似变换计算缩比系数的方法是基本合理的。

2 弓网缩比模型的设计

2.1 缩比实验平台关键参数相似关系的选择

1.2 节和1.3节缩比系数的理论计算结果是搭建实验平台的基础。由于受实际的场地面积、材料类别等因素的限制，在进行实际材料选取时需要对关键物理量的参数选取进行综合考量。因此，需要进一步分析各参数对弓网接触力的影响程度，以便后续参数选取。

首先进一步改变吊弦的杨氏模量、线密度及接触线的抗拉强度、抗弯刚度等参数，分析接触力的变化规律，得出的接触压曲线如图4所示。

图4 接触网参数对接触力的影响Fig.4 Influence of catenary parameters on contact force

从图4 可知，列车以300 km 时速运行时，吊弦的线密度、接触线的抗弯强度对弓网接触力的影响较大，而吊弦的杨氏模量和接触线的抗拉强度对接触力的影响相对较小。因此，接触线的抗弯强度、吊弦的线密度需满足相似关系。

由于受电弓的弓头质量、弹簧刚度等参数对弓网接触力的影响程度较大[19]，因此，弓头质量、弹簧刚度等受电弓参量必须符合相似关系。基于1.2 节和1.3 节提出的几何相似和几何不相似2 种模型缩比系数计算方法，针对表5中原模型的接触网和受电弓参数、几何实际场地的尺寸及实际材料属性，几何相似模型的尺寸缩比系数定为0.1，几何不相似模型的水平尺寸缩比系数定为0.1，垂向尺寸缩比系数定为0.25。

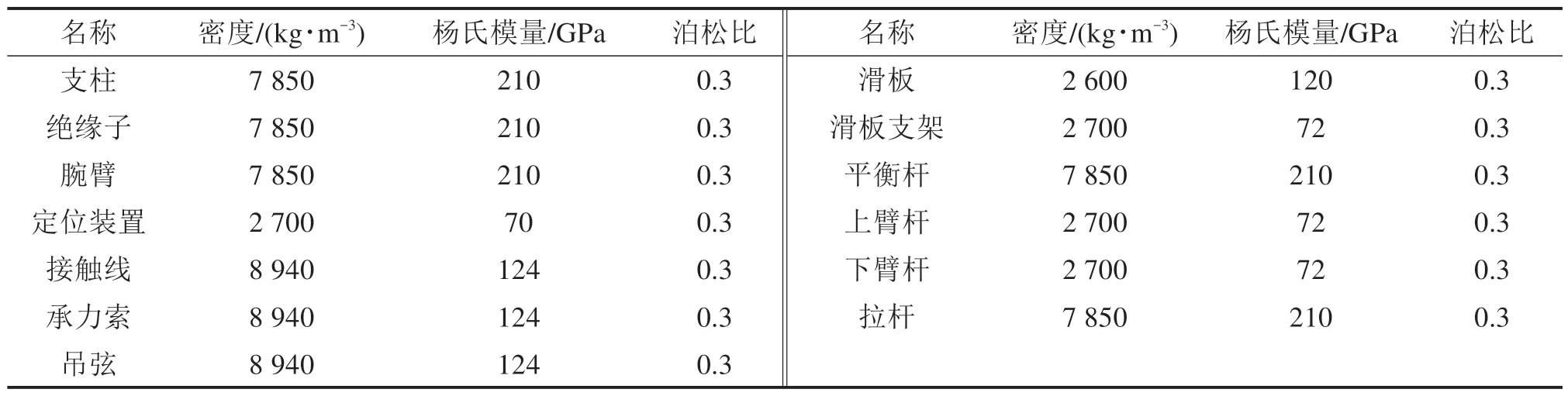
表5 原模型材料属性Table 5 Material properties of prototype

2.2 几何相似缩比模型的设计

基于1.2 节计算得到的缩比系数，缩比后的接触线和承力索的杨氏模量理论结果为12 GPa，密度为9 000 kg/m3，由于这种材料在实际生活中并不常见。综合考量材料的抗拉强度、截面应力及杨氏模量等参量，缩比模型选取铜作为接触线和承力索的材料。考虑到截面抗弯强度，接触线和承力索的截面设置为矩形。吊弦也采用铜材料，定位装置采用铝合金材料。受电弓各个部分材料与表5中受电弓原模型材料一致。弓网系统关键参量的材料选取结果如表6所示。

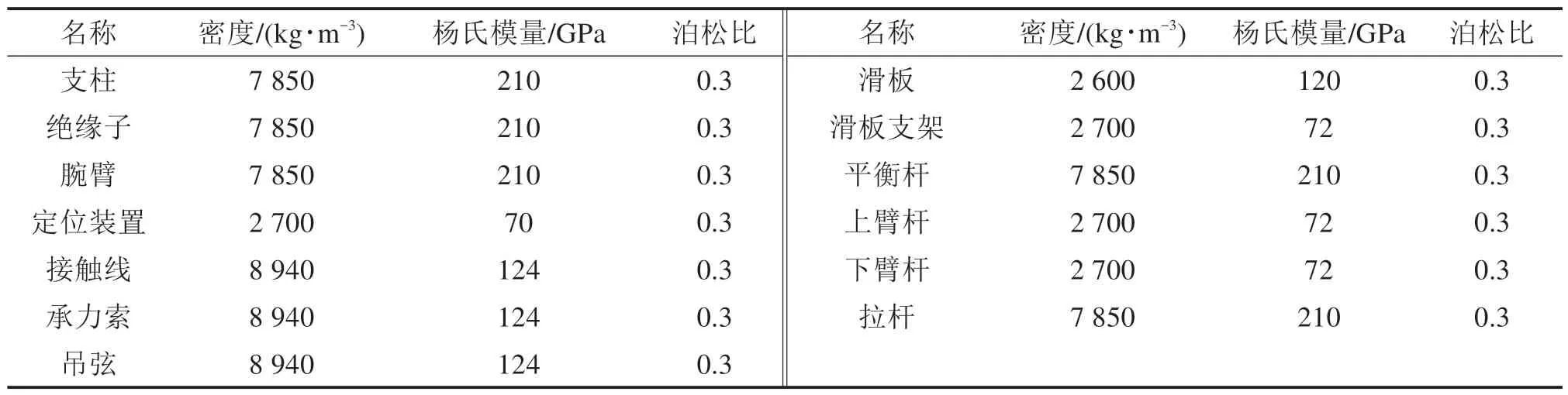
表6 几何相似缩比模型材料属性Table 6 Material properties of geometric similarity scaled model

根据表6 中弓网系统的材料选取结果，在MSC.Marc 软件中建立几何相似模型。缩比前，受电弓的运行速度为300 km/h；缩比后，受电弓的运行速度为95 km/h。计算得到的结果如图5所示。

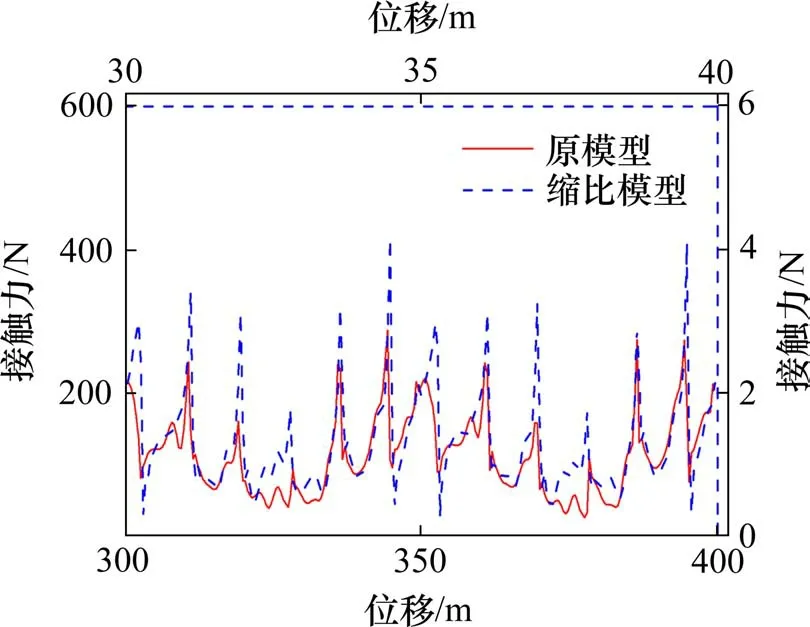
图5 几何相似缩比模型接触力Fig.5 Contact force of geometric similarity scaled model

从图5可知，各部分材料通过实际选材后，缩比模型接触力的变化趋势及局部极值点的出现位置与原模型基本一致，其Pearson相关系数为0.72。说明几何相似模型的设计过程是合理的。可以认为基于此缩比模型开展实验研究是基本合理的。

2.3 几何不相似缩比模型的设计

基于1.3 节几何不相似模型的缩比系数可知，接触线和承力索的SEI=0.000 04。为了保证SEI不变，通过减小杨氏模量E，增大截面惯性矩I来选择材料。因此，在本文中接触线、承力索、吊弦选用铅材料，杨氏模量减小为17 GPa。几何不相似模型的材料的选取结果如表7所示。其中，受电弓的参数与表6一致。

基于表7 的计算结果，在MSC.Marc 软件中搭建缩比模型。缩比前原模型的运行速度为300 km/h；缩比后的运行速度为60 km/h，得到图6 所示的弓网接触力曲线。

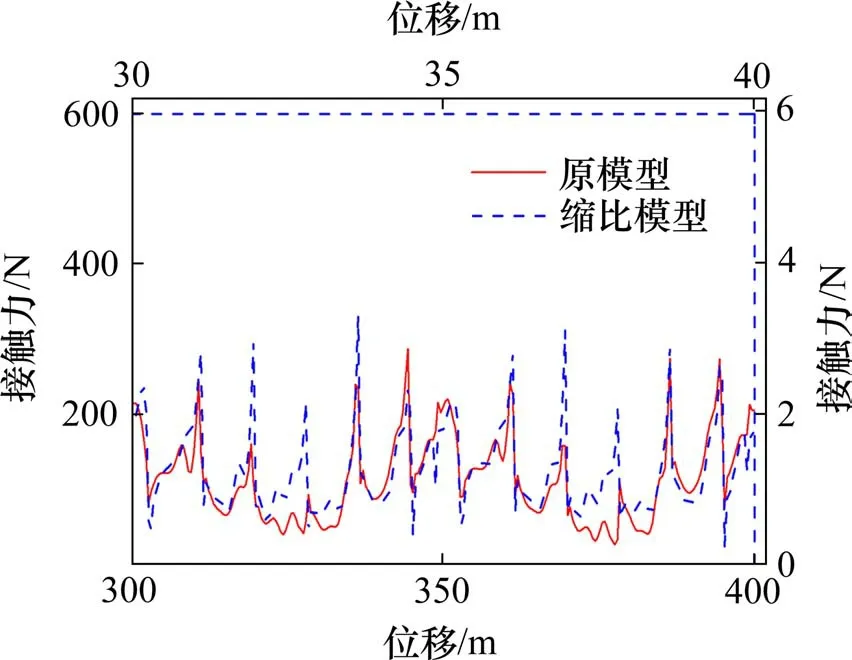
图6 几何不相似缩比模型接触力Fig.6 Contact force of geometric dissimilarity scaled model

在图6中，几何不相似模型的材料经过实际选材后，接触力变化趋势及峰值点的出现位置与原模型基本一致，相关系数为0.76。说明经过实际选材后的几何不相似模型的设计过程及结果是基本合理的，且该模型基本可以用于实验研究。

3 缩比模型静态和动态特性仿真计算分析

基于2.2 节和2.3 节缩比模型的设计结果，分别在静态和动态特性2个角度验证缩比模型的合理性。且在本节的对比分析中，均是将缩比模型的计算结果转换到相同尺度下与原模型进行对比分析的。

3.1 接触网刚度分布

列车运行过程中，接触网刚度分布是评价接触网静态特性的主要指标之一。在本文中根据EN50119 标准中规定的刚度计算方法[20]，计算接触网各位置点的刚度值。主要是通过在接触网各点施加1.4 N 的静态抬升力，得到各点的静态抬升量，进而计算接触网刚度，如图7所示。

图7 接触网刚度分布对比Fig.7 Comparison of catenary stiffness distribution

从图7中可知，经过相似变换后，缩比模型的刚度分布特征与原模型基本一致，其相关系数分别为0.997与0.998。缩比模型和原模型均在各吊弦悬挂点出现接触网刚度峰值。受接触网结构特征的影响，接触网刚度以吊弦间距和跨距为周期进行变化。且在定位点附近的刚度较大，跨距中部的刚度值较小。在图7中，缩比后的模型与原模型的刚度具有高度的一致性，但是在定位点两侧的首末吊弦点处也存在明显的误差。对于几何相似模型，首末吊弦点处的刚度与原模型的刚度误差值为1.3%；几何不相似模型的误差值是2.2%，均处于可接受的范围。

3.2 接触网及受电弓的固有频率

弓网接触力的变化与弓网间的耦合振动密切相关。且受电弓的弓头质量、弹簧阻尼等直接影响接触力的变化。尤其是与接触网耦合振动以后，受电弓处于受迫振动状态。受电弓的固有频率直接影响其受迫运行时与接触线间的接触状态，影响接触力的变化。因此，缩比模型受电弓和接触网的固有频率经缩比变换后也要与原模型基本一致。

经计算，受电弓缩比模型和原模型的前3阶固有频率如图8所示。

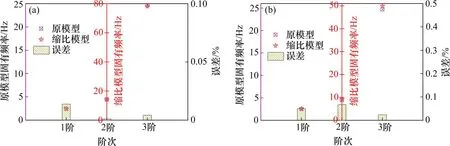
图8 受电弓固有频率Fig.8 Natural frequency of pantograph

从图8可知，几何相似和几何不相似模型的固有频率在相同尺度下均与原模型一致。但是，几何不相似模型的固有频率误差比几何相似模型略大，且最大误差为6.77%，仍处于可以接受的范围。

接触网原模型与缩比模型的前8阶固有频率如图9所示。

图9 接触网固有频率Fig.9 Natural frequency of catenary

对比图9(a)和9(b)可知，几何相似和不相似模型的前八阶固有频率转换到相同尺度下基本与原模型一致，但是几何相似模型的固有频率比几何不相似模型略小，且最大误差为5.4%，处于可以接受的范围。

3.3 接触力特性

受接触网结构特征的影响，接触网刚度在吊弦点及定位点出现刚度极大值点，在这些位置均会出现接触力峰值。且速度越高，这一现象越明显。但是，目前很少有关于吊弦点处接触力峰值的研究。本文采用文献[21]中的小波变换法，对接触力进行变换，提取吊弦点的吊弦间距幅值分量和跨距幅值分量，如图10 所示。其中，D1，D2，…，D6表示吊弦点。

图10 弓网接触力特性Fig.10 Contact force between pantograph and catenary characteristics

从图10(b)和10(c)可以看出，缩比模型的跨距与吊弦间距分量与原模型存在一定偏差，吊弦间距分量偏差大于跨距分量，2 种缩比模型最大偏差分别为160%，76.2%。这是因为经缩比变换以后，缩比模型各吊弦点的刚度略大于原模型。当受电弓运行到吊弦点处时，在接触网刚度的影响下，该处的接触力峰值明显增大，即吊弦间距幅值分量增大。随着运行速度的提高，吊弦间距幅值分量均呈增大趋势，跨距幅值分量呈先增大后减小的趋势，缩比模型与原模型的变化趋势基本一致，说明缩比模型可以用于高速铁路弓网动态研究。

3.4 弓网离线特性

随着列车运行速度的提高，受轮轨振动及气动激扰的影响，弓网振动加剧，严重时甚至会出现弓网离线。本文采用离线位置和离线时长作为衡量离线特性的评价指标[4]。改变原模型、几何相似及几何不相似模型的运行速度，分析离线特征参量的变化规律。其中，原模型的运行速度为400，425 及450 km/h。经过几何相似及不相似变换后的运行速度如图11所示。

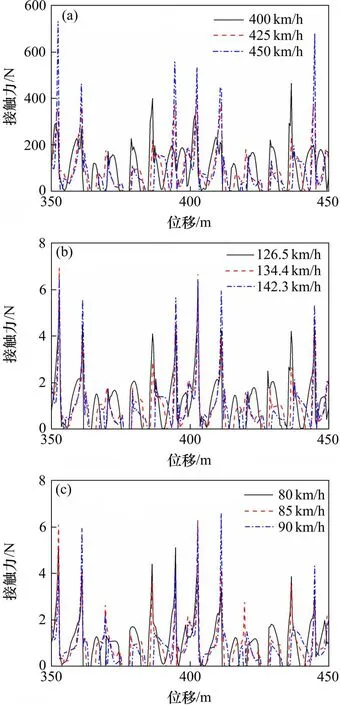
图11 离线位置Fig.11 Offline location

从图11 可知，随着受电弓速度的增大，原模型与缩比模型离线位置点均向受电弓的运行方向偏移。这是因为受电弓的运行速度越大，其运行状态越难改变，使离线点向受电弓的运行方向偏移。从图中还可以看出，随着运行速度的提高，离线点增多。这是因为运行速度提高，弓网间的振动加剧，原模型和缩比模型的离线点增多。从图11 中可以看出，在同一速度下，原模型与几何相似、几何不相似模型随跨距的变化，离线位置基本一致，说明缩比模型可以用于高速铁路弓网离线位置研究。

图12 是原模型和缩比模型不同位置离线点的离线间距。

图12 离线时长Fig.12 Offline duration

从图12 可以看出，在同一速度下，缩比前后的模型均是跨距中部离线点的持续时间大于定位点两次的首末吊弦点处，且离线时长随跨距周期的变化规律基本一致。随着速度的变化，原模型和缩比模型的变化规律基本一致。也就是说，几何相似和几何不相似缩比模型可以用于高速铁路弓网离线时长研究。

综上所述，原模型和缩比模型的接触网刚度分布、固有频率、接触力、离线特征的变化规律均基本一致。从静态和动态2个角度说明缩比模型可以用于高速铁路弓网关系研究。

4 结论

1) 根据相似理论提出了2种缩比模型，推导出了2种模型缩比系数的计算方法；然后结合实际材料属性提出了模型的具体选材方法。

2) 从静态角度验证了2 种缩比模型的合理性。原模型和缩比模型的接触网刚度分布、固有频率的数值基本一致，误差处于可接受范围，从静态角度说明2种缩比模型可以用于高速铁路弓网关系研究。

3) 从动态角度验证了2 种缩比模型的合理性。随着运行速度提高，原模型和缩比模型的接触力及离线特性的变化趋势基本一致，从动态角度说明2种缩比模型可以用于高速铁路弓网关系研究。

基于本文提出的缩比模型得出的接触压力、刚度分布、离线特征等与原模型得出的结果的变化规律虽然基本一致，但在进行缩比实验平台搭建时，实际场地及施工情况均可能会增大缩比平台误差。因此，在缩比实验平台搭建完成后，还需进一步进行误差测算。研究团队后续拟基于缩比实验平台进行原比例实验平台上难以进行的时速400 km及以上的弓网关系及离线电弧研究。