矩形前缘剪切流对圆柱气动和绕流特性影响规律的研究

李文舒，王汉封, ，李欢, ，何旭辉,

(1.中南大学 土木工程学院，湖南 长沙 410075；2.中南大学 高速铁路建造技术国家工程研究中心，湖南 长沙 410075)

桥梁电缆、电力线路、冷却塔、高层建筑及海底管道等多种圆柱形结构在土木工程、机械工程和海洋工程中得到了广泛应用。圆柱形结构周围的流场包含剪切层、尾涡和卡门涡街[1-2]之间的相互作用，这些相互作用在圆柱体周围产生了各种流动模式。在过去的几十年里，对双圆柱绕流[3-6]的气动特性和流动特性已经有了相当深入的研究，与串列和并列相比，交错排列的双圆柱在现实生活中的应用更为广泛。在不同的中心间距比P/D(P为圆柱圆心之间的距离，D为圆柱直径)和入射角β(来流与圆心连线的夹角)条件下，上游圆柱的剪切层打在下游圆柱的不同位置上，对下游圆柱的气动力和流场形态[7-9]产生明显的影响。PRICE 等[10]研究了在雷诺数Re=3.2×104～7.4×104，P/D=1.125～4.0，β=0°～90°的条件下，2 个直径相等的交错圆柱体的平均空气动力系数和涡脱频率。文章根据中心间距比对双圆柱流型进行分类。当P/D=1.125～1.25 时，属于紧密间距，其双圆柱的流型类似于单个钝体；当P/D=1.5～2.5时，属于中等间距，当入射角较小时会产生负升力以及相应的负阻力和较高的St数(涡脱频率)；当P/D=3～4时，属于大间距，2 个圆柱的流场互不干扰，气动特性类似于孤立圆柱。WU 等[11]采用大涡模拟的方法，研究了高亚临界雷诺数(Re=1.4×105)条件下，2个交错圆柱在P/D=1.5～4，β=0°～90°条件下的绕流问题。研究发现，当P/D=1.5～2，β=0°～10°时，高速间隙流的出现导致下游圆柱迎风侧局部区域产生强大的负压，从而产生负阻力；当P/D=1.5～3，β=10°时，下游圆柱会产生负升力；当P/D=3～4，β=20°时，下游圆柱产生正升力。GU等[12]研究了在高亚临界雷诺数条件(Re=2.2×105)下，2 个相同圆柱交错排列时的压力分布干扰。根据不同的压力分布模式，按照入射角β将下游圆柱的流型分为尾迹型、剪切层型和领域干涉型。在β=9°～20°时，会产生剪切层流型，此时下游圆柱的间隙面出现较大负压区，这是由于上游圆柱间隙侧分离的剪切层高速侧重新附着在下游圆柱间隙侧，以及下游圆柱间隙侧高频率有规则的旋涡脱落。由于圆柱气动特性和流动特性易受雷诺数的影响，已有研究选取的雷诺数大小不一，故很难得出一致的结论。相比圆柱，矩形板的剪切层较为稳定，基本不受雷诺数影响，因此如果将上游圆柱换成无限长的矩形板，可以使下游圆柱受到稳定的流动干扰，有利于对其进行气动特性分析。此外，高速列车、桥梁缆索和风屏障檩条等结构常常浸没在桥梁前缘剪切流中，矩形板和圆柱组成的异构抽象模型类似于实际工程中的车桥模型，探究矩形前缘剪切流对下游圆柱的影响对研究桥上行车安全性和稳定性有一定的参考价值。鉴于此，本文通过测压试验，研究圆柱的气动特性与圆柱和矩形前缘相对位置以及雷诺数之间的关系，进一步揭示和探讨矩形前缘剪切流引发的圆柱绕流的雷诺数效应。

1 风洞试验介绍

试验在中南大学风洞实验室CSU-3 风洞进行，该风洞为闭口环流式，试验段尺寸为800 mm×120 mm，风速控制范围为0～25 m/s，湍流度小于0.5%。

本试验为刚性模型测压试验。模型如图1 所示。圆柱直径为D=60 mm，矩形板厚度为H=48 mm。测压试验中，圆柱压力测点沿模型跨中位置周向布置，1 号测点正对来流。在圆柱发生流动分离附近(8～13 号测点、27～32 号测点)每8°设置一个测点，其余位置每隔10°设置一个测点。圆柱模型材质为铝合金，矩形板模型材质为ABS 板。试验模型安装如图2所示。

图1 模型尺寸及测点布置Fig.1 Model size and measurement point arrangement

图2 试验照片Fig.2 Test photo

试验探究3 组参数G/D，L/D和Re对圆柱气动特性的影响。其中，圆柱直径D=60 mm，G为圆柱下表面距矩形板上表面的垂直流向距离，L为矩形板前缘距圆柱圆心的水平流向距离。具体含义如图1所示。具体试验工况如表1所示。

实验中自由来流风速U∞为10～25 m/s，对应Re为4×104～1×105。模型表面的压力测压点平均风压系数Cp与脉动风压系数C′p的定义如下[13-14]：

式中：P为各测点风压的平均值；P∞为风洞静压；Prms为脉动风压的均方根值。由此亦可通过面积积分的形式计算模型总体的平均阻力系数Cd，平均升力系数Cl，脉动阻力系数和脉动升力系数。

2 结果与讨论

2.1 气动力系数

2.1.1 不同G/D和不同L/D条件下圆柱气动力的变化

图3所示为圆柱和矩形板的相对位置对圆柱气动力特性的影响规律，图中的圆点为试验工况的位置。Cd的分布规律与矩形前缘形成的剪切层的形状相似。越靠近矩形板的上壁面，圆柱的Cd越小，即Cd随着G/D的减小而减小，这一现象与近壁面圆柱绕流中圆柱的阻力特性类似。当G/D较小时，Cd较小而Cl较大，且Cl随着G/D的增大而减小，当G/D增大到一定值时，圆柱会产生负升力。总体变化不大，圆柱越靠近矩形前缘，其越小。圆柱的C′l的变化规律与近壁面圆柱的类似，即C′l随着G/D的减小而减小，这一现象也与参考文献[15-17]中G/D较小时圆柱的涡脱会受到抑制这一结论吻合。

图3 气动力系数随圆柱和矩形板相对位置的变化Fig.3 Aerodynamic coefficient varies with the relative position of the cylinder and rectangular plates

2.1.2Re对圆柱气动力的影响

图4 所示为当G/D=0.1 时，雷诺数对圆柱气动力的影响。很明显，在本文研究的雷诺数范围内，当圆柱距离矩形板前缘很近(L/D=0.60)时，圆柱气动力的雷诺数效应不明显。由于近壁面的影响，圆柱在距离矩形前缘不同位置处的阻力系数都低于孤立圆柱的阻力系数(Cd=1.2)，当L/D≤2.02时，Re对Cd的影响很小，当L/D≥3.00 时，Cd随着Re的增大而减小。当L/D=1.60 和L/D=2.02 时，升力系数的绝对值随着Re的增大而增大，随着L/D的增大，Cl随着Re的增大而增大，并且会逐渐由负值恢复为正值，且Re越大，零升力对应的L/D越小。

如图5所示，在氧化阶段，随着入炉物料的不断增加，金属和炉渣量不断增多，熔池高度持续上涨，这时应及时将产出的金属铅和铅冰铜排出，一方面生成的金属铅不被重新氧化进入炉渣，使渣含铅升高，一方面熔池高度得以控制，让氧化阶段更加持久；在还原阶段，随着炉渣中的铅不断被还原成粗铅及时排放，炉渣量和熔池高度不断降低，当炉渣含铅量和熔池高度降至工艺目标值时，便可转入烟化阶段进行铅锌的烟化挥发；在烟化阶段，粗铅已排放干净，熔池高度在900～1200 mm之间，根据熔炼顶吹炉的工业生产时间可知，这一范围的熔池高度对贫铅渣的烟化非常有利，可将炉渣含铅量降低至目标值。

图4 当G/D=0.1时，雷诺数对圆柱气动力的影响Fig.4 Effect of Reynolds numbers on cylinder aerodynamics when G/D=0.1

2.2 平均风压系数

2.2.1G/D对Cp的影响

图5 以L/D=1.60 和L/D=4.40 为例，表明了在Re=1×105的工况下，圆柱的平均风压系数随G/D的变化情况。随着G/D的增大，圆柱产生的较大负压区由上侧逐渐转移至下侧，最后平均风压实现基本对称分布，这与参考文献[18-19]中近壁面圆柱绕流的规律相似。因此可以认为，圆柱发生湍流转捩的位置与矩形前缘剪切流打在圆柱上的位置有关。在L/D相同的条件下，圆柱的风压驻点随着G/D的减小而向下游移动，背压随着G/D的增大而增大。相较于圆柱下部的分离点区域，圆柱上部分离点区域的平均风压受G/D的影响较小，且随着G/D的增大，圆柱上部的负压极值点逐渐向上游移动。从图5的变化可以看出，在G/D较大的情况下，当L/D较小时，圆柱平均风压基本上呈对称分布，而随着L/D的增大，其对称性逐渐减弱，因此，下一步探究L/D对圆柱流动的影响。

图5 平均风压系数随G/D的变化Fig.5 G/D dependence of Cp-mean

2.2.2L/D对Cp的影响

图6 以G/D=0 和G/D=0.2 为例，表明了在Re=1×105的工况下，圆柱的平均风压系数随L/D的变化情况。当G/D=0 时，在圆柱与矩形板上表面接触的位置(θ=270°)，平均风压的突变程度在L/D=0.60 时最大，之后随着L/D的增大，突变程度先增大后减小。随着L/D的增大，风压驻点从圆柱下侧偏移至圆柱上侧，且驻点处的风压值逐渐减小，并伴随有圆柱上部流动分离点逐渐向下游移动的现象。由图5 和图6 可知，圆柱在相对矩形板前缘不同位置产生不同气动特性的机理与剪切流打在圆柱上的位置有关。

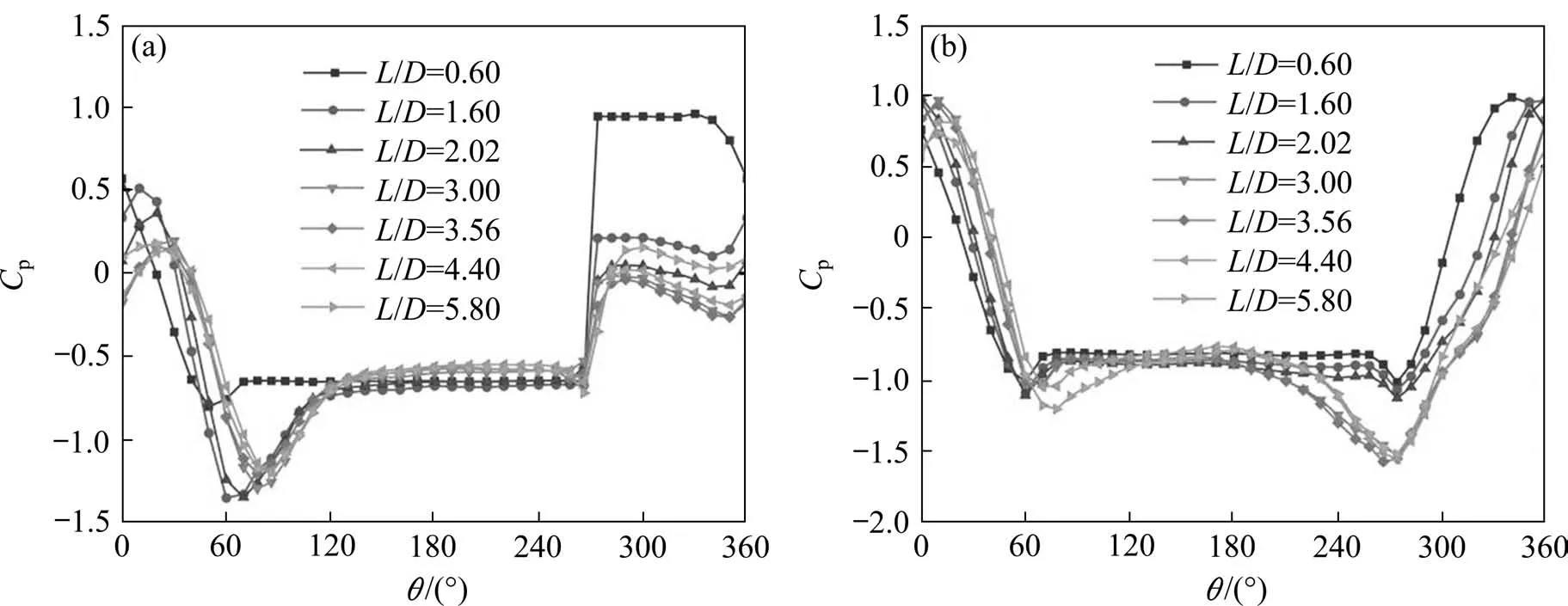
图6 平均风压系数随L/D的变化Fig.6 L/D dependence of Cp-mean

2.2.3Re对Cp的影响

图7 以L/D=0.60 和L/D=3.56 为例，表明了当G/D=0.1 时，圆柱平均风压随Re的变化情况。可以看出，在本文研究的雷诺数范围内，当圆柱距离矩形板前缘很近(L/D=0.60)时，圆柱风压的雷诺数效应不明显。随着L/D的增大，雷诺数主要影响圆柱的背压以及流动分离区的负压，随着Re增大，负压极值点向下游移动，负压极值增大，背压减小，从而导致分离泡的体积随着Re增大而增大。有趣的是，在圆柱与矩形前缘特殊的相对位置处会出现雷诺数影响圆柱湍流转变的情况，即当G/D=0.10 和L/D=3.00，G/D=0.10 和L/D=3.56，G/D=0.10 和L/D=4.40 时，Re会影响湍流转变的位置，在这些工况下，随着雷诺数的增大，圆柱发生湍流转变的位置会由下侧转移至上侧，且不会出现由上侧转移至下侧的相反情况。

图7 平均风压系数随Re的变化Fig.7 Reynolds number dependence of Cp-mean

2.3 涡脱频率

图8 圆柱涡脱频率随L/D和G/D的变化规律Fig.8 Regularity of cylindrical vortex frequency with L/D and G/D

2.4 瞬时风压

2.4.1 圆柱瞬时风压的双稳态现象

图9 所示为圆柱双稳态现象随L/D的变化规律，其中横坐标表示对时间的无量化，纵坐标为圆柱平均风压系数。双稳态现象只在G/D=0.4时发生，且随着L/D的增大，双稳态现象逐渐减弱。ALAM等[13]曾在交错双圆柱绕流试验中观察到，当P/D=1.1～2.3，β=10°(β为双圆柱圆心连线和来流方向的夹角)时，下游圆柱会出现双稳态现象，并指出该现象与下游圆柱间隙侧表面分离泡的形成和破裂有关。对于本文出现的双稳态现象的机理将在后续的试验中进一步研究。

图9 圆柱发生双稳态现象对应的风压时程Fig.9 Wind pressure time range corresponding to the phenomenon of bistable state occurring in the cylinder

2.4.2 圆柱瞬时风压的转捩现象

图10 所示为在L/D=4.40，G/D=0.20 的工况下，圆柱的瞬时风压随雷诺数的变化，左侧是风压时程图，右侧是对应的概率密度函数图。其中，实线代表高斯分布，虚线代表测点风压的概率密度分布，分别取各工况下平均风压负压极值和脉动风压最大的点进行分析，纵坐标与左侧图相对应，表示测点的瞬时风压，曲线与纵坐标围成的面积为1。通过分析，这些工况下发生转捩的位置都在9 号测点附近(如图1 所示)。在图10(c)中(Re=8×104)，右侧对应的概率密度函数出现了双峰特征，表明圆柱出现在临界雷诺数区才会出现的时程转捩现象[20-21]。若降低或增大来流雷诺数，如图10(a)，10(c)和10(d)，双峰现象会消失，非高斯分布特性也逐渐减弱，因此圆柱的转捩现象只在特定雷诺数且只在其相对于矩形板的特定位置时才会发生。由图10 可知，随着雷诺数的增大，圆柱经历了由转捩开始到正在转捩再到转捩完成的一个过程。除了图10 所提到的L/D=4.40，G/D=0.20这一工况，在L/D=3.00，G/D=0.10；L/D=3.56，G/D=0.20；L/D=5.80，G/D=0.30 时，同样会出现类似图10(c)的现象。可以看出，这些发生转捩现象的工况，其圆柱与矩形板相对位置的变化特点是L/D随着G/D的增大而增大，这与矩形板前缘产生的剪切流发展的形式类似。因此，从风压时程分布曲线可以进一步确定，由于矩形板前缘产生的剪切流在圆柱流动分离的位置产生了局部流动加速，从而使圆柱局部雷诺数增大，使得圆柱在亚临界雷诺数区间呈现出临界雷诺数区间的流动特性。在杜晓庆等[22]的双圆柱绕流相关文献中提到，在特定的双圆柱相对位置的情况下，由于上游圆柱形成的加速剪切层打在下游圆柱上，导致下游圆柱的局部位置产生较大负压，阻力系数突降。类比得到，矩形板与圆柱在特定的相对位置也会由于矩形板前缘剪切层加速，从而使圆柱在亚临界雷诺数区间产生临界雷诺数区间才会有的气动现象。

图10 当L/D=4.40,G/D=0.20时，圆柱的风压时程和概率密度函数随雷诺数的变化Fig.10 Wind pressure time history and probability density function of a cylinder change with Reynolds number when L/D=4.40,G/D=0.20

3 结论

1) 圆柱在相对矩形板前缘不同位置时，会产生不同气动特性的机理，这与剪切流打在圆柱上的位置有关，圆柱相对矩形板处于不同位置时，会产生不同的风压分布、气动力分布以及涡脱特性。

2) 圆柱与矩形板处于特定的相对位置时，矩形前缘剪切流的加速侧打在圆柱上，会使圆柱局部雷诺数增大，从而在亚临界区产生临界区的气动特性，且该相对位置的特点是G/D随着L/D的增大而增大。

3) 当G/D=0.4时，圆柱会产生双稳态现象，且随着L/D的增大，双稳态现象逐渐减弱。