离网格压缩匹配场处理

兰旭辉 杨成竹 徐立军

（北京理工大学信息与电子学院，北京 100081）

1 引言

海洋覆盖了地球约三分之二的面积，具有丰富的资源和广阔的发展前景，对于人类的生存和发展具有重要意义。海洋中蕴含着各种有用的资源，如石油、天然气、矿产、海洋能源等。科技的进步带来了对海洋资源日益增长的需求，世界各国争先投入大量精力对海洋进行探索和开发。许多关键任务都需要在水下环境中进行，例如资源勘探、水下运输与安装、海洋科学研究等。在这些任务中，水声被动定位作为一项关键技术引起了广泛的关注［1-5］，被动定位具有高安全性、高隐蔽性等优点，它是指根据水听器接收到的来自目标区域内声源信号的声压数据，通过适当的信号处理算法，在搜索范围内寻找最佳或最有可能的声源位置。在水声被动定位中，主要考虑通过接收声压来定位水下目标的位置，但声信号的传播会受到水下环境的复杂影响，例如海洋温度、水深、水质、潮汐变化、海底参数等因素，这些因素可能会引起信号的衰减、畸变和多径效应带来的影响，因此如何获取准确的海洋参数并进行水下目标定位成为了一个极具挑战性的问题［6-7］。

在过去的几十年里，已经提出了许多水声被动定位的方法。其中一些研究是基于经典的匹配场处理（Matched Field Processing，MFP）算法，该方法最早是由Bucker 等人提出，是一种典型的线性匹配场处理器。该方法通过场景的需求选取合适的声场模型预先计算出拷贝场向量，将基阵接收到的复声压与已知的复制向量字典相关联匹配来确定声源的位置，常用于远程被动定位。近年来，匹配场处理在海洋环境参数已知的场景下得到广泛应用［8-9］，各类改进的匹配场处理算法［10-11］也被陆续提出，以适应复杂环境获得更好的定位性能。然而由于MFP在拷贝场的计算中考虑了声传播模型多径效应的影响，其对准确环境参数的依赖性较高，当环境失配时会导致定位结果不理想；与之同时，传统MFP由于其具有宽主瓣和高旁瓣而导致分辨率较低［12］，且MFP 方法只能在预设的距离-深度网格点上进行源定位，当声源偏离网格点时，存在固有的定位性能极限；此外，由于网格失配带来的影响将会导致定位性能下降，这使得该方法的定位精度存在一定的局限性。

近年来，随着稀疏表示和压缩感知等新兴技术的出现，基于目标空间稀疏性的水声被动定位方法也逐渐受到了研究人员的关注，提出了压缩匹配场处理（Compressive Matched Field Processing，CMFP）用于被动声源定位［13-14］。该方法需要信号具有稀疏性，将MFP 中划分为网格的拷贝场作为传感矩阵，使用优化算法对信号进行稀疏重构来确定声源的位置。由于声源的数量远小于候选网格点位置的数量，水声信号在空间域中本质上是稀疏的，可以将源定位重新表述为稀疏信号恢复问题。基于贪婪类的算法如正交匹配追踪或基于凸优化的基追踪等算法可用于求解该问题，以估计不同候选位置的源功率［15］。压缩感知具有类似于自适应处理器的特性，即使在单源场景下也有望提供适度的性能提升。在对多个源进行定位时，CMFP 对比MFP 表现出更好的定位精度。然而CMFP也仅能将声源定位在网格点上，其性能受到网格失配的影响比较严重。对于离网格源，CMFP 可能会在定位结果附近呈现出一些模糊的峰，即出现多个稀疏解对应于一个单一源的情况。在现实场景中，即使联合处理多个频率和多个快拍进行定位也可能遇到该问题，导致定位不准确甚至是错误的定位结果。

在真实的处理场景下，源在目标区域中的位置是连续且任意的，声源不会落在网格点上，稀疏表示框架会面临网格失配的问题。网格失配在一定程度上可以通过部分网格细化来处理［16］，但当网格过于密集时，它也会呈现严重的模糊性。在波达方向角（Direction of Arrival，DOA）估计中引入了通过一阶泰勒级数展开近似的方法来估计离网格源［17-18］，该方法在实际应用中取得了显著的效果。然而对于水下声源定位问题，对声波在水下传播的波动方程进行求导的计算复杂度较高，难以通过类似的方法对源定位问题进行求解。

在本文中，提出了一种离网格压缩匹配场处理（Off-grid Compressive Matched Field Processing，OGCMFP）方法来解决离网格水下源定位问题。考虑到相邻水下位置之间的信道冲激响应（Channel Impulse Response，CIR）有较大的相似性，可以通过对真实源位置周围网格点处的复制向量进行线性插值来近似源位置处的信道向量。基于这一规律建立了一种群稀疏信号模型，并提出了相应的OGCMFP 算法来解决源定位问题，该算法可以高精度地估计声源具体的距离和深度，消除CMFP 在真实位置附近的多峰值模糊问题，实验结果证明了该方法的有效性和优越性。

2 预备知识

本节给出了MFP和CMFP的接收信号模型，并描述了相应的定位算法。在本文框架中，由N个水听器构成的垂直阵列接收到的频率为f的信号可以表述为

传统的MFP 将测量数据y与l2范数归一化后的复制向量进行关联匹配：

式中B(θ)表示位置θ处的匹配能量，R为样本协方差矩阵（SCM）

匹配出的峰值处则表示声源的估计位置。

现在，如果目标区域被预先划分为网格，当网格足够密时可以认为信号是在网格点处生成的［19-20］，由于声源数远小于候选网格点数，信号可以用稀疏框架表示。对于多快拍场景，接收到的阵列信号被重新表述为

式中A(f)=[a(f，θ1)，a(f，θ2)，…，a(f，θM)]∈CN×M表示包含所有M个候选位置复制向量的字典矩阵［21］。S(f)∈CM×L是所有候选位置的复振幅，N(f)是包含L个快拍的复高斯噪声。

对于处于单一频率f下的CMFP，定位估计表示为以下问题，通常称为群最小绝对收缩和选择算子［22］（Group Least Absolute Shrinkage and Selection Operator，group-LASSO）：

式中‖S‖2，1=∑n‖Sn‖2，Sn代表S的第n行［23］。λ＞0是与噪声相关的正则化参数，需要在处理时自行设定来控制解的稀疏性。

3 离网格压缩匹配场处理

在真实的场景下，声源位于网格点上的概率为p=0，将会引起网格失配。在本节中，提出了一种离网格压缩匹配场处理方法来解决此问题。

3.1 基于邻近格点线性拟合的离网格信号模型

本小节基于邻近格点线性拟合建立了离网格信号模型，对于水下声源定位，在模型中将目标区域划分为r个距离和d个深度，则离散化网格单元的总数为Q=(d-1)×(r-1)。假设第k个源位于第q个离散化网格单元中，则源位置的CIRbk∈CN由来自周围4个网格点处复制向量的线性组合近似。

式中βq，i为第k个源周围4 格点处复制向量的权系数，接收到的阵列信号重写为

式中sk是第k个源的多快拍信号。

现在将复制向量字典A=[a(θ1)，a(θ2)，…，a(θM)]划分出4 个子块A1，A2，A3，A4并重新排列，新的字典记为

式中A1∈CN×Q是由全部Q个网格单元左上角格点处对应的归一化复制向量组成的子字典。以相同的方式，A2，A3，A4是所有网格单元的右上角、左下角和右下角处复制向量组成的字典。注意到4个子字典中有很大一部分是重复的。例如在第q个网格单元中aq，2∈A2，同样的复制向量在第q+1个网格单元中被记为aq+1，1∈A1（如图1所示）。

图1 复制向量字典重排示意图Fig.1 A schematic diagram of the replica vectors dictionary rearrangement

图中aq，i表示第q个网格单元的4个复制向量，黄框内的格点代表A1中包含的全部复制向量，蓝框内的格点则代表了A4中的复制向量（这里未标注出A2，A3）。

通过上述字典重排后，信号模型重写为

Bi=diag(β1，i，β2，i，…，βQ，i)是Ai的系数矩阵。假设声源位于不同的网格单元内，SK∈CQ×L仅包含由K个源的复振幅构成的K个非零行。

3.2 基于群稀疏优化的离网格压缩匹配场处理

本节介绍了离网格压缩匹配场处理的信号恢复算法，使用群稀疏恢复的方法来估计，问题的基追踪去噪形式写为

式中η是误差容限，根据噪声水平和模型匹配程度来选择［24］。的第q项是第q个网格单元对应4 格点处信号组成的矩阵的F范数值，所以

这里可以将目标函数分为两个部分：

式中ht-1是上一轮迭代结果的梯度，μ是迭代的步长，令μ=1/2ζ，ζ为的最大特征值，则

考虑总体目标函数在对误差项进行半步更新的基础上，同时需要满足稀疏性约束。因此可以利用近端算子的方法，在当前变量附近找到一个群稀疏的解，使用以下迭代策略求解，即对于第t次迭代

其中ρ=λ/2ζ。

将式（20）按稀疏群展开为

将Q项逐一进行更新迭代至信号收敛或达到最大迭代次数。

在K源场景下，从恢复的信号中选择信号功率最高的前K个网格单元。声源的位置可以通过OGCMFP估计为

式中Si，k是Si的第k行，θk，i是第k个网格单元4 个格点处的距离和深度，归一化系数αk，i是βk，i/∑iβk，i的估计值。

3.3 基于SVD数据压缩的算法加速

当数据快拍数L较大时，会显著增加计算量，为了提高信号重构过程的运行速度，l1-SVD［26］提供了一种对数据降维的方法，并减少了信号重构对噪声的敏感性。由于信号是由K个源产生的，受传统子空间方法的启发，可以将多快拍数据Y∈CN×L（L＞K）分解为信号子空间和噪声子空间。通过奇异值分解（Singular Value Decomposition，SVD）保留属于信号子空间的部分YSV。

式中DK=[IK，0]，IK是K阶的单位矩阵。同时，对信号和噪声也进行降维，可以得到一个新的数据模型：

则优化问题的目标函数可重写为

将降维后的数据代替原式进行定位问题求解，使用l1-SVD后计算速度能得到极大的提升。

4 仿真实验

在本节中，对传统的MFP、CMFP 和本文提出的OG-CMFP方法进行了仿真实验，并验证了所提出方法的优越性能。

4.1 环境模型和数据生成

实验的海洋环境场景由典型的浅水波导模拟生成，环境参数从海试实验中获得。设置海水深度为216 m，海底由沉积层、泥岩层和半空间底部组成。海洋每层的声速剖面（Sound Speed Profile，SSP）、海底参数中密度、声速和衰减系数等如图2所示。接收阵列是由22个水听器组成的垂直线阵，信号的频率设置为133 Hz，阵元间距为5.6 m（半波长），最底端水听器部署在深度212 m处。

图2 实验的声速剖面和海底参数Fig.2 SSP and bottom parameters for experiments

实验在双目标源的场景下进行，两个声源的功率相同。源Ⅰ的位置在目标区域中随机生成。源Ⅱ在源Ⅰ附近，为了便于统计，源Ⅱ的设置位置比源Ⅰ更远、更深，且两源距离差在500～1500 m、深度差在0～20 m 范围内随机选取。复制向量由KRAKEN 计算得到。为了保证两源信号不相干，源信号各个快拍的相位从[0，2π)的均匀分布中选择。阵列信噪比（Signal to Noise Ratio，SNR）定义为单声源功率与噪声功率的比值。

对应于单次快拍的SNR，并假设加性高斯噪声在不同传感器和快拍之间独立同分布。

为了比较不同方法的性能，定位结果的准确率（Accuracy，ACC）和距离平均绝对误差（range mean absolute error，rMAE）分别定义为

式中C=500 是在每个SNR 下的蒙特卡罗实验次数。是声源的距离和深度估计结果，ri和di表示真实的距离、深度位置。

4.2 仿真结果

现将本文提出的OG-CMFP 与MFP 和CMFP 的定位性能进行对比，所有模糊平面都进行了峰值归一化处理以便在绘图时直观比较。实验中声源位于1～10 km 的范围内，深度为10～200 m。目标区域被划分为距离间隔为0.05 km、深度间隔为10 m 的离散网格，信号快拍数L=30，模糊平面如图3所示。在单次随机实验中，SNR=0 dB。两个离网格源分别位于（4.973 km，82.70 m）和（6.324 km，96.87 m）的距离和深度位置。从图3（a）中可以看出，传统MFP 呈现出严重的模糊性，且干扰峰较多。CMFP可以在真实位置附近找到一些可能的峰值位置，但仍存在不确定性，其性能容易受到网格失配的影响。OGCMFP则呈现出最佳的性能，消除了离网格情况导致的峰值模糊，基于四周网格点的联合恢复使该算法能够从相邻的复制向量中学习到更准确的信道信息，从而提高定位的准确性。对于源Ⅱ，定位结果中得到了0.002 km 的距离估计误差和1.49 m 的深度估计误差，这优于传统MFP和CMFP的性能极限。

图3 双源定位的模糊平面（SNR=0 dB）Fig.3 Ambiguity surfaces for two-source localization （SNR=0 dB）

为了与声源在网格节点上的情景进行直观的对比，在SNR=0 dB 的条件下，两个在格点上的源的距离、深度信息分别设置为（5.000 km，80.00 m）和（6.300 km，100.00 m），三种算法的模糊平面如图3（b）所示。可以观察到即使声源处于格点上，MFP在多源定位时仍存在许多干扰峰且峰值较高，容易发生错判得到较差的定位结果。CMFP 在源处于格点时能够实现较好的定位结果，对比离网格场景干扰峰更少，此时在真实位置附近没有呈现出多峰值带来的定位模糊，但处于网格点上的条件在现实中难以实现，离网格场景更具有普适性。OG-CMFP则在此次双源定位实验中存在0.023 km 的平均距离误差和2.97 m 的平均深度误差，尽管在处理位于格点上的声源时，该算法会因为多个网格交汇的影响导致定位精度有所下降，但引起的误差是可以接受的，定位结果仍然准确，因此OG-CMFP具有较好的鲁棒性，能适用于各种场景获得更好的定位精度。

本文实验所用计算机CPU 型号为Intel Core i9-11900 K，时钟频率3.50 GHz，使用的软件为MATLAB R2020b。表1 展示了不同算法的运行时间，可以看到传统MFP 方法计算速度最快，但其定位质量较差；所提出的OG-CMFP 方法由于将原字典矩阵进行分块重组，使得字典的维数增加了近4倍，从计算时间上来看，与CMFP 进行对比，OG-CMFP 的运行时间也上升到CMFP 的约4 倍，其计算成本与字典维数近似呈线性关系。

表1 各定位算法的运行时间Tab.1 Running time of different algorithms

图4展示了在不同SNR下的定位准确率，声源在目标区域内呈均匀分布。在网格单元中提取恢复信号的功率里最大的两个峰值，认为近处的峰对应于源Ⅰ的位置而较远峰则对应源Ⅱ，将两声源的平均定位准确率用于统计。所有三种方法在SNR＜-5 dB时性能均急剧下降，在干扰恶劣的条件下定位效果有所欠缺。传统的MFP 显示出最差的定位精度，在高信噪比下仅有接近60%的定位准确率；CMFP 的性能稍好，但由于网格失配，很难获得理想的定位精度；OG-CMFP 的声源定位结果最佳，在SNR＞0 dB 的条件下实现了95%以上的定位准确率。

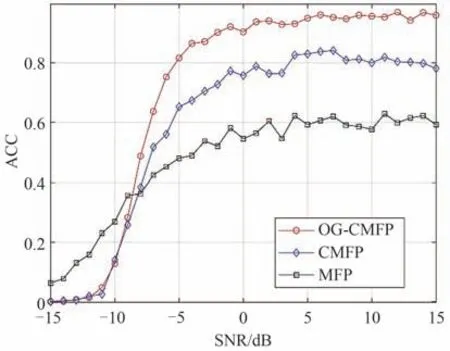
图4 双源平均定位准确率Fig.4 Average localization accuracy of two sources

三种方法在不同SNR下的双源平均rMAE如图5所示。随着信噪比的逐渐升高各类方法的距离定位误差逐渐减小，但传统MFP 即使在高信噪比条件下仍然表现很差，在多源定位任务中MFP 存在较多干扰峰极大地影响定位性能。CMFP 则给出了可接受的单频定位误差，但定位性能仍存在较大的提升空间。当SNR＞-5 dB 时，CMFP 的平均距离估计误差为337 m，而在相同条件下OG-CMFP 的定位误差为85 m，取得了最优的定位结果，验证了本文所提出方法的优越性能。

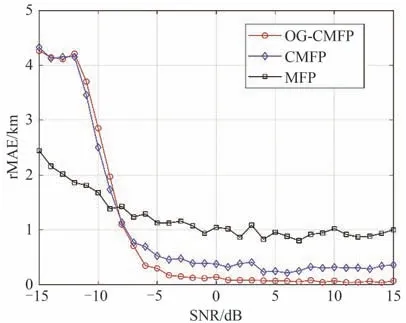
图5 双源距离平均绝对误差Fig.5 Average rMAE of two sources

由于实验中使用的网格划分较粗，为了探究网格深度间距对算法定位性能的影响，固定距离间隔不变，将深度间隔调整为1 m，使用相同的指标来进行对比，实验结果如图6 所示。可以看到在精细的深度网格划分下，MFP 和CMFP 的定位性能均有所提高，而OG-CMFP 由于细网格中字典元素相关性增大对群稀疏恢复存在一定影响，导致定位性能略有下降。图6（a）显示出OG-CMFP 在SNR＞0 dB 时实现了约93.5%的定位准确率；从图6（b）中分析可知当SNR＞-5 dB 时，CMFP 的双源平均距离估计误差为243 m，相较于MFP 和CMFP，OG-CMFP 的定位性能达到最优，其定位误差为109 m。因此，在细网格条件下本文提出的OG-CMFP 较传统方法仍具有明显优势，能够得到可信的定位结果。

图6 深度间隔为1 m时的定位结果Fig.6 Localization results at a depth interval of 1 m

为了探索声源的不同距离和深度对算法定位性能的影响，固定SNR=5 dB，变化距离和深度的所处范围来进行双源定位实验。这里设置了两种情况进行对比，一是在目标区域中限制不同距离的选取范围为ri=j±0.5 km，j=1，2，…，9，而深度可以随机选取；另一种是限制不同深度的选取范围为di=k±20 m，k=20，60，…，180，距离则进行随机选取。实验的双源距离平均绝对误差如图7 所示。图7（a）的实验结果表明不同声源距离对定位结果的影响较大，三种方法的误差均随距离的增加呈下降趋势，在近距离处的性能表现较远距离处更差，其中MFP 和CMFP 的定位精度对不同声源距离比较敏感，在近距离处易得到错误的定位结果。而OG-CMFP具有很好的鲁棒性，在整个目标区域内均能实现稳定并准确的声源定位。从图7（b）中可以看出，不同声源深度对定位结果的影响较小，相较而言声源深度在水域中段处的精度略低于两端处的精度。总体来看OG-CMFP 在不同的距离和深度条件下均呈现出最佳的性能。

图7 不同距离和深度的声源对定位精度的影响Fig.7 Effect of sources at different distances and depths on localization accuracy

5 结论

本文针对离网格水下源定位问题，通过将目标所处区域网格化，结合水下相邻位置处信道响应的高相似性，基于网格点处拷贝场向量的线性拟合建立可表征任意位置的拷贝场向量字典，从而构建了一种面向高精度定位的群稀疏离格信号模型，并提出了一种基于群稀疏优化的离网格压缩匹配场处理算法。实验结果表明，本文所提方法对不同距离和深度的声源能得到最佳的定位结果，同时在不同网格间距下均能实现准确定位。当网格的距离间隔为0.05 km、深度间隔为10 m时，在SNR＞-5 dB的条件下，OG-CMFP 表现出优异的性能，其双源平均测距误差与CMFP相比降低了250 m以上。