宽带高阶子空间超短基线水下声学定位

杨 磊 黄俊达 姜龙玉

（1.东南大学影像科学与技术实验室，江苏南京 210096；2.安徽工程大学可重构与智能计算实验室，安徽芜湖 241000）

1 引言

对水下作业的拖体（水下滑翔机、声呐等）进行精确定位时，根据基线长度的不同以及工作原理和作用范围的区别，可以分为长基线（Long Baseline，LBL）、短基线（Short Baseline，SBL）和超短基线（Ultra-Short Baseline，USBL）3种定位技术［1-3］。由于超短基线具有轻便性，且装卸方便，故越来越多的水下潜器选用超短基线作为其声学定位设备［4-6］。超短基线利用各个阵元接收信号间的时延与相位差来解算目标的方位和距离。但由于超短基线基阵孔径过小［7-9］等问题，导致水下目标定位误差项过大，因此需解决其误差问题从而提高水下目标定位的精度。

对于超短基线系统，根据发射声波信号形式的不同，可以将求解声线入射角的方法分为两类：基于窄带信号的相位估计方法和基于宽带信号的时延估计方法［10］。对于窄带信号相位估计而言，由于其信号信息带宽小，携带的信息量严重受限，从而导致对噪声的鲁棒性较差，且会出现相位模糊问题，需要采用额外修正措施，这也逐步淘汰了窄带信号作为信息传输媒介。而基于宽带信号的时延估计方法通过测量两个阵元接收信号的时延差来获取信号波达信息，可以有效避免相位模糊问题，同时宽带信号带宽较大，携带信息量充分，抗噪声干扰性强。其中，广义互相关 （Generalized Cross Correlation，GCC）法是基于时延估计的经典方法［11］，其可通过调整加权函数来增强信号中高信噪比频率的作用，从而提高估计精度，但在低信噪比下时延估计误差较大。XU等人［12］提出的重复广义互相关时延估计方法，先通过一次信号自相关来抑制噪声对定位精度的影响，然后再进行互相关操作，选取合适的加权函数可以较大程度提高水下源定位精度。VERA-DIAZ 等［13］提出将广义互相关时延估计方法与深度卷积神经网络相结合，通过构建三维声学图谱来估计源的相对位置，可以降低对预训练参数的要求，但是计算复杂度相对增加，同时也无法完全摆脱对环境参数的预估计要求。更重要的是，此类基于宽带信号的测时误差会与系统的采样率直接相关，这对于真实海洋环境往往是不小的挑战，同时阵列孔径过小也将直接导致阵元间的时延误差项过大。而与之相反的是，如果能够直接对目标相对于基阵的方位角和俯仰角进行估计，既可避免相位估计方法中的收敛速度和相位模糊问题，也可解决阵列孔径过小而导致时延估计精度过低等问题。

对此，本文拟将目标的定位问题转换成波达角的估计问题。最经典的阵列波达（Direction of Arrival，DOA）估计算法将属以MUSIC［14］为代表的特征子空间类算法。其通过对阵列接收数据做特征值分解，以此将原始接收数据划分为两个相互正交的子空间：与原始发射信号相一致的信号子空间和与噪声相对应的噪声子空间。然后根据两个子空间的正交特性，以信号子空间代替原始接收数据，构造出“针状”空间谱峰，在降低算法计算复杂度的同时，还提高了算法对于密集角度的分辨率。ZHENG 等人［15］将MUSIC 算法推广到对信号发射角和到达角的二维联合估计。而后JIANG 等人［16］提出了针对宽带相干信号分离的Smoothing MUSICAL算法，有效降低了宽带信号多频影响。在此基础上，JIANG等人进一步结合发射角、到达角以及传播时间的多维联合估计，利用四阶累积量矩阵替换传统协方差矩阵，提出了4-double-MUSIC 算法［17］，提升了浅海环境下对有色噪声的鲁棒性。BECKER等［18］通过对二阶、四阶累积量的精度变化趋势研究，发现DOA 的估计精度随着累积量的增长而提高，因此提出一种2q-MUSIC 算法，其将累积量向更高阶扩展来提高估计值精度。更重要的是，HE等［19-20］指出了高阶累积量能够实现虚拟阵列扩展，达到阵列孔径增大的目的，从而有效提升目标值的估计精度，这对于本文研究的小孔径超短基线阵列而言具有重要意义。

此外，由于海洋环境复杂多变，超短基线阵列会出现运动姿态跳变频繁，从而导致水下目标定位精度不足等问题。1960 年，R.E.Kalman［21］首次提出卡尔曼滤波，它通过不断预测、修正递推过程，可随时计算最新的滤波值，便于实时处理观测数据，提供一种最优估计值。近年来，许多学者以超短基线应用场景为基础，结合卡尔曼滤波技术，以此研究超短基线的实时定位方法。LUO［22-23］等人利用非等距四元阵列，对阵元接收到的声信号以卡尔曼滤波进行后处理来降低噪声，同时消除相位模糊问题，提供了高精度的相位差估计值。但卡尔曼滤波要求动力学模型、量测噪声和系统噪声的统计特性精确并且为已知值［24］，但在实际环境中很难满足上述要求。而自适应卡尔曼滤波［25］可在观测过程中连续根据当前观测值来估计并及时校正噪声统计特性、动力学模型等参数，从而有效降低了数据失真等对于定位精度的干扰，为水下动态目标高精度定位与跟踪提供新的技术支持。

综上，本文以海洋实际需求为目标，针对现有超短基线算法因阵列孔径过小而导致精度低、抗干扰性差等问题，提出了一种基于超短基线阵结构的宽带高阶子空间算法。理论与仿真实验表明，本文提出的算法可有效解决水声信号带宽大、相干影响以及海洋有色噪声环境导致的定位失准问题。同时，在此基础上引入自适应卡尔曼滤波算法，解决了传统卡尔曼滤波只针对线性高斯情况的局限和海洋移动目标定位出现异常点的问题。

2 算法原理与基础

2.1 定位原理

超短基线定位可利用水下源信号到达各阵元的时延差来计算对应的俯仰角和方位角，并通过测量声波的传播时间来计算源斜距。最后利用上述结果进行三角变换得到水下源的相对位置。本文提出的在等距四元十字阵列下的超短基线定位方法，其定位原理如图1所示。

在图1 的基阵结构基础上，假设信号源S 位于三维空间[x，y，z]处，相对于基阵原点的俯仰角和方位角分别为θ和φ，通过对基阵中每一个阵元的输出信号进行N点采样，其接收信号模型可表示为：

上式（1）中M为水听器数量，在本文中M=4，代表由4个水听器结构组成的基阵模型，am(θ，φ)表示对应于第m个阵元的阵列响应矢量。si(t)表示第i个声源发射的原始宽带chrip信号，fb为信号起始频率，k表示调频斜率，可由宽带信号带宽和信号时长确定。假设X(t)=[x1(t)，x2(t)，…，xM(t)]T为阵列接收矩阵，定义矩阵A为本文阵列的阵列流形，其中A=a(θ，φ)=[a1(θ，φ)，a2(θ，φ)，…，aM(θ，φ)]T，如果用S(t)表示原始发射信号矩阵，N(t)=[n1(t)，n2(t)，…，nM(t)]T表示噪声矩阵。则上式（1）的矩阵形式为：

针对式（2）中的阵列信号接收模型，可通过调节信号与噪声的比重（信噪比），来调控接收信号X(t)的质量。在水声领域，衡量信噪比主要有两种方式：带限信噪比和谱级信噪比，其中，带限信噪比容易出现伪值的情况，导致真实的信噪比与理论设计不相符。对此，本文采用式（3）所述的谱级信噪比来推算噪声的能量分布，再根据能量分布产生对应的噪声矩阵，以此保证信噪比真实值与理论值的一致性。

其中，Ps表示信号功率，由输入离散信号的均方根决定，E(n)表示噪声能量，B表示信号带宽。根据式（3）可获得如式（4）所示的噪声能量分布。

按照式（4）中的能量分布构建噪声矩阵N(t)即可获得对应的接收噪声信号模型。

对于图1中所述的超短基线阵列结构，无法直接表达其对应的阵列流形，也就是阵列流形矩阵A无法直接表达，因此必须将该阵列结构进行近似处理。为将只适用于平面波下的MUSIC算法扩展至三维声源定位场景下，本文将四元十字基阵按三维空间中的任意阵列结构［26］进行处理，将一维DOA 估计向二维联合DOA估计扩展，其阵列流形可表示如下：

其中，[xm，ym，zm](m=1，2，…，M)表示第m个阵元对应的位置，λ表示发射信号波长。针对单声源，根据式（5）中阵列流形，将四个阵元的已知坐标系位置代入可得其基阵的具体阵列流形，然后带入到式（2）的信号模型中进行三维空间下的声源位置估计。

由此，上述需要处理的超短基线定位问题即可转换为通过接收数据来估计信号波达的俯仰角和方位角问题。本文利用空间谱估计理论，以空域-频域平滑技术的MUSIC算法为依托，打破传统MUSIC算法计算量大、对于相干及小信噪比信号无法分辨等局限，从而提高定位的精度和算法的实时性。但由于MUSIC 算法本身具有的信号窄带化限制，对于本文的宽带信号无法直接进行估计，需要采用宽带预处理操作。同时，考虑到本文阵列结构孔径过小，直接使用现有的基于时延差、相位差的超短基线定位方法精度明显失衡，而基于二阶累计量的MUSIC 算法定位分辨率也存在不足。所以本文以高阶累积量代替传统超短基线阵列处理方法，使其对原始阵列结构进行虚拟扩展，提高阵列孔径，抑制海洋中的有色噪声影响，从而提高本文算法的定位精度。

2.2 卡尔曼滤波

传统基于MUSIC 的改进算法可以估计目标的静态位置，但由于目标的运动和洋流的影响会导致位置变化的异常，因此需要采取辅助措施来校正动态目标的定位。标准卡尔曼滤波（Kalman Filter，KF）［27-30］使用噪声的统计特性，将系统观测量作为输入，将要估计值的参数或系统状态作为输出，根据时间更新和观测更新算法估计出所需信号，可以有效去除部分异常对最终定位结果的干扰。假设离散线性系统方程和观测方程分别为：

其中，Xk可看作目标位置的状态向量，Φk，k-1是状态转移矩阵。ωk-1则是基阵的系统噪声向量。在观测方程中，Hk为观测矩阵，νk则为观测的噪声向量。ωk-1和νk为互不相关的零均值高斯白噪声，其协方差分别为Qk、Rk。KF 分为预测和更新两个阶段，如图2所示。

图2 卡尔曼滤波的预测和更新阶段图Fig.2 Diagram of the prediction and update stages of the Kalman filter

在更新阶段，计算卡尔曼增益，更新状态估计、误差协方差和噪声协方差矩阵，并利用当前位置的测量值对估计值进行优化。

在上式的方程中，Kk为卡尔曼增益矩阵，是估计状态，Pk是对于估计状态的协方差矩阵，I是单位矩阵。而从预测和更新阶段可以看到，卡尔曼滤波要求动力学模型、观测噪声和系统噪声的统计特性精确并且为已知值，但在实际应用中很难满足此要求，对此，本文融合自适应卡尔曼滤波（Adaptive Kalman Filter，AKF）的动态模型来解决定位值失真问题。

3 宽带高阶子空间超短基线定位技术

3.1 静态目标定位

为了解决上述研究中超短基线定位方法中涉及到的宽带信号和定位分辨率限制问题，本文提出了一种基于宽带高阶子空间的超短基线定位方法。该方法主要分为三步：1）按照2.1构建超短基线阵列信号接收模型；2）利用四阶累积量［31-32］代替传统协方差矩阵，通过改进的二维联合子空间估计方法，融合空域-频域平滑［16］处理，来解决由于多径传播性质，导致信号和噪声相干，引起秩亏损的问题；3）根据各阵元接收信号与原始发射信号之间的频谱分布关系，联合匹配滤波（Matched Filtering，MF）［5-6］算法获得水下声源相对于阵列几何中心的斜距。

在本方法的步骤二中，由于MUSIC 为典型的窄带信号处理方法，因此需要对本文的宽带阵列接收信号模型X(t)进行预处理。根据相干信号子空间（Coherent Signal-Subspace Method，CSM）算法［33-34］，宽带信号可以看作多个不同频率的窄带信号在频域信息上的组合，因此，考虑以聚焦变换的形式，使宽带信号各频率分量的信号子空间“聚焦”到参考频率的信号子空间，再对各频带的互谱密度矩阵进行频域平均来估计角度。其聚焦变换可表达如下：

式中，fj为带宽内任意频率，j为信号在频域下对应的某一频段数；f0为参考频率，即聚焦频率。则对应聚焦后的阵列接收信号矩阵为：

由上式可知聚焦变换后，各频率点下的聚焦矩阵所包含的频率信息相等。因此，可对聚焦后阵列各频率点的协方差矩阵求和平均。所以，现在所有的问题关键就在于如何构造适当的聚焦变换矩阵T。根据式（10）可知，对于宽带信号频域内的任意频率点，如果聚焦转换后的阵列接收信号与转换前的阵列接收信号尽可能一致，那么对于后序定位操作的精度影响就会更小。根据这一思想，上述式（10）中对应每一频率点的阵列流形与参考频率点对应的阵列流形需满足下述的约束条件：

在式（11）中，||.||F表示Frobenius范数，对于该优化问题，KAVEH［35］给出了满足此约束条件的最佳范数解：T(fj)=V(fj)U(fj)，其中V(fj)和U(fj)分别为矩阵A(fj)AH(f0)的左奇异矢量和右奇异矢量为列向量构成的矩阵。

求出聚焦变换矩阵T(fj)后，带入式（10）后可得到聚焦后的阵列接收信号X(fi)'。对聚焦阵列接收信号进行傅里叶变换后，其接收信号在频域下的大小为M×F，F为傅里叶变换频点数。然后如图3所示，截取分段数据大小为MS×FS，将子数据转换为一个长向量，再求对应的四阶累积量Ci，j，假设共有Kr×Kf个数据子块，故可以计算得到Kr×Kf个四阶累积量，求和之后进行平均，得到最终的四阶累积量C：

图3 四阶累积量的空域-频域平滑示意图Fig.3 Schematic diagram of spatial-frequency domain smoothing of fourth-order cumulant

其中，.*表示伴随矩阵，⊗表示Kronecker 积，.H 表示共轭转置。式（12）进行空域-频域平滑后得到的每个四阶累积量大小为(MS×FS)2×(MS×FS)2。对比直接求解C的大小为(M×F)2×(M×F)2，大大减小了矩阵维度，有效利用了内存空间，提高了计算速度。

上式平滑处理得到的四阶累积量，采用子空间方法可分解为信号子空间CS和噪声子空间Cn，即C=CS+Cn，进行特征值分解后，可提取噪声子空间Cn，那么基于高阶累积量的宽带MUSIC 算法的谱峰函数为：

再按照式（14）对谱峰进行二维联合搜索，峰值对应的方位角和俯仰角即为水下源目标的方位角、俯仰角估计值。

根据上述步骤可估计出水下目标的角度信息，可以大致确定了目标在水下的具体方位，但是无法确定目标的具体坐标，因为缺少必要的斜距信息。因此，在方法的第三步，就是对水下源斜距的计算。根据式（1）的接收信号模型可知，表达的接收信号中不仅仅包含了水下目标的方位信息，同时还包含了信号在传输过程中的时间信息。基于此，本文通过剥离该时间信息来实现信号在水下传播距离的计算，即水下源斜距的表达。通过对发射信号si(t)与阵元接收信号xm(t)之间实施匹配滤波操作，最终可以估计出信号从发射到接收在水下传播的时间t。考虑与时间序列相对应的采样数信息，那么上述的发射信号si(t)可表达为si[n]，接收信号可表达为xm[n]，其中n表示与时间信息相对应的采样数。对发射信号si[n]与第m个阵元的接收信号xm[n]做卷积运算：

综合所有阵元的卷积结果，得到信号能量相对于采样数的频谱分布：

扫描式（16）中频谱分布，峰值对应的横坐标值n即为信号在水下的传播时间对应的采样数，那么水下源斜距Rd可通过式（17）获得。

其中，v表示水下声速，fs表示采样频率。

综上所述，根据式（14）中的方位角和俯仰角估计值，以及式（17）中的斜距估计值，即可确定水下目标源的唯一位置。所以，本文提出的基于宽带高阶子空间的超短基线静态定位方法过程可描述为：

3.2 动态目标定位

当前结合超短基线定位系统的水下滑翔机等，由于存在姿态运动，会导致静态定位方法的效果不理想。而卡尔曼滤波器是一种高效率的递归滤波器，能从一系列不完全及包含噪声的测量中，估计出动态系统的状态，可用于海洋水下目标实时动态定位。但从2.2节中的预测和更新阶段可以看到，KF要求动力学模型、观测噪声和系统噪声的统计特性精确并且为已知值，这在实际运用中面临巨大挑战。为破除该局限，本文在静态定位的基础上，提出基于自适应卡尔曼滤波（AKF）［36-37］的宽带高阶子空间超短基线定位算法。其中的AKF 是一种递归定位方法，它本质上是一个预测和修正的过程，是对KF的改进。

根据式（6）的离散线性系统方程和观测方程，引入数学参数rk，不同于KF，过程噪声协方差Qk和测量协方差矩阵Rk根据rk的迭代而改变。

上式中Ek是残差，使预测值更加贴合更新值，dk是正则化参数，由遗忘因子h(0 ＜h＜1)决定。通过rk的设置，更新阶段除了计算卡尔曼增益、状态更新估计、估计协方差矩阵外，也对系统过程协方差矩阵和测量协方差矩阵进行迭代更新。其更新阶段的公式由于rk的引入，变换为：

在以上过程中，测量值以宽带高阶子空间静态定位算法进行测量。AKF 可以利用最新测量值对系统的观测噪声协方差矩阵和系统噪声协方差矩阵进行实时的自适应调整。利用遗忘因子来限制卡尔曼滤波器的记忆长度，充分利用现有的测量数据，去除异常数据，得到更精确的目标定位估计值。基于自适应卡尔曼滤波的高阶宽带子空间的总体流程如图4所示。

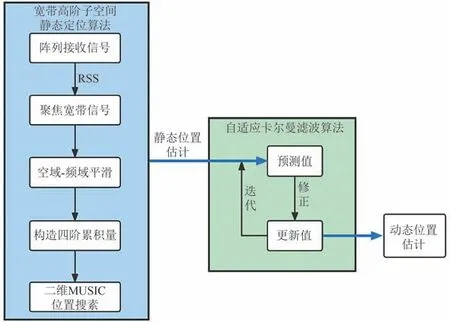
图4 基于AKF的高阶宽带子空间算法动态目标定位流程Fig.4 AKF-based higher-order wideband subspace algorithm for dynamic target localization process

4 实验结果

4.1 实验数据

为验证提出算法是否达到预期的定位效果，本文进行了相关水下环境的模拟实验。发射端由近水面超短基线系统中的声学换能器构成，位于基阵中心的声学换能器向水下装备应答器的航行目标发送定位脉冲信号，应答器接收到来自换能器的信号后回送一个定位信号进行处理。超短基线基阵的阵元间隔为入射信号波长的一半，由四个阵元组成等距十字阵列，从而形成一发射四接收的超短基线基阵。实验中采用如式（1）所述的线性调频信号（chirp）作为发射脉冲，信号中心频率13.5 kHz，水中声速为1500 m/s，采样频率为200 kHz。快拍数为300，信号带宽为3 kHz，频段范围为12 kHz至15 kHz。

4.2 性能指标

在静态目标定位场景下，引入准确率来判断本文提出方法的定位效果，准确率即为预测正确的样本数除以总样本数所得到的值。本文实验中，准确率的计算需结合式（20）所述的误差测量规则，将三维定位误差均保持在0.2%斜距以内的样本判定为预测正确样本，反之判定为错误样本。除准确率外，对于定位估计结果相对于理论值的偏移，能看到水下声源定位模型的细节，为此引入误差测量统计。一般，超短基线定位系统以相对误差进行结果度量，即以三维坐标位置误差与斜距之比表示，以X轴为例，其定义如下：

在动态目标定位场景，根据目标运动轨迹，则以估计值和真实值的误差进行测量，以Nu次实验的均方根误差（Root Mean Squared Error，RMSE）作为评价指标。其定义如式（21）所示。

4.3 实验结果与分析

4.3.1 宽带高阶子空间静态定位实验

为验证宽带高阶子空间算法对于超短基线定位的有效性，本节进行数据仿真实验，以相对于超短基线基阵坐标系［600 m，800 m，1200 m］处设置声源及应答器，转换成对应的方位角和俯仰角分别为53.1301°和39.8056°，源斜距理论值为1562.05 m，红噪声信噪比为5 dB 情况下的定位效果和斜距估计结果如图5所示。

图5 本文算法定位效果与斜距估计结果Fig.5 Localization effect and slant distance estimation results of the algorithm in this paper

根据图5 的角度估计与斜距估计结果，定性分析，在图5（a）中，算法频谱分布平滑，峰值明显，无伪峰干扰，分辨率高。图5（b）中，信号能量分布明显，斜距采样数对应的峰值突出。定量分析，算法估计的方位角、俯仰角分别为53°和40°，较理论值具有很高的估计精度，且当前实验设置的角度扫描间隔为1°，可以在保证定位精度的同时，降低角度空间的扫描时间复杂度。图5（b）中斜距对应的采样数n为208500，按照式（17）估计的斜距为1563.75 m。最后将估计值转换到三维坐标空间：。根据式（20）计算出三个坐标维度相对于斜距的误差项分别为0.3%、0.17%、0.13%，由此可以看出，本文提出的基于宽带高阶子空间的超短基线方法不管是在定位效果方面，还是在定位精度方面，均具有较好的表现。

更进一步，因为本算法是将源定位问题转换成了高阶波达角（DOA）的估计问题，也就是说高精度的DOA估计是良好定位效果的保障。对此，本文将提出算法的DOA 估计精度随信噪比的变化趋势做了详尽的对比与分析，变化曲线如图6所示。

图6 两种子空间方法在不同信噪比下的DOA估计误差曲线Fig.6 DOA estimation error curves of two subspace methods under different signal-to-noise ratio

根据图6（a）、（b）所示的两种子空间算法在不同信噪比环境下的DOA估计误差分布可以看出，本文提出的宽带高阶子空间算法不管是在何种条件下，对应的方位角和俯仰角估计误差均保持在0.3°以内。而传统的二阶子空间算法，在较低信噪比条件下DOA误差可达0.9°。由此可知，本文提出的算法在DOA估计精度上有明显的改善，在低信噪比环境下改善效果尤为明显，这也凸显了本文提出的定位算法具有较好的有效性和可行性。高精度的DOA 估计可以减小后续定位的累积误差，从而从整体上改善水下声源的定位精度。

此外，为了探究本文提出方法的优越性，对阵列接收数据在不同信噪比下添加了高斯白噪声和色噪声进行对比实验，每一组实验通过20 次门特卡洛实验取均值，保证了结果的合理性，得到准确率结果如表1、表2 所示，定位精度结果对比如图7、图8所示。

表1 不同定位方法在不同信噪比高斯白噪声下的准确率Tab.1 Accuracy of different localization methods under Gaussian white noise with different signal-to-noise ratios

表2 不同定位方法在不同信噪比红噪声下的准确率Tab.2 Accuracy of different localization methods under red noise with different signal-to-noise ratios

图7 不同定位方法在不同信噪比红噪声下的定位相对误差曲线Fig.7 Localization relative error curves of different localization methods under different signal-to-noise ratio red noise

图8 两种子空间方法在不同信噪比红噪声下的定位相对误差曲线Fig.8 Localization relative error curves of two subspace methods under different signal-to-noise ratio red noise

由表1 和表2 的对比可看出，相对于基于时延的GCC 和GCC-PHAT 算法，2 阶MUSIC 算法和本文在此基础上提出的宽带高阶子空间算法的定位准确率明显更高，且无论在高斯白噪声还是在红噪声环境下，都有较好的定位准确度。除此之外，本文提出的宽带高阶子空间算法对于红噪声的鲁棒性明显高于前两种算法，与2 阶MUSIC 相比，在低信噪比环境下有更好的定位准确率。即使在-20 dB环境下，定位准确率也领先2 阶MUSIC 算法20%以上。图7（a）、（b）、（c）分别描述了上述四种不同方法在不同信噪比情况下，以红噪声为背景的定位相对误差。从图7 可以看出，子空间类算法定位相对误差远小于同等参数配置下的GCC 算法和GCCPHAT 算法。而本文提出的宽带高阶子空间算法在低信噪比下的定位误差相对于2 阶MUSIC 算法表现更好，误差值均小于其他几种对比方法。为更直观显示其定位误差区别，截取了两种子空间类方法进行单独对比，其定位误差结果如图8 所示。从实验结果可以看到，本文提出的宽带高阶子空间算法总体定位误差更小，性能更加稳定，对噪声的鲁棒性也更好。

4.3.2 自适应卡尔曼滤波高阶子空间动态定位实验

本节实验中，为模拟目标运动状态下本文提出算法的定位效果，模拟仿真三组数据，分别是深度为0 m 的近水面圆周运动，深度为500 m 的水下圆周运动，以及深度从0 m 至500 m 的螺旋圆周运动。图9（a）、（b）、（c）分别描述了在信噪比为-15 dB 红噪声条件下，基于自适应卡尔曼滤波的子空间定位、基于常规卡尔曼滤波的子空间定位，以及宽带高阶子空间定位在这三组仿真数据的结果。为直观表示，取其一部分轨迹进行观察。

图9 三组仿真数据中不同定位方法的动态定位轨迹结果Fig.9 Dynamic localization trajectory results of different localization methods in three sets of simulation data

从图9可看出，在三组仿真数据中，本文提出的基于自适应卡尔曼滤波的宽带高阶子空间技术的动态定位表现结果优于其他两种对比方法，估计的运动轨迹更加平滑，且更贴近真实值。在低信噪比红噪声条件下，可以看到基于常规卡尔曼滤波的子空间算法表现不稳定，对深度变化不敏感，而本文提出方法更具有精度优势，对红噪声表现出更好的鲁棒性。因此可说明本文提出的高阶子空间动态定位方法具有较好的实用性。

5 结论

本文提出了一种基于宽带高阶子空间的超短基线水下声源定位方法，这种方法相较于当前使用的时延、相位位置估计算法，能有效提高水下声源位置估计的分辨率，且在低信噪比环境下对噪声有较好的鲁棒性。同时本文提出的基于自适应卡尔曼滤波的宽带高阶子空间算法，能适应水下运动目标的定位场景，对比一些其他动态定位方法，本文方法动态定位效果更好，且能有效地处理宽频带信号信息，提高了动态目标的定位精度，提升了对噪声的鲁棒性。实验以更加贴合海洋真实环境的红噪声作为噪声项，体现了本文提出的静态、动态算法具有实用性和可行性。