PC-FFT：一种时频协同的差分水声OFDM 信号ICI抑制方法

李渝舟 黄运龙 桂正泰 周 闯

（华中科技大学电子信息与通信学院，湖北武汉 430074）

1 引言

差分正交频分复用（Orthogonal Frequency Division Multiplexing，OFDM）由于其在对抗频率选择性衰落和降低导频开销方面展现出的强大能力，成为实现高速水声通信的一种极具潜力的技术方案［1］。具体而言，一方面，OFDM 技术通过串并转换和添加保护间隔，可有效对抗水声信道大时延扩展引起的频率选择性衰落［2］，差分OFDM 技术继承了这一优势。另一方面，差分OFDM 技术通过引入差分编码，可以通过依靠相邻载波间（频域）或相邻符号间（时域）的相干性，在无须估计信道状态信息的情况下，以差分相干检测的方式恢复出原始数据符号，从而可大幅降低用于信道估计的导频开销［3-4］。

考虑在频域上差分编码的OFDM 系统，确保差分相干检测能准确恢复出原始数据符号的一个重要前提是相邻载波上的信道频率响应要尽可能接近，即载波之间具有较强的相干性。对于带宽B一定的OFDM 系统，可以通过增大载波数K来缩小载波间隔，从而增强载波间的相干性。另一方面，增大载波数也能提升系统的带宽效率，其中，Q和Tg分别是调制阶数和相邻OFDM 符号间的保护间隔长度。然而，缩小载波间隔Δf也会使得系统对频偏更加敏感，即在水声信道固有的强多普勒频偏的情况下，进一步加剧了系统的载波间干扰（Inter-Carrier Interference，ICI），使得接收信号难以被精准检测。因此，在差分OFDM 系统中，需要使用尽可能多的载波来确保相邻载波之间的强相干性和提升高带宽效率，同时也需要将ICI抑制到较低的水平。

针对OFDM 系统的ICI 抑制问题，国内外学术界已从不同的角度展开了大量的研究。基于多重快速傅里叶变换（Multiple Fast Fourier Transform，Multi-FFT）的一系列方法是其中的一类典型方法。根据作用域的不同，这类方法可分为时域类、频域类和时频域类这三个子类，分别以分段快速傅里叶变换（Partial Fast Fourier Transform，P-FFT）、分数快速傅里叶变换（Fractional Fast Fourier Transform，FFFT）和分段频移快速傅里叶变换（Partially-Shifted Fast Fourier Transform，PS-FFT）为代表。其中，PFFT最早应该是在文献［5］中提出，其将一个完整的OFDM符号持续时间均匀地划分为几个不重叠的短区间，以减小信号时变性；然后，对每个短区间内的接收信号分别执行傅里叶变换，在每个载波上产生多个解调输出；最后，再将这些输出线性加权为一路输出用于符号检测。文献［6］则最早将P-FFT 应用于差分OFDM 系统，并设计了一种基于梯度下降的算法来求解权重向量。此外，文献［7］将文献［6］中仅具有单个接收单元的差分系统扩展到配备有多个接收单元的系统。文献［8］中则设计了一种基于特征分解的权重求解算法，以避免梯度下降法对初始点和步长设置敏感的问题。F-FFT 最早在文献［9］中提出，其对接收信号按载波间隔Δf的多个分数倍频率进行频移，即多点频率补偿，然后分别执行傅里叶变换，最后将多个输出按和文献［6-7］中相同的方式加权合并为一路输出。文献［10］引入了梯度缩放和阈值控制机制来改进文献［6-7，9］中的梯度下降法。此外，文献［11］则设计了一种称之为判决分数快速傅里叶变换（Decision Fractional Fast Fourier Transform，DF-FFT）的方法，其通过符号重建的方式来提升F-FFT的性能。

相比上述从单一域抑制ICI 的P-FFT［5-8，10］和FFFT［9-10］等时域和频域方法，文献［12］中设计了一种称之为PS-FFT 的时频协同ICI 抑制方法。具体而言，首先，PS-FFT 在时域上将OFDM 符号持续时间划分成多个短区间，化快变信号为准静态信号；其次，在频域上对每一划分后的短信号按多个预先设定的频率进行频移，即多点频率补偿，其中补偿频率没有像F-FFT 那样限制成载波间隔Δf的分数倍，而是可以设置成任意基准偏移频率fe的分数倍；最后，将各补偿后的信号分别执行傅里叶变换，并利用基于梯度下降的算法［10］求解得到权重将多路输出合并为一路。基于上述做法，PS-FFT 同时兼具了时域方法和频域方法的优势，达到时频协同抑制干扰的效果，并通过大量测试结果验证了其抑制性能相比单域方法P-FFT［5-8，10］和F-FFT［9-10］的优越性。然而，由于PS-FFT 中也具有类似F-FFT 的将同一段信号按多个预设偏移频率进行补偿的做法，其可能会面临当多普勒频偏较大时，因权重求解不准导致的频率补偿过饱和的问题。具体而言，如果其中一个预设的补偿频率恰好等于或者十分接近多普勒频偏，则该路输出的信号中的频偏将被抑制得足够小。而其他路上的预设补偿频率由于与多普勒频偏之间存在差距，输出的信号中仍有较为明显的频偏。当权重求解不够准确时，即将几乎不含频偏的信号和有明显频偏的信号按不合理的权重做加权，那么加权后的信号中将仍含有不可忽略的频偏，甚至会加剧频偏。

针对上述问题，为进一步提升系统在大多普勒频偏下的检测性能，本文设计了一种称之为分段-单频率校正快速傅里叶变换（Partially-Single-Frequency-Corrected Fast Fourier Transform，PC-FFT）的时频协同ICI抑制方法。具体而言，PC-FFT 和PSFFT 类似，也是先在时域分割、再在频域补偿、最后线性加权。但所不同的是，PC-FFT在每个分段后的短区间内只做单频点补偿，且不预先设定补偿频率，而是动态优化得到。为了求解权重和补偿频率，建立了以二者为变量，以最小化信号检测均方误差（Mean Square Error，MSE）为目标的优化问题。鉴于在该问题中两个变量之间高度耦合导致的目标函数严重非凸，为降低计算开销，提出了基于坐标轮换下降的求解算法。仿真和实测水声信道的测试结果均表明，PC-FFT在大多普勒频偏场景下的检测性能要显著优于P-FFT、F-FFT和PS-FFT。

本文其余部分组织如下。在第二章中，本文介绍了差分水声OFDM通信的系统模型。第三章描述了本文设计的PC-FFT 方法的详细过程。仿真测试结果在第四章中给出，以验证所提出方法的性能。

2 差分水声OFDM系统模型

考虑一个具有如下参数配置的差分OFDM 系统：载波数为K、带宽为B、最低载波频率为f0和保护间隔为Tg，则系统的载波间隔为，OFDM 符号持续时间为，各路载波频率fk为

记搭载到第k路载波上的传输符号为dk，其由原始数据符号bk执行差分编码得到，如下所示

其中，符号bk通过对原始比特信息做Q阶能量归一化的相移键控（Phase-Shift Keying，PSK）调制得到，即bk属于星座集合A={a0，a1，a2，…，aQ-1}，aq=，q=0，1，2，…，Q-1。

对搭载到各路载波上的差分符号dk执行逆傅里叶变换，可得到基带时域信号s(t)，表示为

再对s(t)按最低载波频率f0进行上变频，可得到带通时域信号，如下所示

其中，Re{·}表示取复数的实部。

其中，hp(t)和τp(t)分别为各路径上的增益和时延，为噪声，为第k路载波上的信道系数。

首先考虑信道时不变的情况，即hp(t)和τp(t)不随时间t变化的理想情况。此时，Hk(t)退化成与时间t无关的量，从而式（7）中的积分项只包含，由于其具有如下正交关系

因此，在信道时不变情况下，式（7）可展开为

对相邻两路载波上的解调输出xk和xk-1执行差分相干检测，得到

当相邻两路载波上的信道响应Hk和Hk-1可以认为近似相等，以及噪声可以忽略时，式（10）展开为

即通过差分相干检测，利用载波之间的相干性，成功恢复出了发送符号bk。

然而在实际水下环境中，由于声波的缓慢传播特性，水声信道通常具有强烈的多普勒效应，导致信道快速时变。此时，Hk(t)无法退化成Hk，式（7）中的积分项也不再是，而是。由于积分项不满足式（8）所示的正交关系，从而推导不出式（9）所示的输入输出关系。事实上，当存在多普勒效应时，式（9）应重写成如下所示的形式

即按式（7）执行FFT 解调得到的xk中含有ICI。当ICI 达到不可忽略的程度时，按式（10）执行差分相干检测，将难以成功恢复出发送符号bk。

3 基于PC-FFT的时频协同ICI抑制方法

在本章中，首先描述了基于PC-FFT 的时频协同ICI 抑制方法的结构设计，然后建模了一个以权重和补偿频率为变量，以最小化信号检测均方误差为目标的优化问题，并结合仿真实例说明了其具有高度非凸的特点。最后针对该优化问题，为降低其计算开销，设计了一种基于坐标轮换下降的求解算法。

3.1 基于PC-FFT的ICI抑制结构

PC-FFT 方法的核心思想是先将一整个OFDM符号持续时间[0，T]内的接收信号划分为多段，由于划分后的短信号持续时间相比划分前的信号要短，因此更接近或者小于信道相干时间，即化快变信号为准静态信号，减小信号的时变性，从而在时域的角度缓解ICI。然后对每一分段之后的短信号分别按单个频率进行频移，补偿多普勒频偏，从而在频域的角度缓解ICI。其中，各分段上的补偿频率不是预先设定的，而是动态优化得到的。最后再对各补偿后的信号分别做FFT，并通过线性加权的方式将多路FFT 输出合并成一路。图1 展示了PC-FFT 方法的整体结构，下面具体介绍其步骤和细节。

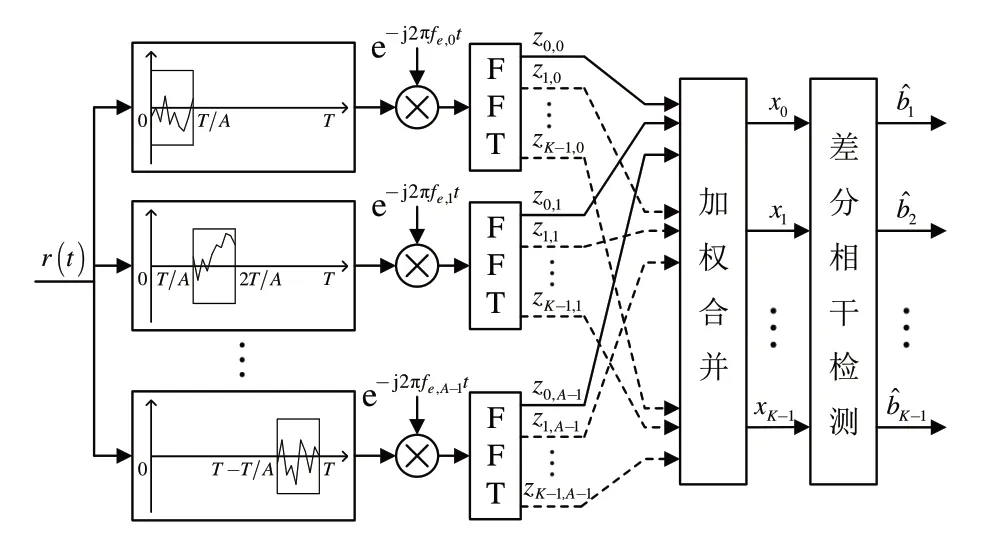
图1 PC-FFT方法结构框图Fig.1 Block diagram of the PC-FFT approach

如图1所示，首先，PC-FFT将基带接收信号r(t)均匀地划分成了A段互不重叠的短信号ra(t)，该过程可以通过将r(t)乘以一系列的非重叠矩形窗口函数来实现

其中，rect(t)为单位矩形窗口函数，仅当|t|≤0.5时函数值为1，其他情况下函数值为0。

接下来，PC-FFT对各路上的分段信号ra(t)分别按一个经优化得到的频率fe，a进行频移，表示为

然后，对上述得到的A个频移后的分段信号ra，fe(t)分别执行傅里叶变换，在每个载波处得到A个解调输出zk，a，其为

最后，将同一载波处的A个解调输出zk，a排列成列向量的形式，表示为

再用一个与解调向量zk相同维度的权重向量wk的共轭转置乘以zk，即对zk进行加权合并，得到各路载波上的最终解调结果xk，如下所示

对符号xk执行式（10）所示的差分相干检测得到符号检测结果。

3.2 优化问题建模

由式（9）可知，对于时不变信道，相邻两路载波上的接收符号xk和xk-1与发送符号dk和dk-1之间满足

当相邻两路载波上的信道响应Hk和Hk-1近似相等时，式（18）可以写为

其中，vk=nk-bknk-1为差分噪声，其方差是原始噪声nk方差的两倍。

由式（19）可知，发送符号bk的最大似然估计可表示为

进一步地，根据式（20），第k路载波上的符号检测误差可定义为

考虑在一个OFDM 符号上均匀地安插了KP个导频，则单个OFDM 符号的导频处总检测误差E可表示为

其中，KP是由KP个导频载波序号组成的集合。

为方便后文表述，记PC-FFT 方法中各路上的补偿频率组成的向量为

显然，由式（15）、式（16）、式（22）和式（23）可知，导频处的总检测误差E同时受权重向量wk和补偿频率向量fe的影响，二者的求解精度直接关系ICI的有效抑制程度。因此，本小节建立了以wk和fe为变量，以最小化E为目标的优化问题。为了直观地展示目标函数E的凹凸性，本文测试了E随补偿频率的变化曲面图，如图2 所示。其中，PC-FFT 的分段数A设置为2，即把原始接收信号r(t)分成了两段短信号r0(t)和r1(t)。r0(t)和r1(t)分别在频率fe，0和fe，1上做补偿。考虑到信道多普勒因子和中心载波频率分别为α=3×10-4和fc=32 kHz，对应中心载波上的多普勒频偏为fd=αfc=9.6 Hz，因此设置fe，0和fe，1均从-2fd到2fd范围内变化。此外，系统采用文献［10］中提出的基于梯度下降的算法求解权重向量wk。从图2 中，可以看出均方误差的曲面图呈现出高度非凸的特性，其很大程度由wk和fe高度耦合所导致。

3.3 权值和补偿频率的联合求解算法

考虑到如3.2 节所述，优化问题中权重向量wk和补偿频率向量fe之间高度耦合，致使其严重非凸，为降低求解复杂度，本节基于坐标轮换下降的思路，设计了一种wk和fe的联合求解算法。具体而言，在权重向量求解阶段，固定补偿频率向量不变，利用文献［8］提出的特征值分解法进行求解；在补偿频率向量求解阶段，固定权重向量不变，利用梯度下降法进行求解；二者依次交替执行，直至收敛。以下两个小节将先依次介绍wk和fe的求解算法，再由最后一个小节给出联合求解算法的整体结构设计。

3.3.1 基于特征值分解的权重求解算法

考虑到文献［6-7，9-10］中的基于梯度下降的算法以自适应的方式求解权重向量，其性能受起始点和步长等参数设置的影响很大，即鲁棒性较差，因此对于本问题中的权重向量求解，将采用文献［8］中提出的基于特征值分解的算法，以非自适应的方式求解权重向量。以下简要介绍这种算法的主要原理和步骤。

文献［8］首先考虑了当多普勒效应较小，重采样后的接收信号具有窄带特性的情况，此时可以认为各载波上的wk都近似相等，即

进一步地，文献［8］中也考虑了当多普勒效应较为严重，重采样后的信号仍具有宽带特性的情况，即无法认为K个载波上的wk都近似相等。为此，相应的做法是将全部K个载波均匀地划分成了S个子区间，使得划分后的短区间具有窄带特性，从而可以认为每一子区间内的个载波上的wk都相等，即

其中，0 ≤s≤S-1为分区间的序号，ws，k'为第s个子区间上第k'个载波的权重向量，0 ≤k'≤。特别地，当S=1时，即对应没有划分子区间的情况。

由式（21）可知，第s个子区间上个导频载波处的总符号检测误差Es表示为

其中，KP，s为第s个子区间上的个导频载波序号组成的集合为第s个子区间上的导频检测误差矩阵。显然，RP，s是一个厄米特（Hermitian）矩阵，即满足。

由此，将第s个子区间上权重向量的求解问题建模为

利用拉格朗日（Lagrange）乘子法，可以将式（27）中带约束的问题转换为一个无约束问题

求解L(ws)求关于ws的偏导数有

因此，对于式（29）中的偏导数为0 的极值点有以下关系

根据矩阵特征值分解的性质可知，满足式（30）的λs和ws分别为方阵RP，s的特征值和其对应的右特征值向量。记方阵RP，s的最小特征值及其对应的归一化右特征向量分别为λs，min和vs，min，那么当ws取值为时，式（26）中的导频处总检测误差Es达到最小值

由此，文献［8］通过特征值分解，以非自适应的方式求出了各个子区间上的最优权重向量

3.3.2 基于梯度下降的补偿频率求解算法

如3.3.1 小节所述，在求解权重向量wk时使用到了在每个OFDM 符号上插入的KP个导频，为节省导频开销和提升频谱效率，本小节中也将复用这些导频来求解补偿频率向量fe。以式（22）中定义的KP个导频载波上的总检测误差E为目标函数，为使用基于梯度下降的算法优化fe，需求解出E关于fe的偏导数。

首先，由式（22）和式（23）可知，E关于fe的偏导数可展开为

因此，这里先求解出单个导频载波上的检测误差|ek|2关于单个补偿频率fe，a的偏导数，经数学推导可得到该求导结果为

结合式（33）和式（34）中的关系式，可得到总检测误差E关于fe的偏导数的最终求解结果为

其中，运算符Im{·}表示取复数的虚部，并涉及到以下符号记法

其中，运算符∘表示两个相同维度的向量或矩阵之间的哈达玛（Hadamard）积。

最后，取式（36）所示的求解结果的相反数即为目标函数E关于fe的梯度，表示为

由此即可按梯度下降的方式迭代地求解fe，如下所示

其中，μfe为步长系数，iter为迭代次数的索引。

3.3.3 联合求解算法整体结构设计

图3为本小节设计的基于坐标轮换下降的联合求解算法的整体结构框图。该联合求解算法按逐OFDM 符号的顺序求解权重向量wk和补偿频率向量fe，并分别采用3.3.1和3.3.2小节中所描述的算法求解wk和fe。以下具体介绍该算法的执行过程。

图3 权重和补偿频率的联合求解算法框图Fig.3 Block diagram of the algorithm for jointly solving the weight and compensation frequency

首先，算法设置了一个补偿频率向量的初始值fe，init，作为第1 个OFDM 符号上fe迭代的起始值，即，并用该起始值对r(t)和tr(t)分别执行PC-FFT 解调得到zk和。紧接着，利用zk和导频信息进行基于特征值分解的权重求解，得到wk的第一轮求解结果。接下来，利用分别对zk和执行加权合并和Hadamard 乘积运算得到xk和。然后，再利用xk和，以及导频信息进行基于梯度下降的补偿频率求解，得到fe的第一轮求解结果，完成联合求解的第一轮循环。

考虑到相邻OFDM符号上的多普勒频偏通常较为接近，为降低迭代次数，因此从第2个OFDM 符号起，是将当前OFDM符号上fe迭代的起始值设置为上一个OFDM 符号上的fe迭代的终止值，即，其中n≥2 为OFDM 符号序号的索引。算法1中总结了该联合求解算法的详细执行步骤。

此外，考虑到基于梯度下降的补偿频率向量求解算法对于初始点十分敏感，为提高算法的鲁棒性，本文设计的算法也采用了文献［13-14］中的假设检验法，作为联合求解前的预处理过程。具体而言，先按一系列预先设定的fe分别对第1 个OFDM符号执行PC-FFT 解调，并利用基于特征值分解的算法求出的wk对解调输出zk进行加权合并得到xk。然后对xk执行差分相干检测，并统计出第1 个OFDM 符号上导频处的总检测误差E。之后，找出使得E最小的预设fe，即为第1 个OFDM 符号上的fe的迭代起始值f1e(1)。

4 仿真实验与结果分析

本节基于两类水声信道分别进行了仿真实验，来测试本文所设计的PC-FFT 方法和现有P-FFT、FFFT、PS-FFT 方法，以及使用单路FFT 解调的无ICI抑制的方法（Single-FFT）的性能。第一个小节将介绍基于理论信道模型的仿真水声信道的实验，第二个小节将介绍基于Watermark 平台的实测水声信道的实验。其中，值得注意的是，在测试上述算法性能时，仅考虑其干扰抑制能力对信号检测的影响，并未考虑信道编解码、峰均比抑制等模块。

4.1 基于仿真水声信道的实验

本小节参照文献［6］中的差分水声OFDM系统的典型参数配置，结合基于理论信道模型的仿真信道，构建了仿真系统，来开展对PC-FFT等方法的性能测试。本小节将先介绍仿真系统的具体参数配置，然后展示用此参数配置获得的测试结果，并予以分析。

4.1.1 仿真参数设置

表1 总结了仿真系统的主要OFDM 参数配置，其中，载波数K和每帧包含的OFDM 符号数N之间满足KN=213的数量关系，即一帧所包含的QPSK符号数是固定为213。表2 总结了4 种ICI 抑制方法的参数配置，其中，P-FFT、PS-FFT 和PC-FFT 的分段数均设置为3，F-FFT 和PS-FFT 的补偿频率数均设置为3。此外，考虑到在本小节的仿真测试中，信道的最大多普勒因子为αmax=5×10-4，对应中心载波上的频偏为fd，max=αmaxfc=16 Hz，因此，在本小节中将PS-FFT 的基准偏移频率fe设置为fd，max的两倍，即fe=2fd，max=32 Hz。对于PC-FFT 方法，在联合求解前的假设检验阶段，则是从-32 Hz 到32 Hz 的范围内，以8 Hz 为间隔取出9 个频率分别对每帧的第1个OFDM符号进行预解调。

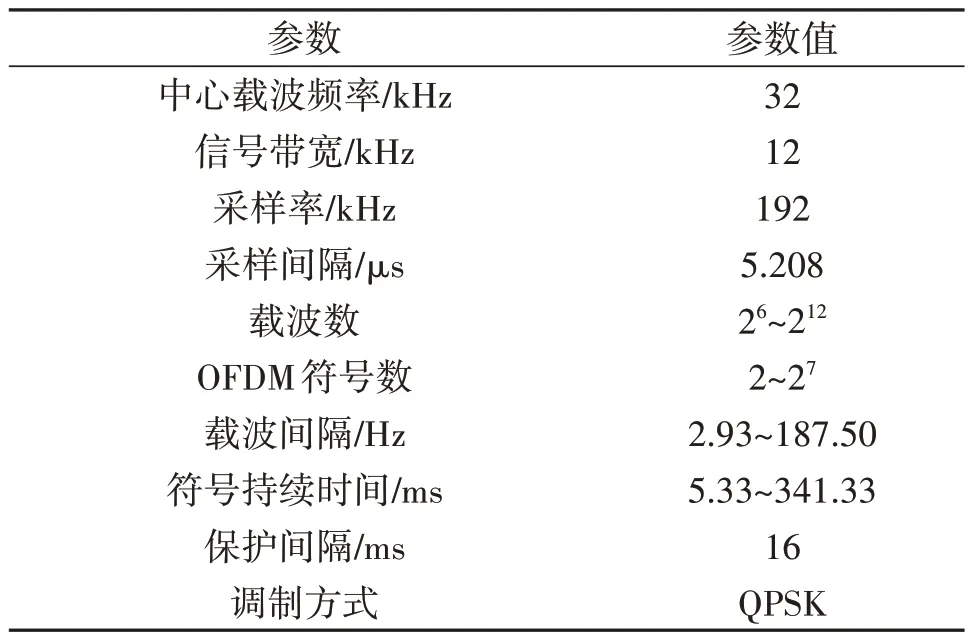
表1 基于仿真水声信道的仿真实验OFDM系统参数配置Tab.1 Parameter settings of the OFDM system in the simulation based on the simulated UWA channel

表2 基于仿真水声信道的仿真实验ICI抑制方法参数配置Tab.2 Parameter settings of the ICI mitigation methods in the simulation based on the simulated UWA channel

此外，如表2所示，为了公平起见，4种方法都是在每帧OFDM数据上插入了NP=256个导频。所不同的是，对于P-FFT、F-FFT 和PS-FFT，256 个导频是安插在每帧OFDM数据开头的256个连续的载波上，用于启动基于梯度下降的权重求解算法。根据载波数的不同，这256 个导频分布在第1 个或者前几个OFDM 符号上。而对于PC-FFT，是在每个OFDM 符号上都等间隔地安插了个导频，用于权重向量和补偿频率向量的联合求解。最后，如3.3.3小节中所述，在利用基于特征值分解的方法求解PCFFT的权重向量时，是将全部K个载波分成了S个子区间。其中，当K为64、128 和256 时，由于每个OFDM符号内的导频数KP较少，因此是将S都设置为1。当K为512、1024、2048 和4096 时，S分别设置为2、4、8和16，使得每个子区间内的导频数都为8。

表3中总结了仿真水声信道的主要参数配置，包括水深和收发机距离等几何参数，以及扩散因子和声速等物理参数。基于表3中的参数配置，使用文献［15］中提供的水声信道仿真器生成了本节所使用的仿真信道，其路径增益和时延分布如图4所示。

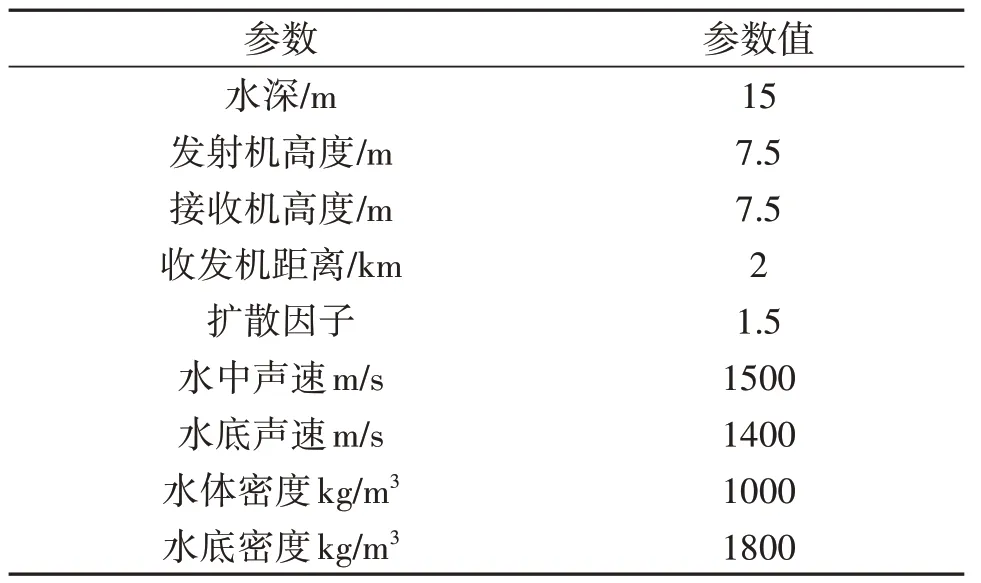
表3 仿真水声信道参数配置Tab.3 Parameter settings of the simulated UWA channel

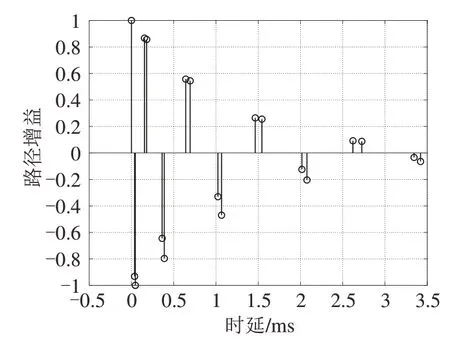
图4 仿真信道路径增益-时延分布图Fig.4 Path gains and delays distribution of the simulated UWA channel

4.1.2 仿真结果及分析

本小节首先测试了5种方法在不同多普勒因子α下的符号检测MSE性能，结果如图5所示，其中，多普勒因子α是在10-4～5×10-4的范围内变化，信噪比和载波数分别固定为SNR=10 dB 和K=1024。从图5中可以看出，当α较小时，5种方法都能比较好的工作，随着α增大，检测性能都在下降，这也从侧面体现了抑制ICI 的重要性。当α增长到2.5×10-4时，Single-FFT由于没有抑制ICI，其MSE达到了3.57 dB，对应的误比特率（Bit Error Rate，BER）为43.92%，接近50%的乱猜概率，即Single-FFT 此时已经几乎完全无法工作，而其他方法由于在不同程度上抑制了ICI，此时都能保持较好的性能。

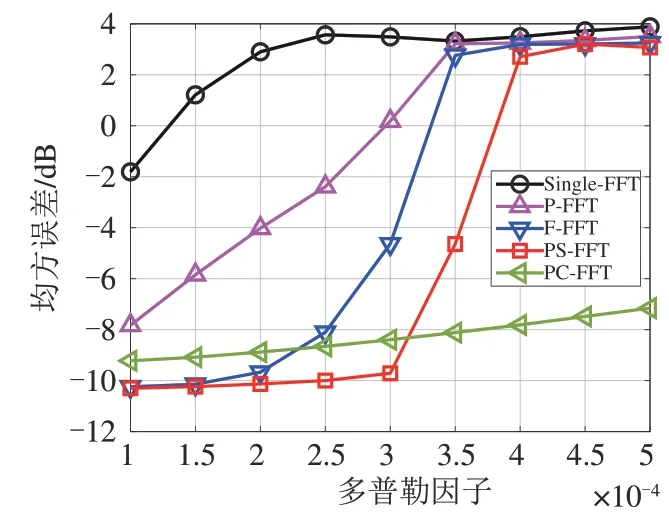
图5 不同多普勒因子下5种方法的MSE性能（基于仿真水声信道）Fig.5 MSE performance of five methods under different Doppler factors （based on the simulation UWA channel）

此外，从图5 中可以看出，对于3 种现有ICI 抑制方法，F-FFT 的MSE 性能要优于P-FFT，说明从频域抑制ICI 相比从时域抑制ICI 更为有效。更进一步地，PS-FFT的MSE性能要优于F-FFT，且随着α增大优势更加明显，说明协同时频域抑制ICI 相比从单域抑制ICI 能够取得更好的效果。对于PC-FFT，虽然当α较小时（例如10-4～2×10-4），其性能不及PS-FFT 和F-FFT。但当α达到2.5×10-4的时候，PC-FFT 的MSE 开始低于F-FFT 的MSE。当α超过3×10-4后，PS-FFT 的MSE 开始急剧攀升，并在α=4×10-4的时候，MSE 达到2.71 dB，此时对应的BER 为48%，非常接近50%的乱猜概率，即几乎完全无法正常工作。造成这一现象的可能原因是PSFFT没有显示地求解频偏，ICI抑制性能完全依赖于权重求解精度。当α较小时，使用梯度下降法可以较为准确地求解权重，因此能维持较好的性能。而当α较大时，权重求解精度急剧下降，频率补偿出现过饱和，进而检测性能显著下降。对于PC-FFT，由于显示地估计了频偏，在α达到3.5×10-4时，性能开始超过PS-FFT，并在α高达5×10-4时，仍能维持-7.15 dB的性能。

其次，本小节也测试了5种方法在不同载波数K下的符号检测MSE性能，结果如图6所示，其中，载波数是在64～4096的范围内变化，多普勒因子和信噪比分别固定为SNR=10 dB和α=3.5×10-4。此外，在图6中也测试了α=0，即没有多普勒效应时的Single-FFT 的性能，其随着K增大而单调提升，并作为性能上界。从图6中可以发现，随着K从64增加到128，各种方法的性能都有所提升。这可以通过在固定带宽情况下，增加载波数量K，会使得载波间隔Δf变小，从而增强了相邻载波之间的相干性来解释。然而，缩短Δf会使得系统对频偏更加敏感，导致Single-FFT的性能在K达到128之后开始下降。对于具有ICI抑制效果的其他方法，则可以延缓这种下降趋势，P-FFT、FFFT、PS-FFT、PC-FFT的性能分别是在载波数K达到256、512、512、1024之后开始明显下降。也就是说这些方法相比Single-FFT 增大了系统可以使用的最大载波数，从而提高了系统的传输速率和带宽效率。

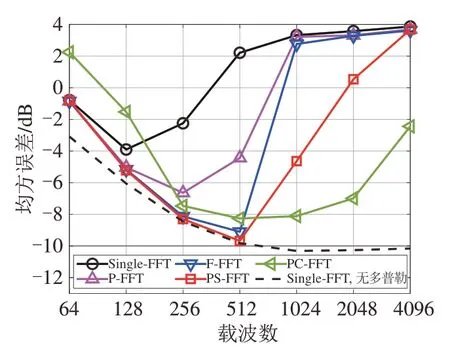
图6 不同载波数下5种方法的MSE性能（基于仿真水声信道）Fig.6 MSE performance of five methods under different carrier numbers （based on the simulation UWA channel）

另一方面，对于PC-FFT，在利用特征值分解法求解权重向量wk时，是认为每个子区间内所有载波上的wk都相等。当K较小时（例如64、128和256），由于每个OFDM 符号上的导频总数KP较少，因此没有划分子区间。显然，在宽度等于系统带宽B=12 kHz的长区间里，认为各载波上的wk都相等不够合理，此时使得特征值分解法求得的wk不够准确。另外考虑到补偿频率向量fe是按逐符号的方式求解，即KP越大，求解精度越高，因此当K较小时，KP较小导致fe的求解精度也较低。

综上，当K较小时，由于分区间宽度较长和KP较小，使得wk和fe的求解精度都较低，从而PC-FFT在低载波数下的性能不如PS-FFT 等方法。而随着K的增大，分区间数增大，单个子区间的宽度减小，以及KP增大，使得wk和fe的求解精度增大，PC-FFT的检测性能最终在K达到1024 时，开始超过PSFFT。因此，对于PC-FFT 要尽可能使用较大的载波数，这点与差分相干检测为保证相邻载波间的强相干性，要尽量使用较大的载波数不谋而合。此外，当K=4096时，P-FFT、F-FFT 和PS-FFT 的MSE 都接近4 dB，BER 也都接近50%的乱猜概率，即无法工作。而此时PC-FFT 仍能保持-2.44 dB 的MSE 性能，即相比PS-FFT 等方法，PC-FFT 进一步拓宽了系统最大可使用的载波数范围。

接下来，本小节测试了上述5 种方法在不同信噪比下的符号检测MSE 和BER 性能，结果如图7 所示，其中，信噪比是在0～30 dB 的范围内变化，多普勒因子和载波数分别设置为α=3.5×10-4和K=1024。从图7 中可以看出，当α达到3.5×10-4时，P-FFT 和F-FFT 的MSE 和BER 和Single-FFT 十分接近，且BER 接近50%的乱猜概率，也就是说P-FFT和F-FFT 由于抑制能力有限，此时都几乎完全无法正常工作，因此这里重点关注PS-FFT 和PC-FFT 的性能。由于这两种方法在α=3.5×10-4时，都具有较强的ICI 抑制能力，二者都具有较好的MSE 和BER 性能。具体而言，当信噪比在10～30 dB 的范围内变化时，相比PS-FFT，PC-FFT 将MSE 降低了55.08%～67.64%，将BER降低了91.94%～98.85%。

图7 不同信噪比下5种方法的MSE和BER性能（基于仿真水声信道）Fig.7 MSE and BER performance of five methods under different SNRs （based on the simulation UWA channel）

然后，本小节也测试了5 种方法的运行时间对比，结果如图8 所示，其中多普勒因子、载波数和信噪比分别设置为α=3.5×10-4、K=1024 和SNR=30 dB。从图8 中可以看出，F-FFT 的运行时间略高于P-FFT 的运行时间，说明从频域补偿多普勒频偏的做法的复杂度要略高于从时域分段减小时变性的做法。结合图5～图7 的性能测试结果，F-FFT 虽然相比P-FFT 略微增加了复杂度，但能带来更好的性能。同样地，对于PS-FFT 方法，由于兼具了时域分段和频域补偿的做法，其复杂度比P-FFT 和FFFT都要高，但相比二者也能带来不小的性能提升。此外，对于PC-FFT 方法，虽然由于需要同时求解补偿频率和权重，导致复杂度明显高于只需求解权重的PS-FFT等方法，但能在大多普勒因子性能显著优于PS-FFT 等方法。具体而言，虽然P-FFT、F-FFT 和PS-FFT 等方法复杂度低，但它们利用基于梯度下降的方法求解权重，且在每个载波处只迭代一次，对于初始点和步长的设置十分敏感，鲁棒性较低。PC-FFT采用基于特征值分解的算法，以非自适应的方式求解权重，且在迭代求解补偿频率前，以假设检验的方式获得一个较为合适的频率迭代起始点，鲁棒性较高，即降低了对初始参数配置的敏感度。此外，F-FFT 和PS-FFT 是在预设的频率上做补偿，而PC-FFT 通过在动态优化得到的频率上做补偿，可有效提升系统自主跟踪动态多普勒频偏的能力。

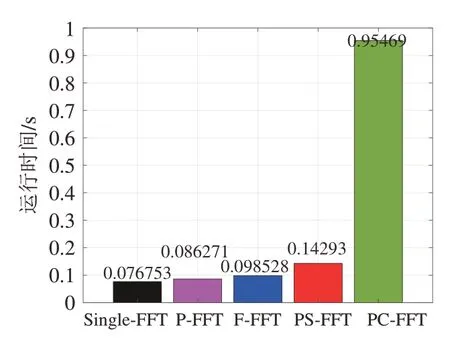
图8 5种方法的运行时间对比Fig.8 Running time comparison of five methods

进一步，图9定量展示了算法1中各主要步骤的耗时占比。具体而言，统计了第9 步（Step 9）、第10步（Step 10）、第13 步（Step 13）和其它步骤（Other Steps）的运行时间占算法1 总运行时间的比重。其中，第9步是对接收信号r(t)和信号t⋅r(t)分别进行PC-FFT解调，第10步是利用特征值分解法求解权重向量，第13步是计算梯度。从图中可看出，第9步导致了绝大部分耗时，达到了90%以上，第10 步和第13 步的耗时分别约为5.5%和3.9%，其余步骤的总耗时不到0.2%。第9步耗时大的原因是执行傅里叶变换，虽然使用了加速算法FFT，但计算开销仍不小。而且，在迭代求解权重和补偿频率的过程中，需执行步骤9多次。经测试统计，算法1平均在每个OFDM符号上要迭代约18次，即步骤9要被执行18次，单次的运行时间虽短，但18次迭代将显著增加耗时，致使PC-FFT方法的运行时间超过PS-FFT的。

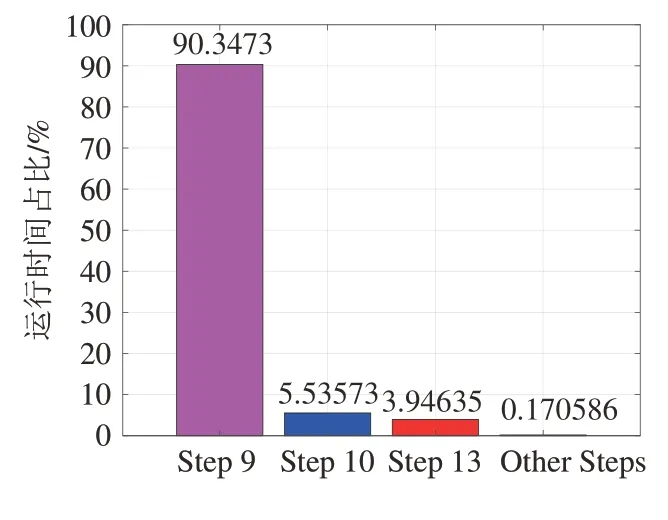
图9 算法1中各步骤运行时间占比Fig.9 Proportion of running time for steps in Algorithm 1

最后，本小节也测试了不同分段数A下PC-FFT方法的符号检测MSE 性能，结果如图10 所示，其中，信噪比是在0～30 dB 的范围内变化，多普勒因子和载波数分别设置为α=3.5×10-4和K=1024，测试了分段数A分别取2、3 和4 时的性能。从图10 中可以看出，分段数A=3 时的MSE 性能整体上要优于A=2 时的性能。而当分段数A增大到4 时，MSE性能在SNR 较低时相比A=3 时甚至要略微更差，说明增大分段数A，MSE 性能不会单调地改善，当超过某一值，性能反而会恶化，其可能原因是参数过拟合。具体而言，当分段数A增大时，权重向量wk中的元素增多，即在权重和补偿频率的联合优化问题中需要求解的参数量增多，更容易发生参数失配，即过拟合的问题，从而使得系统性能下降，在文献［8］和［16］的测试结果中也发生了类似的现象。此外，增大分段数也会提升系统的复杂度。因此，在实际应用时，需要折中考虑性能和复杂度来确定分段数。

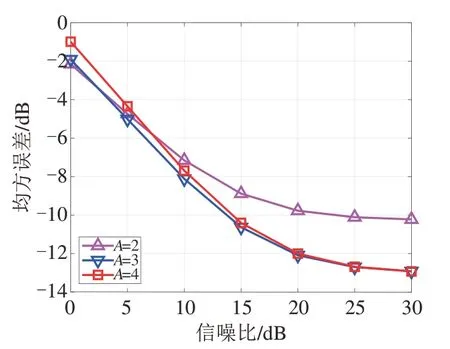
图10 不同分段数下PC-FFT方法的MSE性能Fig.10 MSE performance of PC-FFT under different segment numbers

4.2 基于实测水声信道的实验

Watermark 是一个基于实测信道数据的水声通信仿真平台，其中包含了采集自多个真实海洋环境中的信道数据［17］。基于这一平台，实验者能够在MATLAB 等仿真软件上能模拟信号经过实际水声信道的过程。截至到目前，Watermark包含了5组测试信道的数据，分别为NOF1［18］、NCS1［18］、BCH1［19］、KAU1［20］和KAU2［20］。其中，NOF1、NCS1和BCH1 分别采集自挪威奥斯陆峡湾、挪威大陆架和法国布雷斯特海港、KAU1 和KAU2 则采集自美国夏威夷州考艾岛。在这5 组信道中，NOF1 和NCS1 为单入单出（Single-Input Single-Output，SISO）信道，其他三种为单入多出（Single-Input Multiple-Output，SIMO）信道。由于本文研究工作目前考虑的是具有单个接收单元的差分OFDM 系统，因此，本小节利用NOF1 和NCS1 这2 种单入单出信道，构建了仿真系统，来开展对PC-FFT 等方法的性能测试。本小节将先介绍仿真系统的具体参数配置，然后展示用此参数配置获得的测试结果，并予以分析。

4.2.1 仿真参数设置

表4 总结了仿真系统的主要OFDM 参数配置，其中各项参数基本与表1 相同，主要区别在于表4是将中心载波频率和带宽分别设置为fc=14 kHz和B=8 kHz，即信号频带范围为10～18 kHz，用以适配NOF1 和NCS1 信道的频率范围。表5 总结了4 种ICI 抑制方法的参数配置，其中，考虑到NCS1 信道条件较为恶劣，因此在本小节的仿真实验中，4种方法在每帧OFDM 数据中都是使用了NP=1024 个导频。对于PC-FFT，在基于特征值分解求解权重向量时，本小节中是将分区间数设置为S=4。

表4 基于实测水声信道的仿真实验OFDM系统参数配置Tab.4 Parameter settings of the OFDM system in the simulation based on the actual-measured UWA channel

表5 基于实测水声信道的仿真实验ICI抑制方法参数配置Tab.5 Parameter settings of the ICI mitigation methods in the simulation based on the actual-measured UWA channel

此外，根据Watermark 平台提供的资料，NOF1和NCS1 信道的平均多普勒速度分别为0.0625 m/s和0.1580 m/s，折算的归一化多普勒因子分别为4.167×10-5和1.053×10-4。由于这两个多普勒因子数值较小，为了观测在不同多普勒因子下的性能，因此在设计的仿真程序中的通过重采样来添加多普勒效应对信号的影响时，没有按原本的多普勒因子去重采样，而是按自定义的多普勒因子重采样。由于在本小节的仿真测试中，信道的最大多普勒因子为αmax=10-3，对应的中心载波上的频偏为fd，max=αmaxfc=14 Hz，因此，在本小节中是将PSFFT的基准偏移频率fe设置为fe=2fd，max=28 Hz。对于PC-FFT方法，在联合求解前的假设检验阶段，则是先从-28 Hz到28 Hz范围内，以7 Hz为间隔取出9个频率分别对每帧的第1个OFDM符号进行预解调。

4.2.2 仿真结果及分析

图11和图12分别展示了上述5种方法在NOF1信道和NCS1信道中的符号检测MSE 随多普勒因子α的变化曲线，其中信噪比是固定为SNR=10 dB，多普勒因子α是在10-4～10-3的范围内变化。首先可以看出，5种方法在NCS1信道中测试得到MSE结果基本都要高于在NOF1信道中测试结果，这与Watermark平台所介绍的NCS1信道比NOF1信道更为恶劣的事实保持一致。此外，从图11 和图12 也可以看出，无论是NOF1 信道还是NCS1 信道，5 种方法的MSE随α增长而增加的速度从高到低依次为Single-FFT、P-FFT、F-FFT、PS-FFT 和PC-FFT，即PC-FFT 由于显示地估计了频偏，对α增大的敏感度最低。

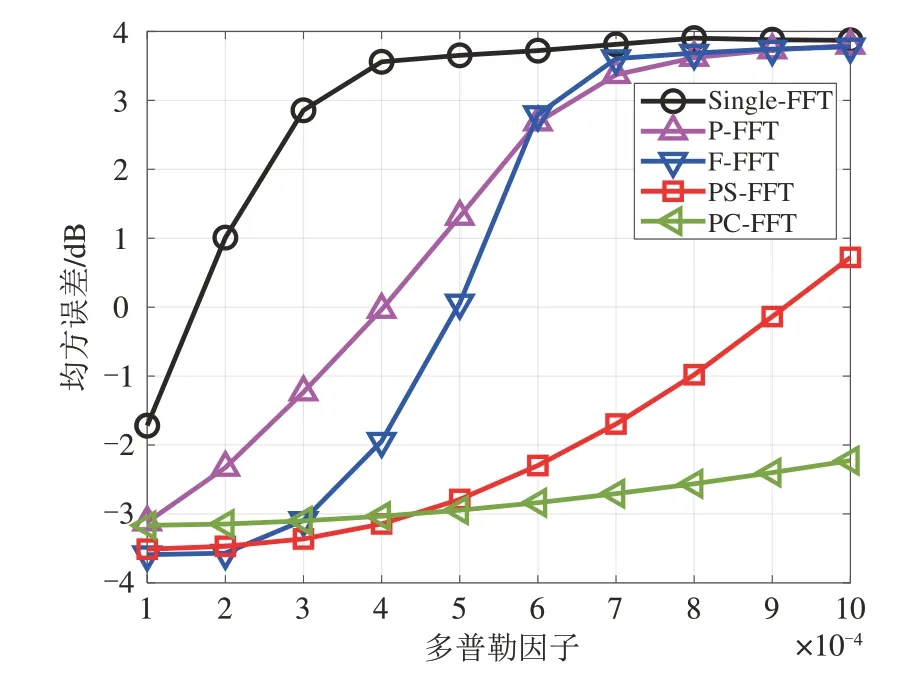
图11 不同多普勒因子下5种方法的MSE性能（基于NOF1信道）Fig.11 MSE performance of five methods under different Doppler factors （based on the NOF1 channel）

图12 不同多普勒因子下5种方法的MSE性能（基于NCS1信道）Fig.12 MSE performance of five methods under different Doppler factors （based on the NCS1 channel）

在图11 和图12 中，虽然当α较小时，PC-FFT 的MSE 高于PS-FFT、F-FFT 和P-FFT 的MSE，但差距较小。随着α的增大，PC-FFT 的性能开始逐渐赶上和超过PS-FFT等方法。当α=10-3时，对于NOF1信道和NCS1 信道，P-FFT 和F-FFT 的MSE 都十分接近Single-FFT的MSE，其对应的BER也非常接近50%的乱猜概率，即P-FFT和F-FFT此时在两种信道中都几乎完全无法工作。而两种时频协同的方法：PS-FFT和PC-FFT，此时都能维持较好的性能。进一步地，当α=10-3时，在NOF1 信道和NCS1 信道中，相比PSFFT，PC-FFT可分别将MSE降低49.29%和15.56%。

图13 和图14 则分别展示了上述5 种方法在NOF1 信道和NCS1 信道中的符号检测MSE 和BER性能随信噪比的变化曲线，其中多普勒因子固定为α=10-3，SNR 是设置在0～30 dB 的范围内变化。首先可以看出，对于P-FFT 和F-FFT，无论是在NOF1信道还是NCS1 信道中，其MSE 和BER 曲线和Single-FFT 的曲线一样都几乎不随SNR 增加而下降，进一步说明了当α=10-3时，两种单域方法在NOF1 和NCS1 信道中都几乎完全无法工作，因此这里重点关注PC-FFT和PS-FFT方法。

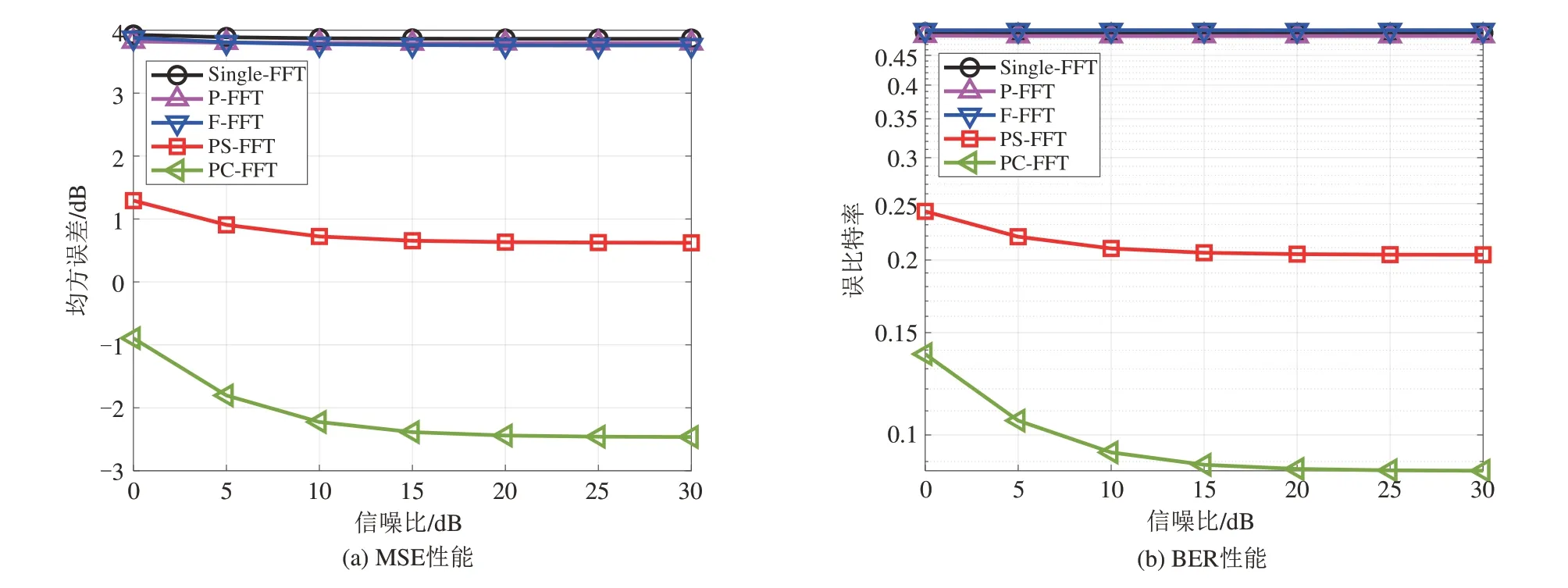
图13 不同信噪比下5种方法的MSE和BER性能（基于NOF1信道）Fig.13 MSE and BER performance of five methods under different SNRs （based on the NOF1 channel）

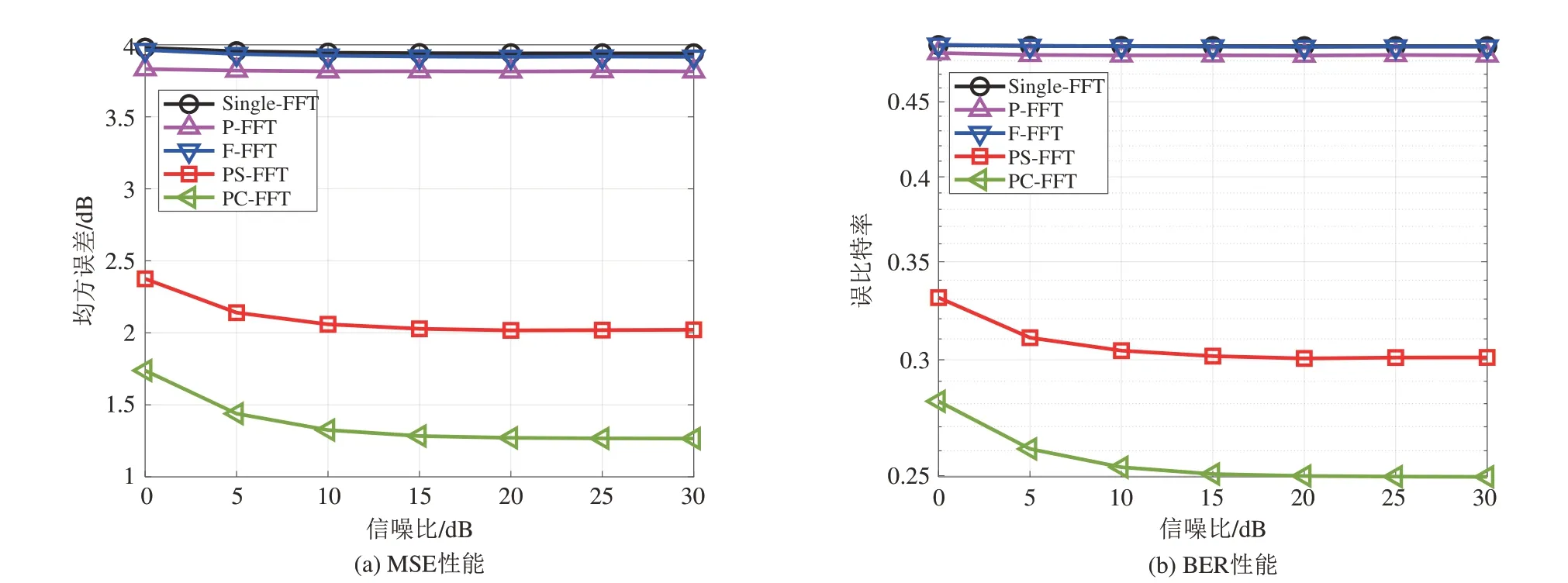
图14 不同信噪比下5种方法的MSE和BER性能（基于NCS1信道）Fig.14 MSE and BER performance of five methods under different SNRs （based on the NCS1 channel）

从图13 和图14 中可以看出，PC-FFT 和PS-FFT由于在α=10-3时都具有较好的ICI抑制能力，二者的MSE 和BER 都在SNR 较小时，能随着SNR 增大而降低。但当SNR达到15 dB之后，2种方法的MSE和BER 几乎没有再随SNR 增加而下降。造成这种现象的可能原因是在实际环境中采集信道数据时，不可避免地存在噪声，即NOF1和NCS1信道数据中本身就存在噪声，且对应的SNR 大小约为15 dB。因此，在仿真测试时，如果设置的SNR 在15 dB 以下，其对应的噪声幅度要大于NOF1和NCS1本身所包含的噪声的幅度，即仿真添加的噪声占主导性因素，因此，此时增大SNR，能较为有效地改善系统的性能。而当设置的SNR 大于15 dB 后，其对应的噪声幅度小于NOF1 和NCS1 本身所包含的噪声的幅度，即仿真添加的噪声不占主导性因素，因此，此时再增大SNR，对于系统性能的改善较小。

此外，在图13 和图14 中，对于两种时频协同的ICI 抑制方法，PC-FFT 方法的曲线要低于PS-FFT，即验证了PC-FFT 在大多普勒因子下ICI 抑制能力的优越性。具体而言，对于NOF1 信道和NCS1 信道，当SNR 在0～30 dB 的范围内变化时，相比PSFFT 方法，PC-FFT 方法可分别将MSE 降低39.56%～50.86%和13.63%～15.97%，将BER 降低43.20%～57.50%和15.04%～17.12%。

5 结论

本文提出了一种称之为PC-FFT 的ICI 抑制方法，其协同时域和频域抑制ICI，以在大多普勒频偏场景下提升差分OFDM 系统的检测性能。具体而言，首先，在时域上将OFDM符号持续时间划分为几个非重叠的短区间，以减小信号时变性；然后，在频域上对每一段短信号分别在一个待优化的频点上做补偿；最后，线性加权各段补偿短信号的傅里叶变换。为了求解权重和补偿频率，建立了以二者为变量，以最小化检测均方误差为目标的优化问题。鉴于该优化问题的高度非凸性，为降低求解复杂度，设计了一种基于坐标轮换下降的求解算法。进一步地，在该求解算法中，权重和补偿频率分别使用特征值分解和梯度下降法求解，且二者依次交替求解直至收敛。基于仿真和实测水声信道的测试结果均验证了在大多普勒频偏场景下，PC-FFT的性能显著优于现有的P-FFT、F-FFT和PS-FFT等方法。