基于改进联合概率数据关联的AUV定位算法

李鑫滨 马迎港 闫 磊 韩 松

（1.燕山大学，河北省工业计算机控制工程重点实验室，河北秦皇岛 066004；2.东北大学秦皇岛分校计算机与通信工程学院，河北秦皇岛 066004）

1 引言

海洋中蕴含着大量的矿产资源、海洋生物资源等，海洋探索与开发成为国际各领域炙手可热的研究方向［1］，水下自主机器人因为其在执行水下任务时的灵活性以及其经济性，已广泛应用于许多的海洋应用之中，如水下图像数据采集［2］、水下军事检测［3］、海洋突发环境应急［4］等，但水下自主航行器（Autonomous Underwater Vehicle，AUV）在这些领域中的应用必须依靠准确的定位才能有效。水下无线传感器网络（Underwater Wireless Sensor Networks，UWSN）利用声学信号作为通信介质，使用基于距离的定位方法，为AUV的水下环境的定位通信提供了一个良好的平台。在基于距离的定位方法之中，基于到达时间（Time of Arrival，TOA）由于有更好的鲁棒性［5］，在UWSN中已经得到了广泛使用。一阶线性化的拓展卡尔曼滤波（Extended Kalman Filter，EKF）通过使用TOA 的方法获取信标节点和AUV 之间的距离测量并实现AUV 的定位，由于其简单、计算复杂度低等优点［6］，是目前估计AUV 位置最常用的方法。

传统的EKF 算法的应用是在已知过程噪声和测量噪声协方差的前提下进行的，然而在实际的水下环境中由于外部干扰和环境变化等因素［7］，导致准确的噪声协方差矩阵很难确定，而且可能是时变的，使用错误或不准确的噪声协方差矩阵会导致大量的累积估计误差，甚至滤波发散。针对这个问题，文献［8］提出了自适应调节先验误差协方差矩阵的强跟踪滤波器，文献［9］提出了用于未知测量噪声协方差矩阵的自适应Sage-Husa 滤波算法，实时估计和修正噪声统计量来自适应跟踪过程中的噪声变化，然而当同时估计过程噪声协方差矩阵和测量噪声协方差矩阵时，估计值与真实值之间存在着一个常值误差，即不可能同时估计出真实的过程噪声协方差矩阵和测量噪声协方差矩阵。在文献［10］中提出一种迭代拓展卡尔曼滤波AEKF，使用期望最大化算法（Expectation-Maximum，EM）同时自适应估计预测误差协方差矩阵和测量噪声协方差矩阵，解决了上面的问题，期望最大化算法［11］是一种通过迭代进行极大似然估计的优化算法，在对模型的参数进行迭代当中其似然函数值一般是递增的，但EM 算法在优化过程中的重要前提是需要合理的模型参数迭代初值，如果所设置的迭代参数初值与现实所对应的参数差距很大，则算法很有可能迭代出错误的模型参数，陷入到局部最优解中［12］。所以，该算法在应对水下突发意外环境中的定位时的鲁棒性会大大下降。

值得注意的是，水下节点通常部署在无人值守的开放声环境中，这使外来的恶意节点可通过伪装成为合法的邻居信标节点，然后在信标节点与AUV的距离测量数据传输中，恶意节点在拦截消息后通过延迟响应［13］，可以很容易的在传输数据包中的时间戳和在测距数据中注入恶意噪声，使得接收节点得到错误的距离测量，危及无线传感器网络中待定位的AUV位置准确估计。因此，在水下定位系统中进行恶意噪声检测以保证整个网络的可用性［14］是十分有必要的。目前，研究人员已经提出了一些恶意噪声检测的方法，文献［15］中基于估计水下声学信号的平均传播速度来判断和删除恶意信标节点信息。文献［16］基于Cayley-Menger 行列式和l1最小化解码算法的几何约束，构造了一个距离测量的离群值检测模型，通过丢弃异常值、只使用可靠的数据来估计未知节点的位置。文献［17］使用基于密度的空间聚类来识别恶意噪声，但基于密度的识别方法存在参数设置敏感的问题，如果恶意噪声的攻击的频率比较高时，产生的测量点对应的密度就会比较分散，此时针对识别恶意噪声所设置阈值就会比较困难。此外，在筛选出未受恶意噪声污染的测量点后，还存在需要对这些测量点进行数据融合的问题，传统的联合概率数据关联（Joint Probabilistic Data Association，JPDA）算法是处理一批测量点并对目标进行定位更新的有效算法［18］，通过对落入其以预测点为中心的关联门的测量点进行数据关联进行定位更新。在文献［19］中对传统JPDA 进行了改进，通过在预测点的周围生成服从高斯分布的虚拟测量点以提高定位精度。但是数据关联在当前时刻的后验位置估计要使用所有的历史时刻的测量点，随着时刻增加，贝叶斯估计中的历史测量占比也会随之增加，而当前获取的测量所占的比重太小，当系统存在模型误差和噪声误差时，会减小当前时刻获取的测量点对位置估计的作用。

在本文中，首先我们在EKF 的更新过程中进行测量噪声误差协方差迭代，然后基于计算噪声误差协方差矩阵的相似度的方法，检测信标节点与AUV节点之间的距离测量是否受到了恶意攻击的污染，接着，为了丰富输入测量点的样本以提高定位的精度，我们在没有受到恶意噪声污染的测量点以及预测点的周围生成服从高斯分布的虚拟测量点，最后，对于没有受到恶意噪声污染的测量点、生成的虚拟粒子进行数据关联和更新，输出当前时刻最终的后验位置估计和后验误差协方差，并且会作为下一时刻EKF 的先验估计的输入，由于消除了恶意噪声的影响，在提高定位精度的同时，在下一时刻恶意噪声检测阶段能得到正确的参数迭代值，从而保证了MJPDA算法正常运作。仿真结果表明，该方法能有效地检测出异常值，并且与现有工作相比，所提出的定位方法具有较高的精度。

2 网络架构与问题描述

2.1 网络架构

为了进一步说明所提出的水下多AUV 定位算法，我们考虑了一种包含三种不同类型节点的水声无线传感器网络架构，如图1所示。

图1 水声无线传感器网络场景图Fig.1 Illustration of the UWSN

1）水面浮标节点：水面浮标节点安装有全球定位系统（Global Positioning System，GPS），通过与卫星之间的电磁波通信获取自身的准确实时位置。水面浮标节点的作用是为水下信标节点提供自定位服务。

2）水下信标节点：水下已固定好的各个信标节点通过与水面浮标节点的直接通信，并获得其自身位置。信标节点向待定位的水下多AUV 节点发送水声信号，AUV在接收到信号后基于TOA方法获取到各个信标节点与AUV 之间准确的距离测量。然而，外来的恶意节点可以捕获水声网络中的水下信标节点并伪造其信号特征，通过向传输的距离测量数据包中注入恶意噪声，使得AUV接收到来自被恶意攻击后的错误测距信息，从而影响AUV目标节点的定位精度。

3）待定位的多AUV节点：在水下待定位的多个AUV 移动目标节点配备了边缘计算系统，在得到当前时刻来自各个信标节点的测距信息后，使用本文提出的改进联合概率数据关联算法对受到污染的距离测量进行筛选，并对其自身进行位置估计。

2.2 AUV运动系统模型

在实际的水下AUV定位中，由于通过AUV配备的压力传感器可以获得精确的深度，所以AUV的深度获取和平面的位置估计是相互独立的。此外，由于复杂的水下环境，AUV 的垂直速度存在显著的测量误差，这可能会大大降低深度估计的运动模型的准确性。因此，我们在有精确的深度测量时，不必建立状态变量中含有深度信息的AUV运动状态模型。所以在本文中，待定位的AUV节点的深度并没有被包含在状态变量之中，三维定位问题被简化为二维定位问题。状态变量随着时刻k变化的模型为：

其中，(xAUV，n(k)，yAUV，n(k))，n=1，…，N为N个待定位AUV 在时刻k的位置坐标，Δt为单位采样时间，分别为第n个AUV 上配备的DVL 提供的其右舷和前向速度，是第n个AUV 使用罗盘测量的航向，wk-1，n=[wx，k-1，n，wy，k-1，n]T表示服从高斯分布的过程噪声，即wk-1，n～N(0，Qk-1，n)，其中Qk-1，n是过程噪声协方差，T为转置运算。

本文使用基于TOA 方法获取M个信标节点与N个AUV 目标节点之间的距离测量。然而，水声通信环境中影响TOA 测量模型的因素十分复杂，若不考虑水声环境因素（如时变多普勒、多径效应、分层效应等）直接使用TOA 测距模型，一定会影响所得到测距信息的准确性。最近关于水声定位的一些文献［20-22］中对于在水声环境中使用TOA 的方法获取准确测距信息已经得到了充分的研究，为了简化，我们在以往研究的基础上假设了在水下环境中使用TOA 方法来获取准确的距离信息的合理性，以此更加贴近真实的水下环境。

在第k个时刻，定义第m个信标节点与n个AUV之间的相对距离测量为：

其中，AUV 在k时刻的位置定义为(xAUV，n(k)，yAUV，n(k)，hAUV，n(k))，n=1，…，N，hAUV，n(k)和hBN，m(k)分别为通过压力传感器准确测量得到AUV 和信标节点的深度。

由于AUV 和信标节点的深度是由压力传感器精确测量得到的，所以我们利用TOA 的相对距离以及深度信息进行反算可以得到AUV 和信标节点之间的水平距离，因此这里的三维距离测量lm，n(k)可以被转换为二维距离测量dm，n(k)

考虑TOA方法的距离测量噪声，在第k个时刻第m个信标节点n个AUV之间的二维测量方程可以被表示为：

其中，M个信标节点的位置坐标(xBN，m(k)，yBN，m(k))，m=1，…，M假设通过浮标节点提供的自定位服务获取为已知，并且通过水声通信广播给所有的水下AUV 目标节点；δm，n，k为未遭受恶意噪声攻击或者存在恶意噪声攻击下的距离测量噪声。在没有遭受攻击的情况下，该信标节点的测量噪声δm，n，k=ρ被建模为高斯白噪声ρ～N(0，Rm，n，k)，其中Rm，n，k为测量噪声协方差；在本文中我们考虑了与文献［15］中类似的恶意噪声攻击模型，存在恶意噪声攻击的情况下，测量噪声δm，n，k=ρ+γc，其中为恶意噪声，μγ和分别为恶意噪声的均值和协方差。

注：三维距离测量lm，n(k)被转换为二维距离测量dm，n(k)的过程中距离测量噪声的分布会偏差为长尾的彩色测量噪声，从而导致测量噪声并不满足高斯分布。然而，在本文中并不需要建立上述测量噪声的精确模型，通过自适应地估计预测协方差矩阵和测量噪声协方差矩阵，缓解了具有不准确的测量噪声模型的负面影响；并且在本文中使用基于矩阵相似度的恶意噪声识别机制，将测量噪声的模型简化为高斯白噪声不会影响到恶意噪声的检测部分。所以我们在三维的水下AUV 定位问题转换为二维定位问题的过程中，将测量噪声模型在本文中简化为一个高斯白噪声是合理的设置。

由式（1）、（3），将建立的AUV 运动系统模型表述为一般形式：

其中，状态转移矩阵F=I2，I2为二维单位矩阵，过程噪声wn，k-1与测量噪声δm，n，k互不相关，即，其中E[⋅]=0为期望运算。

3 改进联合概率数据关联算法

在上一节中，我们基于TOA 的方法获取了假设位置已知的M个信标节点与待定位的N个AUV目标节点之间的距离测量，对于其中一个AUV目标节点，在时刻k可以从M个信标获取对于该AUV的距离信息。在本节中我们对该AUV 目标节点进行EKF 的先验估计，得到该AUV 目标节点的先验位置估计（也就是AUV 的预测点）和先验误差协方差Pk|k-1，然而，在开放的水声环境中，外来的恶意节点很容易在所得到的M个距离测量中注入恶意噪声，从而导致最终定位精度的下降。所以我们在AUV的初步定位之前通过恶意噪声检测以排除其影响。

首先，利用期望最大化算法对M个距离测量对应的先验协方差Pm，k|k-1和测量噪声误差协方差Rm，k进行在线迭代估计；接着，我们基于计算测量噪声误差协方差矩阵相似度来识别距离测量是否受到恶意噪声污染，并且丢弃受到恶意噪声污染的距离测量。对于保留的P个未被恶意噪声污染的距离测量每三个一组进行分组，利用最小二乘法对AUV目标节点完成对AUV的初步定位，由此我们在当前时刻可以获得个AUV 目标节点位置的最小二乘解，n=1，…，Ni（由初步定位得到的Ni个测量点）；为了丰富测量点的样本以提高定位的精度，与传统的JPDA 算法相比，我们在没有受到恶意噪声污染的测量点以及预测点的周围生成服从高斯分布的虚拟测量点；最后，对于没有受到恶意噪声污染的测量点以及生成的虚拟粒子进行数据关联和更新，完成当前时刻AUV的精确定位。输出当前时刻最终的后验位置估计和后验误差协方差，并且会作为下一时刻EKF 的先验估计的输入。由于输出的后验位置估计和后验误差协方差是使用通过恶意噪声检测阶段的测量计算得到的，所以能有效保证MJPDA算法在恶意噪声环境下的鲁棒性。如图2为MJPDA的流程图。

图2 改进的联合概率数据关联算法流程图Fig.2 Flowchart of MJPDA

3.1 EKF先验估计

由于在式（5）中的测量方程中的h(xn，k，xBN，m，n，yBN，m，n)是非线性的，所以我们使用EKF 的先验估计对进行AUV 当前位置的预测。利用k-1时刻通过MJPDA 得到的AUV 目标节点后验位置估计和后验误差协方差Pk-1|k-1，得到k时刻AUV 的先验状态估计和先验误差协方差Pk|k-1。

同时我们得到k时刻的AUV 位置的预测点

3.2 恶意噪声污染检测

在本节中我们设计了一种基于噪声协方差矩阵相似度的恶意噪声检测机制，首先，针对水声环境中由于外部干扰产生的时变噪声协方差，将在线EM算法应用于EKF中，基于历史k个时刻信标节点与AUV 之间的测距信息dm，1：k，m=1，…M，来在线估计先验误差协方差Pm，k|k-1和测量噪声协方差Rm，k，其中表示信标节点m由时刻1 到时刻k与AUV 之间的距离测量；在得到迭代N次的测量噪声协方差后，我们分别计算每个信标对应测量噪声协方差矩阵与所设置的初代测量噪声协方差矩阵Rk的相似性，用来判断k时刻信标节点m使用TOA 方法获取的距离测量是否受到了恶意噪声的污染。

使用EM 算法迭代参数Φm，k≜{Pm，k|k-1，Rm，k}，主要分为两步，即E步（Expectation）和M步（Maximization）迭代求解距离测量关于模型参数Φm，k的对数似然函数logp(xk，dm，1：k，Φm，k)的极大似然，从而得到参数Φm，k的估计值。

E 步：根据贝叶斯公式，距离测量dm，1：k和AUV在时刻k迭代估计的参数Φk完全数据联合概率分布可以被定义为：

所以，用公式（9）～（11）可以计算出完全数据对数似然函数logpΦm，k(xk，dm，1：k)。

在l+1代，通过利用l代的后验状态估计和后验协方差得到更精确的非线性测距测量方程的泰勒线性化近似h(xk，xBN，m，yBN，m)。

计算l+1迭代的卡尔曼增益：

计算l+1代的后验状态估计：

计算l+1代的后验协方差：

迭代l次的参数下的后验密度函数可以被近似高斯分布，其均值和方差分别为l+1迭代中的后验估计和后验协方差。

M步：

在M 步中，极大化在E 步中得到的Q(Φm，k，)，然后求解等式获取l+1 代的先验误差协方差、测量噪声协方差；并且在通过N次迭代后得到了每一个距离测量对应的测量噪声协方差矩阵。

当UWSN 中部分信标节点受到恶意噪声的影响时，相应迭代出的测量噪声误差协方差将产生异常值。借助图像识别中的相似度原理，我们分别计算每个信标对应测量噪声协方差矩阵与所设置的初代测量噪声协方差矩阵Rk的相似性，定义和Rk的矩阵相似度为：

其中，相似度的计算结果αm∈[-1，1]，αm的值越接近1，说明矩阵的相似度越高，越接近0 则说明两个矩阵的相似度越低。经过恶意噪声的污染迭代出的噪声协方差矩阵与设置的初代噪声协方差矩阵具有明显差异，所以他们经计算得到的相似性最低。

通过计算噪声误差协方差的相似度，我们将受到恶意噪声污染的距离测量丢弃，保留未遭受恶意噪声污染的距离测量。在识别检测之前，在时刻k对于一个AUV 目标节点我们有M个测距信息m=1，…M，在噪声识别检测以后保留有P个未遭受恶意噪声污染的距离测量(P≤M)。这样，在进行初步定位估计之前，我们通过恶意噪声污染检测消除了其对AUV定位效果的影响。

3.3 分组和初步定位

上一节中得到了P个检测为没有受到恶意噪声污染的距离测量，为了获取到尽可能多的测量点以提高定位精度，我们直接将P个距离测量按照排列组合进行分组，然后利用最小二乘法来获取AUV初步定位，n=1，…，Ni，其中为P个测距信息按照三个一组被分为不同组的组数。

对于其中的一组，根据距离测量值可建立以下方程：

其中，dn，1(k)、dn，2(k)、dn，3(k)为第n组内信标节点的距离测量，(xBN，1：3，yBN，1：3)为分组内对应信标节点的位置坐标，为组内信标节点对应经迭代得到的噪声误差协方差矩阵。为了使用最小二乘法得到AUV 的初步定位，式（19）被表达为线性矩阵形式Y=AX：

为了求解AUV的初步定位，定义如下残差向量方程：

使AUV的位置坐标残差的平方和最小，对残差向量方程求导并令其为零：

得到AUV 位置的最小二乘解，完成AUV 的初步定位：

3.4 产生虚拟测量

考虑到信标节点的部署成本，在同一片海域当中不适宜部署过多的信标节点。同时，在有恶意噪声的环境下，MJPDA 算法丢弃了受恶意噪声污染的测量点。针对测量样本的稀疏性，与传统的JPDA算法相比，MJPDA 为了提高定位精度，在通过AUV初步定位得到的良好测量点与预测点的附近产生了服从高斯分布的虚拟测量。

为了产生虚拟测量的范围，我们首先确定未遭受恶意噪声影响的信标节点n当前时刻对应的新息协方差：

并且由新息协方差确定测量点对应的关联门的面积，在本文中关联门是指以良好测量点与预测点为中心，用来限制产生虚拟测量的范围。这个范围的大小主要由当前时刻该测量对应的新息协方差和关联门概率确定。落入到关联门内的测量被称为候选测量点。通常，关联门被认为是一个“gsigma”椭圆面［23］，关联门的面积为：

其中，α为MN 坐标向量的维数，cα为α维关联门的单位面积。本文中为二维定位场景，所以α=2，c2=π。同时，γ服从具有两个自由度的卡方分布。然后，如果检测到正确的输入测量点的概率PG可以表示为：。

为了简化虚拟测量的生成过程，我们将椭圆关联门简化为正方形，边长定义为l：

其中，(Nx(k)，Ny(k))为产生的所有虚拟测量的位置坐标，N1(l，l/2)和N2(l，l/2)是均值为l、方差为l/2 的高斯分布。因此，最终输入到数据关联和更新阶段中的测量点主要包含：经过AUV初步定位得到的测量点、AUV 位置的预测点、以及在他们周围产生的虚拟测量点，为了接下来推导方便，将它们统一定义为zm(k)。

3.5 数据关联和更新

我们在上一节当中得到了要输入到数据关联算法的测量，则这测量关于先验估计的新息为：

在初步定位得到的量测点中，如果存在受到所选择的信标和AUV 的相对位置的影响导致定位精度极差的测量点，首先，我们会对其进行筛选，将检验统计量Tm(k)计算为：

为了验证输入测量，定义了以下假设：

其中，H0，m如果为真，则输入的测量值将被添加到有效测量值集合中，否则将被丢弃。注意，有效测量值为，i=1，2，…，Nv，其中Nv是有效测量集合中的有效测量点个数。所以在经过以上的筛选之后，AUV 和信标节点的相对位置较差导致所构建的定位方程秩亏对最终的精确定位结果影响不大。

然后，在我们的推导当中关联矩阵可以被表示为：

其中，关联矩阵的第一列都为1 表示测量值并非来自于AUV 目标节点。因为所有的输入测量值都可以通过杂波或虚警来产生，关联矩阵的第二列表示输入的测量值是否与AUV相关联，如果相关联则对应的元素为1，如果不关联则对应的元素为0。对关联矩阵进行拆分，我们得到互联矩阵Ωi(k)，每一个互联矩阵表示不同的互联事件。

计算每一个互联事件的概率，也就是测量点为目标准确定位的概率βm，与文献［24］的随机权重不同，本文所提算法的权重是确定性的。与随机权重相比，确定性权重能够使基于良好测量点的估计状态的贡献最大化，使恶意测量的估计状态的贡献最小化。

测量值并非来自于AUV目标节点的概率β0：

最后，根据计算得到的互联概率的值，我们得到后验状态估计和后验误差协方差。

卡尔曼增益矩阵：

后验状态估计为：

后验误差协方差计算为：

在得到当前时刻最终的后验状态估计和后验协方差，我们将它们放入到MJPDA的下一时刻的先验计算中使用，可以有效提高算法在恶意噪声影响下的鲁棒性。

4 仿真分析

在本节中，对于本文所提出的MJPDA 算法在MATLAB R2021a上进行了仿真模拟，对二维场景下两个同时做匀速运动的目标场景进行了测试，以验证所提定位算法的有效性。首先通过仿真实例证明在相同参数下所提定位算法优于所对比的算法；然后通过进行不同参数的变化对均方根误差（Root Mean Square Error，RMSE）的影响，证明所提算法对于处理恶意噪声提升定位性能是有意义的。

在图3 所示的二维定位场景中，600 m×600 m的区域内随机部署了6 个信标节点来定位2个AUV目标节点。蓝色实线和红色实线分别代表两AUV利用改进的联合概率数据关联算法在恶意噪声影响下所估计得到的运动轨迹，蓝色虚线和红色虚线则分别表示两AUV 沿着固定的轨迹进行匀速直线运动，在轨迹附近的蓝色点与红色点表示为提高定位精度而产生的测量点。MJPDA 的门概率被设置为PG=0.99，检测概率被设置为PD=0.95。不考虑信标节点的功耗，假设所有的信标节点总可以与AUV 节点进行有效的通信。每个仿真实验结果通过500 次的蒙特卡洛模拟运行得到，所对比的算法JPDA 和AEKF［9］的默认参数设置与MJPDA 一致，在表1中给出了仿真中所使用的参数。

表1 仿真参数Tab.1 Simulation parameters

图3 定位两个AUV的位置估计Fig.3 Simulation results for two AUVs tracking

定义在每一次蒙特卡洛模拟中的平均定位误差（Average Localization Error，ALE）：

根据ALE 我们可以得到三种算法平均误差的累积分布函数（Cumulative Distribution Function，CDF），CDF是指在某个精度门限下的定位次数在总定位次数中所占比例，图4 的仿真结果可以看出，MJPDA 的百分之八十的定位误差都小于3.3 m，相比之下，JPDA 算法和AEKF 百分之八十的定位误差分别小于5.1 m 和7.9 m。图4 的仿真结果表明，总体来说，定位系统处于存在较大恶意噪声和累积估计误差的影响情况下，MJPDA 的定位精度优于现有算法JPDA和AEKF。

图4 经验分布函数与定位误差Fig.4 CDF and Localization Error

接下来，在图5 至图7 的仿真结果中我们将显示在不同参数的变化下（恶意噪声出现的概率、恶意噪声的均值、信标节点数量）详细讨论MJPDA、JPDA 和AEKF 的三种算法的比较，利用RMSE 进行算法性能的评价。

图5 恶意噪声出现概率对均方误差的影响Fig.5 RMSE and different probability of Malicious Noise

其中，K表示一次蒙特卡洛模拟中的总采样时长，Tn表示蒙特卡洛运行的次数，且K=130，Tn=500。

在通常的水声对抗情形下，噪声干扰往往是饱和的，所以我们利用恶意噪声出现概率来体现对抗环境中恶意噪声干扰的饱和性。在图5 中，横轴为其他参数不变的情况下恶意噪声出现的概率从0.1到1，纵轴为蒙特卡洛的定位误差。随着恶意噪声对一个信标节点与AUV 之间的距离测量产生影响概率的增加，对比的两种算法的定位误差都在增加，其中AEKF的定位误差增加的较为显著，这是因为较大的恶意噪声破坏了测量噪声误差协方差的迭代环境，从而影响了定位效果。当恶意噪声出现的概率比较小的时候，MJPDA 和JPDA 算法的定位精度比较接近。随着恶意噪声出现的概率增加时，由于所提出的MJPDA 提前筛选出了受污染的距离测量，所以仍然可以保持较好的定位精度，仿真结果表明，MJPDA 在场景中经常出现恶意噪声时可以具有更好的定位精度。

在图6中，保持了其他参数的不变的同时，恶意噪声的均值在每一次蒙特卡洛中从3 m 增加到10 m，随着恶意噪声误差均值的增加，AEKF的RMSE呈线性增加，JPDA 的RMSE 增加相对缓慢，MJPDA的定位误差几乎没有增长。当恶意噪声误差的标准差从3 增加到10 时，仿真结果表明，JPDA 通过关联门丢弃具有较大残差的离群值来实现其鲁棒性，但如果有多个离群值连续出现，其定位效果将会降低。MJPDA 受恶意噪声误差扰动的影响较小，具有较强的鲁棒性，这是因为MJPDA在恶意噪声的检测环节中，丢弃了所有受到恶意噪声污染的距离测量。

图6 恶意噪声的均值对均方误差的影响Fig.6 RMSE and the mean value of Malicious Noise

为显示信标节点数量对于锚节点定位精度的影响，我们使信标节点的数量从4 个增加到10 个，如图7 所示。虽然增加了信标节点的数量，但恶意噪声对AEKF 的均方根误差的影响仍然较大。同时，随着信标节点数量的增加，JPDA 和MJPDA 算法的定位误差都在减小。在信标节点数量较少时，由于MJPDA 在预测点和未受到恶意噪声污染的测量点附近都生成了虚拟测量，比JPDA 算法拥有更丰富的样本值，因此JPDA算法的效果不如MJPDA好。仿真结果表明，随着信标节点数量的增加，两种算法的定位精度趋于一致，但在信标节点数量较少时，MJPDA 拥有更好的定位精度，即MJPDA 在水下物联网的节点部署稀疏时拥有更好的定位表现。

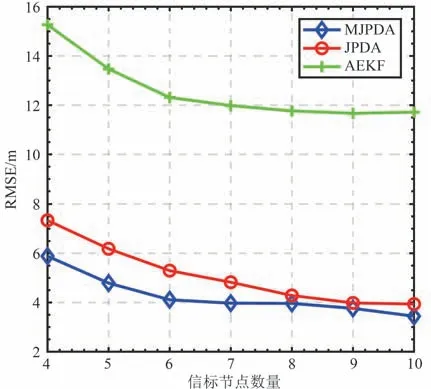
图7 信标节点数量对RMSE的影响Fig.7 RMSE and the number of beacon nodes

5 结论

本文对存在恶意噪声攻击情况下的AUV 定位进行了研究，提出了一种改进的联合概率数据关联定位方法（MJPDA），考虑了水下环境中存在恶意噪声攻击情况下的AUV定位追踪，设计了一种基于误差协方差迭代算法的恶意噪声攻击检测方法，通过基于计算当前时刻迭代出的误差协方差相似度的方式检测出受到恶意噪声污染的测量，并且完成AUV 的初步定位。与传统的JPDA 相比，在预测点和未受到恶意噪声污染的测量点附近都生成了虚拟测量点，对这些测量点进行数据关联处理与更新，完成对AUV目标节点的精确定位。仿真结果证明，所提出的MJPDA定位算法能够保证存在恶意噪声攻击情况的网络环境下具有良好的性能，对研究如何安全定位水下机器人具有一定的意义。