基于群稀疏整体最小二乘的多节点探测阵高精度被动定位方法

张云潇 杨成竹 徐立军

（北京理工大学信息与电子学院，北京 100081）

1 引言

水下目标被动探测是水下声学领域研究的一个热点问题。在传统的单节点探测中，有三种广泛使用的被动定位方法：三子阵法，匹配场处理（Matched Field Processing，MFP），以及目标运动分析（Target Motion Analysis，TMA）。三子阵法将单节点线阵划分为三个子阵，利用各子阵对于目标的方位估计，从各子阵参考点出发，绘出三条定位线，最终判断目标位于三条定位线的交汇处。这种方法操作简单，但定位精度受阵列尺寸、时延估计精度、目标距离、信号强度等因素影响，目前主要应用于近距离定位。匹配场处理［1］结合了水下声传播理论和信号处理技术，根据真实的海洋环境建模得到拷贝场向量，并运用线性或自适应处理器对实测声场进行匹配运算，实现对目标的距离和深度估计。但真实的环境模型与建模总是存在偏差，当环境失配时，匹配场处理方法的性能会急剧下降。目标运动分析［2］是一种通过收集一段时间内的观测数据，例如方位和频率，来确定目标位置的方法。在传统的单节点观测中，与其他信息相比，测量的方位信息更加准确。但在单组阵列下，纯方位TMA 要求观测平台机动，这限制了其实际应用。频率-方位TMA虽然不要求观测平台机动，但对于信噪比有较高要求，难以适应复杂的海洋环境［3］。此外，由于人类社会经济活动加剧，海洋环境噪声逐年增强，再加上舰船防震减噪技术的发展，过去几十年重要目标的辐射噪声平均每年降低约1 dB，单节点探测阵的输入信噪比极低，其作用距离和精度都越来越无法满足实际需求。

针对单节点探测在低信噪比环境下性能下降严重的问题，多节点探测提供了新的解决方案［4］。根据定位步骤，可将多节点定位技术分为两类，即传统两步法和直接定位法。传统两步法在第一步中求解定位参数，例如信号到达时间差（Time Difference Of Arrival，TDOA）［5］、信号到达角方向（Direction of Arrival，DoA）［6］、接收信号强度（Received Signal Strength，RSS）［7］等。依据定位参数，绘制定位线，在第二步中利用定位参数与辐射源位置之间的关系建立方程求解。目前常用的数据关联算法有最小距离法，最大似然法及拉格朗日松弛法等［8］。但在多源条件下，辨别交点的有效性，进行正确的数据关联较为困难，这极大限制了两步法的实际应用。

与传统两步法不同，直接定位法通过对探测区域划分网格，构建信号源位置的代价函数，采用穷尽搜索等方式实现一步定位。以色列学者Weiss 提出直接定位法（Direct Position Determination，DPD），其利用多个固定节点，综合考虑到达角（Angel Of Arrival，AOA）及TDOA 构建最小二乘模型，实现了对单个窄带信号源的定位［9］。随后，基于多重信号分类（MUltiple SIgnal Classification，MUSIC）的DPD算法被提出，用以解决多源定位问题［10］。此外，基于最小方差无失真响应（Minimum Variance Distortionless Response，MVDR）的DPD 算法［11］也可用于解决多源定位问题，并且克服了DPD-MUSIC算法需要预知信号源数量的缺点。相较于DPD-MUSIC，DPD-MVDR 的定位精度并没有显著提升，当存在多个辐射源时，算法要解决的问题是渐进有偏的，其定位精度难以达到理论的克拉美罗下限（Cramer-Rao Lower Bound，CRLB）［12］。

基于目标信号在时空频等展开域所表现出的特性，进行目标位置建模，是设计优化定位算法的关键所在。其中，稀疏重构类方法仅需要较少的快拍数就能实现多目标DoA 估计，因此受到学术界的广泛关注。如D.Malioutov 等人的L1-SVD（Singular Value Decomposition）方法，基于目标在空域所展现出的天然稀疏性，进行目标位置（方位）的L1稀疏优化建模，随后利用成熟的凸优化技术来实现目标位置信息的获取［13］。稀疏贝叶斯（Sparse Bayesian Learning，SBL）从最大化后验概率的角度出发，关注稀疏信号的统计特性，且能确保算法的解为全局收敛解的近似［14］。更进一步，Yang等人利用泰勒展开的方式减小所构建的字典与真实字典的差距，给出了稀疏贝叶斯算法的离格形式［15］。然而，稀疏重构类方法虽然在单节点定位任务中已经取得了巨大成功，但较少应用在多节点直接定位任务中。如何在多节点有效作用范围内，有效利用目标所展示出的稀疏特性，是本文所要解决的关键问题。

综上所述，针对当前水下多节点定位算法多目标分辨困难，定位精度不足的问题，本文基于目标在空间中的稀疏特性，通过将目标所处区域网格化，构建基于群稀疏的多节点目标被动定位模型，并采用群稀疏优化技术实现直接定位。为解决网格失配引起的定位精度缺失问题，本文对联合阵列流形矩阵一阶泰勒展开，构建离格定位模型，采用群稀疏整体最小二乘算法，实现对目标位置的高精度估计。仿真实验表明，对于长宽均为1 km 的探测区域，在4组节点情况下，所提模型和算法均是正确有效的，能对多目标位置进行正确解算。大网格间距下，相较于稀疏模型，离格模型能够进一步降低10 m 左右的定位误差。不同网格间距下的对比试验表明，本文所提出的离格定位模型对于网格间距有较强的鲁棒性。相较于传统两步法及经典的直接定位法，单源及多源情况下，信噪比不低于-5 dB时，本文所提出的基于群稀疏整体最小二乘的离格直接定位算法具有更高的定位精度。

2 多节点探测阵接收信号模型

本文拟采用四组均匀线阵实现对探测区域内的多目标进行精确定位，相关的建模方法也适用于其他数量节点。下面将展开介绍提出的多节点探测阵接收信号模型。

考虑K个窄带信号源sk(t)，k=1，…，K，阵列接收待测源信号的方位角记作θi，k，多节点的阵列观测模型如下：

其中yi(t)=[yi，1(t)，…，yi，M(t)]T表示阵列接收信号，ei(t)=[ei，1(t)，…，ei，M(t)]T表示观测噪声，m=1，…，M分别代表第i组阵列的第m个阵元在t时刻的观测信号及噪声。a(θi，k)=[a1(θi，k)，…，aM(θi，k)]T，am(θi，k)表达式如下：

式中，d代表阵元间距，c代表声速。

多阵列协同探测示意图如图1所示。黑色实线所围成网格区域即为探测区域；四个蓝点代表四组均匀线阵，其连线围成了一个相较于探测区域更小的绿色实线网格区域，称其为聚焦区域；红点代表信源k，信源k与各阵列所成的角度均已在图1 中标明。当阵列处在网格线上时，阵列所在行或列所对应的阵列流形完全相同，此时所形成的阵列流形矩阵相关性极高，不利于高精度定位，所以我们在阵列流形矩阵中删除各阵列起始点所在的行和列，这导致探测的盲区域出现，即图1 中的灰色区域。将第i组阵列的起始阵元坐标(xi，yi)作为该节点远距离定位时的参考坐标，第k个信源的坐标为(xk，yk)，可以得出方位角的表达式如下：

将公式（3）代入公式（2），用位置变量(xk，yk)代替角度变量θi，k，即得到关于目标位置变量的接收信号模型如下：

3 基于稀疏重构的直接定位算法

本节将在建立的接收信号模型的基础上，综合利用各节点的观测信息，从目标稀疏性的角度出发，构建代价函数，给出基于稀疏重构的直接定位算法。在3.1节中，假设目标均在划分的网格点上，给出基于L1-SVD 的直接定位算法。在3.2节中，探讨如何缩小离格误差，通过对联合阵列流形矩阵一阶泰勒展开，实现对失配网格的修正，给出基于群稀疏整体最小二乘的离格直接定位算法。

3.1 基于L1-SVD的直接定位算法

记Yi=[yi(1)，…，yi(T)]，S=[s(1)，…，s(T)]，Ei=[ei(1)，…，ei(T)]。观测模型被重写如下：

其中阵列流形矩阵Ai的大小为M*N，M为阵元数，N=P*Q为网格点数，P为总列数，Q为总行数。信号矩阵S的大小为N*T。假设在聚焦区域内存在K个信号源，K≪N，显然信号矩阵S是稀疏的［16］。建立如下的优化问题：

记Y=[Y1，Y2，Y3，Y4]T，A=[A1，A2，A3，A4]T，式（6）可进一步写作如下形式：

该问题为一个典型的LASSO（Least Absolute Shrinkage and Selection Operator）问题，可以采用迭代软阈值算法（Iterative Soft Thresholding Algorithm，ISTA）求解，求解过程如下：

1）初始化梯度下降步长α，正则化参数λ。

2）对于式（7）中的可导部分||Y-AS||F，对S作梯度下降，实现对S的半步更新。半步更新公式如下：

3）软阈值收缩，完成余下的半步更新。

4）如果本次更新结果满足

则终止迭代。否则，返回第2）步，继续迭代。

Matlab 中cvx 工具箱也可用于求解此类优化问题。为使用cvx 求解，需对公式（7）作如下等价转换：

其中，ε为超参数，可通过多次测试选取。

此外，为了降低算法的计算量和对噪声的敏感性，采用SVD 对数据进行降维。单独的对每个观测矩阵Yi进行降维将会造成信息量的损失。因此，对联合观测矩阵Y=[Y1，Y2，Y3，Y4]T作SVD 分解，来确保没有损失四组观测数据之间的关联信息。令Y=USVH，V=[V1V2]，其中V1为V的前K列，V2为V的余下T-K列，并据此将观测数据分为信号子空间和噪声子空间。从而，有YSV=YV1∈CM×K，足以代表所有的观测信息［17］。

记YiSV=YiV1，SSV=SV1，EiSV=EiV1。各个节点观测数据的SVD分解格式如下：

采用公式（13）的SVD 分解格式能够提升程序的运行速度且不会使算法的精确度下降，仿真验证将在4.2节中给出。算法的整体流程如图2所示。

图2 基于L1-SVD的直接定位算法Fig.2 Direct position determination based on L1-SVD

3.2 基于群稀疏整体最小二乘的离格直接定位算法

在上一节中，我们给出了基于L1-SVD 的直接定位算法，但on-grid 类方法的缺点在于必须用网格对探测区域进行划分，网格划分的细致与否将直接影响定位的结果。理想情况下，信号源全部位于划定的网格点上，此时定位误差最小。但实际上，信号源的位置与网格点总是有所偏差。因此，当网格划得过粗时，模型存在较大的误差。但网格划分过细，又会导致联合阵列流形矩阵列相关性增大，增加定位的难度。此外，更细的网格将导致计算量的显著提升，最终使得模型难以应用于实际［18］。针对这一问题，我们提出了基于群稀疏整体最小二乘的离格直接定位算法，下面将详细叙述。

图3 位置偏移量Fig.3 The position offset

采用一阶泰勒展开构建新的导向向量形式：

因此，观测模型可以被写为：

基于公式（16）的离格模型，建立如下的优化问题：

其中，β=[βx，βy]，Y=[Y1，Y2，Y3，Y4]T，Φ=[Φ1，Φ2，Φ3，Φ4]T。这种基于整体最小二乘思想的稀疏重构方法被称为稀疏整体最小二乘（Sparse Total Leastsquares，STLS）［19］，在求解时，我们运用了群稀疏的思想，所以称本节的方法为G-STLS。公式（17）可等价转化为如下问题：

公式（18）所给出的优化问题是非凸的，一种简便的求解方法是将这个非凸问题拆分为两个凸优化问题求解：

通过拆分，将计算分为了两个模块，这两个模块均可以直接采用cvx 工具箱进行处理，交替迭代这两个模块，公式（17）的稀疏整体最小二乘问题得到解决。

此外，偏移量βx和βy的维度取决于总网格数，其维度均为N×1。事实上，采用如此完备的βN×1是没有必要的，经过L1-SVD 已经得到了信源最接近的网格点位置，仅对这些位置对应的βK×1进行更新，能够极大地减小计算联合阵列流形矩阵时的计算量。详细的论证过程如下：

式（17）、式（18）的计算量分别为(2N+1)MN，(2K+1)MK。节点数为4，K＜＜N，单步中所减少的计算量为4M(2N+2K+1)(N-K) ≈8MN2。显然，格点数N越大，减少的计算量越多。算法的整体流程如图4所示。

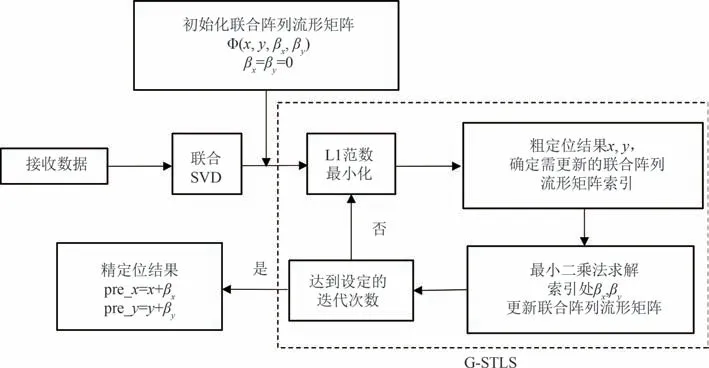
图4 基于G-STLS的离格直接定位算法Fig.4 Off-grid direct position determination based on G-STLS

4 基于稀疏重构的直接定位算法仿真实验

在本节中，我们将给出基于L1-SVD 的直接定位算法和基于G-STLS 的离格直接定位算法在不同网格间距、不同信噪比下的性能表现，重点在于展示引入离格模型后算法的性能提升情况。在仿真实验中，考虑一块海深固定的大小为1 km*1 km的二维平面探测区域，假定四组接收阵列的起始阵元坐标分别为（250 m，250 m），（750 m，250 m），（250 m，750 m）以及（750 m，750 m）。阵列所围成的区域大小为500 m*500 m。每组均匀线阵具有8个阵元，阵元间距设置为半波长，当有多个信源时，取波长均值的一半。对信源的位置作如下要求：1.为了满足远场条件，设定信源不会出现在以阵列起始点为圆心、50 m 为半径的范围内。2.信源不会出现在图1 所示的盲区域内。各节点噪声相互独立，且均为高斯白噪声。考虑两个频率为800 Hz 及900 Hz 的单音信号，采样频率10 kHz，快拍数20。为了避免G-STLS算法的运行时间过长，设定其交替迭代次数为15次。采用平均绝对误差（MAE）来衡量算法的定位精度，其被定义如下：

其中R代表蒙特卡洛实验数目，K代表单次测试中的信源数目。分别代表单次实验中信源的真实位置和算法预测位置。

4.1 L1-SVD及G-STLS的定位结果

本次实验设定SNR=0 dB，网格间距dx=dy=50 m。设置两信源坐标分别为（482 m，490 m）和（618 m，610 m）。算法的定位结果如图5所示。

图5 L1-SVD及G-STLS定位结果Fig.5 The localization result of L1-SVD and G-STLS

实验结果表明，L1-SVD 及G-STLS 算法均能估计出两信源的位置。此外，因为G-STLS具有离格估计的能力，所以G-STLS 的定位性能必然优于L1-SVD，这在图5中表现为更小的定位模糊区域。

4.2 算法运行时间优化

与DoA 估计问题相比，多节点联合定位问题更为复杂，需要处理更多的节点数以及更多的网格点数，这将导致计算量的显著提升。在第3 节关于算法原理的讨论中，我们提出了联合SVD、偏移量维度缩减的方法用于优化算法，减小算法的计算量和运行时间。在本节中，我们将展示采用这两种优化方式前后，算法的定位精度及运行时间的对比实验结果。

4.2.1 联合SVD

本节将通过实验验证SVD 对直接定位算法的影响。以基于L1-SVD 的直接定位算法为例。设定SNR=0 dB，网格间距dx=dy=25 m。设置两信源坐标分别为（482 m，490 m）和（618 m，610 m）。算法的定位结果如图6及表1所示。

表1 L1和L1-SVD的平均绝对误差及运行时间Tab.1 MAEs and Runtime of L1 and L1-SVD

图6 L1及L1-SVD定位结果Fig.6 The localization result of L1 and L1-SVD

由实验结果可知，SVD 在加快算法运行速度的同时，提炼了信号的主要特征，使得稀疏类算法能够恢复出更加稀疏准确的解。

4.2.2 偏移量维度缩减

算法的收敛速度是评价迭代算法的重要指标［20］。本节将给出单次实验下，使用βN×1和βK×1时G-STLS算法的收敛情况。设定SNR=10 dB，两个信源的位置分别为（482 m，490 m）和（618 m，610 m）。网格间距dx=dy=50 m。实验结果如图7 和表2所示。

表2 βN×1和βK×1的平均绝对误差及运行时间Tab.2 MAEs and Runtime of βN×1 and βK×1

图7 采用βN×1和βK×1时G-STLS收敛情况Fig.7 The G-STLS convergence of βN×1 and βK×1

由实验结果可知，当采用βK×1时，G-STLS 在30 次迭代后就已经完全收敛。而采用βN×1时，GSTLS在80次迭代时仍未能完全收敛。由表2可知，采用βK×1能够节省大量的运行时间，为算法应用于实际提供了可能。

4.3 G-STLS与L1-SVD的对比实验

本次仿真实验设定SNR=10 dB，0 dB，-5 dB，网格间距dx=dy=50 m，40 m，25 m，20 m。聚焦区域内存在两个信源，两信源的x轴间距及y轴间距均为100 m。每个信噪比及网格间距下进行400 次蒙特卡洛实验。实验结果如图8所示。

实验结果表明，G-STLS 在不同网格间距、不同信噪比下均拥有更低的预测误差。当采用50 m 的网格间距时，相较于L1-SVD，G-STLS 能够降低10 m左右的定位误差。值得注意的是，在中高信噪比下，采用大网格间距并不会带来显著的误差提升，这意味着本文提出的G-STLS 算法对离格位置的逼近效果良好，在网格间距的选取上，具有较强的鲁棒性。

5 与现有算法的对比实验

在本节中，我们选取多种经典直接定位算法作为主要对比试验算法。在5.1 节单源对比试验中，给出了DPD、DPD-MUSIC、DPD-MVDR、AOA-SBL，与L1-SVD、G-STLS 算法在不同信噪比下的定位性能比较。在5.2 节多源对比试验中，给出了DPDMUSIC、DPD-MVDR，与L1-SVD、G-STLS 在不同信噪比下的定位性能比较。

5.1 单源情况下的对比实验

对于传统两步法，我们采用SBL 计算信号源到达各节点的方位角，绘制定位线，构建超定方程组，并采用最小二乘法解算定位线交点，求得源位置。为方便表示，将该方法记作AOA-SBL。现有的经典直接定位算法DPD、DPD-MUSIC、DPD-MVDR 均可实现对单信号源的定位。在本节中，我们将基于稀疏重构的直接定位算法L1-SVD 及G-STLS 与上述直接定位算法在不同信噪比下进行对比。本次仿真实验固定网格间距dx=dy=25 m，设定SNR=-10 dB，-5 dB，0 dB，5 dB，10 dB。考虑频率为800 Hz的单音信号，采样频率10 kHz，快拍数20。每个信噪比下进行100 次蒙特卡洛实验。实验结果如图9所示。

图9 单源对比实验Fig.9 Single-source comparison experiments

实验结果表明，当信噪比不低于-5 dB 时，4 种on-grid 算法DPD、DPD-MUSIC、DPD-MVDR、L1-SVD以及传统两步法AOA-SBL的定位精度基本相当，本文提出的离格算法G-STLS具有最高的定位精度，在SNR=-5 dB 的情况下定位误差在5 m 左右。当信噪比进一步降低至-10 dB，此时3 种经典的直接定位算法DPD、DPD-MUSIC、DPD-MVDR 仍具有较高的稳定性，定位误差小幅度提高，传统两步法AOASBL 彻底失真，L1-SVD 定位误差大幅攀升，导致GSTLS定位误差也随之攀升。

5.2 多源情况下的对比实验

经典直接定位算法中的DPD-MUSIC、DPDMVDR 可实现对多源信号的定位。在本节中，我们展开对比实验，对比基于稀疏重构的直接定位算法L1-SVD、G-STLS与DPD-MUSIC、DPD-MVDR 算法在不同信噪比下的定位性能。本次实验固定网格间距dx=dy=25 m，设定SNR=0 dB，3 dB，5 dB，7 dB，10 dB。考虑两频率为800 Hz、900 Hz 的单音信号，采样频率设置为10 kHz，快拍数设置为20。每个信噪比下进行100 次蒙特卡洛实验。实验结果如图10所示。

实验结果表明，现有的直接定位算法DPDMUSIC、DPD-MVDR 虽然能解决多源定位问题，但其定位精度存在很大的提升空间。针对网格失配问题，本文在G-STLS算法中给出的离格定位模型能够减小因信号源不在网格点上而导致的离格误差，使定位精度大幅提升。

6 结论

针对当前水下多节点定位算法存在的多目标分辨困难，定位精度不足等问题，本文利用目标信号在空间中的稀疏特性，提出了一种基于群稀疏的多节点目标被动定位模型，并采用群稀疏优化技术求解模型参数以实现多目标的精确直接定位。为解决网格失配引起的定位精度缺失问题，本文使用一阶泰勒展开对联合阵列流形矩阵进行近似，构建离格定位模型，采用群稀疏整体最小二乘算法，实现对目标位置的高精度估计。仿真实验表明，所提模型和算法均是正确有效的，能对多目标位置进行精确解算。不同网格间距下的对比试验表明，本文所提出的离格定位模型对于网格间距有较强的鲁棒性。相较于传统两步法及经典的直接定位法，本文所提出的基于群稀疏整体最小二乘的离格直接定位算法针对单源及多源定位问题，在信噪比不低于-5 dB的情况下具有更高的定位精度。