入轨精度对降交点地方时的影响分析

李伟建,刘旭光,刘兴威,邓海琴

酒泉卫星发射中心,酒泉 732750

0 引言

入轨精度既是运载火箭的重要性能参数,也是衡量发射飞行任务成败的重要指标,而对太阳同步轨道而言,其一个重要特征是在这条轨道上运行的卫星从相同的方向经过同一纬度时的当地时间相同,也即降交点地方时相同。对降交点地方时的研究主要集中在3个方面:1)分析降交点地方时的变化规律及计算方法,如文献[1]基于在轨遥测数据分析了轨道倾角和降交点地方时的运动变化规律,文献[2-3]研究了地球非球形摄动影响下的降交点地方时漂移估计方法;2)研究降交点地方时的控制策略,文献[4]提出通过轨道偏置设计、轨道高度和轨道倾角保持控制等方法将降交点地方时漂移控制在允许范围内,文献[5]提出了一种主动控制策略,而文献[6]提出了一种被动控制策略,文献[7-8]研究了变轨前后降交点地方时不变的轨道转移问题;3)分析降交点地方时变化对其它因素的影响,文献[9]研究了降交点地方时漂移对光学相机成像质量的影响,文献[10]通过调整降交点地方时来减小对目标区域的重访间隔。卫星发射入轨后,如果不变轨,轨道性能就基本确定,发射入轨时的精度就成了影响卫星轨道性能的首要因素,而目前少有学者从入轨精度的角度来研究这一问题。本文从工程的角度出发探讨了太阳同步轨道设计和降交点地方时的计算问题,详细分析了入轨精度对太阳同步轨道降交点地方时的影响,通过研究发现,入轨时的误差是导致降交点地方时漂移的主要因素,入轨精度三要素对降交点地方时的漂移有不同的影响,这对火箭发射、入轨精度设计、入轨精度分析评定、漂移反向控制等具有重要意义。

1 太阳同步轨道设计

根据载荷成像能力,先确定其轨道高度,这里假设轨道高度h已知。若太阳同步轨道为圆轨道,则需要设计确定的轨道要素主要为轨道倾角和升交点赤经。

1.1 轨道倾角计算

仅考虑J2的长期摄动时,太阳同步圆轨道的半长轴a和轨道倾角i之间必须满足以下关系:

(1)

式(1)中:Re为地球赤道平均半径,a=Re+h。

1.2 升交点赤经计算

如图1所示,假设目标区域中心O的经纬度为λm和φm,A为O点处经线与赤道的交点,B为太阳同步轨道的降交点,轨道倾角为i,则图中O,A和B三点在地心天球上形成了一个球面直角三角形,根据球面直角三角形的计算公式可计算出Δλ和u,如式(2)[11]:

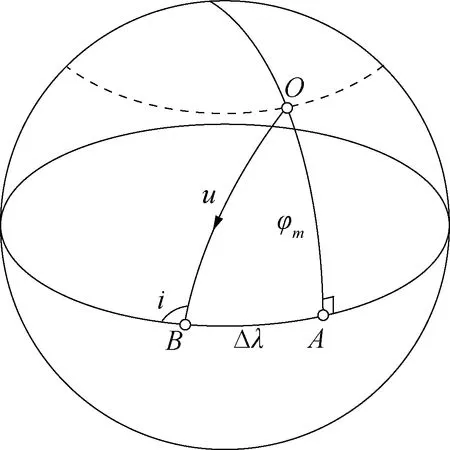
图1 目标区域中心与降交点之间的球面三角形示意图

(2)

假设要求卫星对目标区域中心进行成像时的当地地方时为Td,则卫星当圈通过降交点时的当地地方时TDe为:

(3)

式(3)中:T为成像卫星的轨道周期,由式(4)计算:

(4)

式(4)中:a为轨道半长轴,μ为地心引力常数。从式(3)可知,过目标区域的地方时与降交点地方时有确定的关系,选取二者之一即可,工程中一般以降交点地方时作为发射轨道参数的要求。与TDe对应的升交点地方时TAs为:

TAs=TDe+12 h

(5)

由目标区域中心O点处的经度λm可计算出升交点经度λAs为:

(6)

式(6)中:ωe为地球自转角速度。则升交点赤经Ω和升交点经度λAs之间的关系为:

Ω=λAs+θ(t)

(7)

式(7)中:θ(t)为在升交点时刻t时(UTC时间)的格林尼治时角,由式(8)计算。

(8)

式(8)中:JD(t)为计算时刻t对应的儒略日。

而升交点时刻t时的UTC时间可由地方时TAs换算获得,计算式为:

(9)

因此,只要给定Td或者TDe,就能根据上述计算过程求得升交点赤经Ω。

2 卫星轨道降交点地方时计算方法

(10)

2.1 轨道外推算法

对卫星受力考虑的精细化程度不同,产生了多种轨道动力学模型,也就有了多种卫星轨道外推算法,如J2摄动、J4摄动、Simplified General Perturbations(SGP4)、High-Precision Orbit Propagator(HPOP)等。一个高精度的外推算法也是卫星轨道设计的前提,这里给出考虑J4摄动的具体外推模型。设卫星的位置矢量为r=(x,y,z),r=|r|。对于近地轨道,地球摄动的主要因素是地球的扁状。四阶带谐项引力位摄动函数可以写为[12]:

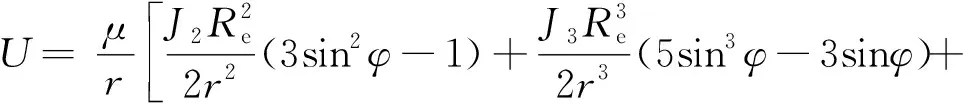
(11)

其中:μ为地心引力常数,Re为地球赤道平均半径,φ为被吸引点在地心坐标系的地心纬度,J2,J3,J4为摄动模型系数,J2=-0.001082616,J3=2.53881×10-6,J4=1.65597×10-6。计算赤道惯性坐标系下位函数的梯度,可以得到卫星在赤道惯性直角坐标系下的摄动加速度分量,将其叠加到二体模型,获得考虑J4引力摄动的轨道递推模型为:

(12)

2.2 卫星轨道位置LLA计算

由轨道递推公式(12)求得任意时刻卫星的位置[xyz]T,由下式将其转换到地心空间直角坐标系:

(13)

式(13)中:αG是θ(t)的角度值。再由地心空间直角坐标系转换为大地坐标系,通常采用式(14)。

(14)

当采用式(14)计算大地纬度时,需要采用迭代方法,每次迭代按照式(15)进行。

(15)

式(15)中:a和e分别为地球参考椭球的半长轴和偏心率,常选取CGCS2000椭球参数。当|Bi-Bi-1|小于指定的精度时,迭代结束。一般在保证h的计算精度为0.001 m和B的计算精度为0.00001″的情况下,仅需迭代4次左右。

联立式(12)～(14)可以求得任意t时刻卫星轨道位置的经纬高(L,B,h),则过降交点的条件为:

B=0&&B′>0

(16)

3 多因素正交试验设计

为了揭示入轨精度对卫星过目标区域地方时的影响情况,应用正交试验设计方法开展仿真试验计算,确定的试验因素为半长轴偏差、轨道倾角偏差、偏心率偏差,采用三水平正交表L16(43),各因素及其水平具体数值如表1所示。

表1 入轨精度各要素正交设计表

采用Matlab-STK联合仿真方法开展正交试验,具体的正交试验实施流程如图2所示。

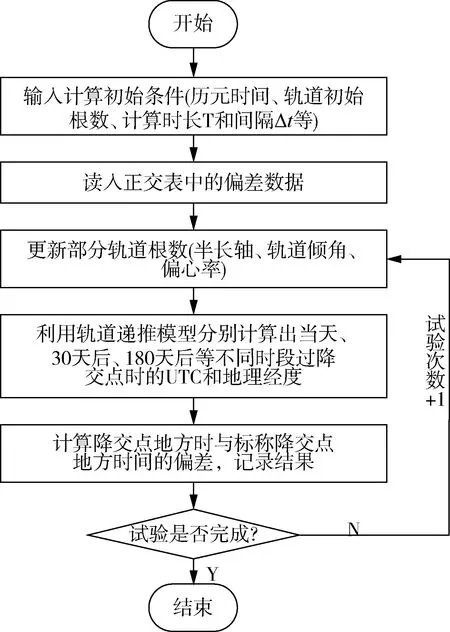
图2 正交试验实施流程图

4 实例计算与结果分析

4.1 太阳同步轨道设计实例

设目标区域中心O的经纬度为E121°,N23°,要求过该点的地方时为10∶00AM,卫星运行的轨道高度为500 km,取Re=6378.14 km,采用第2节的设计方法得到的卫星轨道参数见表2。

表2 卫星轨道参数

通过STK仿真获得该卫星轨道降交点部分星历数据如表3所示。

表3 卫星轨道降交点星历数据

由于降交点地方时基本恒定,任取表3中1组数据,由式(10)可计算得到此轨道降交点地方时约为9∶53∶11。

4.2 降交点地方时偏差计算结果

将表1中的偏差数据叠加到表2相关轨道参数中,根据图2中的计算流程计算当天、30天后、180天后、365天后、730天后降交点地方时与标称值9.8864小时间的偏差,也即漂移,结果如表4所示。

表4 不同时段降交点地方时偏差(单位:h)

表4中最后一行数据为各项入轨偏差为0时降交点地方时的漂移结果,也就是各种摄动因素导致的漂移,730天后的偏差为-0.0616 h,约为3.7 min,与前16组数据相比而言相当小,可见,入轨时的位置误差是导致降交点漂移的主要因素。从表4中单次试验结果可以看出,随着卫星运行时间的增加,降交点地方时漂移越来越大,其中第13次试验的漂移最大,在730天后达到1.5851 h。选取试验序号为1、6、11、16的数据绘制图形,如图3所示,从图中可以看出降交点地方时偏差在不同试验条件下呈发散状,并且随着时间的累积呈线性变化。可见,当卫星入轨位置偏差达到一定程度时,随着卫星运行时间的增加,将导致降交点地方时发生较大的漂移,这将严重影响对降交点地方时有要求的光学成像卫星的工作性能,这也是此类卫星轨道控制需要重点解决的问题。

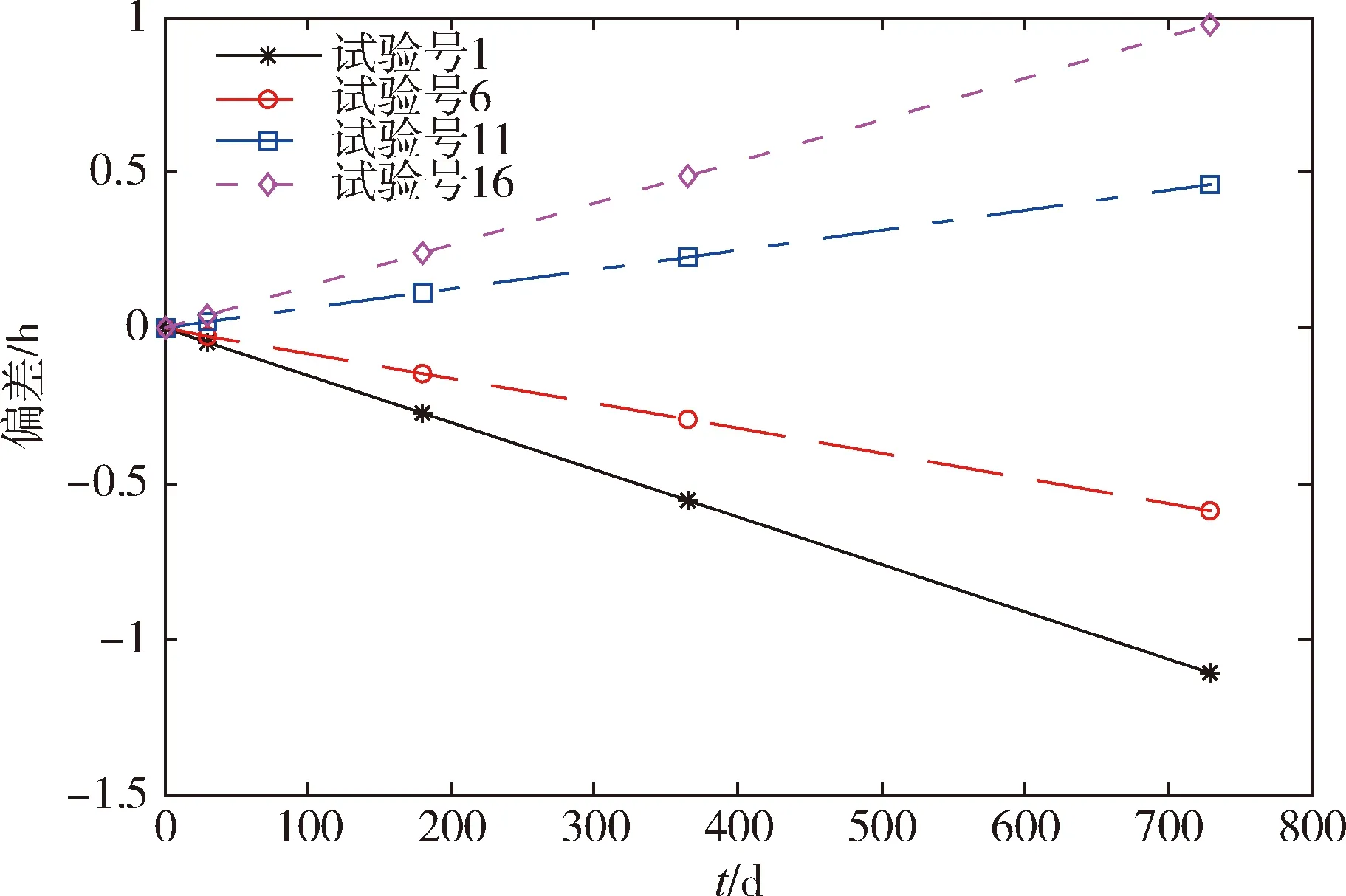
图3 降交点地方时偏差随时间变化图

4.3 相关性分析

两向量间的相关性可通过相关系数来衡量,对于向量x和y,其相关系数R定义如下:

(17)

5 结论

入轨精度是火箭性能的一个重要指标,卫星入轨后的轨道性能很大程度上由其决定。通过正交试验方法分析入轨精度对太阳同步轨道降交点地方时的影响,得到了轨道倾角偏差对降交点地方时影响最大的结论,为入轨精度设计与漂移主动控制等提供了依据,也为同类问题的分析评估提供了研究思路。