一种考虑最优收敛时间的多无人机编队控制方法*

何 印,张鹏飞,马振华,李亚文

1. 中北大学航空宇航学院,太原 030051 2. 中北大学智能武器研究院,太原 030051

0 引言

随着科学技术的发展,无人机技术开始应用于农田播种、森林搜救、边境监控、战场干扰、电子对抗等民用和军事领域。随着任务和环境的复杂变化,单一无人机已经难以满足任务的需求,由多个无人机组成的无人机集群因其高效率、高鲁棒、多功能及可扩展等优秀性能逐渐受到世界各国的重视。由于多无人机广泛的应用前景和巨大的作战优势,多无人机的编队控制技术研究成为当前的一个研究热点。

目前,对于多无人机编队控制技术的研究已经取得了部分成果,从控制结构上分为集中式、分散式以及分布式3种。其中,分布式控制结构中的一致性算法具备通信负载低、计算量小和鲁棒性强的优点,受到了国内外学者的广泛关注[1]。

针对多无人机的一致性编队控制研究问题,文献[2]提出了一种适用于高速多无人机编队的一致性控制算法,它能通过其他无人机的导航反馈来进一步控制编队队形。文献[3]针对包含无人机和无人车的异构多智能体系统,设计了基于模糊的滑模控制和一致性法相结合的控制方法,保证了编队的收敛性。文献[4]针对具有不确定参数的外部干扰影响的编队飞行问题,提出了基于多变量模型自适应控制的一致性控制方案。文献[5]用虚拟中心和一致性控制算法相结合,完成了四旋翼无人机的编队控制。

在多无人机编队控制技术的基础上,结合其他算法能够实现无人机的避障避碰控制。有学者将多无人机的避障避碰技术分为基于粒子群、蚁群、A*等优化方法、基于人工势场、速度障碍等势场避障方法以及基于机器学习的避障方法[6]。

其中人工势场法具有实现简单、反应快、适应性良好的特点,有学者将人工势场法和一致性控制算法结合,用于解决无人机的避障避碰问题。文献[7]针对多无人机躲避动态障碍物下的队形控制问题,在一致性控制与人工势场法的基础上,引入了碰撞预判机制,以减少不必要的避障行为。文献[8]提出了一种基于地球偏转力改进的人工势场法,并与一致性控制方法相结合,实现编队自组织避障。文献[9]提出了用一致性法和改进人工势场法实现多无人机在高速飞行过程中的避碰控制。文献[10]针对多无人机在三维障碍环境的避障和位置速度一致性问题,提出了基于协调增益和规划角改进的人工势场法和一致性法相结合的编队避障控制方法。该方法在避障避碰后,能够快速恢复预期编队队形。

上述文献提出的一致性编队控制和人工势场结合的控制方法充分考虑了无人机的避障避碰问题,但对无人机的机动约束问题缺乏考虑。

文献[11]通过增加无人机的机动性约束条件对一致性法进行了改良,并基于改良后的一致性法和粒子群优化算法,提出了不同初始条件下的无人机运动模型预测控制,实现了多无人机对静态障碍物和动态障碍物的高效避障能力。文献[12]基于一致性控制方法设计了两种编队成形策略,使多无人机能在约束条件下形成稳定的编队队形,并避免了机间碰撞问题。文献[13]针对无人机编队飞行规划问题,提出了一种基于多步粒子群优化的无人机编队航迹规划算法,该算法能够满足不同飞行阶段的约束条件,并能按照期望的航迹点进行编队飞行。文献[14]提出了一种基于虚拟领航策略的分布式模型预测控制算法,解决了在状态约束、输入约束、机间避碰、机间通信、避障等多种约束情况下的轨迹跟踪保持、编队队形保持。

上述文献提出的编队控制方法考虑了约束条件下的多无人机编队控制与避障避碰问题,但对考虑机动约束条件下的编队收敛速度缺乏相关讨论研究。

针对上述文献中的机动约束、机间碰撞以及编队收敛速度等问题,本研究基于粒子群优化算法对最优一致性控制进行速度优化,并融入人工势场思想,设计了用于实现最优收敛时间的编队控制方法,能够在机动约束条件下,提升编队的收敛速度,并避免无人机之间的碰撞。

1 坐标系及运动模型建立

本节首先描述无人机采用的坐标系及其运动模型,并根据实际应用环境约束机动参数,针对期望形成的编队队形,基于一致性理论优化运动模型,最后基于最优控制和粒子群优化算法改进一致性编队算法。

1.1 坐标系描述

传统的地面坐标系OgXgYgZg以地面上的某一点为原点Og,本文以某架无人机的初始位置为原点;Xg轴位于地平面内,指向某一方向;Yg轴与OXg垂直,处于地平面内;Zg轴与OgXgYg平面垂直,三轴的正向指向由右手螺旋定则确定,如图:

图1 地面坐标系

图中:将某时刻的无人机运动分解为X,Y,Z三个方向的速度分量。其中:Vxy为水平方向的合速度,φ为无人机的航向角。

1.2 无人机运动模型

基于上述建立的地面坐标系,本文采用常用的无人机运动学模型:

(1)

式中:(xi,yi,zi)为第i架无人机在地面坐标系中的位置,φi为第i架无人机的航向角,vxyi为第i架无人机在OXgYg平面内的速度,vzi为第i架无人机在OZg轴方向上的速度,axyi为第i架无人机在OXgYg平面内的加速度,azi为第i架无人机在OZg轴方向上的加速度,ωi为第i架无人机在OXgYg平面内的角速度。其中各个变量的变化范围如下:

(2)

对于整个多无人机编队而言,编队中的每架无人机在速度、加速度和角速度3个方面都需要满足相同的约束条件。

无人机在实际应用中,通常采用带自动驾驶仪的三自由度运动模型,本文根据文献[11]中对无人机运动模型的处理方法,基于多无人机的编队队形,采用了如下运动模型:

(3)

为了使多无人机形成期望编队队形,使用无人机之间的相对距离构建相对位置矩阵:

(4)

式中:[xij,yij,zij]为第i架无人机和第j架无人机之间的距离,当无人机形成编队队形时,需要满足以下条件:

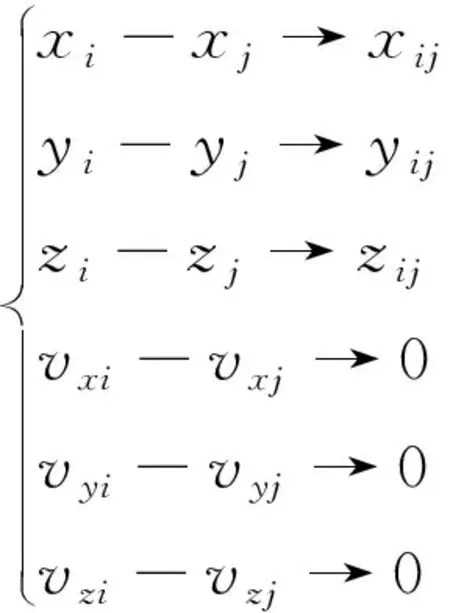
(5)

式(5)表明:当多无人机编队趋于队形稳定时,无人机之间的三维位置需要趋于式(4)的相对距离,无人机之间的速度需要趋于一致。

2 基于最优收敛时间的一致性编队控制方法

基于式(3)的运动模型结合最优一致性控制和粒子群优化算法,设计了一种基于最优收敛速度的一致性编队控制方法,该方法能在满足无人机运动约束条件下,使多无人机快速稳定地形成预期编队,并结合人工势场思想,实现编队过程中的无人机机间避碰能力。

2.1 编队一致性算法设计

为了使无人机的运动速度达到最优收敛,基于最优一致性控制和粒子群优化算法对无人机的飞行速度进行优化。文献[15]中将一阶最优一致性控制算法描述为:

(6)

式中:ωp,ωc分别为位置一致性权重和控制消耗权重。基于一阶最优一致性控制和式(3)的运动模型构建的最优一致性算法可表示为:

(7)

粒子群优化算法通过个体的信息共享来解决全局最优问题,本文以速度和加速度为参数,求解当前时刻的最优速度,其速度的更新模型可表示为:

(8)

式中:v(τ)和a(τ)分别代表τ时刻的速度和加速度,ωα为非负数代表惯性权重,c1和c2代表粒子收敛到相应状态的学习率,r1和r2代表0～1的随机数,pv和gv分别代表局部最优速度和全局最优速度。其算法流程如图2所示:

图2 粒子群优化算法流程图

图2中,对速度的优化总共分为7步:

1)确定优化的目标和参数;

2)利用当前的参数信息对粒子群进行初始化;

3)计算每个粒子的适应度;

4)按照公式更新速度和加速度,并根据约束条件进行优化;

5)根据更新速度后的粒子适应度计算个体最优值,随后与历史最优值进行比较,保留更优的个体最优值;

6)将最优值和群体历史最优值进行比较,保留更优的群体最优值;

7)判断迭代条件,满足迭代条件则结束当前优化,否则转第3步继续进行优化;

2.2 融入机间避碰的一致性算法优化设计

为了避免机间碰撞,本节通过人工势场思想设计机间避碰算法,当无人机间距小于安全距离时,增加无人机之间的排斥力,当无人机间距大于安全距离时,保持原状态飞行,如图示:

图3中:r为无人机的尺寸大小,R为避碰半径大小,ρ为无人机之间的距离。传统人工势场法的斥力模型如下:

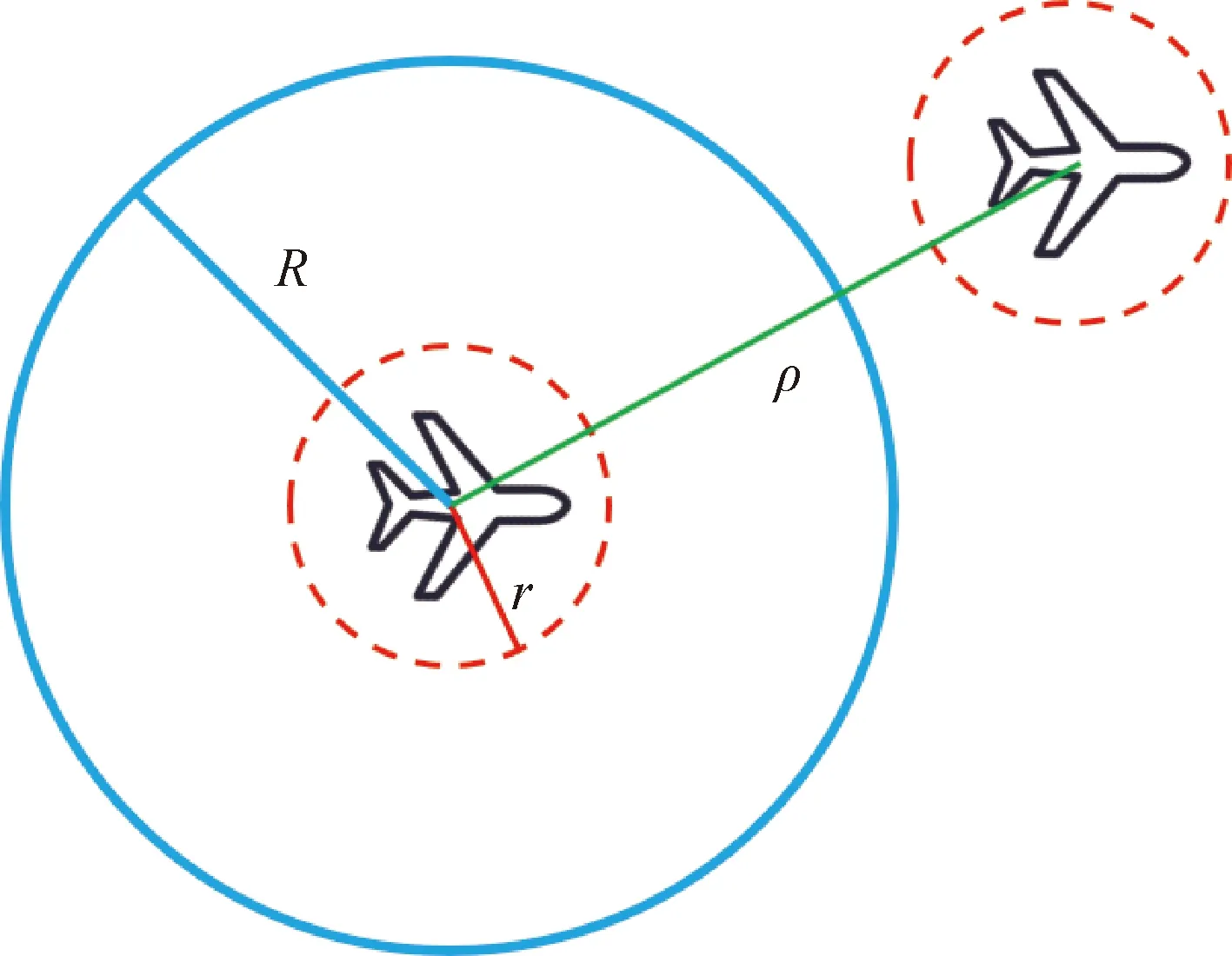
图3 机间避碰示意图

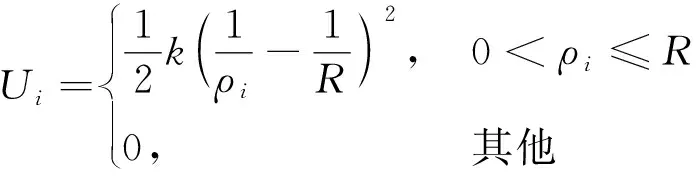
(9)

式中:k为斥力系数,ρi为无人机与障碍物的距离,R为避障范围。然而传统的斥力模型没有考虑无人机尺寸大小,无法直接应用于机间避碰。同时为了使避碰轨迹更加平滑,选用余切函数作为势场函数改进斥力模型,改进后的斥力模型如式(10)。

(10)

改进后的斥力模型充分考虑了无人机自身的尺寸大小和势场函数的优化。然而,还存在斥力方向与速度方向共线的局部振荡缺陷,如图4所示。

图4 机间避碰局部振荡示意图

图5 斥力方向改进示意图

图中:1号无人机到达1'号期望位置的速度方向和2号无人机对1号无人机的斥力方向共线,使其在当前位置不断往复振荡,无法形成完整的队形。为了避免这种情况,通过改变斥力方向,使其脱离局部振荡点,改变后的斥力方向如下:

图中:将局部振荡点的斥力减小θ角度后,使其脱离与速度方向的共线状态,避免局部振荡。最后,将机间避碰模型和最优一致性控制算法结合形成具有机间避碰的最优一致性控制模型:

(11)

3 仿真校验

以4架无人机组成方形队形为例,分别设计了具有机间避碰的一致性控制算法以及基于最优收敛时间和机间避碰的一致性控制算法2种案例进行对比分析编队控制效果、机间避障效果以及编队收敛效果。无人机的机动约束参数如下:

表1 无人机机动约束参数

4架无人机的通信拓扑邻接矩阵为:

(12)

期望编队队形的相对位置矩阵Rx,Ry,Rz分别为:

(13)

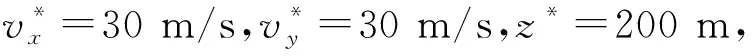
表2 无人机初始参数

图6 无人机飞行轨迹及机间距离图

图6显示了无人机的飞行轨迹,图6(a)中,无人机由于Z方向上的速度惯性,使无人机高度在轨迹前段部分超出预期值,随后逐渐降低,最终收敛于期望高度z*。图6(b)中显示了每架无人机之间的间隔距离,其中所有无人机的间隔均大于最小间隔,避免了机间碰撞的发生。随着时间变化,所有无人机之间的间隔距离逐渐满足式(13)所设定的期望编队间距。

图7～8为每架无人机的速度和加速度变化情况,其中所有无人机的速度和加速度都处于约束限制之内,并逐渐趋于一致。部分无人机的间距在0～5 s内越来越小,双方产生的斥力对其速度、加速度的影响较为明显,在5～10 s内由于水平速度达到期望值,其加速度骤然降低,并逐渐趋于0。

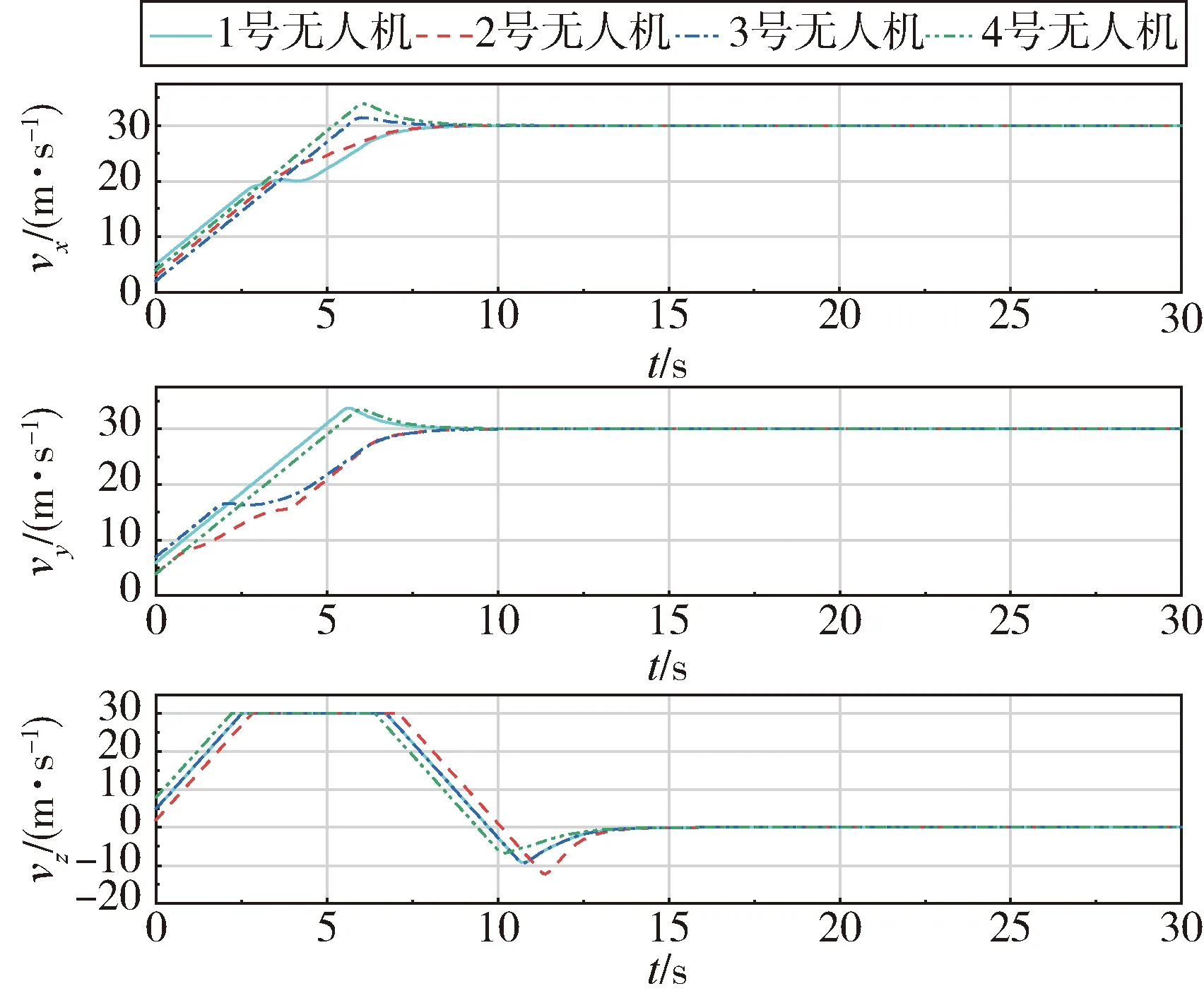
图7 无人机飞行速度变化图

图8 无人机加速度变化图

图9显示了整个多无人机编队的期望状态一致性收敛时间,其中优化后的控制方法使多无人机整体运动在17.9 s内达到了设定的期望误差之内,基础控制方法则在19.1 s内达到期望运动状态,两者相比优化后的方法使多无人机的编队收敛时间缩短了1.2 s,收敛性能提升了6.28%。

图9 多无人机整体收敛时间图

4 结论

针对多无人机编队的收敛时间问题,提出了一种基于最优一致性和粒子群优化的编队控制方法。通过与人工势场思想结合,建立机间势场函数,解决无人机之间的碰撞问题。与基础方法相比,该方法能使多无人机在约束条件下达到期望的运动状态,形成稳定的编队队形,并避免了无人机之间的碰撞,同时使多无人机编队的收敛时间缩短了1.2 s。最后通过仿真实验表明了该方法的有效性。