火箭定姿定点入轨的最优制导方法
王 健,刘星栋,支 晶
北京航天自动控制研究所,北京 100854
0 引言
随着载人航天工程的推进,为了更好地完成空间交会对接任务、快速准确地进行轨道交会过程,有效载荷对火箭入轨的精度提出了更高的要求,也促进了迭代制导技术的攻关,及其在载人运载火箭上的成功应用[1]。
在很多情况下,因有效载荷入轨后快速对地定向等需要,不仅要求运载火箭精确进入预定轨道,而且要求其满足一定的入轨姿态。但迭代制导技术在大幅提升运载火箭入轨精度及对故障适应能力的同时,带来了入轨姿态偏差散布较大等问题[2]。对带有姿态角约束的最优入轨问题,工程上一般通过增加一套独立的调姿系统来达到入轨姿态要求,但增加调姿系统会带来运载能力下降、可靠性降低等缺点,亟需研究更为通用可靠的制导算法解决这一问题[3]。
本文针对推力方向可变、大小不变的运载火箭,设计了一种定姿定点入轨的最优制导方法,通过对最优控制命题形式的转化,利用代数方法推导出可解的哈密顿方程组,实现了定姿定点问题的求解,并通过仿真验证了方法的可行性。
1 问题的提出
1.1 运载火箭质心运动方程的建立
先定义发射点重力惯性坐标系,原点Oi位于发射点,OiXi轴在水平面内,指向发射方向,OiYi轴垂直发射点水平面指向上方,OiZi轴与OiXi、OiYi构成右手坐标系。然后将坐标系原点Oi移到地心,就得到地心惯性坐标系。
真空中火箭受力情况比较单一,所受干扰主要是发动机及箭体结构的干扰,相对固定,发动机推力比较平稳。对真空二级上升段的运载火箭进行受力分析,忽略气动力影响,作用在火箭质心上的总外力Fs可以表示为[4]:
Fs=mg+P
(1)
其中:mg为作用在火箭上的地心引力矢量,P为作用在火箭上的发动机推力矢量。
g=-ω2r
(2)
认为火箭发动机推力大小不变、方向可调,则推力矢量可以表示为:
P=T·ib
(3)
其中:T为发动机推力大小,ib为推力方向矢量。
综上所述,在不考虑气动力影响的条件下,运载火箭在真空上升段相对于地心惯性坐标系的质心运动方程如下:
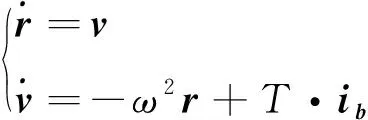
(4)
其中:r为火箭在该点的地心矢径;v为火箭在该点的速度矢量。
1.2 最优控制命题的建立
在地心惯性坐标系Oi-xiyizi中,建立了火箭的质心动力学方程(4),并依此建立最优控制命题。
由于火箭推力大小可变,状态变量为:
X(t)=[r(t),v(t)]T
(5)
相应的协态变量为:
λ(t)=[Pr(t),P(t)]
(6)
地心惯性系下的状态方程为:
(7)
其中:F为定常的推力;m0为初始质量;β为推进剂秒耗量,也是定常参数。
以燃料最省为性能指标:
(8)
由于秒耗量β为定值,燃料最省等价于时间最省,性能指标可以写作:
(9)
控制变量为推力方向:
ib(ibx,iby,ibz)T
(10)
其中:ibx,iby,ibz为推力在地心惯性坐标系下的分量。
控制变量有约束条件:
(11)
位置矢量初值:r(t0)=r0固定;
初始时间:t0固定;
位置矢量终值:r(tf)=rf固定;
速度矢量终值:v(tf)=vf固定;
终端时间(入轨时间):tf自由。

而且在规划飞行轨迹时,还可以使用该方法分析可控范围,以求解得出的v(t0)与任务要求相比,分析入轨姿态要求是否在可控集合的范围内。
2 最优控制问题的求解
2.1 控制量有约束问题转化为无约束问题

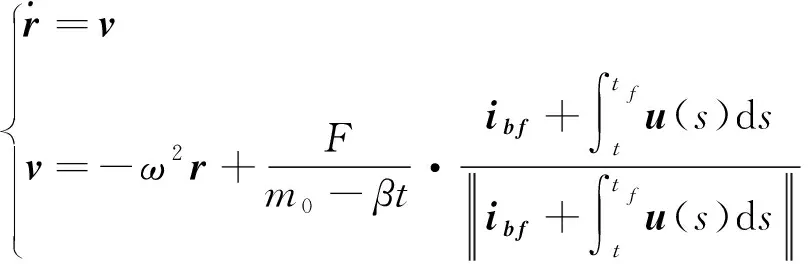
(12)
式中:控制变量为u(s),无约束。
记:
(13)
(14)
2.2 正则方程的求解
采用变分法,定义增广泛函为:
(15)
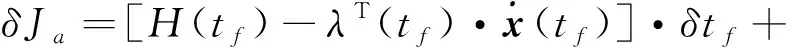
(16)
可得,
H(tf)=0
(17)
协态方程:
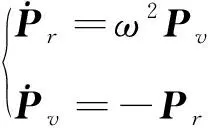
(18)
控制方程:
(19)
由式(19)可得:
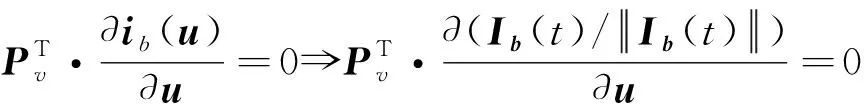
(20)
其中:
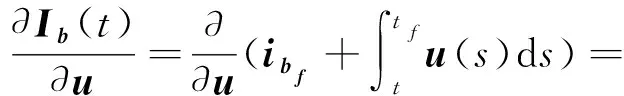
(21)
即
(22)
(23)
所以,
(24)
可得,
(25)
即,
(26)


(27)
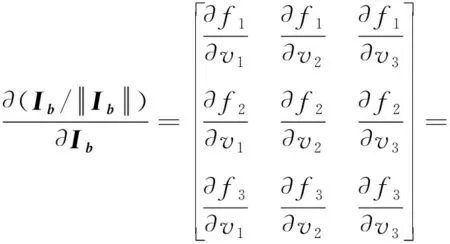
(28)
(29)
矩阵(28)的秩为2,故方程组(29)的解空间是一维的。
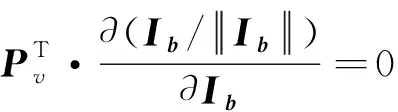
2.3 正则方程的求解
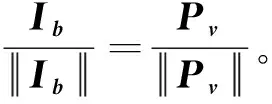
3 数学仿真验证
3.1 仿真场景
本文考虑某运载火箭二级真空上升段,以入轨进行空间交会对接的场景为算例对本文提出的最优制导方法进行验证。
3.2 仿真结果
本次数值仿真在MATLAB2010b环境中实现,采用内置Gauss伪谱法的SNOPT非线性规划求解器[6-7]求解协态变量。经过优化计算和连续仿真后得到火箭飞行最优控制曲线及相应速度位置变化曲线如图1~2所示。
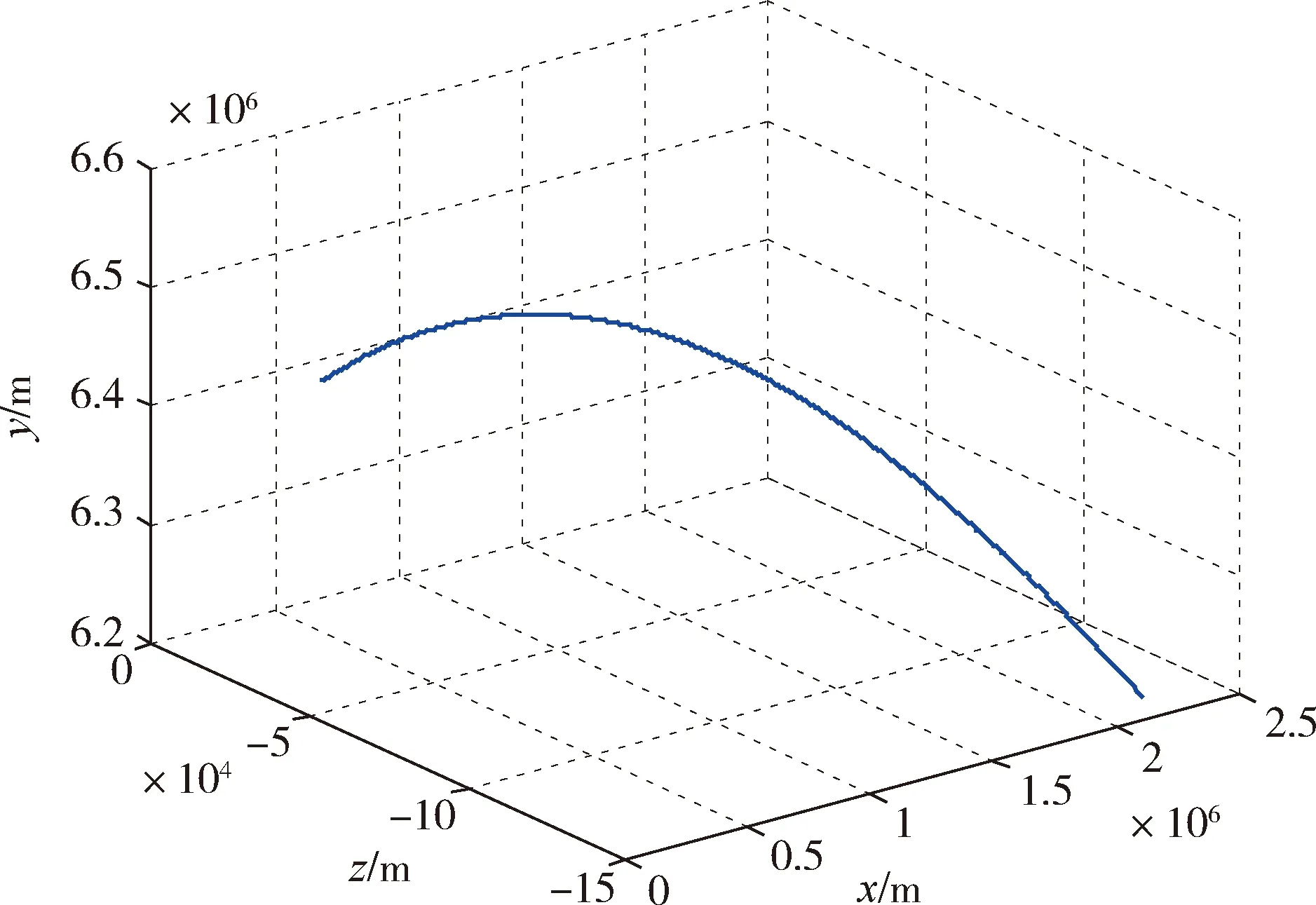
图2 位置
仿真得到入轨点速度位置及其与目标值的偏差见表3。

表1 模型参数
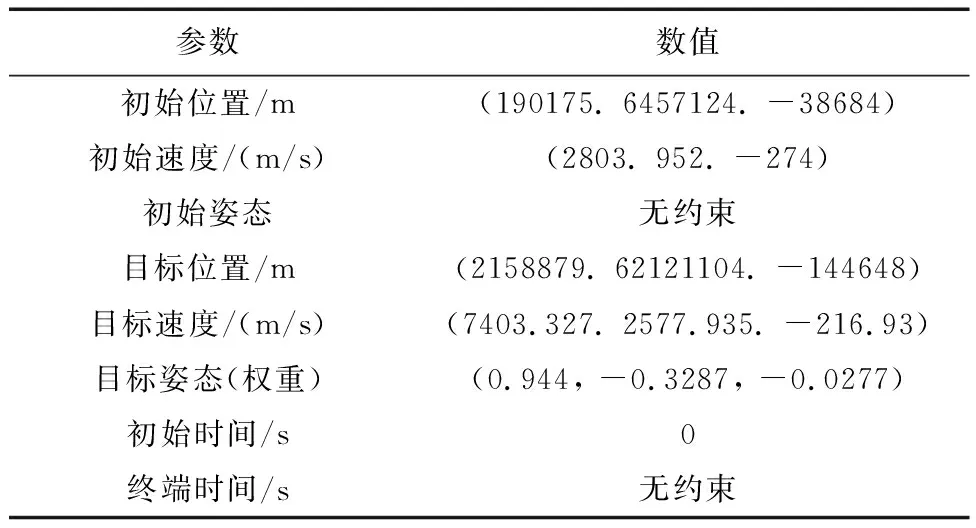
表2 端点约束

表3 入轨点速度位置偏差(tf=480 s)
由图1~2及表3中的仿真结果可以看出,在误差允许范围内,本文针对定姿定点入轨设计的最优制导方法能够使火箭在指定的地点以设定的姿态进入预定轨道。
4 结论
本文对火箭定姿定点问题进行了分析,建立了相应的最优控制命题。通过引入新的控制变量将命题转化为控制变量无约束问题,并利用变分法求得了一个可解的哈密顿方程组。通过伪谱法求得初始协态后可快速求得最优控制曲线。
经仿真验证,本文提出的最优制导方法可以解决定火箭定姿定点入轨问题,通过调节火箭的发动机推力方向,即可以使载荷从目标点以预定姿态精确入轨。

