主动卸载模式下嫦娥四号中继星轨道确定*
孔 静,胡国林,李 柯,李国强,刘俊琦,李皓皓,杨小锋
北京航天飞行控制中心,北京 100094
0 引言
无论在日地还是地月系统中,共线平动点都是引力系统的一个不稳定平衡点[1]。平动点航天器除受两个主要天体的引力外,还受到日心轨道偏心率、大行星以及太阳光压等引起的扰动影响,地面系统需要通过轨道维持确保航天器围绕其平动点运行[2-3]。
2018年5月21日发射的嫦娥四号中继星,2018年6月中旬进入绕地月L2点halo轨道,保障了月昼期间着落器和巡视器的对地通信[4-5]。为了节省航天器燃料消耗,马传令等人提出了轨道维持和动量轮卸载联合规划的方案[6],利用动量轮主动卸载实现轨道维持的目标。主动卸载模式指的是在动量轮达到饱和前,通过规划航天器的卸载时刻、卸载姿态和速度增量等实现航天器轨道构型保持控制目标的卸载方式。工程应用时,嫦娥四号中继星大约每3~4 d卸载一次,每次卸载规划的速度增量为1~2 cm/s。频繁的机动、高精度的控制要求提供高精度的定轨支持。
第1次实现绕地月拉格朗日点运行的是美国的THEMIS任务。该任务由5个地月空间探测器组成,在延寿阶段安排了其中两个相同的航天器B、C开展月球及其更远空间的环境拓展探测和工程验证,拓展任务改名为ARTEMIS。2010年8月和10月两个探测器分别进入地月L2点和L1的Lissajous轨道。得益于全球布站和高精度的测量,在不考虑卸载影响的条件下,实现了位置0.1 km和速度0.1 cm/s的轨道确定精度[7]。我国的CE-5T1拓展任务中,服务舱在距离月球约6×104km的地月L2点Lissajous轨道飞行约40 d,成为我国第1颗绕地月L2点飞行的探测器。黄勇等人综合利用5~7 d的测距测速和VLBI数据,航天器定轨的位置和速度精度分别为百米和mm/s量级,考虑卸载的速度误差为1 cm/s[8]。段建锋等人通过对嫦娥四号中继星光压的精确建模,在中继星+Z轴对日和非对日运行状态下,分别实现重叠弧段0.6 km和1.6 km的位置误差以及3 mm/s和8 mm/s的速度误差[9]。
上述工作对卸载力的解算主要采用轨道坐标系或是天球参考系下的匀加速模型,该处理模型在观测几何较差条件下易出现卸载加速度解算不准确、定轨预报精度低等问题。针对该问题,本文提出了嫦娥四号中继星主动卸载模式下的轨道确定方法,通过引入姿态信息的卸载力建模与解算,提高定轨和预报精度。
1 卸载原理与建模
1.1 卸载原理
动量轮控制主要是利用作用力和反作用力的原理,当外在的干扰力作用在航天器上产生干扰力矩时,安装在航天器相应位置的动量轮通过提高转速增加动量去抵抗干扰力矩的影响。当动量轮转速达到门限值时通过喷气抵消干扰力矩,同时释放累积的动量。
嫦娥四号中继星在本体系的三个轴各安装了1个动量轮,同时在三轴合成动量的反方向斜装了1个动量轮,即采用由偏置动量轮组成的整星零动量方案进行姿态控制。偏置动量轮作为备份,角动量保持稳定,一般不参与控制。
中继星卸载主要通过安装在各个方向的12台姿控发动机实现[4]。卫星姿控发动机的布局如图1所示,控制中继星zb轴角动量卸载的发动机(6A/6B、5A/5B)为力偶发动机,喷气卸载时不产生zb方向推力;控制xb和yb轴角动量卸载的发动机为非力耦发动机(3A/3B、4A/4B、1A/1B、2A/2B),喷气抵消角动量的同时,产生+zb方向推力。姿控发动机布局、卸载控制方式决定嫦娥四号中继星卸载的速度增量主要集中在本体系+zb方向,在此基础上本文提出主动卸载模式下嫦娥四号中继星halo轨道定轨精度确定方法。

图1 卫星姿控发动机布局
1.2 主动卸载力建模与应用
由于航天器的运动通常在惯性系下描述,因此对卸载产生的加速度建模主要采用等效的匀加速度模型[10-12],即假设在一次卸载周期内,卸载产生的加速度在惯性系3个方向恒定,通过解算3个方向的经验力等效卸载过程,模型没有考虑实际推力的方向和大小。嫦娥四号中继星卸载产生的推力集中在本体系+zb方向,由于是主动卸载,卸载的时刻和姿态作为规划量是已知的。一组典型的主动卸载过程如图2所示,航天器在卸载前将姿态调整至卸载的目标姿态,卸载完成后根据需要再次调整姿态。假设在卸载过程中航天器姿态保持稳定,利用姿态转换矩阵将惯性系下3个方向的卸载分量转换到本体系上,通过求解本体系1个方向的经验力吸收卸载带来的速度增量。

图2 典型主动卸载过程和定轨使用积分器情况
通过姿态四元数建立惯性系到本体系的旋转矩阵M。
假设刚体的姿态Q=[q0,q1,q2,q3],根据欧拉定理[13],绕参考系转轴转过角度r的矩阵表示为M,那么
(1)

计算得到旋转矩阵为
(2)
在惯性空间下
(3)

(4)
由于本文的方法只涉及本体系+Zb方向的加速度,得到惯性系加速度对本体系Zb方向加速度的偏导数模型为
(5)
1.3 积分器的使用
在轨道积分过程中,一般采用的是多步法定步长的Krogh-Shampine-Gordon(KSG)积分器,对于卸载前的轨道,一般采用定步长积分法,积分步长通常设置为30 s。卸载周期通常很短,从卸载发生到恢复稳态的时间小于1 min,卸载导致卫星轨道速度差异明显,卫星运动方程的右函数值变化较大,对于摄动力变化剧烈的卸载过程,需要根据截断误差自动调整积分步长,以保证积分精度,提高卸载加速度解算准确度,适宜采用单步法积分器。卸载完成,在满足精度要求之后应继续采用大步长的定步长积分法以减少计算量。本文选用了KSG积分器与Runge-Kutta-Fehlberg(RKF)积分器相结合的星历积分方法。在平稳飞行阶段,采用KSG积分器,在调姿卸载阶段采用RKF单步法积分积分器。图2给出了卸载过程对应的积分器使用情况。
2 数据处理
2.1 数据概况
2022年4月23日和5月20日,中继星分别进行了2次轨道维持,间隔27 d,期间规划完成6次主动卸载。4月23日轨道维持后中继星姿态由+zb轴对日转入+zb轴对月,用于着巡器的中继通信服务,5月8日完成中继通信服务后转入+zb轴对日姿态,5月11日主动卸载后转入+xb轴惯性对日姿态,5月14日重新转入+zb轴对日姿态。
本节选取2次轨道维持之间的跟踪数据进行处理。5月18日前,中继星主要有佳木斯、喀什和阿根廷3个深空站以及喀什、青岛和纳米比亚3个18 m站进行跟踪,每天的跟踪弧长在8 h左右,18日后主要由3个深空站进行跟踪,每天的跟踪弧长约4 h。选取分析包括双程测距和双程测速两类数据。测量数据分布如图3所示,图中同时标记了主动调姿卸载的时刻,表1提供了具体的卸载信息。
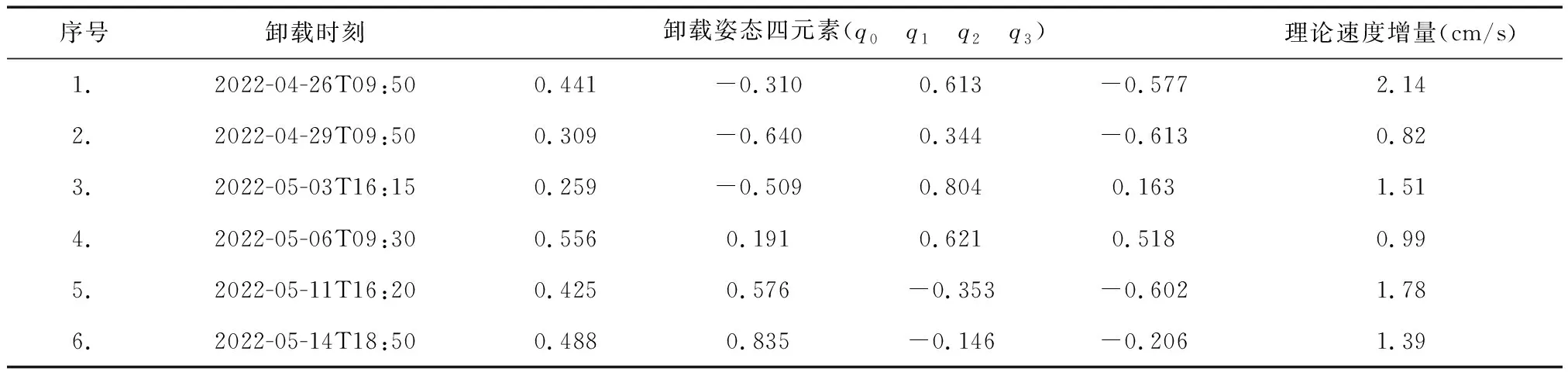
表1 卸载信息统计

图3 测站跟踪分布图
从图3中可以看出,卸载的频率间隔为3~5 d,卸载全部在佳木斯深空站跟踪弧度内完成。第5次与6次卸载之间只有阿根廷和佳木斯两个深空站进行跟踪,其他两次卸载之间均有3个以上测站完成跟踪测量。
2.2 数据处理
嫦娥四号中继星halo轨道的周期约为14 d,仅使用卸载后的数据进行轨道确定的速度精度在厘米量级,无法满足主动卸载对定轨精度的要求。为了提高速度解算精度,需联合卸载前后的数据,对卸载过程进行经验力建模。表2为定轨计算的基本策略。对于地月L2点halo轨道,由于测距系统差和轨道之间的相关性较强,在解算测距系统差时需对系统差加约束进行求解。

表2 精密轨道解算策略
为了评估卸载解算效果,精密轨道通过6~7 d的数据解算1组经验力获取,同时评估精密轨道精度。
每次卸载后需要快速轨道重建,以评估卸载效果和规划下一次卸载策略,将数据截断至卸载后1.5 d,定轨预报至下一次卸载前,评估定轨预报精度。
上述方案分别使用解算惯性系3个方向经验力和只解算本体系+zb方向经验力两种方法计算并对结果进行比较。
2.3 精度评估
2.3.1 精密轨道精度评估
使用弧段内所有的测距和测速数据进行轨道确定,由于测速数据对halo轨道定轨精度的改进量较小,表3统计了测距数据的RMS和形式误差,同时给出了解算的速度增量。

表3 卸载解算情况统计
两种方法解算的测距数据RMS大小相当,由于本文提出的方法在经验力解算中仅解算1个参数,解算参数的减少降低了参数之间的相关性,该方法形式误差明显优于解算3个方向经验力的做法,解算的速度增量也更接近理论值。
使用重叠弧段比较的方法对精度进行评估,将相邻两个精密轨道的重叠部分做比较,统计位置和速度误差,结果如图4所示。

图4 精密轨道评估
从图4可以看出,改进后的重叠弧段位置精度小于1 km,速度精度优于4 mm/s(除第5组),明显优于改进前的精度。第5组的精度略差,主要是由于在5月11日、14日主动卸载后进行了姿态调整,调整前后光压受摄面积发生变化,一个方向的卸载解算模型不能很好吸收这部分误差导致的。这也表明该方法的使用依赖准确的姿态信息。如果姿态信息不完整,或是信息不准确,则传统的3个坐标分量一并解算更有利于轨道精度的提升。
2.3.2 预报精度评估
图5给出了使用卸载前数据和卸载后1.5 d数据进行定轨预报至下一次卸载前的轨道预报精度,除第5组外,其他弧段使用改进后的方法的精度明显提高,预报2~3 d至下一次卸载前的位置精度为1.2 km,速度精度优于5 mm/s,相对于改进前精度提高约1倍。

图5 定轨预报精度评估
3 结论
对嫦娥四号中继星halo轨道主动卸载模式下的定轨预报精度进行了讨论,提出了结合中继星姿态控制信息解算卸载经验力的轨道确定方法。相比传统的解算方法,该方法形式误差明显降低,对轨道的约束增强,解算速度增量的准确度提高,基本结论如下:
1)主动卸载模式下嫦娥四号中继星定轨的位置精度优于1 km,速度精度优于4 mm/s;预报2~3 d至下一次卸载的位置精度为1.2 km,速度精度优于5 mm/s。
2)由于该方法需要引入姿态信息进行建模和计算,在姿态信息不完整或卸载前后姿态不一致的情况下,会影响解算效果,存在导致定轨预报精度降低的可能。

