压轴题的解题策略初探——以近几年安徽中考压轴题为例

汪文龙

（安徽省合肥一六八玫瑰园学校东校区，安徽 合肥 230601）

在解题教学特别是压轴题的讲解中，由于个人理解或经验的原因，部分教师只是就题讲题，或者讲解某一类题型的方法。而对压轴题的整体思考策略讲解甚少，系统指导欠缺，导致学生面对陌生的题目或题型不知所措，得分较低。笔者以近几年安徽中考部分压轴题为例，在分析解法的基础上，系统探究压轴题的解题策略。

一、巧用模型，熟悉知识联结点

在平时的解题过程中，我们几乎不可能想出一道全新的题目，它和以前解过的题目既不相像，又无联系。因此我们需要注意积累常见模型和基本解题方法。比如在近几年安徽中考题中常见到的“隐圆问题”“旋转模型”“最值问题”等。掌握基本模型的图形特征以及解决方法，将大大提高我们的解题效率。

（一）巧用模型

下面以2016 年安徽中考选择压轴题第10 题为例，讲解“隐圆问题”的本质及其应用。

题目：如图1-1，Rt△ABC 中，AB⊥BC，AB=6，BC=4。P 是△ABC 内部的一个动点，且满足∠PAB=∠PBC。则线段CP长的最小值为（ ）。

图1-1

分析：由条件∠PAB=∠PBC 及AB⊥BC 可知∠APB 为直角，这是“隐圆问题”的特征之一。由直径所对的圆周角是直角可知，点P 在以线段AB 为直径的圆上，又因为P 是△ABC 内部的一个动点，所以点P 为劣弧BD 上一动点（如图1-2）。此题转化为点C 到劣弧BD 上点的距离的最小值，即点到圆的最值问题。连接圆心O 和点C 交⊙于点P1，则CP1的长度即为所求线段CP 的最小值（如图1-3）。

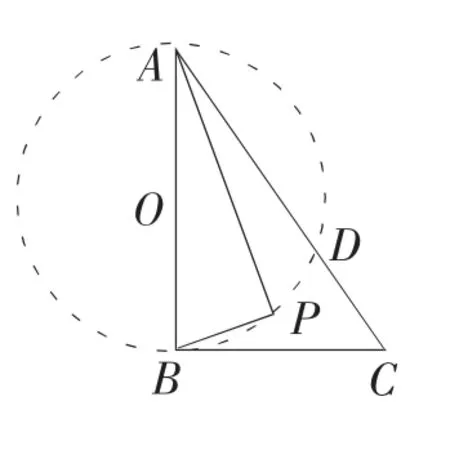
图1-2

图1-3

本题归为“隐圆问题”的依据是，动点作为顶点的一个角为直角。理由是，在圆中，直径所对的圆周角是直角。除此以外，还有其他条件也是“隐圆”的特征，限于篇幅，本文仅给出以下两个：

1.若从一个顶点O 出发的两条线段相等，则这两条线段的另外两个端点在以O 为圆心，以线段长为半径的圆上。理由是同圆中，半径相等。

2.若凸四边形的一组对角互补，则该四边形的四个顶点共圆。理由是，圆内接四边形的对角互补。

根据以上特征，可以把所求问题转化为与圆有关的问题进行解决。大大降低了解题难度。

（二）熟悉知识联结点

不过，对于灵活多变的题目，一些基本模型还远远不够，特别是对于图形比较复杂、不易看出其中隐含的基本模型的问题。因此，在解题时应排除无关干扰，抽离出简单模型。这就需要我们在平时的学习和解题过程中，熟悉各知识点之间的联系，而这也是解题的关键。

中考压轴题考查得比较灵活，究其原因，在于知识点之间的联系比较多且密切，学生不易想到。而这其中，重点知识又起着举足轻重的作用。比如中点可以与平行、等腰三角形、直角三角形、角平分线等结合在一起。这些重点知识将不同的知识点联系在一起，导致考查角度非常灵活，难度增加，方法也变得多样。

下面以2014 年安徽中考填空压轴题第14 题为例，详细讲述知识点之间的联系在解题中的应用。

题目：如图2-1，在平行四边形ABCD中，AD=2AB，F 是AD 的中点，作CE⊥AB，垂足E 在线段AB 上，连接EF、CF，则下列结论中一定成立的是________（把所有正确结论的序号都填在横线上）

图2-1

分析：本题的难点在于辅助线的添加不知从何而想。如果熟悉了中点与其他知识点之间的联系，辅助线的添加将迎刃而解。与中点这一知识点有关的考查方式有以下几个：

1.中点+ 中点：考查中位线；

2.中点+ 直角：考查直角三角形斜边上的中线的性质；

3.中点+ 等腰三角形：考查等腰三角形三线合一的性质；

4. 中点+ 平行：考查中位线或考查“X”型全等。

题目中的结论①较简单，这里不再赘述。

由AB∥CD 以及中点F，符合上述4第二小点，可以联想出补全“X”型全等，即分别延长EF 和CD 交于点G（如图2-2）。此时由全等得EF=FG，即点F 是EG 的中点，然后在Rt△ECG 中解题。

图2-2

而由平行及CE⊥AB 可知，∠ECD=90°，由中点F 以及∠ECD=90°，符合上述2，也可以联想出补全直角三角形ECG（添加辅助线同上），利用直角三角形斜边上的中线的性质可知EF=CF。

以上两点均可提示我们作出辅助线证明结论②。

对于结论③，因为考查面积的关系，且两三角形有公共边EC，则可以想到过点F 作FP⊥EC 于点P，再由条件可知FP∥CG。由点F 是EG 的中点以及FP∥CG，符合上述（4）第一小点，得出又CG≠BE，可知结论③不对。

结论④可由①②推导出。

由以上分析可知，本题的突破口是中点及其他知识点之间的联系。而整个解题过程也都围绕着中点这一知识点。因此，熟知一些重要的知识点以及它与其他知识点之间的联系，对于我们找到“突破口”至关重要。

二、重视联系，深挖方法延续点

对于安徽中考试卷中的最后一题压轴题，一般都有两到三个小问题。这些问题串之间，除了难度递增，还有更为重要的联系。比如，前面几问的结论或者解题思路，在解决后面的问题时常常用到；将方法特殊化、一般化，可以处理后面的问题；前面几问中，看似不重要的一些推论，在解决问题时往往也能起到关键的作用。因此，重视问题串之间的内在联系，深挖方法之间的延续点，将为我们解决最后一问，提供重要的线索。

下面以安徽中考2018 年压轴题的第23 题为例，具体阐述各小问之间的联系在解决难题中的表现。

题目：如图3-1，在Rt△ABC 中，∠ACB=90°，点D 是AC 上的一点，点M平分线段BD，作DE⊥AB 于点E，CM 的延长线交边AB 于点F。

图3-1

1.求证：CM=EM；

2.如果∠BAC=50°，求∠EMF 的大小；

3.如图3-2，如果△DAE≌△CEM，且点N 平分线段CM，求证：AN∥EM。

图3-2

分析：第1 问利用直角三角形斜边上的中线的性质得出CM=EM=DM=BM。第2 问利用1 的结论，再利用等边对等角得出角的关系，最后通过外角和邻补角知识计算求出∠EMF 的大小。

第3 问难度较大，由条件△DAE≌△CEM 以及第1 问结论CM=EM=DM=BM 可以推导出△AED 和△CME 均为等腰直角三角形，△DEM 为等边三角形。但点N 为CM 的中点这一条件不知怎么使用。不过，我们由第2 问的解答方法可以得出以下两种不同的思路：

第一种：类比第2 问的解题方法，我们可以求出∠EMF=90°，若要证AN∥EM，则需证∠ANM=90°，即AN⊥CM，又点N为CM 的中点，此时只需证AN 是线段CM的中垂线即可。根据常用方法，连接AM（如图3-3），只需证AC=AM 即可。

图3-3

根据第2 问及前面的思考过程，我们一直在利用角的计算推导，所以此时很容易想到，通过证∠ACM= ∠AMC 求出AC=AM，由前面可得AE=EM=CM=BM，∠EBM=∠MEB=180°-∠AED-∠DEM=30°，由AE=ME，得∠AME=15°，∠CBM=∠ABC-∠EBM=15°。由CM=BM 得∠CBM=∠BCM=15°，又∠ACB=∠EMC=90°，所以∠ACM=∠AMC，得证。

第二种：第2 问是利用角的计算推导得出，类比之，第3 问能否利用线段的计算推导呢？因为由前面的推导我们已经得出了大量的相等线段，此时点N 为CM 的中点这一条件或许可以用上。假设CN=MN=x，我们得出CM=EM=AE=2x，由∠MEF=30°，可知通过计算可得又∠AFC 为公共角，所以△EFM∽△AFN，所以∠ANF=∠EMF，所以AN∥EM，得证。

《义务教育数学课程标准（2022 年版）》指出，归纳概括得到的猜想和规律并加以验证是创新的重要方法。其中，类比是发现规律很常见的方法。由以上分析可知，两种思路的获得都与前两问的结论和方法密不可分，特别是第2 问思路的延续和类比，至关重要。

三、大胆猜想，关注条件特殊点

人们常说，仰望星空和脚踏实地同样重要。在数学解题中，猜想和验证亦是如此。在讨论数学问题时，特殊化比一般化起着更为重要的作用。大多时候，我们没有寻找到一个问题的答案的原因，就在于这样的事实。对于毫无头绪的题目，可以根据题中的特殊条件进行猜想，我们也可以把这称为几何直观，这本身也是新课标考查的核心素养之一，然后再通过演算或推理来验证它的正确性。在解题过程中，猜想能为我们解题活动的开展指明方向，而演算和推理则可以使猜想落地生根，变得有意义。猜想要敢想，大胆猜想。而演算则需真算，小心求证。

对于中考压轴题而言，重点知识可以将不同的知识点联系起来，增加灵活性，而特殊条件则可以提高知识点考查的深度，同样可以提高试题的质量。而这些特殊的条件，则往往是我们猜想的巨大源泉。

下面以2016 年安徽中考压轴题第23 题为例进行阐述。

题目：如图4-1，A，B 分别在射线OM，ON 上，且∠MON 为钝角，现以线段OA，OB 为斜边向∠MON 的外侧作等腰直角三角形，分别是△OAP，△OBQ，点C，D，E 分别是OA，OB，AB 的中点。

图4-1

1.求证：△PCE≌△EDQ；

2.延长PC，QD 交于点R。

①如图4-2，若∠MON=150°，求证：△ABR 为等边三角形；

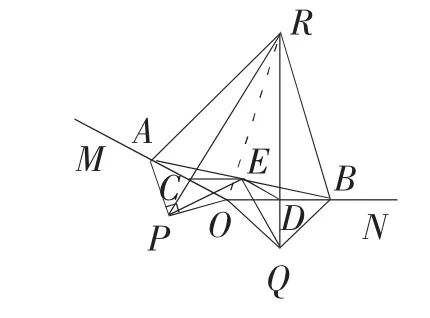
图4-2

图4-3

分析：第1 题利用中点及相关的性质即可解决，此处不赘述。第2 题的①问根据中垂线的一般思路，连接OR（如图4-2），得AR=OR=BR，在四边形CODR中，由∠MON=150°得∠CRD=30°，所以∠ARB=60°，得证。

第2 题的②问中，一般初中阶段所求的角都是特殊角，比如30°，45°，60°，90°等。因为∠MON 为钝角，且由图点P，O，N三点很像共线，因此猜测∠MON=135°。跟45°有关的线段比值为则猜想若∠MON=135°，由第2 题的①问思路可得∠ARB=∠PEQ=90°。此时，我们只需证∠PEQ=90°即可。由第1 题问可知DE∥OA，则∠CED=∠ACE，又由△PCE≌△EDQ 可知，∠DEQ =∠CPE。所以∠PEQ=∠CED-∠CEP-∠DEQ=∠ACE-∠CEP- ∠CPE= ∠ACE- ∠RCE=90°，再由第2 题的①问的思路可以得出∠MON=135°得证。因此，点P，O，N 三点共线则

通过以上分析，我们不难发现，猜想出∠MON=135°是本题的一个突破口。虽然在求证∠PEQ=90°时仍有难度，但却为我们指明了思考方向。当然，大胆猜想不一定都对，而猜想的这一特点更能体现出小心求证的重大作用。当然，有效地应用合情推理是一种实际技能，并且像任何其他实际技能一样，要通过模仿和练习来学会它。

四、结语

巧用数学模型，让我们知道如何解决一般的压轴题；掌握重点知识点，让我们了解了题目的变化方式；而关注特殊条件，则能让我们的思维插上想象的翅膀，找到问题解决的关键点。需要指出的是，压轴题考查的是学生的综合能力。因此，各种策略的使用不是孤立的，而应是相互配合，你中有我的关系。同时，面对难度很大的压轴题时，敢于尝试的勇气和解决难题的“渴望”心态也常常会带来很大的惊喜。