强基计划数学备考系列讲座(19)——复合最值及其探求策略

王慧兴(正高级教师 特级教师)

(清华大学附属中学)

1 知识要点

1.1 基本概念

以双变量函数f(x,y)为例,给定x∈D1,当y∈D2时,若f(x,y)有最大值M,则这个M与x的值有关,是x∈D1的一个函数M＝M(x),再让x∈D1,如果M存在最小值Mmin,则

通常称之为一种复合最值,其中M称为内层最值,或“内层最值函数”.复合最值也有其他形式,譬如

1.2 探求策略

探求复合最值的根本策略是基于内层最值的概念,选择数值或函数插值,组合常数,按均值适度放缩,探求目标.

1.3 不可换序

复合最值与最值顺序有关,通常不可以交换.譬如根据函数图像位置关系(如图1),可得

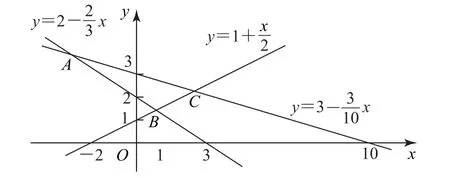
图1

2 典例精析

高校强基计划校考笔试经常立意复合最值试题,在高考试题中也多次出现复合最值试题.

2.1 基于内层最值概念,构建内层最值函数,转化为单变量函数,探求目标

2.2 选定主元,辨别性质,合理定位,按均值放缩,探求目标

探求一个复合最值,关键是基于内层最值概念,先固定一个变量,以另一变量为主元,转化成一个单变量函数M.根据这个单变量函数的特性——单调性与凹凸性,定位内层最值,缩小包围圈,建立内层最值函数M.例1表明,这个内层最值函数往往是分段的,这体现最值问题探究过程中的分类讨论思想,这种分类讨论常常可以通过“平均值组合”求解.

例2 同例1.

2.3 舍弃干扰项,合理取舍,组合常数,按内层最值与均值放缩,探求目标

2.4 按内层最值概念,均匀插值,化无限为有限

例6 (清华大学)已知函数f(x)＝|x2＋a|＋|x|(x∈[－1,1]),记f(x)的最大值为M(a),求M(a)的最小值.

由对称性,只需考虑x∈[0,1],由内层取最大值,均匀插值,得

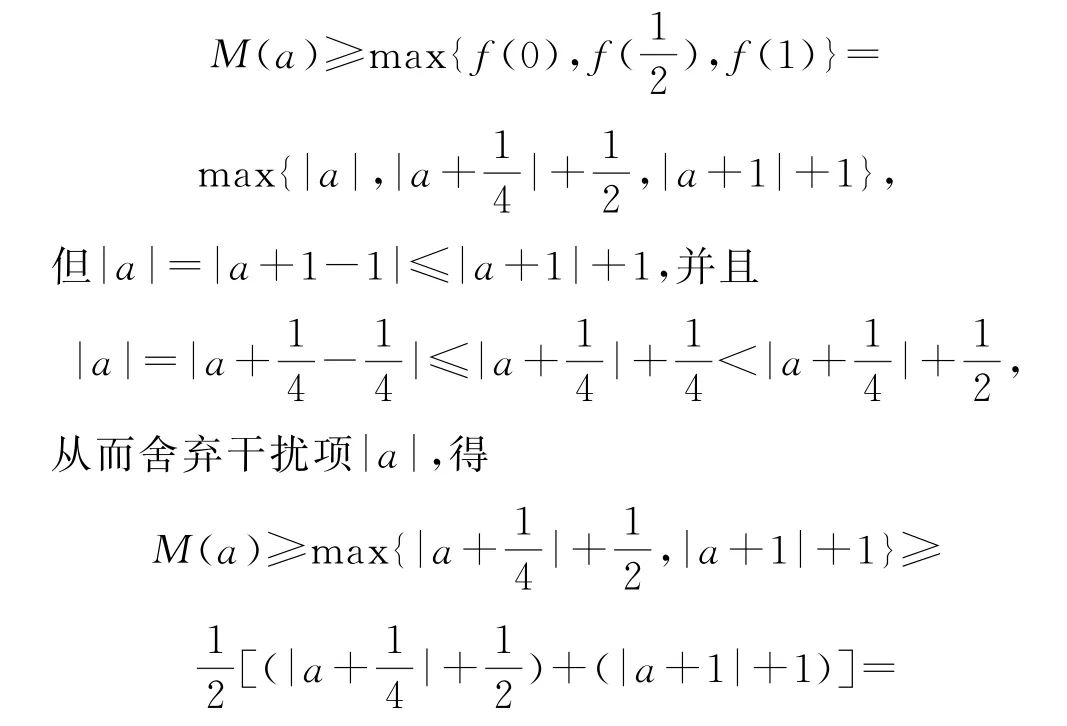
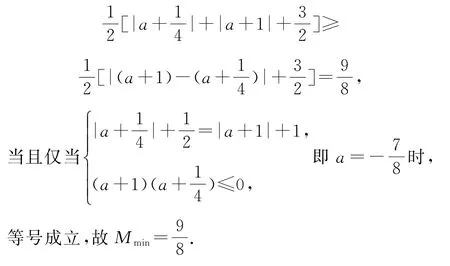
2.5 分析极端性,合理插值,化无限为有限

2.6 基于内层最值布列不等式,按均值放缩,构建目标

例8 给定正数a,b,c,记,a＋b2＋c3}＝M,当正数a,b,c变化时,求Mmin.

由内层最值,得

解得M≤3,当且仅当时,有

2.7 综合问题中的复合最值探求

2.8 探求组合问题中的复合最值

例11 10个人到书店买书,已知:

(1)每人都买了3本书;

(2)任何两个人所买的书中,都至少有一种相同.

问:购买人数最多的一种书最少有多少人购买?

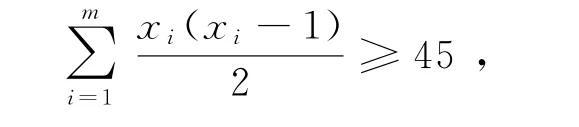
所以

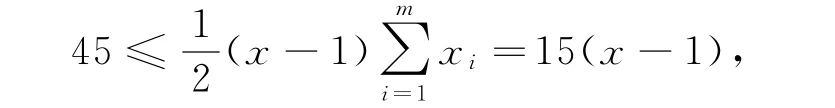
即x≥4.如果x＝4,则所有xi＝4(i＝1,2,…,m),与矛盾,所以x≥5.

构造:记Bi为互不相同的书,当x＝5时,存在购买人数最多的一种书恰有5人购买的情况如下:

故购买人数最多的一种书最少有5个人购买.

2.9 应用问题中的复合最值探求

例12 某企业接到生产3000台某产品的A,B,C三种部件的订单,每台产品需要这三种部件的数量分别为2,2,1(单位:件).已知每个工人每天可生产A部件6件,或B部件3件,或C部件2件.该企业计划安排200个工人分成三组分别生产这三种部件,生产B部件的人数与生产A部件的人数成正比,比例系数为k(k为正整数).

(1)设生产A部件的人数为x,分别写出完成A,B,C三种部件生产需要的时间;

(2)假设这三种部件的生产同时开工,试确定正整数k的值,使完成订单任务的时间最短,并给出时间最短时具体的人数分组方案.

(1)设完成A,B,C三种部件的生产任务需要的时间(单位:天)分别为T1(x),T2(x),T3(x),由题设有

其中x,kx,200－(1＋k)x均为1 到200 之间的正整数.

(2)设完成订单任务的时间为

3 实战演练

(完)