钢管高强灌浆料翼缘-波纹腹板曲梁抗剪性能分析

江东，邵永波，邓利霞，杜栖云

（西南石油大学 土木工程与测绘学院，成都 610500）

波纹腹板梁为普通工字型钢梁的改进形式而被广泛用于桥梁、房屋和工业厂房等结构中。波纹腹板的波折外形增加了平面外高度，从而在腹板厚度较小时依然具有较大的平面外刚度及较高的抗剪屈曲承载能力[1-3]。Yi等[4]采用数值计算方法研究梯形波纹腹板的剪切破坏模式时发现，梯形波纹腹板受剪时可能会发生3种不同的屈曲模式失效：局部屈曲、整体屈曲和耦合屈曲，并在参数研究基础上提出了耦合屈曲承载力计算公式。对于波纹腹板的各种屈曲失效，国内外很多学者进行了相关研究。李时等[5]对波纹腹板梁在剪力作用下的破坏机理及基本性质进行了理论分析。李国强等[6]采用数值分析方法研究了波纹腹板H型钢梁的抗剪性能，并以板的稳定理论为基础提出了波纹腹板局部屈曲和整体屈曲的弹性极限强度以及剪切承载力计算公式。Sause等[7]提出了梯形波纹腹板发生局部屈曲和整体屈曲时波纹腹板的刚度计算公式。

考虑到工字梁一般承受弯矩和剪力作用，波纹腹板可显著改善梁的抗剪屈曲性能，而弯矩则主要由翼缘承受。钢板翼缘工字梁因其平板翼缘没有足够的抗扭刚度容易发生整体失稳现象[8]。采用矩形、圆形和五边形等钢管混凝土翼缘来代替平板翼缘可以很好地提高工字梁抗扭刚度[9-11]。与平板翼缘工字梁相比，钢管翼缘梁惯性矩更大，截面抗扭刚度提升显著[12-13]。Sause[14]对钢管混凝土上翼缘平腹板工字型曲梁与平板翼缘工字形曲梁开展了对比试验，结果表明钢管混凝土翼缘梁扭转刚度较大，曲梁的整体稳定性显著提升。近年来，部分学者[15-17]将钢管混凝土翼缘和波纹板相结合，提出了一种钢管混凝土翼缘-波纹腹板工字梁构件，并对其抗弯和抗剪等性能进行试验和理论研究。结果表明，钢管翼缘可以有效增强钢梁的整体稳定性，同时波纹腹板可以大幅提高钢梁的抗剪承载力。

前期对波纹腹板以及钢管翼缘工字梁的研究主要集中在直梁构件中。随着曲梁在实际工程中的广泛应用，其受力性能的研究也逐渐被重视，如：Yossef[18]提出了平板翼缘波纹腹板曲梁剪切强度的预测公式，Gao等[19]研究了钢管混凝土翼缘平腹板曲梁的抗弯性能。考虑到钢管翼缘具有优良的抗扭性能而波纹腹板具有很好的抗剪性能，设计了钢管高强灌浆料翼缘-波纹腹板曲梁（CG-RGTF-CW），并通过试验测试和数值模拟方法对其抗剪性能进行研究。

1 试验概况

1.1 试件设计

为研究钢管高强灌浆料翼缘-波纹腹板曲梁（CG-RGTF-CW）受剪性能，参考《波纹腹板钢结构技术规程》（CECS 291—2011）[20]设计制作了4个缩尺试件（包括1根直梁和3根曲梁）用于开展曲梁的受剪承载力试验。试件设计过程中主要考虑以下几个因素：1）为防止曲梁在加载过程中侧翻而影响曲梁的受剪性能测试，曲梁弧度不宜设计过大，3个曲梁试件的弧度均取0.2 rad，对应曲率半径R=11.25 m。2）钢管内填充高强灌浆料以避免钢管翼缘在受集中荷载时出现局部屈曲。由于钢管翼缘尺寸限制，内部没有填充混凝土而是代替以高强灌浆料，主要是考虑混凝土骨料对填充质量的影响。3）考虑到梁横截面为单轴对称截面，中和轴上移，为避免下翼缘过早屈服适当加大下翼缘厚度。最终设计加工的4个试件上翼缘尺寸为bf×hu×tf=160 mm×60 mm×2.5 mm，下翼缘尺寸bf×tf=160 mm×12 mm，腹板厚度tw为2 mm，腹板高度hw为708 mm，跨度a为2 160 mm。所有试件详细尺寸如表1所示，其中ST-G1为直梁，CT-G1、CT-G2以及CT-G3为曲梁。试件正视图和俯视图如图1(a)所示，图1(b)为横截面示意图，图1(c)为波纹示意图，直梁和曲梁的波纹腹板均设计为直腹板。在曲梁的波纹腹板与翼缘焊接过程中，将直腹板弯曲成曲腹板。图1（c）中b为波纹子平板宽度，d为波纹子斜板投影长度，c为波纹子斜板宽度，α为波纹倾角，hr为波纹深度。曲梁钢管翼缘使用自动拉弧机进行弯曲加工，钢管翼缘、波纹腹板、门式加载板和端板采用焊缝连接，钢管内部填充普通型高强无收缩灌浆料。

表1 试件几何尺寸Table 1 Geometric dimensions of specimens

1.2 材性试验

钢材拉伸试件按照《金属材料拉伸试验第1部分：室温试验方法》（GB/T228.1—2010）[21]标准设计加工。拉伸试件分别在波纹腹板、钢管上翼缘以及下翼缘取样，每个位置取3个。材性试验所得屈服强度fy、极限抗拉强度fu、断裂后伸长率e和弹性模量Es平均值如表2所示。以《普通混凝土力学性能试验方法标准》（GB/T50081—2002）[22]为依据制作3个边长为150 mm的高强灌浆料立方体标准试块，用于测试钢管混凝土的立方体抗压强度。养护28 d后测得高强灌浆料立方体抗压强度平均值为69 MPa。

表2 钢材材料属性Table 2 Mechanical properties of steels

1.3 试验方法

试验在荷载量程为1 000 kN的四立柱压力试验机上进行，加载方案如图2~3所示。试验加载过程中约束曲梁两侧端板的侧向位移，曲梁两侧底部采用简支支座支撑。作动器下方设置刀铰装置以实现梁平面内自由转动且不发生平面外侧向翻转，如图3所示。试验机进行校正清零后在梁试件跨中位置施加集中荷载。加载分为预加载和正式加载两部分。首先预加载至0.2Pu（Pu为有限元模型预估的极限荷载），而后卸载并正式加载。正式加载过程首先采用位移控制加载至0.65Pu后，逐渐减缓加载速度直至腹板屈曲充分发展后终止试验。

图2 加载装置Fig. 2 Test loading device

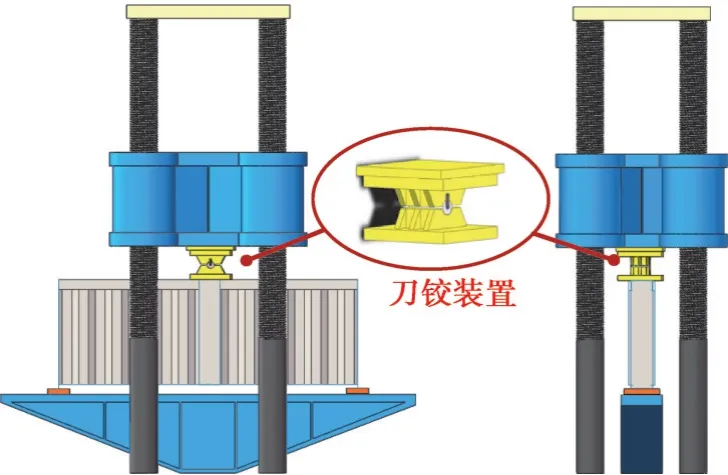
图3 加载示意图Fig. 3 Test loading diagram

1.4 初始缺陷测量

考虑到波纹腹板的几何初始缺陷对CG-RGTF-CW的抗剪性能的影响，在有限元模型中需要引入几何初始缺陷。波纹腹板的几何初始缺陷主要是腹板的平面外变形，如图4(a)所示。使用激光水平仪辅助梁调平以保证梁水平放置。借助铅垂线和水平尺测量翼缘至腹板间每块波纹子板的水平距离，将测得的值减去翼缘外伸长度便为腹板初始变形值。图4(b)为测量的不同试件腹板的初始缺陷值，3个试件波纹腹板的面外变形基本在2 mm之内。

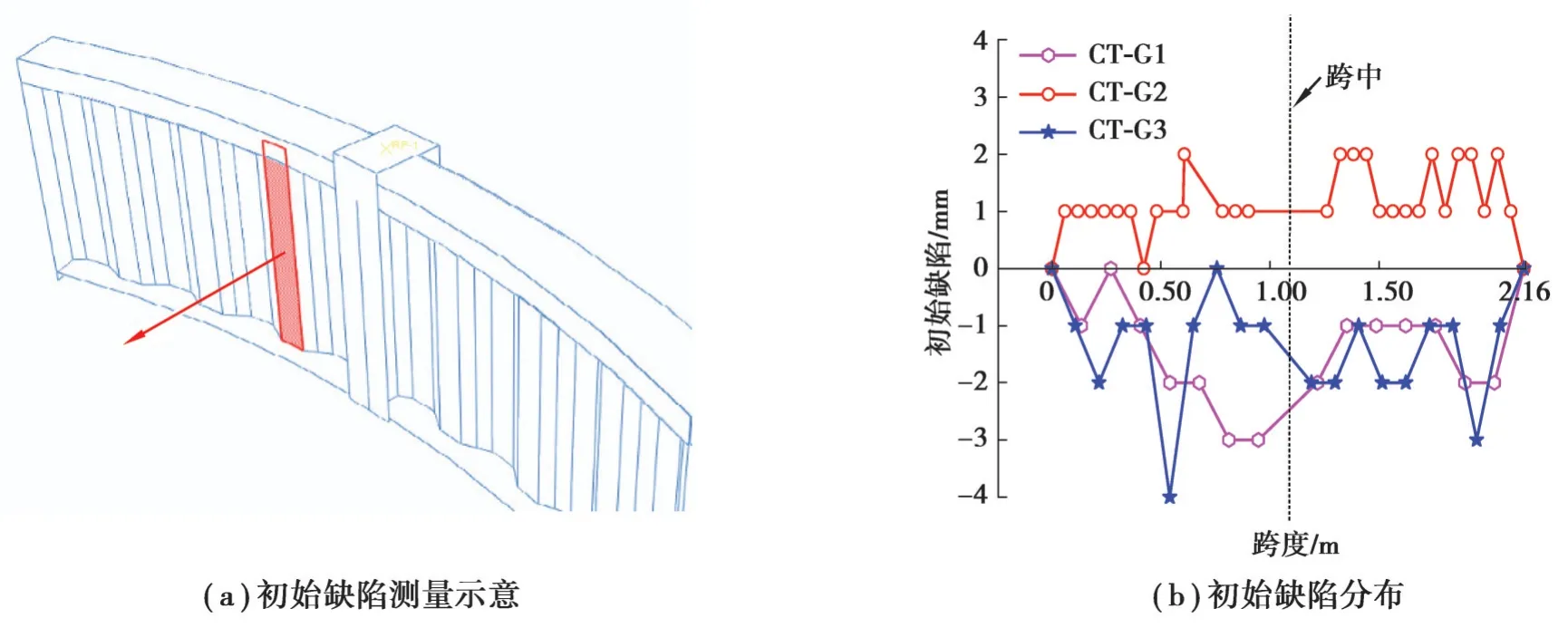
图4 试件的初始缺陷Fig. 4 Initial geometric imperfections of specimens

1.5 测点布置

CG-RGTF-CW受剪承载力试验中，采用三轴应变花监测波纹腹板失效过程的应变发展。试验准备阶段利用有限元模型模拟试件可能出现剪切屈曲的位置。在可能失效的位置布置一定数量的应变花用以监测腹板的应变。在腹板两侧对称位置布置位移计用于监测腹板面外位移，基于测得的位移值判断腹板的屈曲模式。在梁的跨中下翼缘两侧竖向对称位置布置2个位移计，两者测得的位移平均值做为试件的弯曲挠度。图5为不同试件的应变花和位移计的测点布置示意图，其中LVDT代表高精度电阻式位移计，数字1~54代表静态应变数据采集仪的采集通道。

图5 试件测量布置Fig. 5 Arrangement of strain rosettes and LVDTs

2 试验结果分析

2.1 失效模式

为准确描述CG-RGTF-CW试件的失效模式，分别采用白色和红色线条对波纹腹板屈曲位置和应变数据发生突变的位置进行突出标记，并对波纹子板自试件端板至跨中依次编号，如图6所示。图6(a)中白色线条标记了直梁试件ST-G1达到极限承载力时波纹腹板的屈曲位置，即3~5号波纹子板。屈曲位于单个波纹子板范围内，表明腹板发生了局部剪切屈曲。曲梁试件CT-G1在达到极限承载力时其失效模式如图6(b)所示，屈曲分别位于在6号和7号子板范围内，其失效模式与直梁试件ST-G1类似，表现为局部剪切屈曲。试件STG1和CT-G1均发生腹板的局部剪切屈曲主要原因是2个试件的波纹子板宽厚比较大，剪切屈曲的扩展能够被限制在较大宽度的子板区域内。图6(c)显示了曲梁试件CT-G2的失效模式，在1~6号波纹子板范围内形成了1个近似45°的跨越多个子板的屈曲范围，呈现出整体剪切屈曲特征。图6(c)同时发现试件的整体剪切屈曲出现在靠近下翼缘的区域。这是由于钢管上翼缘对波纹腹板的面外转动约束作用较强，腹板靠近上翼缘的屈曲发生时间滞后于腹板靠近下翼缘的屈曲，故腹板的屈曲位置下移。曲梁试件CT-G3失效模式如图6(d)所示。试件CT-G3达到极限承载力时，分别在1~3号波纹子板和4号波纹子板呈现出整体屈曲特征和局部屈曲特征，失效模式为耦合剪切屈曲。与试件GT-G2相比，试件CT-G3沿梁的高度方向呈现出更大的屈曲范围，原因是试件CT-G3因具有更小的波纹倾角（α=20°），腹板平面外弯曲刚度降低，从而增大了波纹腹板的屈曲范围，该现象与Yossef[18]的研究结果一致。

图6 失效模式Fig. 6 Failure modes

综上所述，不同波纹腹板形状和尺寸的CG-RGTF-CW试件在剪切载荷作用下呈现出不同的失效模式，较稠密的波纹腹板曲梁易发生腹板的整体剪切屈曲，而较稀疏的波纹腹板曲梁易发生局部剪切屈曲。在曲率较小时，曲梁和直梁的波纹腹板失效模式基本一致，曲率对失效模式影响不明显。

2.2 荷载-位移曲线

试件的荷载-位移曲线如图7所示。所有试件的荷载-位移曲线均呈现出线性增长至峰值载荷随后突然下降的趋势。试件CT-G1、CT-G2、CT-G3和ST-G1的波纹腹板屈曲失效时对应的跨中竖向位移分别为3.87、4.76、3.53、4.29 mm，均小于中国钢结构设计标准中构件作为主梁时的挠度容许值l/400=5.4 mm[23]。对比4组曲线发现，曲梁试件CT-G1和直梁试件ST-G1的刚度基本保持一致，表明曲率较小时对试件刚度影响较小。同时可以发现试件CT-G1和ST-G1的刚度略低于试件CT-G2和CT-G3，这是因为前二者较大的波纹倾角降低了其竖向刚度。Yossef[18]在研究中指出增大波纹倾斜角度超过一定范围时会降低梁的刚度，试验结果与该研究结论相吻合。

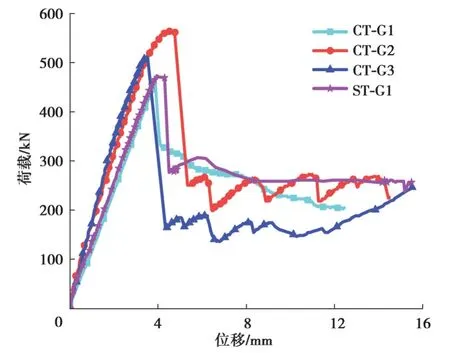
图7 跨中荷载-位移曲线Fig. 7 Load-displacement curves at mid span

试件CT-G1、CT-G2、CT-G3和ST-G1分别加载至458、564、512、473 kN时腹板发生屈曲，随后波纹腹板梁的荷载分别下降了峰值荷载的23%、55%、68%和41%。图7同样表明，所以试件的荷载达到极值点后均出现有大幅降低，表现出典型的回跳现象，属于不稳定分岔屈曲。对比直梁试件ST-G1与曲梁试件CT-G1的荷载-位移曲线发现，曲梁的曲率较小时曲率对承载力影响较小，两者的极限荷载接近。

2.3 荷载-应变曲线

波纹腹板的屈曲失效过程也可以通过布置的应变花监测的测点位置应变发展过程进行分析。将应变花所测的3个方向的线应变带入式（1）得到测点的主应变，将主应变带入式（2）得到等效应变。

图8~11为试件的荷载-等效应变曲线，其中(a)图为应变突变区域的荷载-等效应变曲线，(b)图为应变未突变区域的荷载-等效应变曲线。所有试件的荷载-等效应变曲线表明，加载过程中波纹腹板上的应变发展可以分为两个阶段：1）加载初期至荷载达到极值点前，应变随荷载呈线性增加；2）荷载达到极值点后，部分区域因屈曲引起应变值发生突变。应变未突变位置钢材仍处于弹性阶段，随着荷载的下降腹板表现为弹性恢复。将图8～11的(a)图中显示出应变值突变的应变花位置在图6中用红色方框标出。发现应变突变位置均处在屈曲范围内，可辅助验证试件的失效模式。

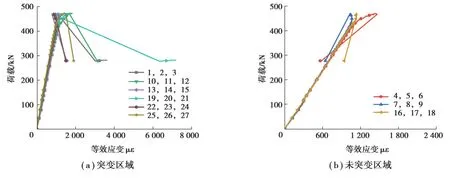
图8 ST-G1荷载-等效应变曲线Fig. 8 Load-equivalent strain curves for specimen ST-G1

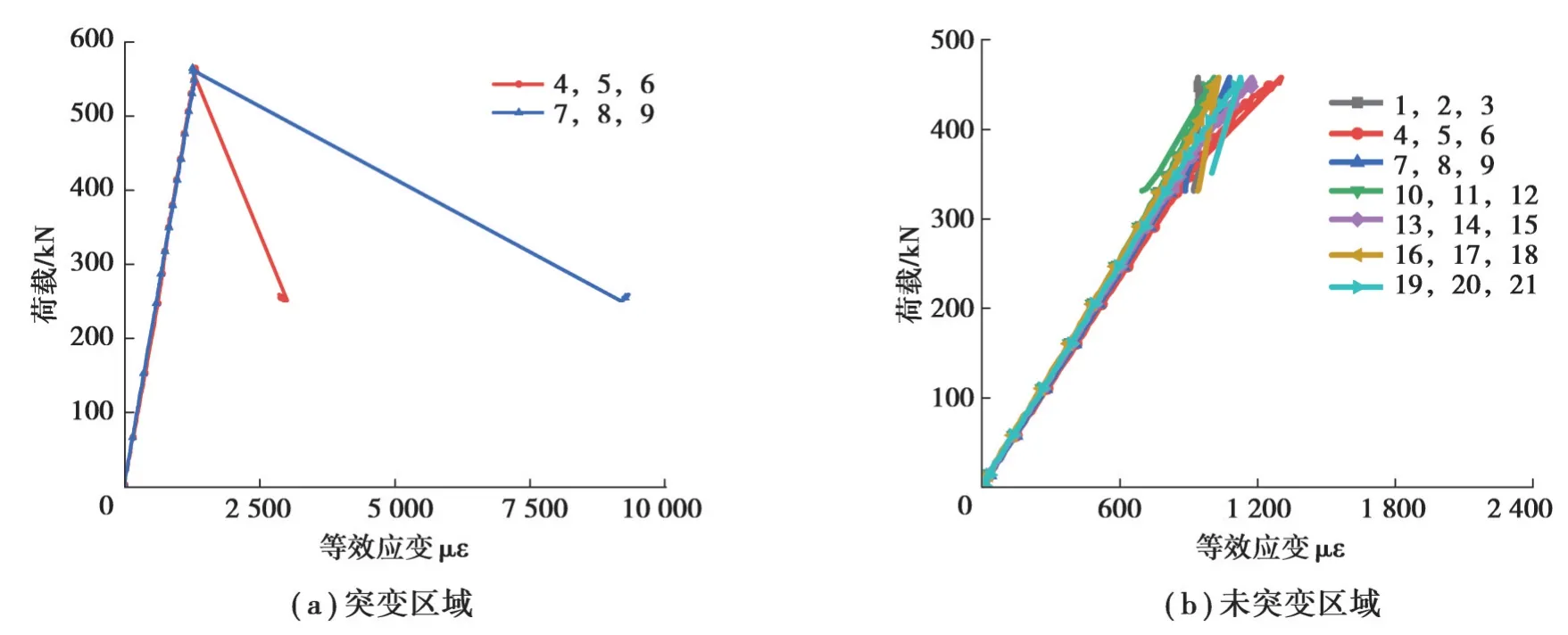
图9 CT-G1荷载-等效应变曲线Fig. 9 Load-equivalent strain curves for specimen CT-G1

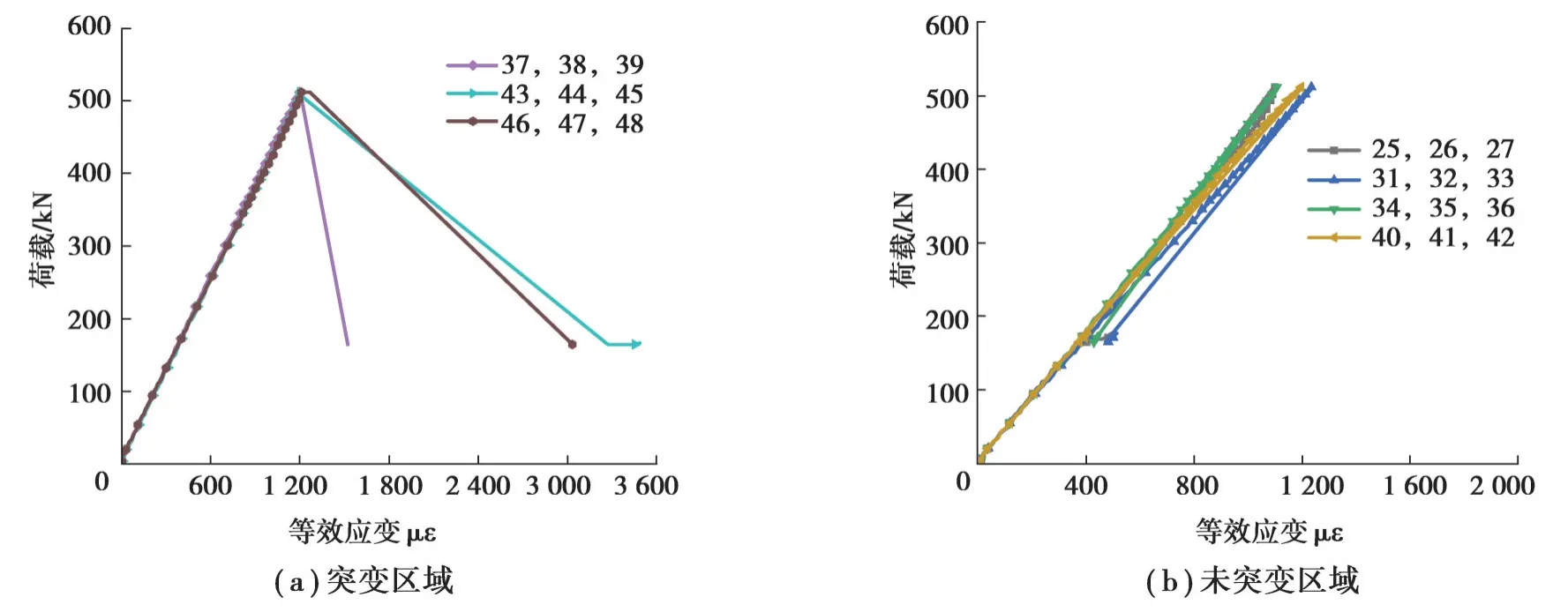
图11 CT-G3荷载-等效应变曲线Fig. 11 Load-equivalent strain curves for specimen CT-G3

2.4 荷载-侧向位移曲线

为便于描述腹板侧向位移的发展，在试件失效模式图（如图6所示）用黄色圆点标记位移计布置位置。图12(a)为直梁试件ST-G1的荷载-侧向位移曲线。在达到峰值荷载474 kN时，2号及3号位移计测量值发生突变，其余测量值没有显著变化，这与实验中观察到的现象一致，即腹板屈曲只发生在3～5号波纹子板。从图12(b)中可见，曲梁试件CT-G1达到峰值荷载时，位移计的测量值均未出现突变。随着荷载下降至330 kN，3号位移计测量值开始突变。荷载进一步下降至310 kN后，同样的现象出现在2号位移计中。位移计测量值的变化情况与试验中所观察的现象一致，曲梁试件CT-G1的屈曲从6、7号子板靠近跨中下翼缘处开始，而后沿45°方向向上依次延伸至5号子板及3号子板。曲梁试件CT-G2的荷载-侧向位移曲线如图12(c)所示。峰值荷载后，1~3号位移计因所在子板屈曲引起侧向位移值突变。7号及8号位移计均在试件未破坏的一侧，在荷载下降过程中测量值也出现增大，这是由于曲梁试件发生平面外倾斜所导致的。曲梁试件CT-G3的荷载-侧向位移曲线见图12(d)。5号及6号位移计测量值因腹板屈曲产生突变。4号位移计不在屈曲范围但监测到相对较小的侧向位移突变，这可能是由于1~4号子板较大的屈曲变形影响相邻子板所导致。

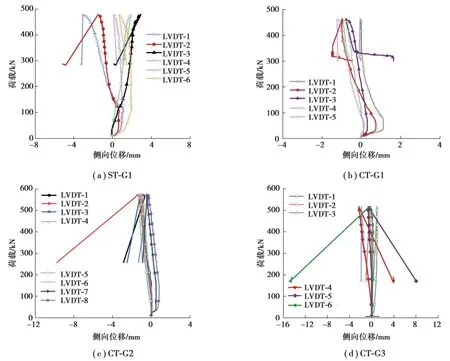
图12 腹板荷载-侧向位移曲线Fig. 12 Load-lateral displacement curves of corrugated web

3 有限元分析

3.1 有限元模型

在有限元模型中，采用8节点线性缩减积分三维实体单元（C3D8R）模拟上翼缘钢管内的高强灌浆料，钢管和钢板采用4节点缩减积分曲壳单元（S4R）模拟。模型采用结构式网络划分技术。经过收敛性试算，网格尺寸取翼缘宽度1/5可以在满足计算结果收敛的要求下提高计算效率。在相互作用方面，假定钢管与混凝土表面无相对滑移，并采用“Tie”约束将矩形钢管与混凝土进行绑定。在门式垫板中间设置参考点与垫板上表面进行耦合。边界约束及加载情况如图13所示。钢材采用Han等[24]提出的简化五阶段本构关系，其中弹性模量、屈服强度和极限强度采用实测拉伸试验数据。高强灌浆料的材料属性使用Han等[24]提出的等效应力-应变关系进行定义。将Buckle分析中第一阶屈曲模态作为初始几何缺陷引入Risk非线性静力分析中，缺陷取试验测得最大值。

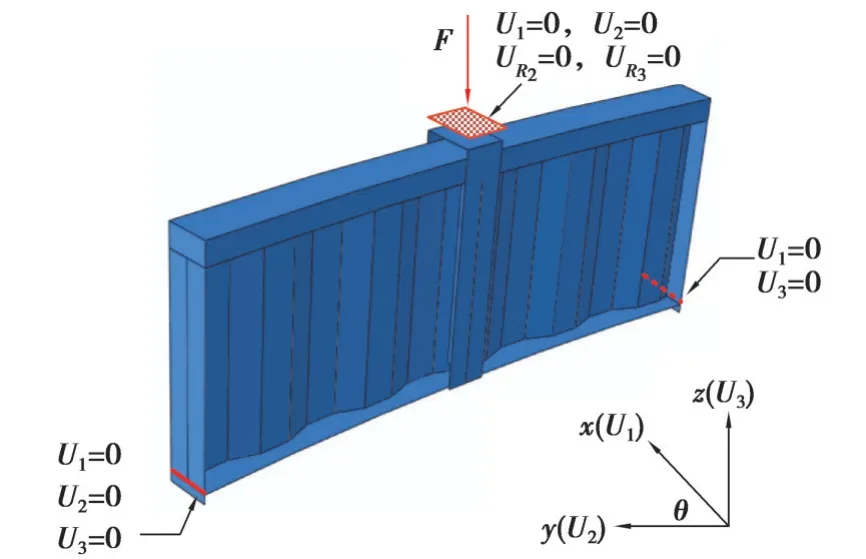
图13 边界约束Fig. 13 Boundary conditions

3.2 结果分析

图14为4个试件在极限荷载时的破坏模式对比图。从图14(a)和图14(b)可知，试件ST-G1和CT-G1的屈曲都发生在单个子板，均为局部剪切屈曲。试件CT-G2子板较窄，屈曲横跨多个子板为整体剪切屈曲，如图14(c)所示。从图14(d)可见，波纹腹板发生耦合剪切屈曲。综上，4个试件的有限元失效模式均与试验结果相同。试验与有限元模型所得荷载-位移曲线对比如图15所示。试验试件承载力和刚度与有限元模拟结果接近。表3中列出了详细的承载力对比，结果表明有限元结果误差均在10%以内，验证了有限元模型的精确性。

图14 试验与FE破坏模式对比Fig. 14 Comparison of failure modes between test and FE for four specimens

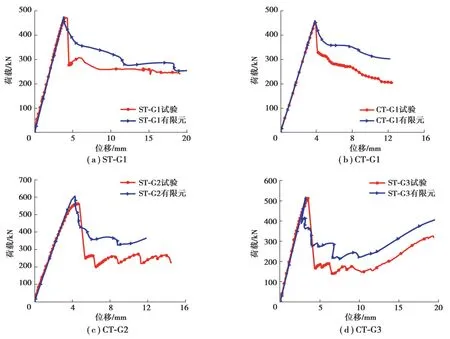
图15 试验与FE荷载位移曲线对比Fig. 15 Comparison of load-displacement curves between the test and FE results

表3 试验与FE极限荷载对比Table 3 Comparison of the ultimate capacity between FE and test results

4 参数分析

为进一步研究不同参数对CG-RGTF-CW抗剪性能的影响，采用提出的有限元模型进行了参数分析。根据文献[25]的参数范围建议，分析了曲率，腹板高厚比hw/tw，波纹子平板宽b，波纹倾角α，波纹深度hr和腹板约束条件等参数对CG-RGTF-CW抗剪性能的影响。参数分析中采用的CG-RGTF-CW模型基本尺寸如表4所示。

表4 模型基本几何尺寸Table 4 Basic geometric dimensions of models

4.1 曲率（Z）的影响

曲率参数Z反应曲梁的弯曲程度，由式（3）计算得到[18]，式中a为跨度、R是曲率半径、tw为腹板厚度、ν是泊松比。参数分析中，模型的Z值分别取0、200、400、600、800、899。

随着梁曲率的增加，失效模式（10倍放大图）及荷载-位移曲线出现显著变化，分别如图16~17所示。当曲率参数Z从0增加到200时，腹板发生耦合剪切屈曲，梁的刚度有所降低，承载力下降约1.5%。考虑曲梁扭转变形影响，腹板发生屈曲破坏时腹板上剪力分量为F×cosφ=0.98F，如图18所示。可近似认为该峰值荷载即为腹板屈曲失效的承载力。此时曲率较小，对腹板剪切屈曲强度影响不大。

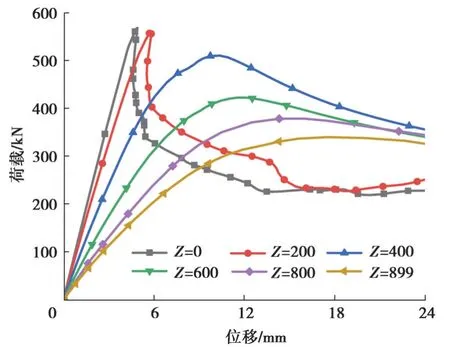
图17 不同Z模型的荷载-位移曲线Fig. 17 Load-displacement curves with different curvatures

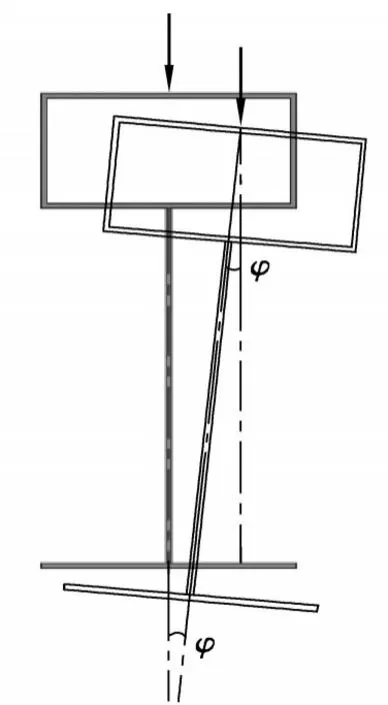
图18 模型受载偏转示意图Fig.18 Diagram of model deflection

随着曲率进一步增大，梁弹性阶段刚度逐渐降低，承载力大幅下降，构件失效模式由腹板屈曲向整体弯扭失效转变。与小曲率梁(Z<200)不同，在达到峰值荷载时，曲率较大的梁的钢管翼缘进入屈服。这意味着上翼缘承担的荷载增大，钢管高强灌浆料翼缘抗弯扭性能得以发挥。上翼缘弯曲产生的附加扭矩，使模型发生整体弯扭变形失效，腹板并未屈曲。

4.2 波纹子平板宽度（b）的影响

通过改变波纹子平板宽度(b)以研究子板宽高比(b/hw)对CG-RCFTF-CW抗剪性能的影响。b分别取30、50、80、100、130、230 mm。hw保持不变为700 mm，b/hw分别为0.04、0.07、0.11、0.14、0.18、0.32。第一阶屈曲模态如图19所示。从图19中可知，随着b增加，b/hw增大，屈曲模式由耦合剪切屈曲向局部剪切屈曲转变。荷载-位移曲线如图20所示，随着b/hw增大，试件承载力有所降低，试件刚度变化不显著。当b/hw＜0.14时腹板发生耦合剪切屈曲。此时b/hw对梁的极限承载力影响不大。当b/hw＞0.18时，腹板发生局部剪切屈曲，极限承载力有较大幅度下降。由此可见，在波纹尺寸设计中，合理调整子板水平板宽，降低宽高比b/hw，可改善CG-RCFTF-CW的承载力，充分发挥腹板材料性能。

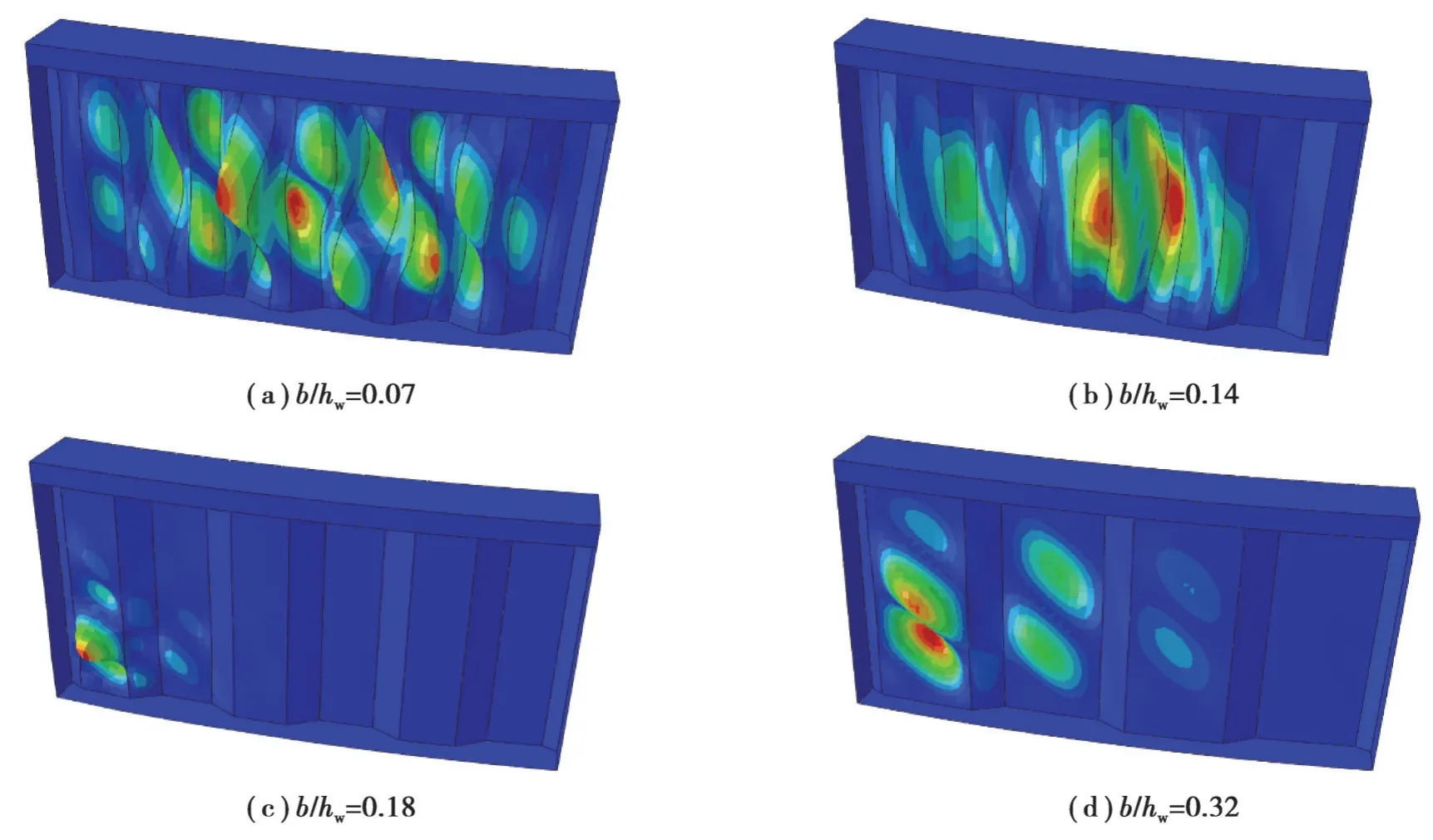
图19 不同b模型的屈曲模态Fig. 19 Buckling modes with different corrugation lengths

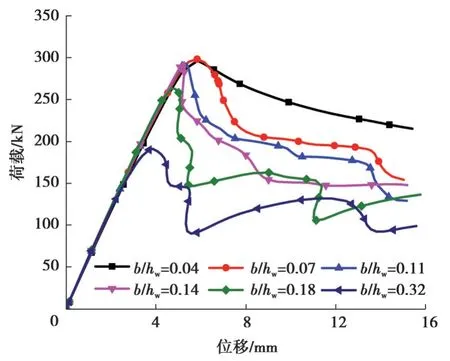
图20 不同b模型的荷载-位移曲线Fig. 20 Load-displacement curves with different corrugation lengths

4.3 波纹倾角（α）的影响

波纹倾角(α)分别取23°、30°、45°、50°。荷载-位移曲线和第一阶屈曲模态分别如图21~22所示。随着波纹倾角增加，承载力逐渐提高，刚度呈略微下降趋势。当波纹倾角小于30°时，腹板发生耦合剪切屈曲。保持子斜板水平投影长度(d)不变，增大波纹倾角同时会增大子斜板宽度(c)。当α为45°和50°时，较大的子斜板宽度会导致腹板发生局部剪切屈曲。因局部屈曲不涉及相邻子板，所以α对局部剪切屈曲强度影响不大。此时增加α承载力不再显著变化。

图21 不同α模型的荷载-位移曲线Fig. 21 Load-displacement curves with different corrugation angles

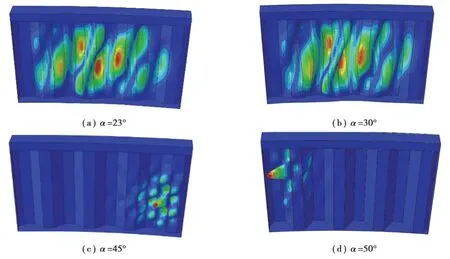
图22 不同α模型的屈曲模态Fig. 22 Buckling modes with different corrugation angles

4.4 腹板高厚比（hw/tw）的影响

腹板高度(hw=700 mm)不变，腹板厚度(tw)分别取1、1.5、2、2.5、3、3.5、4 mm，hw/tw分别为700、466、350、280、233、200、175。如图23所示，随着tw值增大，梁的刚度和承载力均增大。对于280

图23 不同hw/tw模型的荷载-位移曲线Fig. 23 Load-displacement curves with different hw/tw ratios

图24 不同hw/tw模型的屈曲模态Fig. 24 Buckling modes with different hw/tw ratios

4.5 波纹深度（hr）的影响

腹板厚度(tw=2 mm)保持不变，hr分别取23.16、40.52、57.85、69.37、127.27 mm，相应的hr/tw为11.58、20.26、28.92、34.68、63.63。当hr/tw＜20.26时，腹板发生耦合剪切屈曲。保持波纹倾角α不变，增大hr的同时会引起波纹子斜板宽度c的增大。当hr/tw超过28.92时，因子斜板宽度较大，腹板发生局部剪切屈曲，如图25所示。

图25 不同hr模型的屈曲模态Fig. 25 Buckling modes with different corrugation depths

图26中的荷载-位移曲线表明，腹板发生耦合剪切屈曲时极限承载力较大。腹板发生局部剪切屈曲时，承载力随hr/tw增加而逐渐减小。

图26 不同hr模型的荷载-位移曲线Fig. 26 Load-displacement curves with different corrugation depths

4.6 翼缘与腹板约束条件的影响

波纹腹板剪切屈曲强度受边界约束条件影响，为研究钢管高强灌浆料翼缘对波纹腹板抗剪屈曲性能影响，分别对简支(simple juncture, S)和固支(fixed juncture, F)下的波纹腹板进行弹性屈曲分析[26]。腹板临界剪切屈曲强度如表5所示，表中τcr,S为简支条件下的剪切屈曲强度，τcr,F为固支条件下的剪切屈曲强度。从表5中可知，固支边界约束下波纹腹板的临界剪切屈曲强度稍高，CG-RCFTF-CW临界屈曲荷载比腹板在固支约束条件下的临界屈曲荷载高，原因有两方面：一是由于钢管翼缘对波纹腹板约束较强；二是钢管高强灌浆料翼缘承担了部分剪力。当波纹腹板厚度较小时，翼缘与腹板的约束对腹板临界剪切屈曲强度影响更为显著。降低波纹腹板高厚比也可以提高腹板抗剪性能。曲率大小对波纹腹板抗剪屈曲性能影响较小。钢管高强灌浆料翼缘对腹板的约束作用较强且能承担部分剪力，对波纹腹板抗剪屈曲性能具有显著提升作用。

表5 不同约束临界剪切屈曲强度Table 5 Critical shear stress of the corrugated web with different constraints

5 结 论

对钢管高强灌浆料翼缘-波纹腹板新型曲梁和直梁的抗剪切性能进行了试验和有限元分析，基于研究结果可得出以下结论：

1）钢管高强灌浆料翼缘-波纹腹板曲梁（CG-RCFTF-CW）的波纹疏密程度不同会导致梁的失效模式发生改变。波纹较稠密易发生腹板整体屈曲，较稀疏易发生腹板局部屈曲。

2）曲率较小时，曲梁与直梁承载力基本一致。随着曲率参数Z增大，承载力下降，曲梁破坏模式由腹板屈曲向整体弯扭屈曲转变。

3）增大腹板厚度tw，降低腹板高厚比(hw/tw)，可显著提高CG-RCFTF-CW的承载力。波纹倾角α和波纹深度hr的不同会造成腹板屈曲形式的不同。

4）钢管高强灌浆料翼缘对腹板约束较强且能承担部分剪力，在梁总体高度不变的情况下，钢管翼缘由于具有一定高度可降低腹板高厚比，从而提高波纹腹板抗剪屈曲性能。