考虑半刚性连接的输电塔结构离散优化设计方法

李正良，彭思思，王涛,2

（1. 重庆大学 土木工程学院，重庆 400045;2.哈尔滨工业大学 交通科学与工程学院，哈尔滨150090）

随着国家输电电网建设步伐的加快以及电网工程向着特高压不断升级[1]，输电线路的要求日益提高，不仅要考虑结构的安全性，更要考虑其经济性。输电塔作为输电线路的重要组成部分，其用钢量大、工程造价成本占比高，对其进行结构优化设计具有重要现实意义和经济效益。

1971年Beck等[2]叙述了计算机对输电线路设计产生重要影响，此后，基于计算机的输电线路优化设计得到了极大拓展，国内外学者将不同优化方法应用于输电塔优化设计领域，对输电塔塔身、塔腿、斜材等的截面、形状、拓扑以及组合优化设计展开大量研究[3-11]，相关研究成果颇丰：Taniwaki等[3]探究了包含218根杆件的输电塔整塔在静载和地震荷载作用下的组合优化问题；Rajeev[4]、王藏柱[5]、郭惠勇[6-7]等对除塔头以外的输电塔塔身进行优化设计；张卓群等[8]研究了输电塔塔身局部截面、形状、拓扑和组合优化问题；邓洪洲[9]等提出了针对输电塔交叉斜材的拓扑优化方案；崔磊[10]、郭惠勇[11]等采用不同优化算法实现输电塔下部塔腿的拓扑优化设计。在输电塔结构优化设计中，通常假定杆件之间的连接为铰接进行计算，在实际工程中，由于输电塔节点板连接处螺栓群和节点板共同受力并产生剪切变形，节点的受力特征往往介于二者之间，即半刚性连接。与铰接的零刚度以及刚接的无穷大刚度不同，输电塔的半刚性连接节点具有一定转动刚度，因此在受力变形过程中能够传递部分弯矩，且产生一定相对转角，这种半刚性力学特征会对输电塔整体受力性能产生不可忽视的影响。

为考虑连接节点的半刚性特性对输电塔结构受力-变形的影响，王朋等[12]探究了角钢输电塔螺栓滑移性能及其对输电塔的受力-变形特征的影响；Jiang等[13]针对不同节点的连接刚度，总结了构造节点对输电塔动静态特征的影响规律；安利强等[14]采用一种刚度可调的半刚性连接单元模拟特高压钢管塔节点连接，分析了半刚性节点对钢管塔静力特征的影响；钱程等[15]提出考虑节点半刚性连接对输电塔自振特征和风致响应的影响，表明考虑半刚性连接的输电塔模型更为合理。

综上所述，输电塔结构中不宜简单忽略半刚性节点的影响，但目前考虑半刚性连接输电塔的相关研究仍较少，尤其考虑半刚性连接的输电塔结构优化设计现有文献更少。笔者建立了考虑半刚性连接的输电塔有限元模型，提出考虑半刚性连接的输电塔优化数学模型，进而基于粒子群优化(PSO)算法发展了一种考虑半刚性连接的输电塔离散优化设计方法。

1 考虑半刚性连接的输电塔有限元模型

以沿海地区某220 kV角钢输电塔为例，其结构如图1所示。该塔高60.4 m，根开10.56 m，水平档距350m，垂直档距为550 m。

图1 输电塔K形节点构造示意图Fig. 1 K-joint of transmission tower

笔者采用ANSYS软件建立输电塔有限元模型，其中输电塔杆件采用BEAM单元进行建模，杆件采用理想弹塑性本构关系模型，钢材密度为7 850 kg/m3，弹性模量为2.06×105MPa，屈服强度设为345 MPa。输电塔所受荷载包括永久荷载以及可变荷载，其中永久荷载主要为输电塔塔身构件的自重荷载以及导线、地线的重力荷载，施加在输电塔有限元模型的可变荷载主要包括塔身的风荷载、导地线传至塔身的风荷载和金具绝缘子的风荷载。

为考虑半刚性连接对输电塔结构的影响，通过输电塔半刚性节点的弯矩-转角(M-θ)关系描述其力学性能，采用参考文献[16-17]中提供的角钢输电塔半刚性节点弯矩-转角(M-θ)曲线，如图2所示。为简化计算，有限元模型中各半刚性节点在X、Y、Z方向上的空间转动均采用同一条M-θ曲线[18]。

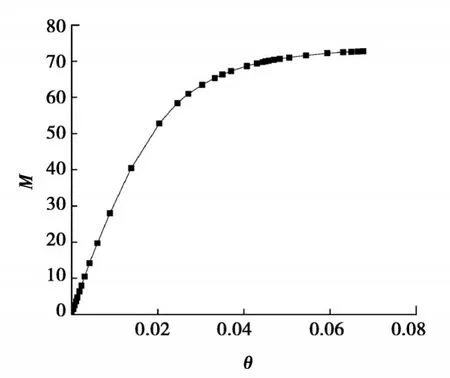
图2 半刚性节点的M-θ曲线Fig. 2 The M-θ curve of semi-rigid joints

在考虑半刚性连接的输电塔有限元模型中，将图1 所示的输电塔塔身部分主材与交叉斜材的连接节点视为半刚性连接，其连接处简化模型如图3所示，使用COMBIN39弹簧单元模拟半刚性节点的力学行为，可通过定义实常数输入节点的弯矩-转角曲线。

图3 K形节点有限元模型Fig. 3 The finite elements model of K-joint

2 考虑半刚性连接的输电塔优化数学模型

对考虑半刚性连接的输电塔进行离散优化设计，其目的是在满足各项要求前提下，实现结构轻量化、经济化设计。在对输电塔结构进行优化设计前，首先建立相应的优化设计数学模型。

2.1 优化设计变量

优化设计变量的选取即确定自变量及其取值范围。在考虑半刚性连接的输电塔优化问题中，对输电塔除塔头以外塔体部分的主材杆件进行截面优化设计，故优化设计变量为输电塔塔身主材构件截面尺寸，其取值是不连续的，可以根据不同主材截面所采用的型钢种类，将其设为多个离散设计变量。每个设计变量的取值需满足

式中：n为设计变量个数；优化设计变量X={x1,x2,…,xn}；Si为第i个离散变量的取值集合，一般来源于常用的输电塔角钢型号表。

2.2 优化目标函数

优化设计目标函数是以设计变量为自变量的函数表达式，函数值应与自变量的取值对应。对于输电塔塔架结构，其工程造价主要来源于结构的钢材用量，故在满足结构安全性的前提下，造价成本成为了设计人员主要的考虑因素。在考虑半刚性连接的输电塔离散优化设计中，为降低成本、节省材料，以结构杆件的总质量作为优化目标函数，即

式中：W表示输电塔杆件的总质量；n为设计变量总数，即优化中主材杆件数目；ρi为第i根杆件的材料密度，统一取钢材密度ρ=7 850 kg/m3；Ai为第i根杆件的横截面面积；li为第i根杆件的计算长度。

2.3 约束条件

为了防止输电塔塔身主材构件发生强度破坏，保证结构的安全使用，荷载作用下的杆件应力绝对值不应大于材料的容许应力值，故杆件应满足下列应力约束条件

式中：σi表示第i根杆件的应力；Ni表示第i根杆件的轴力；Ai为第i根杆件的横截面面积；φi为第i根杆件的稳定系数；[σ]i为第i根为杆件的容许应力值，可通过调节容许应力值使设计的半刚性连接输电塔结构具有一定安全裕度。

同时，为保证结构正常使用，在荷载作用下输电塔整体结构应具有足够刚度，限制结构的最大位移绝对值不大于给定的位移上限值，故变形约束条件为

式中：umax为荷载作用下考虑半刚性连接输电塔结构产生的最大位移；[u]为给定的容许位移值。

2.4 优化数学模型

对于考虑半刚性连接的输电塔离散优化设计问题，其数学模型可写为如下形式

式(5)所示的输电塔经济性优化设计数学模型中给出了设计变量约束条件和状态变量约束条件，得到最优设计结果既能满足所有的约束条件又能得到最小的目标函数值，实现结构的安全性指标，同时保障了经济性。

3 半刚性连接的输电塔离散优化设计方法

3.1 优化算法

在考虑半刚性连接的输电塔离散优化设计中，采用计算简单、易于实现的粒子群优化(particle swarm optimization，PSO)算法[19]进行寻优，通过MATLAB软件编写基于代理模型的离散优化设计算法程序，其中PSO算法参数设定如表1所示。

表1 PSO算法参数值Table 1 The parameter values of PSO algorithm

在式(5)所示的优化数学模型中，应力约束条件和变形约束条件是与设计变量相关的状态变量约束条件，对于该约束优化问题，需进一步采用罚函数法计算优化目标函数的适应度值。定义罚函数P(x,a)为

式中：系数a被称为惩罚系数，通常为一个很大的正数；h1(x)和h2(x)可分别如下计算

进而，PSO优化算法中适应度函数F(x)为

3.2 考虑半刚性连接的输电塔优化设计流程

对考虑半刚性连接的输电塔进行截面优化设计（如图4所示），即改变结构杆件的截面尺寸，寻找满足约束条件的最优截面面积，使构件的应力接近满应力状态，实现材料的充分利用。

图4 考虑半刚性连接的输电塔离散优化设计流程Fig. 4 Discrete optimization flowchart for transmission tower with semi-rigid joints

基于半刚性连接的输电塔离散优化设计方法的流程如图4所示，其具体步骤为：

1)建立基于半刚性连接的代理模型优化设计的数学优化模型，确定离散优化设计变量x、约束条件以及优化目标函数W；

2)获取输电塔连接节点的实际弯矩-转角曲线；其次在ANSYS软件中采用弹簧单元模拟半刚性连接节点的力学行为，建立考虑半刚性连接的输电塔有限元分析模型；然后设置输电塔有限元模型中单元属性、网格划分、接触单元、荷载大小、非线性分析等相关参数，计算输电塔的结构响应；

3)采用粒子群算法求解离散优化问题：初始化优化算法参数后，在设计空间中抽取一定数量的初始样点X0={x1,x2,…,xn}，通过有限元模型计算样本点对应的输电塔杆件的应力σ和结构的最大位移umax，并根据等式(8)计算优化算法中粒子的适应度函数，依据算法规则进行寻优，直至优化迭代次数达到给定的最大迭代次数，输出结构最优设计结果{xmin、Wmin}。

4 优化设计结果分析

在考虑半刚性连接的输电塔结构离散优化设计中，共涉及64根输电塔主材杆件，将主材截面尺寸按不同高度、不同区域分为16组，故离散优化设计变量的个数n=16，在优化过程中每根角钢有6种不同截面型号可供选择，其取值如表2所示。

表2 离散变量的尺寸集合Table 2 Allowable values for the discrete design variables

1)优化过程分析

采用基于罚函数法的PSO算法对半刚性连接的输电塔进行离散优化设计，其优化收敛曲线如图5所示。

图5 离散优化过程Fig. 5 The process of discrete optimization

图5中展示了优化的输电塔杆件总质量随PSO算法迭代次数的变化趋势，随着优化次数的增加，构件总质量逐渐下降并最终趋于一个稳定值，在前40代，优化算法在设计空间中不断探寻潜在最优解，收敛速度较快；在40代左右找到一个最优解，此后杆件总质量最小值不再发生变化。

2)优化前后杆件质量对比

依据方法对半刚性连接的输电塔主材进行离散优化设计，并对优化结果进行分析。优化设计前后杆件截面尺寸发生变化的情况如表3所示。

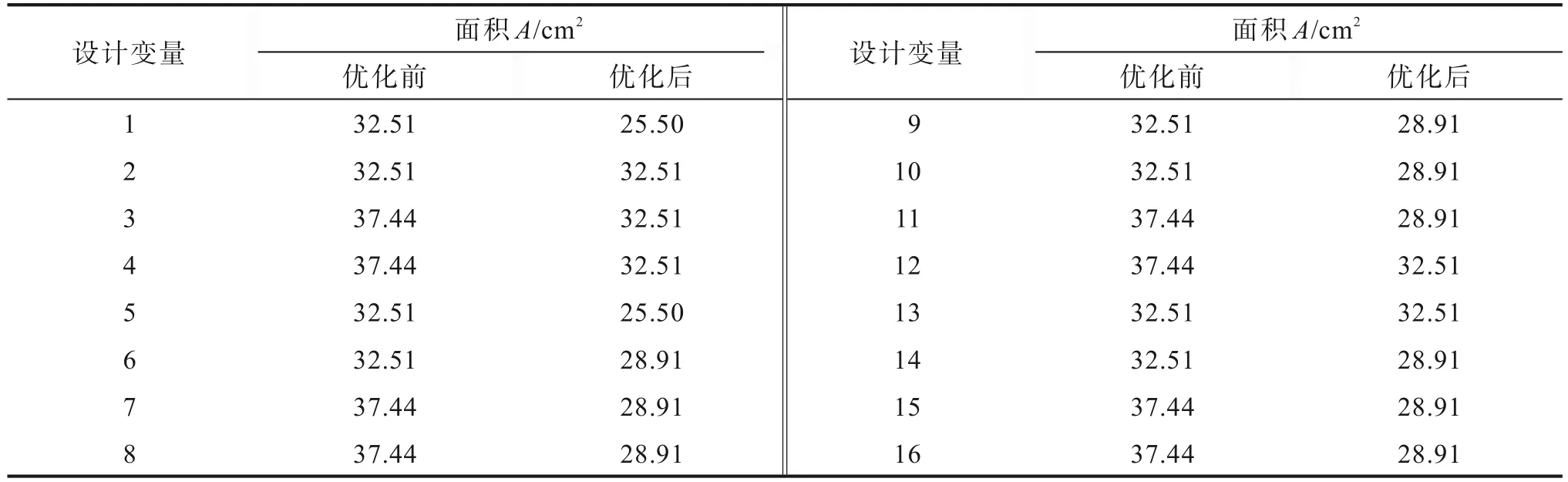
表3 优化前后截面面积对比Table 3 Comparison of section area before and after optimization

从表3可以观察到，在优化后各杆件的截面设计发生了显著变化，其截面面积有所下降，进一步比较优化目标函数结果，优化设计前后构件重量的对比情况见表4。

表4 优化前后总重量对比Table 4 Comparison of weight before and after optimization

由表4可知，对考虑半刚性连接的输电塔主材进行离散优化有效降低钢材的总质量，减少钢材消耗量，节约经济成本，该输电塔离散优化设计的优化效率ξ为

3)优化前后杆件应力、位移对比

对优化设计前后考虑半刚性连接的输电塔进行结构响应分析，输电塔主材杆件的应力以及输电塔结构的最大位移分别如表5和表6所示。

表6 优化前后杆件位移比较Table 6 Comparison of displacement before and after optimization

由表5可知，在离散优化设计后，输电塔主材的应力随着杆件横截面面积变化发生相应变化，与优化前对比，除杆件9、44、46的应力基本不变或略有减小，其他杆件的应力均在原基础上小幅上升，对杆件材料的利用效率更高；为保证结构具有一定的安全裕度，在应力约束条件中设置的应力容许值较小，故上述杆件应力变化幅度较小，且均未达到严格的满应力状态，在应用中设计者可根据实际要求做出相应调整。

此外，由表6可知，对输电塔主材截面尺寸进行优化设计后，由于绝大多数截面尺寸减小，输电塔整塔结构在X、Y、Z3个方向上的最大位移均有所上升，但影响较小，处于所给定的位移约束要求范围内。

5 结 论

对考虑半刚性连接的输电塔结构进行离散优化设计，主要结论如下：

1) 通过引入实际输电塔半刚性节点的弯矩-转角曲线，采用弹簧单元模拟半刚性节点的力学性能，建立考虑半刚性节点的输电塔有限元模型；

2) 建立了考虑半刚性连接的输电塔结构离散优化设计数学模型和方案，提出考虑半刚性连接的输电塔优化设计方法；

3) 对半刚性连接的输电塔结构进行离散优化设计，在满足结构应力及变形约束的条件下减少了13.39%的输电塔用钢量，提高材料利用率，有良好的工程经济效益。