基于互层岩体的非定常黏弹塑性蠕变模型及有限元分析

胡涛涛，康志斌，陈建勋，胡雄，王栋

（1. 长安大学 公路学院，西安 710064； 2. 中交第一公路勘察设计研究院有限公司，西安 710065）

岩体的蠕变效应是隧道工程、采矿工程及边坡工程发生时效变形乃至失稳破坏的重要原因之一[1-3]。对于软弱岩体及含有夹层破碎带的松散岩体，其蠕变现象尤为显著[4]；在高地应力状态下，即便是中等强度的岩体或存在节理发育的硬岩也存在一定程度的流变效应[5-6]；由此可见，岩体的蠕变现象在自然界是普遍存在的。岩体的蠕变特性对隧道及边坡结构的安全性和长期稳定性有重大影响，建立能够描述岩体全程蠕变特性的蠕变模型至关重要。然而，软硬互层岩体的蠕变特性更为复杂，其在相同的应力条件下软岩与硬岩具有不同的变形特性（软岩较硬岩更容易出现加速蠕变现象）[7]，为重大岩土体工程实践带来了严峻的挑战，这就需要对岩体蠕变模型展开进一步的研究。

针对岩体的蠕变特性，Griggs[8]最先对灰岩、页岩等软岩进行蠕变试验研究，发现当加载于软岩时的荷载达到破坏荷载的12.5%~80%，就会产生一定程度的蠕变现象；Fujii等[9]对花岗岩进行了三轴蠕变试验，得到了轴向应变、环向应变和体积应变等多种蠕变曲线，提出环向应变可以作为判断岩体损伤的重要指标。近年来，随着损伤断裂力学的等新理论的引入，岩体加速蠕变模型成为了岩体流变力学研究的热点。徐卫亚等[10]将非线性黏塑性体与五元件黏弹性模型串联建立了河海模型，充分反映了岩体的加速流变特性；王闫超等[11]以巴东组泥岩为研究对象，通过引入应变阈值的非线性牛顿体元件，建立了一个新的八元件非线性蠕变本构模型；张亮亮等[12]在经典元件模型的基础上引入非线性元件和蠕变损伤的方法，描述了岩体整个蠕变过程中的非线性蠕变特性；此外，大型数值仿真软件在工程实践中的应用越来越广泛，多被用来解决应力条件复杂的特殊岩土体问题，有学者将复杂的流变模型通过二次开发集成于有限元软件或有限差分软件中[13-15]，为数值研究提供了更为丰富的基础资料，对复杂地质条件的工程实践提供了指导作用。时至今日，国内外学者已经在岩石蠕变特性的理论研究及工程实践中取得重大成果[16-22]，但仍然存在一些不足：其一，大量的研究仍然聚焦于完整岩体蠕变特性的研究，对于软硬互层岩体蠕变特性的研究极少[23-24]；其二，岩体的非线性蠕变特性与岩体的应力状态和应力作用时间密切相关，而忽略了岩体的应变状态对加速蠕变特性的影响，其合理性有待商榷。

为此，笔者在Burgers模型的基础上提出了一种考虑应力、应变阈值的黏弹塑性蠕变模型，用以描述互层岩体的蠕变特性；并结合ABAQUS有限元软件的UMAT接口子程序完成了该数值程序的二次开发，根据文献[25-26]中的单轴压缩试验验证了该程序的正确性与有效性。

1 黏弹塑性流变模型

1.1 黏弹塑性流变模型的特性

完整岩体尤其是软弱岩体在给定的应力条件下具有时效变形的特性，即岩体的流变特性。具有流变特性的岩体的蠕变分为减速蠕变Ⅰ（ab）、稳态蠕变Ⅱ(bc）和加速蠕变Ⅲ(cd）3个阶段，如图1所示。丁秀丽等[7]表明软硬互层岩体的流变特性明显不同，软岩蠕变变形包括减速蠕变、稳态蠕变和加速蠕变3个阶段，符合黏弹塑性本构模型的蠕变特性；硬岩的蠕变变形仅存在减速蠕变一个阶段，符合广义开尔文模型的蠕变特性。此外，通过室内试验研究发现[5,27]，在不同的应力状态下，岩样由稳态蠕变阶段进入加速蠕变阶段是岩土体材料内部微元应变损伤累积的结果；其宏观表现为轴向应变达到某一数值εc时，岩样进入加速蠕变阶段。相较于单一的完整岩体，软硬互层岩体对元件组合模型的要求更高。

图1 岩体蠕变特性曲线Fig. 1 Creep characteristic curve of rock mass

对此，文中提出了一种考虑应力与应变阈值的黏弹塑性非定常元件组合模型，如图2所示。

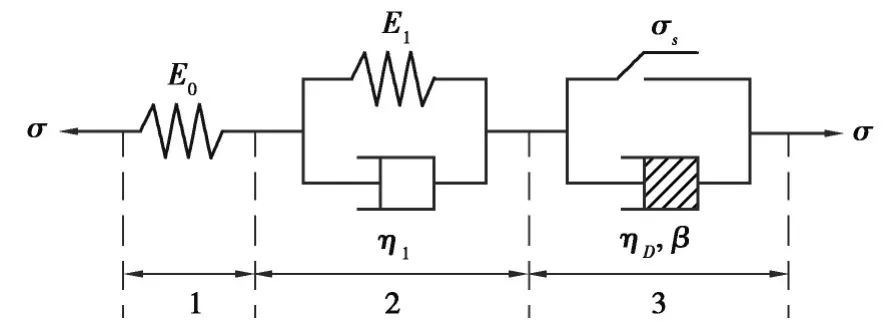
图2 五元件黏弹塑性模型Fig. 2 Five-element viscoelastoplastic model

图2中模型可以充分反映软硬互层岩体蠕变变形的相应阶段，且该组合模型应满足如下3个条件。

1）当σ<σs时，1、2部分所有元件参与蠕变工作，组合模型为三元件模型（H-H/N），可以描述岩体的衰减蠕变阶段的特性，与之相应的状态方程[1]可以表示为

根据式（1）得三元件模型的一维蠕变方程为

2）当σ≥σs且ε<εc时，1、2、3部分所有元件参与蠕变工作，组合模型为五元件模型（H-H/N-S/N），可以描述岩体衰减蠕变阶段和稳态蠕变阶段的蠕变特性，其相应的状态方程可以表示为

根据式（3）得五元件模型的一维蠕变方程为

3)当σ≥σs且ε≥εc时，五元件模型（H-H/N-S/N），可以描述岩体衰减蠕变阶段、稳态蠕变阶段和加速蠕变阶段的蠕变特性，其相应的状态方程可以表示为

式中：σs为岩体蠕变的应力阈值（文中将岩体长期强度作为应力阈值）；εc为岩体进入加速蠕变的应变阈值；tc为与之对应的进入加速蠕变的时间；D为损伤变量[17]，其表达式为

根据式（3）得五元件模型的一维蠕变方程为

1.2 黏弹塑性模型蠕变的三维形式

岩体在实际工程中处于复杂的三维应力状态，其应力张量可分解为球应力张量σm和偏应力张量Sij，其表达式分别为

球应力张量σm能引起物体体积的改变，但不能改变其形状；而偏应力张量Sij只能引起形状改变，但不能改变其体积。相应地，可将岩体的应变张量分解为球应变张量εm和偏应变张量εij，其表达式分别为

一维蠕变方程中岩体的弹性模量E和泊松比ν在三维蠕变方程中应采用与之相应的体积模量G与剪切模量K，可分别表示为

根据式（1）~式（12），结合叠加原理，可得岩体三维应力状态下的蠕变方程

式中：σs为岩体稳态蠕变的长期强度，由室内试验确定；β为非线性牛顿体的元件参数，均由试验确定；H(σ)为单位跃阶函数；F为岩土体材料的屈服函数[28]；Q为塑性势函数，且采用相关联流动法则，其表达式分别为

式中，J2为第二偏应力不变量。

2 黏弹塑性模型数值程序二次开发

2.1 黏弹塑性模型的有限元分析方法

在有限元法的计算过程中，根据前文给出的一维及三维形式的黏弹塑性蠕变方程，需将其表示为相应的增量方程形式。总应变增量Δε包括弹性应变增量Δεe、黏弹性应变增量Δεev和黏塑性应变增量Δεvp三部分为

对图2中1部分弹性元件有：

对图2中2部分黏弹性元件有：

对图2中3部分黏塑性元件有：

则3部分的黏塑性应变增量可表示为

记蠕变增量为Δεc，则有：

式中：D为弹性刚度矩阵；Δσ为应力增量矩阵；Δε应变增量矩阵。

2.2 黏弹塑性模型子程序的二次开发

ABAQUS有限元软件为用户提供了子程序二次开发接口，用户可以使用Fortran语言编写程序，自定义材料子程序（user material subroutine, UMS），通过Standard求解器的接口实现与主程序之间的数据交流。按照ABAQUS非线性增量加载和Newton平衡迭代算法（增量迭代法），软件在每一个增量步对每一个计算单元均调用UMAT，获得Jacobian矩阵DDSDDE（即刚度系数矩阵D），然后通过Standard接口传递给ABAQUS主程序，在主程序完成平衡校核；如果平衡校核不满足误差要求，ABAQUS将继续进行迭代，直至满足误差要求，再进入以下增量步的求解。可见UMAT会被频繁调用，因此要充分考虑子程序代码的质量，提高计算效率。

笔者提出的黏弹塑性模型用于解决与时间相关的非线性问题，其刚度矩阵随时间不断发生变化，每个增量步调用UMAT均需要重新计算刚度矩阵，计算效率大大降低。为此，采用常刚度法进行计算，在时间增量Δtn=tn+1-tn内通过应变增量更新子程序的应力增量和状态变量，根据式（18）~（26）可得：

为提高计算精度，Δεcn采用差分法计算，即：

式中：n是增量步；θ是0~1的积分参数[29]，θ=0对应一个显式Euler积分算法，θ=1对应一个隐式的Euler积分算法。

黏弹塑性本构模型通过UMAT在ABAQUS中实现，每一个增量步开始ABAQUS 主程序在单元的积分点传入应变增量、时间增量步，同时也传入当前已知状态的应力、应变及其他与求解过程相关的变量；UMAT根据本构方程计算应力增量并更新应力及状态变量，提供 Jacobian 矩阵DDSDDE给 ABAQUS 主程序以形成整体刚度矩阵；主程序根据当前荷载增量求解位移增量，完成平衡校核；如果平衡校核不满足误差要求，ABAQUS 将进行迭代直至收敛（笔者判定收敛的标准为平衡校核相对误差小于10-6），然后进行下一增量步。综上，该模型的UMAT主要流程如图3所示。

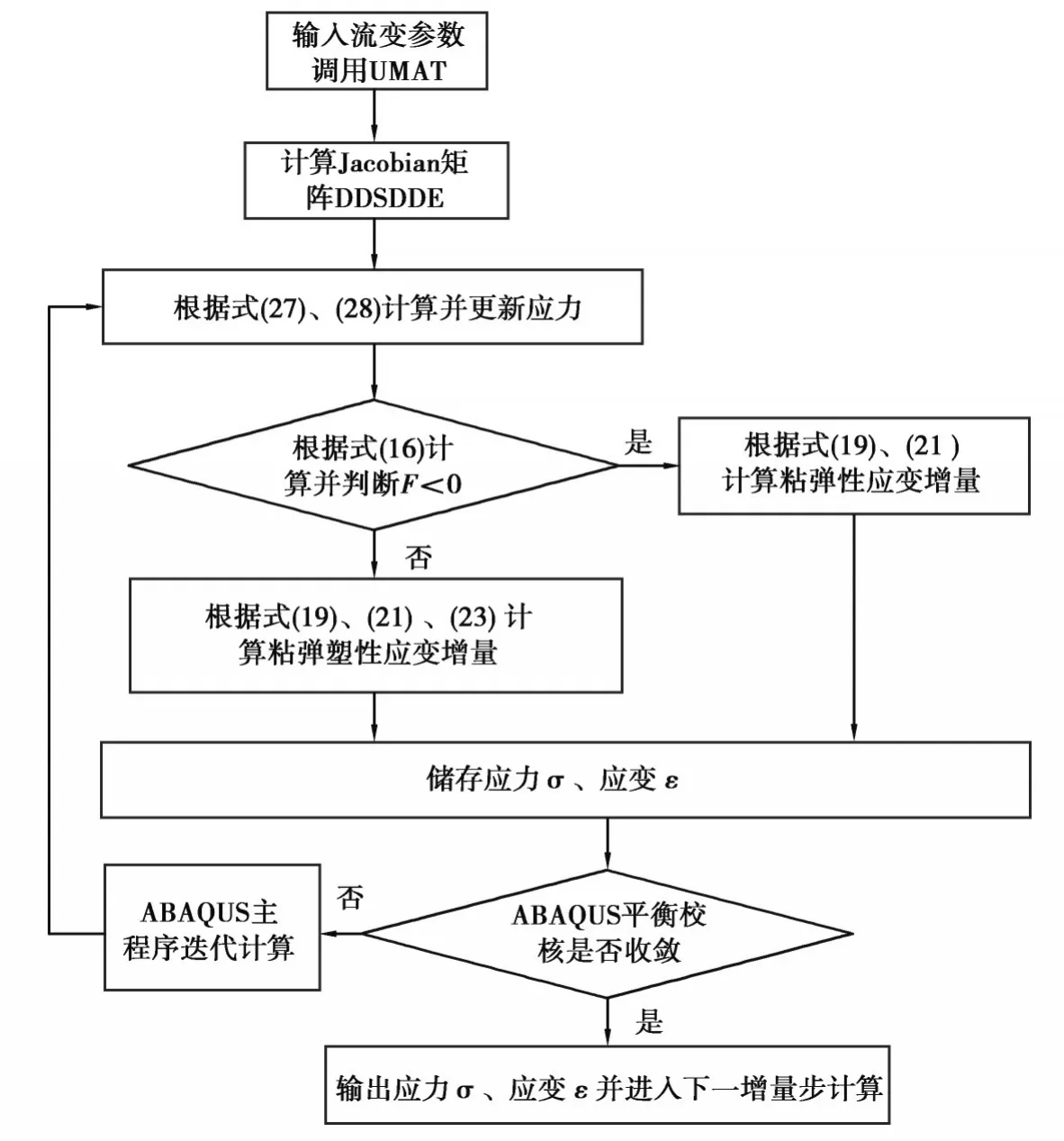
图3 黏弹塑性模型UMAT子程序流程图Fig. 3 Sticky elastoplastic model UMAT subprogram flowchart

2.3 黏弹塑性UMAT算例验证

为了验证文中提出的黏弹塑性五元件模型的正确性与合理性，本算例建立了直径35.5 mm，高70 mm的圆柱体试样模型，且与文献[25-26]三轴流变试验条件保持一致，圆柱体试样底部固定（Ux=Uy=Uz=0），试样顶部施加100 MPa的均布荷载，试样周围施加15 MPa的围压，如图4（a）所示。通过文中开发的黏弹塑性UMAT子程序，在ABAQUS中完成数值计算，轴向应变云图，如图4（b）所示，岩体流变力学参数见表1所示。相比于河海模型（七元件模型），文中模型（五元件模型）组合元件更少，使得2种模型的个别参数存在较大的差异。

表1 蠕变模型参数[10, 26]Table 1 Creep model parameters

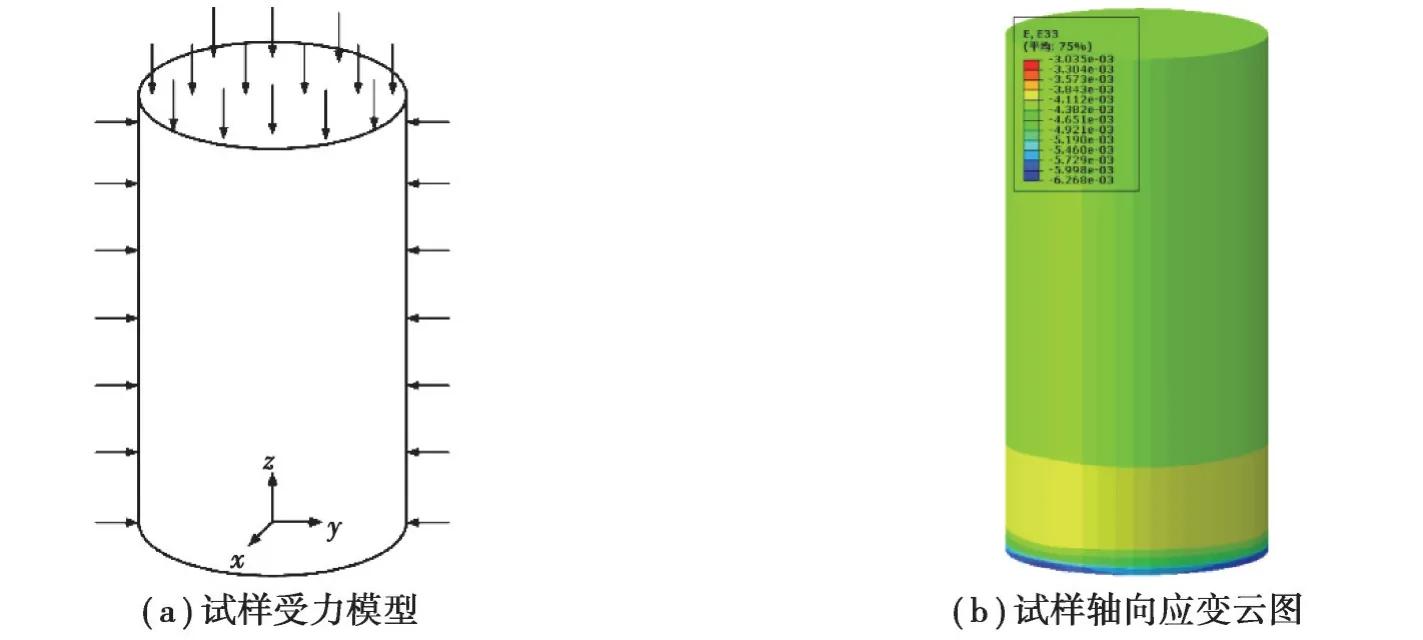
图4 三轴压缩蠕变试验Fig. 4 Triaxial compression creep test

图5给出了圆柱体试样轴向应变蠕变曲线的黏弹塑性五元件模型的UMAT子程序数值计算结果，并与河海模型[10]及其流变试验[26]结果进行了比较。可以发现，文中提出的黏弹塑性模型可以很好地描述岩体蠕变的3个阶段，且基于黏弹塑性模型的UMAT子程序计算结果与河海模型及蠕变试验结果基本一致，从而验证了黏弹塑性模型合理性及UMAT子程序的有效性。

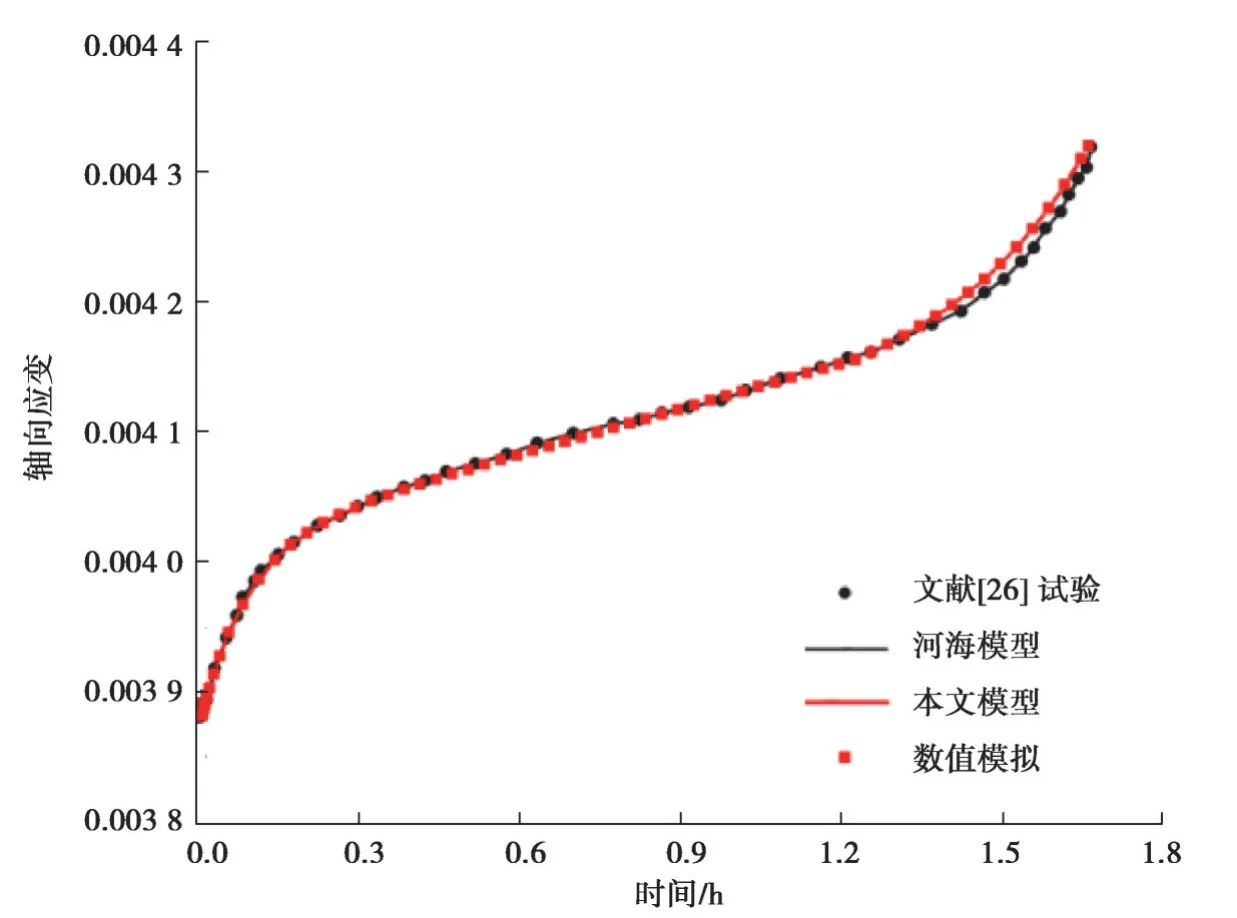
图5 岩体流变模型与试验结果的比较Fig. 5 Comparison of rock mass rheological model and test results

3 结 论

1）根据软岩互层岩体的蠕变特性，将应力、应变阈值引入黏弹塑性蠕变模型，建立了五元件非线性蠕变方程，使其能够同时描述硬岩的线性黏塑性蠕变特性与软岩的非线性黏塑性蠕变特性。

2）通过引入非定常牛顿黏壶改进了Burgers模型，黏壶同时兼顾时间相关性与岩体的微元渐进损伤，使五元件蠕变模型具备了描述减速蠕变、稳态蠕变和加速蠕变的特点。

3）在恒定应力状态下根据一维黏弹塑性本构方程推导出三维黏弹塑性本构方程，并将其用于ABAQUS有限软件UMAT子程序的研发，结合河海模型及其蠕变试验验证了该模型的合理性与有效性。

4）非定常黏弹塑性五元件模型可满足岩体蠕变的各个阶段，通过有限元软件可将其用于隧道工程岩体蠕变的数值分析，为重大岩土体工程的结构设计及长期的运营维护提供理论依据，降低工程实践过程中的潜在风险。