变电站引下线体系时域非线性风振分析

余国庆，晏致涛，王欣欣，刘欣鹏

（1. 重庆大学 土木工程学院，重庆 400044； 2. 重庆科技学院 建筑工程学院，重庆 401331；3. 国网新疆电力公司电力科学研究院，乌鲁木齐 830011）

特高压变电站引下线结构是一种典型的柔性导线结构，其一般为带间隔棒的多分裂软导线，具有跨度小、高差大、线长短、上下连接的特点，对风荷载十分敏感，在风荷载作用下结构变形呈现几何非线性特征。近几年新疆发生多起风荷载作用的引下线损伤事故[1]，2016年阿克苏变电站阿楚一线75321隔离开关的引下线与管母连接金具断裂，现场环境八级大风，导致引下线受力激增，使引下线端部的金具破坏。

对于水平大跨度的分裂导线风振响应已有较多研究，刘小会等[2]对输电线路分裂导线进行模态分析，表明多跨输电导线的低阶固有频率数量级在10−1数量级左右。于永帅等[3]、王述良等[4]得到了气动阻尼和结构频率的关系，表明气动阻尼对水平大跨输电导线的风振响应影响较大，气动阻尼相比结构阻尼占比较高，随着风速的增加，气动阻尼能明显降低结构的风振响应。由于变电站引下线体系布置特性与水平大跨输电线导线差异较大，两者自振频率大小明显不同[5]，对引下线这种小跨度分裂导线模态分析较少，张雪松等[6]研究了软母线及其电气设备的低阶模态。因此，有必要对引下线柔性体系进行风振响应特性分析。

风荷载对于大跨输电导线的风致响应影响已经有较为成熟的规范方法，《架空输电线路荷载规范》[7]采用导地线阵风系数及档距折减系数表征脉动风的影响。风荷载对引下线的影响，《电力工程电气设计手册》[8]中利用空气动力系数kd=1.2进行考虑，对于引下线的风振振动效应并没有合理考虑。有必要对引下线的风振响应放大作用进行研究。在工程中，风振系数一般通过荷载风振系数来定义[9]，但是因为柔性体系的响应与荷载呈现出非线性的关系，定义荷载风振系数在理论上来说是不正确的。根据响应等效原则，江勇[10]提出了响应风振系数。由于非线性的存在，所有响应不能同时等效，又根据响应的不同类型定了义不同类别的响应风振系数[11]。考虑引下线的响应非线性及非高斯性，采用响应风振系数较为合理。

笔者结合阿克苏变电站引下线工程实例，通过AR法[12]模拟脉动风荷载，利用ANSYS软件，通过时域法[13]进行引下线体系的风荷载响应时程分析，并根据响应等效原则，对响应风振系数进行取值，为变电站引下线体系的风荷载计算提供参考。

1 模型参数

利用阿克苏特高压变电站实际线路引下线进行分析，结构布置图如图1所示，图1（a）为结构的真实布置情况，该引下线为四分裂结构，单根引下线型号为JGQNRLH55XK-700，与其连接的管母线型号为6063G-T6-∅200/184，基本参数如表1所示。图1(b)为结构的布置参数，其中，跨度BO=2 m、高差AO=16 m。引下线体系分析利用ANSYS软件建模，模型结构采用BEAM189单元。引下线上端点固结，下端与管母线耦合，管母线两端固结。

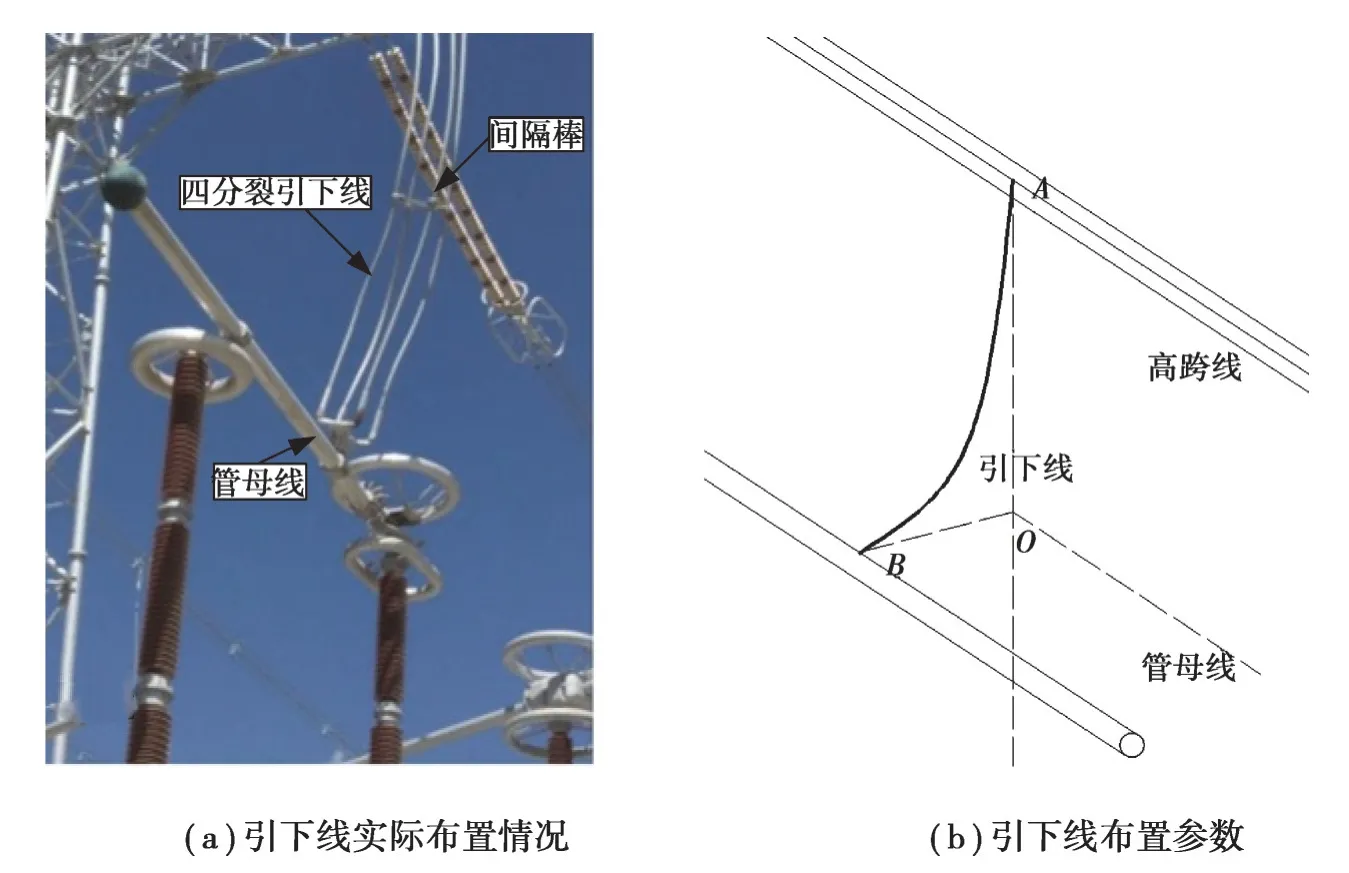
图1 引下线结构图示Fig. 1 Lead-down structure

表1 导线基础参数Table 1 Parameters of the conductor

2 风荷载的模拟

引下线柔性体系受到的主要荷载为风荷载，按照风的基本性质，可以将其分为平均风和脉动风，脉动风对结构的作用是一种随机作用，通常利用随机振动理论来进行分析。对于风荷载的数值模拟，线性滤波法中的自回归（auto-regressive, AR）模型方法因其计算量小、速度快的优点，被广泛用于随机振动和时间系列分析中[14]。文中采用Davenport风速谱[15]，以AR模型通过Matlab编程模拟具有随机性、时间相关性、空间相关性的风速时程。采用Davenport提出的空间相关函数描述空间相关性为

式中：r=x,y,z，一般取Cx=6、Cy=16、Cz=10；基本风压取0.56 kN/m2，场地类别为B类，风速采用指数律风剖面，风速轮廓指数取a=0.15。其他计算参数取值如表2所示。

表2 时程模拟计算参数Table 2 Calculation parameters of time history simulation

根据引下线的位置坐标模拟所有坐标点的风速时程，限于篇幅，仅列出节点1和节点11的部分风速时程曲线（见图2）。由图2可知，AR模型法与目标功率谱吻合较好，同时风速样本的相关函数与目标值也十分吻合，说明该方法能有效模拟随机风速时程。

图2 部分节点风速时程曲线、模拟风谱及相关函数Fig. 2 Wind speed time-history curve, and simulated wind spectrum and correlation function

3 动力特性分析

3.1 模态分析

变电站引下线结构体系一般为四分裂导线，具有跨度小、高差大、线长短、上下连接的特点。在进行引下线体系的动力时程分析之前有必要进行模态分析，获得结构的固有频率及相应振型，具体参数见表3所示。这些指标是进行动力学研究的重要参数。其中：模型1为文中参数的四分裂引下线模型；模型2为同参数的单根引下线模型；模型3为水平布置的四分裂引下线模型；模型4取自文献[16]，为档距353 m的单跨等高四分裂导线模型（表征一般的大跨输电导线）。具体参数及模型如图3所示。

图3 模型1~4布置示意图Fig. 3 Schematic layout of model 1-4

表3 模型结构自振频率Table 3 Natural frequencies of modelsHz

图4为四分裂引下线体系模型1的前4阶模态示意图。第1阶模态为顺着引下线yz面内的整体摆动变形；第2阶模态为xy平面内的上下摆动变形；第3阶模态为耦联体系整体沿y轴方向的扭转变形；第4阶模态为xy平面内的双波弯曲变形，这也与经典的导线模态形式一致[3-4]。

图4 模型1四分裂引下线体系前4阶模态Fig. 4 The first four modes of model 1

值得注意的是，引下线模型（模型1）的振型与模型3的振型变化方式一致，自振频率也比较接近，除第2阶自振频率外，平均差值为2.3%，而模型3与模型4相比，自振频率相差了一个数量级。文献[5]对悬索导线的自振频率进行了研究，自振频率主要由跨度l和水平张力T控制，在跨度较小时，导线的自振频率会明显变大，文中计算结果与其基本相符。而四分裂导线模型1比单导线模型2前5阶平均高1.6倍，由单根导线扩展为四分裂导线时，T也会明显变化，文献[17]中对此也进行了验证。几个模型的对比说明引下线体系与一般大跨度导线不同，因其线长及跨度较短、高差较大的特点，其自振频率较大，因此二者动力响应特性也有着明显的差别。

3.2 动力时程响应

根据第2节中模拟的不同风速下的脉动风速时程曲线，利用ANSYS有限元软件对模型1进行风荷载动力时程分析，利用非线性参数设置，通过Newton-Raphson迭代法可以考虑由于结构几何非线性变形引起的结构响应问题。模型部分节点的反力响应曲线和位移响应曲线如图5所示。对于一个确定性的、非时变的线性系统，如果随机激励是平稳的、高斯分布的，则结构响应也将是平稳高斯分布的。但是对于一个非线性程度较高的结构系统，响应可能呈现出非高斯分布，如一些大跨度膜结构[13]。结构的几何非线性行为是引起响应非高斯的一个重要因素，引下线模型在风荷载作用下，产生几何大变形，其响应的频率分布见图5[18]所示，频率分布不符合高斯分布，不能直接利用准定常理论下表征动力响应。在工程上，为了体现脉动的影响和方便工程设计，采用荷载风振系数来考虑风荷载的动力效应。根据风振系数（静动风荷载与静力风荷载的比值）定义，在实际应用时，按照静力等效风荷载的原理来计算风振系数，其目的是保证结构在动荷载作用下的结构最大响应一致。但是，分析表明，由于引下线体系与风荷载呈现非线性关系以及结构响应的非高斯性，这种模式下荷载风振系数理论存在缺陷。

图5 节点响应时程曲线及其频率分布图Fig. 5 Response time history curve and frequency distribution of lead-down node

4 参数分析

基于四分裂引下线体系的动力特性，其布置的跨高比L/H、间隔棒的数量N，均会改变引下线的刚度，从而影响结构的动力响应；同时，风速V的大小、风向角θ和气动阻尼ξa也会影响结构的动力响应。故设置气动阻尼、风向角θ、风速V、跨高比L/H和间隔棒数量N等多种不同参数的工况，研究不同参数对引下线结构的风振响应的影响。

4.1 气动阻尼比的影响

对于跨度较大的输电线路导线，导线的气动阻尼相对于结构阻尼，占主导地位，不考虑气动阻尼将会高估输电导线的风振响应[3-4]。气动阻尼主要受到风速V和结构自振频率ƒ及振型的影响，文献[4]提出气动阻尼计算式为

式中：CD为阻力系数，CD=1.2；ρa为空气密度，ρa=1.293 g/L；d为单导线直径；m为单导线单位重量；V为导线上平均风速大小；fi为模型的第i阶自振频率为作用在输电导线单位长度上的平均风荷载。

由表3可知，引下线结构其前四阶自振频率较大跨导线结构大，因此在控制其他参数相同时，引下线的气动阻尼要比大跨导线结构的气动阻尼小。文献[4]通过试验测试，识别导线振型阻尼比取值0.97%，文献[16]中对索网结构的结构阻尼比建议取1%，将引下线自身阻尼比ξs取值1%。在计算引下线的气动阻尼比时，阻尼矩阵中包含了气动阻尼的影响项：ξ=ξs+ξa，通过求解阻尼矩阵，用总阻尼比减去结构阻尼比，即可得到结构不同风速下的气动阻尼比ξa。通过上述方法，计算了不同风速下的模型1和模型4的气动阻尼比，并与式（2）、（3）进行比较，具体结果见图6所示。其中：Fz、Fx表示是风荷载的作用方向，A表示由ANSYS拟合而得，E表示由公式计算而得。由图6（a）可知：ANSYS拟合的模型4的气动阻尼比和式（2）、（3）较为吻合，且模型1的气动阻尼比明显低于模型4的气动阻尼比，即相较于大跨度导线，引下线结构的气动阻尼较小；不同风向作用下的气动阻尼也不一样，平面外的气动阻尼比要高于平面内的气动阻尼比，平面外的气动阻尼比较平面内的气动阻尼比平均高40%。图6（b）展示了平面内气动阻尼比对模型1的响应的影响，模型1的反力最大值，考虑了气动阻尼之后，随着风速的增加，气动阻尼的效应越强，在30 m/s风速时差距为5.3%；对于位移响应的最大值，二者最大差距不超过6%。以上结果表明引下线体系结构与传统水平大跨度输电线路风振响应不同，气动阻尼对引下线体系的风振响应影响较小。

图6 气动阻尼分布及对应引下线体系动力响应Fig. 6 Distribution of aerodynamic damping and dynamic response of lead-down system

4.2 风向角的影响

在3.1节中，分析了引下线体系的前4阶模态，前2阶模态分别是yz平面和xy面内的摆动。由于结构的响应主要是低阶模态起控制作用，不同的风向角会影响结构的响应，设计风速下不同风向角的响应极值分布如表4所示，反力在0°风向角(x轴)最大，位移在90°风向角(z轴)最大，并在这2种最不利工况下研究不同风速下的响应分布，结果如图7所示。

图7 风向角对引下线体系的风振响应的影响Fig. 7 The influence of wind direction angle on wind-induced response of lead-down system

表4 不同风向角下的响应极值分布Table 4 Distribution of response extremum at different wind directions

由图7可知，随着风速的增加，结构响应越大，0°风向角时下的反力响应比90°风向角下的反力响应的均值和最大值平均的大32.6%和25.6%；位移响应的均值和最大值平均的小44.5%和43.3%。由于引下线平面内外刚度的差异，导致弱轴方向容易变形，但是在强轴方向反力响应会增强。为保证引下线结构的安全，建议设计时需考虑0°风向角和90°风向角的荷载效验结构强度及变形要求。

4.3 跨高比的影响

跨高比L/H直接影响了引下线的外形，外形的改变会直接导致结构的力学性能的变化，设置了3种不同跨高比的工况进行比较：在模型1的基础上，保持其他参数一致，将跨度L分布从2 m增加至3 m和4 m，分别用L2、L3、L4表示3种不同跨度的工况。通过计算，得到了各节点的风振响应结构反力和位移的均值及最大值的结果。从图8可以看出：风速V直接影响引下线体系反力响应的均值和最大值，随着风速的增大，引下线体系的反力响应和位移响应均增大，结构动力响应变得剧烈。跨高比L/H的增加会增加引下线体系的刚度，导致结构反力响应增加，而位移响应减小。实际布置引下线时，跨高比不宜过大。

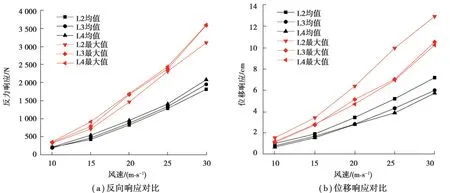
图8 跨高比对风振响应的影响Fig. 8 Effects of span-height ratio on wind-induced response

4.4 间隔棒数量的影响

间隔棒一般为铝合金材料，用于约束分裂导线间的相对运动，同时也是为了满足设备的电气性能，防止导线之间的鞭击。文中选用的四分裂间隔棒单重为11.8 kg，计算了30 m/s风速下，隔棒数量为N=7，N=6，N=5，N=4，N=3，N=2六种工况下的引下线节点的响应分布，结果如图9所示。

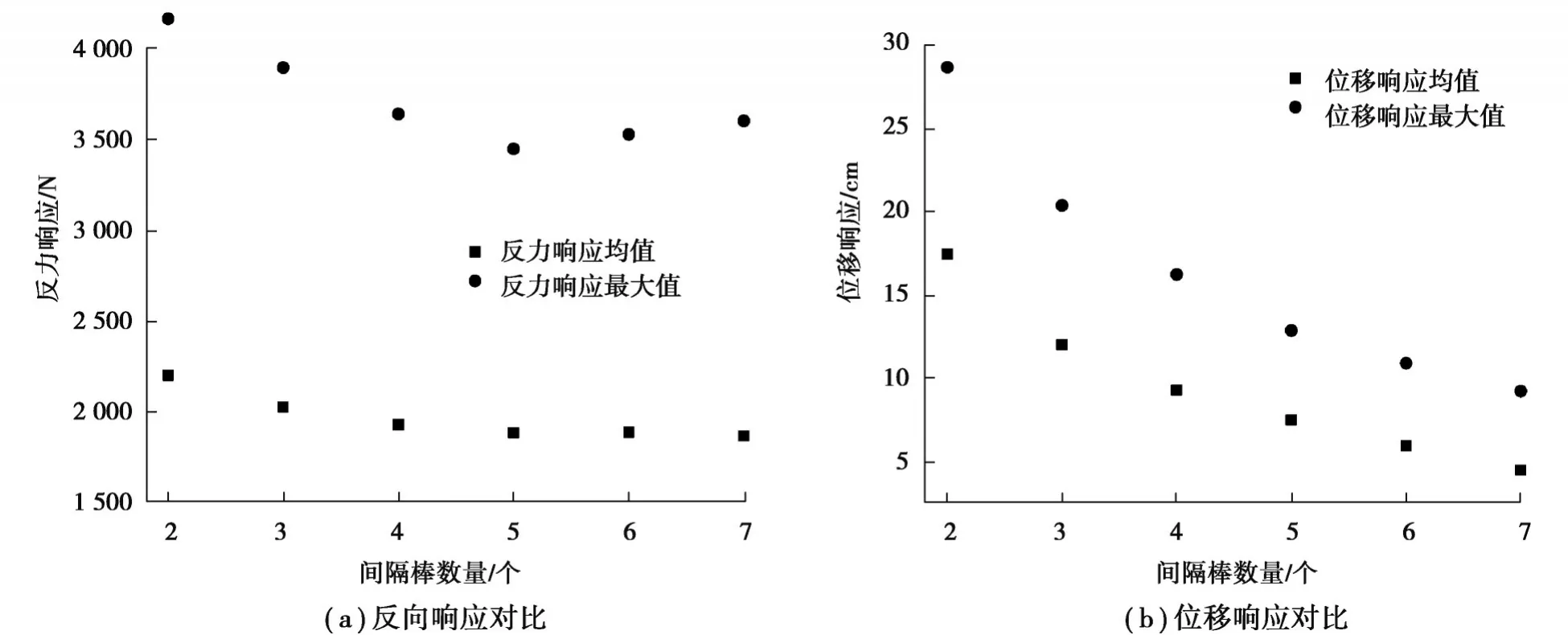
图9 不同间隔棒数量对风振响应的影响Fig. 9 The influence of the number of spacer on the wind-induced response

由图9可知：间隔棒的数量N会影响引下线体系的整体刚度，从而导致动力响应的不同，位移响应的分布由于间隔棒数量的增加而减小；而结构的反力响应则随着间隔棒数量的增加而减少，但随着间隔棒重量在引下线结构的比例增加，反力响应而后增加。结果表明，间隔棒数量N，会影响引下线体系的整体刚度，合理考虑间隔棒数量能改善体系的受力性能。

5 响应风振系数

由3.2节可知，引下线结构的响应具有非高斯性，荷载风振系数的定义不适用于本模型，因此参考文献[9]的建议，对于引下线体系应该确定其响应风振系数。按照响应的类别不同，又可以分为位移响应风振系数和内力响应风振系数。

式中：βi(z)表示响应风振系数，其中下标i=s,f分别表示位移和内力；P(z)风荷载作用下的最大响应；Pc(z)静风作用下的平均响应。在30 m/s的设计风速下，不同参数下的响应风振系数如表5所示。

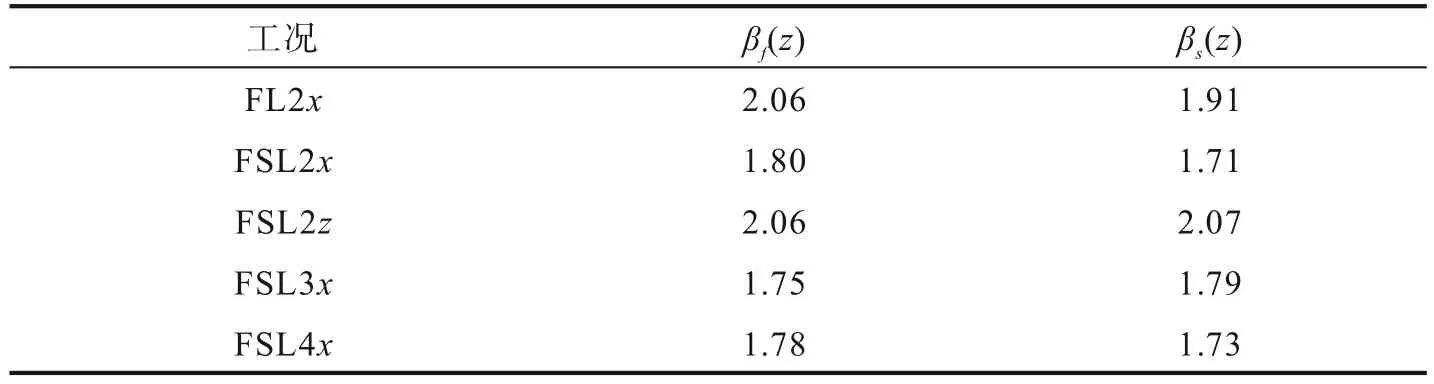
表5 不同工况下的风振系数Table 5 Wind vibration coefficient under different working conditions

表5中，F表示没有考虑气动阻尼；FS表示考虑气动阻尼、L(2/3/4)表示跨度；x和z分别表示风荷载方向。由表5可知，由于引下线体系的强非线性，不同参数作用下引下线反力响应风振系数和位移响应风振系数并不一致，考虑气动阻尼时，响应风振系数降低。随跨度增大，风振系数呈减小趋势，且平面外风振系数明显大于平面内。

6 结 论

通过对脉动风荷载的模拟和引下线体系动力特性的分析，以及风荷载动力时程响应分析得到以下结论：

1）由于引下线体系有着较高的几何非线性，其风振响应存在着明显的非高斯性，结构响应和荷载并不成线性关系，直接使用响应方差来表达动力性能不再适用，建议采用响应风振系数表征风振响应动力荷载。

2）由于引下线结构较以往大跨输电导线而言线长较短，结构自振频率较大，与水平大跨度输电线路风振响应不同，引下线结构的气动阻尼较小，风振响应受气动阻尼影响较小。

3）0°风向角下的引下线反力响应最大，而90°风向角下的引下线位移响应最大；同时跨高比L/H的增加会导致结构的反力响应增大，而位移响应减小；间隔棒数量也直接影响引下线体系的整体刚度，结构的位移响应随着间隔棒数量的增加而减少，反力响应随间隔棒数量先减少而后增加。

4）设计风速下的风振系数分析表明，不同参数作用下引下线反力响应风振系数和位移响应风振系数并不一致。考虑气动阻尼，风振系数降低。随跨度增大，风振系数呈减小趋势。平面外响应风振系数明显大于平面内。