剪力墙构件恢复力模型在OpenSees中的应用

罗国胜，顾冬生

（江南大学 环境与土木工程学院，江苏 无锡 214122）

钢筋混凝土剪力墙因具有较大的抗侧刚度，能有效控制结构水平位移，而广泛应用于高层与超高层建筑结构中。虽然高层结构总体抗震性能良好，但是在历次大地震中高层结构出现严重损坏的案例也屡见不鲜，在2010年智利地震[1]和2011年新西兰地震[2]中大量剪力墙出现严重破坏，表明对于剪力墙抗震性能还需进一步研究，特别是对于剪力墙变形能力相关的计算。大量的研究表明：数值计算已经成为高层结构抗震研究的一个有效手段，其中OpenSees (open system for earthquake engineering simulation)作为一款有限元软件已经得到广大研究人员的重视，其丰富的材料库和单元库，以及高效的算法使之成为抗震领域重要的开放科研平台[3]。

对剪力墙受力行为的模拟可以有很多方法，在OpenSees中可以采用纤维梁柱单元来模拟，该模型能较好地考虑弯矩和轴力的耦合，但是不能直接考虑剪切变形，一般要结合另外的单元来模拟剪切变形[4]。近年来能考虑弯曲和剪切耦合作用的SFI模型（shear-flexure interaction model，SFI）得到了较多的应用[4]。国内陆新征等[5]开发了精细分层壳单元来模拟剪力墙弯剪行为，也得到了满意的效果。总体上这几种方法，模拟精度都比较高，但模型单元多、计算量大、计算效率较低。

对于剪力墙变形能力的计算方法已经有了较多的研究。Abdullah等[6]通过对164片剪力墙进行参数分析，提出了剪力墙位移能力的计算公式，并与剪力墙试验结果比较，验证了计算公式的准确性。梁兴文等[7-8]通过截面分析计算了矩形剪力墙的屈服位移，提出剪力墙的4折线弯矩-曲率模型并计算了关键点，但提出的模型没有考虑剪切变形，且对比的试验数据较少，精确度有待研究。张松等[9]通过15片剪力墙拟静力试验提出了剪力墙三折线骨架曲线并给出了关键点计算方法，但拟合公式的参考数据较少，试件参数的范围也有一定的局限性。钱稼茹等[10]通过较多的剪力墙试验数据回归出了屈服转角和极限转角的计算公式。李宏男等[11]提出了RC剪力墙的多弹簧宏观计算模型，并通过9片剪力墙试验验证了模型的正确性。

在上述相关研究的基础上，笔者提出剪力墙构件的恢复力模型，骨架曲线用弯矩-转角三折线模型来定义。收集了105片剪力墙试验数据，提出了考虑剪跨比影响的有效刚度计算公式，研究了受弯承载力最大值计算方法，对现有的剪力墙变形能力计算模型进行评估，对于承载力和刚度退化行为，采用OpenSees中成熟ModIMK滞回规则进行模拟。提出的恢复力模型可以直接用于模拟剪力墙从弹性到弹塑性，以及最后进入软化段全过程的非线性变形行为。与精细的SFI模型和分层壳模型进行比较表明，文中提出的模型有足够的精度，计算效率高收敛性好，并通过增量动力分析(incremental dynamic analysis, IDA)来进一步验证该模型的有效性。

1 恢复力模型骨架曲线

1.1 三折线骨架曲线

剪力墙在侧向荷载作用随着侧向荷载的增加，墙体经历混凝土开裂和钢筋屈服等过程，侧向荷载达到最大值后逐步下降，墙体发生破坏。这一过程可以简化为三折线模型，如图1所示，分为屈服段、强化段和软化段。受拉区最外侧混凝土开裂前，剪力墙处于弹性阶段，当侧向位移角达到θ′y时，剪力墙首次屈服，M′y为首次屈服弯矩，定义为最外侧混凝土压应变达到0.002或者最外侧受拉钢筋屈服时弯矩的较小值[12]。当轴压较小时一般钢筋受拉屈服先于混凝土受压屈服。My为屈服弯矩，取最外侧混凝土压应变达到0.004时的截面弯矩[12-13]。构件达到屈服弯矩后，一般受弯承载力会有一定上升，其最大值Mc为峰值弯矩，峰值位移角为θc。

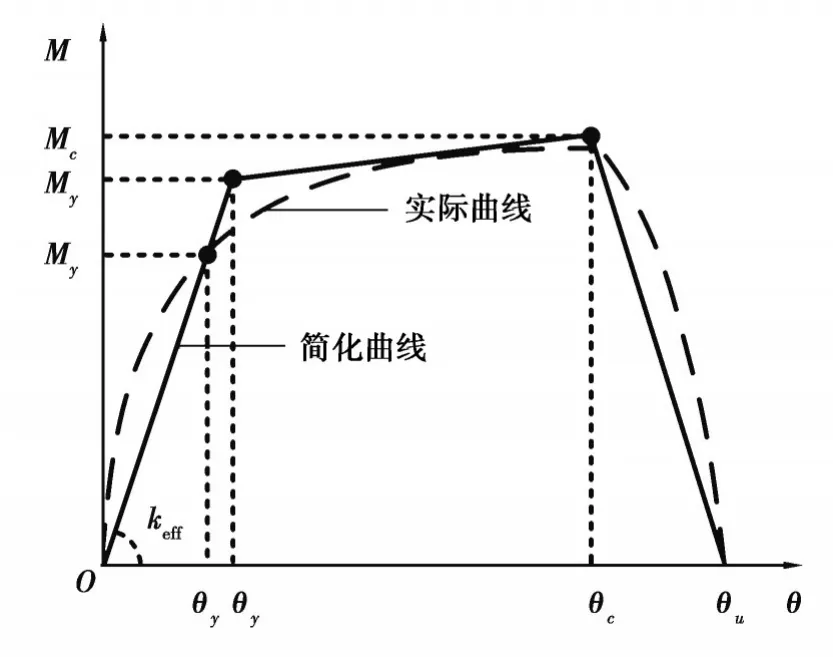
图1 剪力墙弯矩-转角骨架曲线Fig. 1 Moment-Angle skeleton curve of shear wall

1.2 弹性段定义

侧向位移位移角可以表示为屈服位移角θy和塑性位移角θp之和

对于悬臂剪力墙弯曲变形，根据弹性理论

式中：EcIeff为截面有效刚度；heff为剪力墙高度。钢筋混凝土剪力墙侧向位移主要由弯曲、剪切、底部钢筋从基础中滑移引起的侧向变形3部分组成，滑移变形一般相对较小，不足10%。当剪力墙剪跨比较小时，剪切变形不能忽略，试验表明剪跨比低于1.0时剪力墙的剪切变形能达到总变形的50%左右，所以要通过试验结果研究剪跨比对截面有效刚度的影响。

2 截面有效刚度计算

2.1 现有的计算模型

当剪力墙剪跨比变小时，剪切变形占比会逐渐增加，可以通过减小式(3)截面有效刚度来考虑剪切变形的影响。Paulay等[14]通过试验研究与数值分析提出了考虑剪切变形的剪力墙截面有效刚度计算公式

式中：EcIg为剪力墙毛截面刚度；fy为纵筋屈服强度；lw和bw分别为剪力墙截面的长和宽；n为轴压比；F为

由式(4)和式(5)可以看出随剪跨比heff/lw增大，F减小，从而截面有效刚度增大。当fy取400 MPa，n=0.1时，heff/lw从1.5增加到3，EcIeff/EcIg从0.22增加到0.27。

Li等[15]在Paulay等[14]研究基础上对剪跨比小于2.0的试件进一步研究，提出了截面有效刚度的建议公式，为

同样的heff/lw从1.5增加到3，EcIeff/EcIg从0.12增加到0.29。可以看出在剪跨比较小时，式(6)计算结果显著小于式(4)。

Haselton等[16]对钢筋混凝土柱试验结果研究认为截面有效刚度只与轴压比n和剪跨比heff/lw有关，并在大量试验数据基础上提出

2.2 截面有效刚度试验结果

为了验证截面有效刚度计算方法，笔者对国内外试验结果进行总结。选择矩形截面两端有约束边缘的试件，端部约束区箍筋间距不超过100 mm，箍筋间距与纵筋直径比值不超过10，以保证塑性变形区有较好的约束。共收集了105片剪力墙试验结果，剪跨比范围为1.0~6.0，轴压比范围为0~0.51，基本涵盖了剪力墙工程参数常用范围。对于每个试件，用OpenSees建立剪力墙的纤维模型，通过截面分析，提取墙截面最外侧混凝土压应变达到0.004时的截面弯矩作为屈服弯矩理论值My；根据试验屈服位移，通过式(3)计算截面有效刚度试验值。剪力墙基本信息和计算结果见表1所示。根据公式(4)、(6)和(7)计算截面有效刚度，图2给出了有效刚度计算值和试验值的比与剪跨比的关系。

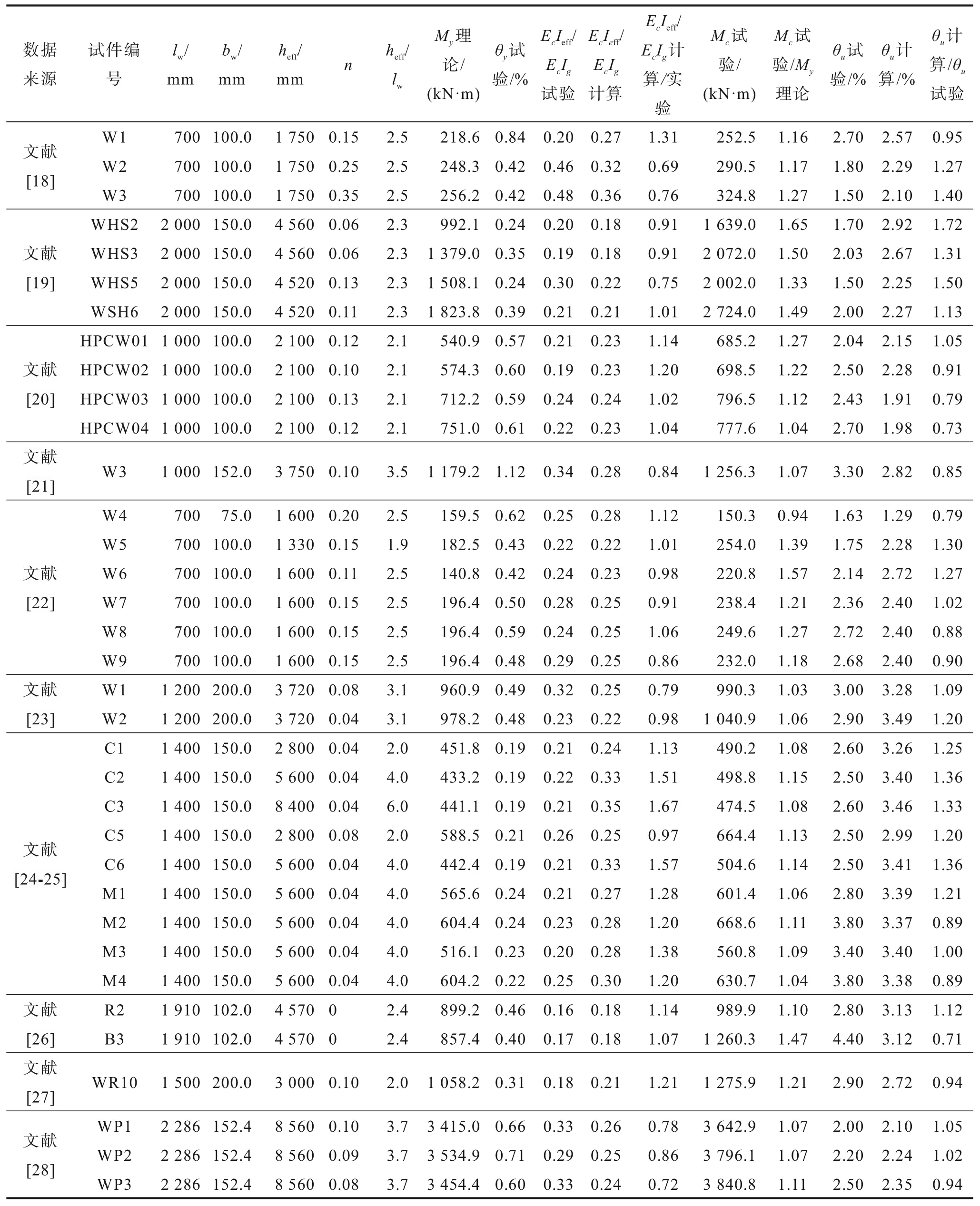
表1 试验数据与计算结果Table 1 Test data and calculation results

图2 有效刚度计算结果与剪跨比的关系Fig. 2 Relationship between effective stiffness calculation results and shear span ratio

式(6)是通过低剪跨比的试验结果回归出来的，适用于低剪跨比的截面有效刚度计算，其计算值与实验值比的平均值为1.03，离散系数为0.62。heff/lw在2.0~6.0范围内式(4)和式(7)的计算结果与试验值吻合较好，但在heff/lw小于2.0时误差相对较大，计算结果都偏大的比较多。从图2结果可以看出总体上式(4)的计算结果精度最好，笔者对式(4)进行了系数调整：

图3给出了文中建议的式(8)计算结果与剪跨比的关系，在剪跨比小时计算精度有所提升，截面有效刚度计算值与试验值比值的均值1.04，离散系数0.26，说明调整后的计算公式可以较为准确地预测截面有效刚度。

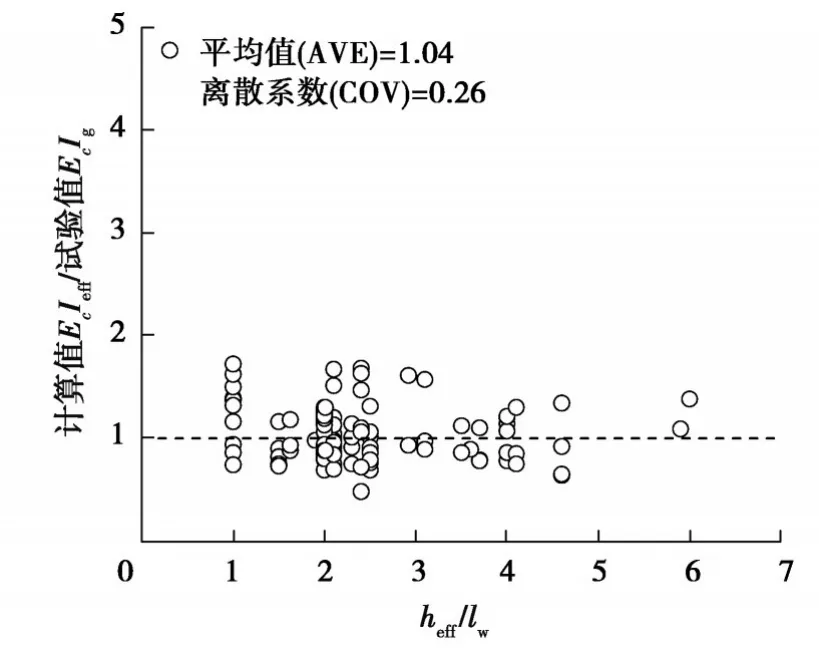
图3 式(8)计算结果与剪跨比的关系Fig. 3 Relationship between the calculation results of equation 8 and shear span ratio

对于截面屈服弯矩My，文中用的是OpenSees计算的值，也可以根据Panagiotakos等[17]提出的公式进行计算。文中也对这2种计算结果进行了比较，根据统计，公式计算值与程序计算值比值的平均值为1.0，离散系数为0.13，说明文献[17]提出的方法计算结果精度很高，可以用于计算屈服弯矩。

3 强化段定义

3.1 峰值弯矩确定

剪力墙进入塑性阶段后，随着位移增加，受弯承载力会有所增大，这是由于钢筋进入强化阶段以及混凝土受到箍筋约束共同作用的结果，承载力达到峰值之后开始进入下降段，直到剪力墙破坏。根据文献[42]对于RC柱受弯承载力的研究，峰值弯矩Mc为

计算了收集的105片剪力墙的峰值弯矩，并与实验值对比，计算值与实验值比值的平均值为1.11，离散系数为0.17，计算结果相对偏大。图4给出了105个试件Mc试验值与My理论值的比值与轴压比的关系，可以看出轴压增加对弯矩的增长效果并不显著，主要是剪力墙的轴压比一般较小，绝大部分在0~0.3之间，所以影响较小。从图4可以看出，Mc/My均值为1.10，离散系数为0.17，离散较小。峰值弯矩Mc可由式(10)进行简化计算，对于RC柱，文献[42]建议这一比值为1.13。

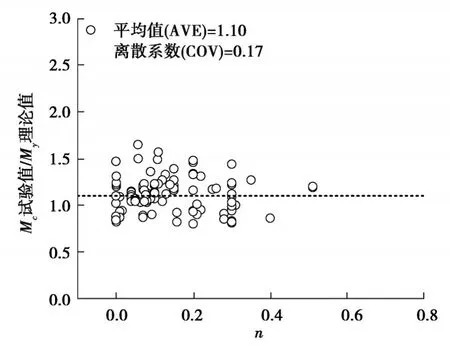
图4 弯矩增强系数与轴压的关系Fig. 4 Relationship between moment enhancement factor and axial pressure ratio

3.2 峰值转角的计算

剪力墙变形达到一定值时，底部塑性区的破坏逐渐严重，受压区约束混凝土出现压碎，局部钢筋出现屈曲，承载力迅速下降，构件发生破坏。对于峰值变形能力主要与轴压比和约束区箍筋用量有关[9]。近年来Abdullah等[6]经过大量大尺寸试验研究发现，当约束箍筋满足一定要求时，峰值变形能力主要与受压区高度和截面的长宽比（lw/bw）相关，箍筋的用量不会影响变形能力，随着截面宽度增加，峰值变形能力能有较大增加。这也和大量剪力墙震害现象吻合，截面宽度小时，剪力墙破坏特别严重[2]。文献[6]在试验研究基础上提出了峰值位移的计算公式

式中：vmax为最大剪应力，通过峰值弯矩计算值计算；c为最外侧混凝土应变0.004时受压区高度。受压区高度一般与轴压比和纵筋配筋率有关。文献[43]提供了的63片矩形剪力墙混凝土应变达到0.004时的受压区高度，根据这些数据进行回归分析，提出

式中：kf为腹板纵筋配筋特征值，kf=ρwfyw/fc计算，式中ρw为腹板纵筋配筋率，fyw为腹板纵筋屈服强度。

计算结果与文献[43]的数据对比见图5所示，计算值与对比数据的比值平均值为1.04，离散系数为0.24，可以看出计算结果较好，说明式(11)可以比较准确地计算剪力墙受压区高度。

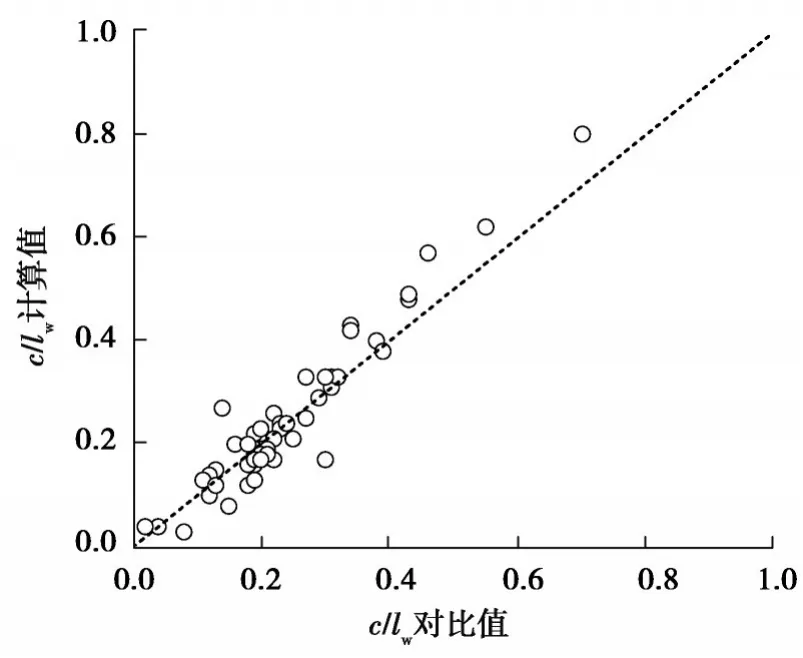
图5 式(11)计算结果Fig. 5 Calculation results of equation 11

用式(11)计算文中收集的105片剪力墙峰值转角，受压区高度由式(12)计算，计算值和试验值的比值与约束区箍筋的配箍特征值关系见图6所示，比值平均值为1.03，离散系数为0.29，计算结果离散性较小。

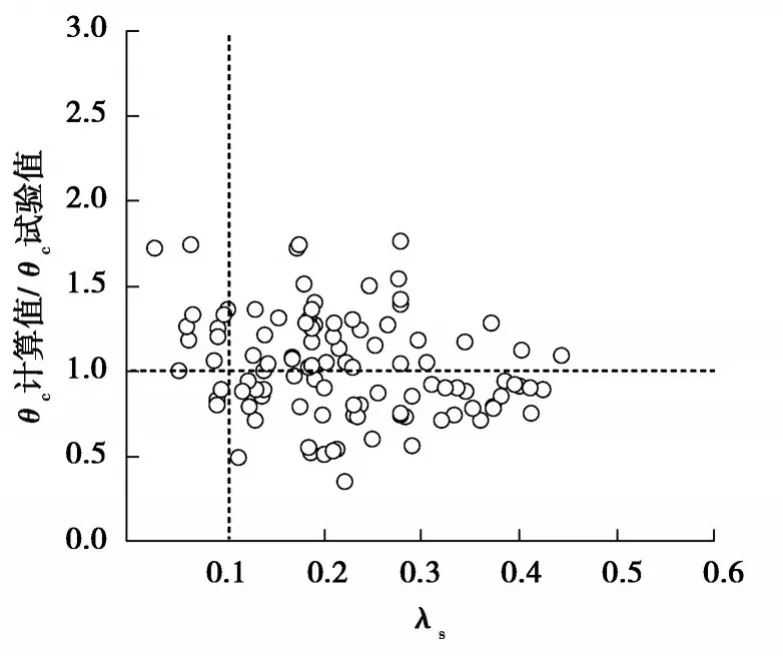
图6 峰值转角计算精度与配箍特征值关系Fig. 6 Relationship between the peak rotation

从图6 可以看出对于配箍特征值小于0.1的13个试件，计算值大于和等于试验值的试件数量有11个，说明在箍筋用量较小时，式(11)的计算结果偏大。当配箍特征值大于0.1时，计算值与试验值比值大于1的试件数量并不明显多于小于1的试件数量，说明不考虑箍筋用量不会显著影响计算精度。图6统计结果表明在箍筋用量较少时，增加箍筋用量对变形能力是有利的，这和文献[10-11]结论吻合，当箍筋用量达到一定量时再增加，就不能显著增加剪力墙的变形能力；另外，文献[44]通过对端部有约束箍筋的剪力墙试验进行分析也得到了类似结论，并建立有限元模型进行了验证。这一现象的主要原因是随着箍筋用量的增加，剪力墙的破坏从混凝土受压破坏转变为纵筋屈曲受拉断裂破坏为主，而当箍筋间距满足一定要求时，箍筋用量的进一步增加并不能显著增加纵筋的抗屈曲断裂的能力。根据这些讨论，说明式(11)适用于箍筋用量较多的试件，在应用时要予以注意。

4 数值模拟

4.1 低周反复模拟

4.1.1 滞回规则确定

选择OpenSees中的可以考虑强度与刚度退化的ModIMK材料来定义剪力墙的滞回规则，如图7所示，剪力墙的骨架曲线关键点用文中提出的计算方法计算。剪力墙在往复加载下耗能增加，会出现强度和刚度退化[45]，在ModIMK材料中可以通过4个退化系数来控制，分别是屈服强度退化系数、峰值后强度退化系数、卸载刚度退化系数和再加载刚度退化系数。

退化由能量耗散能力Et控制，根据Haselton等[42]，能量耗散能力Et由屈服弯矩My和峰值转角θc计算，计算公式为：

式中，λ为能量耗散系数，Haselton等[42]建议λ=30(0.3)n。ModIMK材料中4个退化系数可取相同值[42]，其表达式为30(0.3)nθc。由于剪力墙变形能力相对于RC柱明显偏小，其强度和刚度的退化并不明显。

根据文献[45]，骨架曲线过了峰值点进入下降段的刚度kc=αckeff。对于RC柱，αc根据约束箍筋情况取-0.1~-0.5；对于剪力墙，承载力进入下降段一般破坏比较迅速，这里建议取-1，由此可以计算最终破坏时的转角大小。

4.1.2 滞回模型应用

应用文中提出的滞回模型，采用OpenSees对剪力墙试验进行了模拟，这里给出了文献[29]中的C10剪力墙模拟结果。剪力墙试件部分参数见表1，保护层厚度为27 mm，混凝土强度32.7 MPa；边缘约束区配有20根直径为16 mm的纵筋，屈服强度为543 MPa；约束箍筋直径为6 mm，箍筋间距65 mm；腹板区长1 430 mm，共配20根直径10 mm纵筋，屈服强度为507 MPa。图8给出了剪力墙对称截面配筋信息。

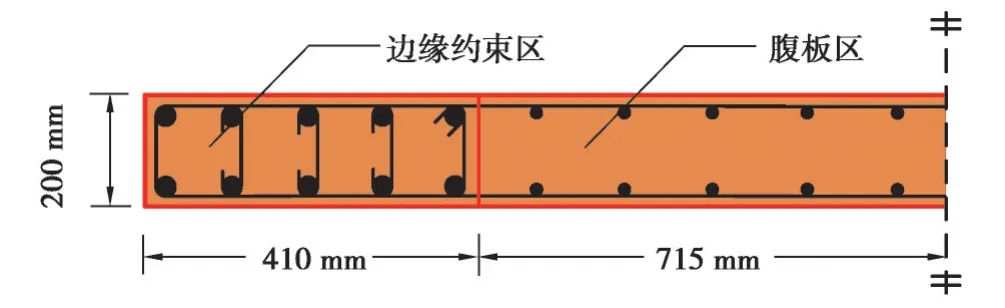
图8 C10剪力墙截面Fig. 8 Shear wall section of C10

剪力墙的ModIMK分析模型如图9所示，OpenSees建模时，剪力墙采用弹性单元(elasticBeamColumn element)模拟，底部设零长度单元(zeroLength element)，通过ModIMK材料来定义零长度单元转动关系来模拟剪力墙变形，其材料本构关键点采用文中提出的计算方法计算。表2列出了C10关键点计算结果，可以看出计算结果精度较高，说明文中提出的三折线计算模型能有效预测剪力墙的受力行为。

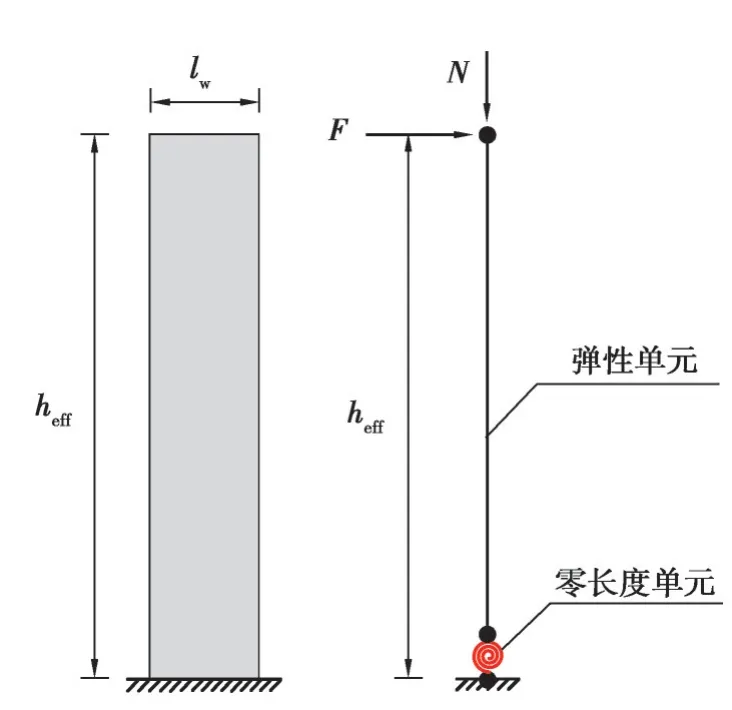
图9 C10剪力墙ModIMK模型Fig. 9 Shear wall ModIMK model of C10

图10为剪力墙数值模拟结果和试验结果对比，从图中可以看出两者曲线吻合较好，强度、刚度退化也能很好模拟。计算的峰值位移点和试验结果比较接近，在加载负方向，计算结果很好地模拟了破坏过程。

图10 C10 ModIMK模型模拟结果Fig. 10 ModIMK model simulation result of C10

4.1.3 与分层壳模型对比

文献[5]开发的基于OpenSees平台的分层壳单元可以很好地模拟剪力墙受力过程，在应用时，腹板区和边缘约束区分别由不同层数的钢筋和混凝土材料层组成，通过定义每一层钢筋或混凝土本构来计算单元的应力和应变。谢琳琳等[46]用这一单元对文献[41]中试件SW1-1进行了模拟，剪力墙高2 000 mm，墙截面长为1 000 mm，宽125mm；混凝土强度为20 MPa，剪力墙轴压比为0.1；单测边缘约束区长200 mm，配有6根直径为10 mm的纵筋，屈服强度为352 MPa，约束箍筋直径为6 mm，箍筋间距为80 mm，屈服强度为392 MPa；腹板区配10根直径为6 mm的纵筋。

建立剪力墙的ModIMK模型，建模方法与上文一致。低周反复模拟结果如图11(a)所示，按2个方向骨架曲线平均值计算，屈服位移试验值为6.4 mm，模拟结果为5.3 mm，比试验值小17%，峰值剪力分别为195 kN和183 kN，误差只有6%，可以看出ModIMK模型屈服点、峰值点和破坏段都与试验结果吻合很好，特别是负方向过了峰值点的下降段很准确地模拟了试验破坏过程。

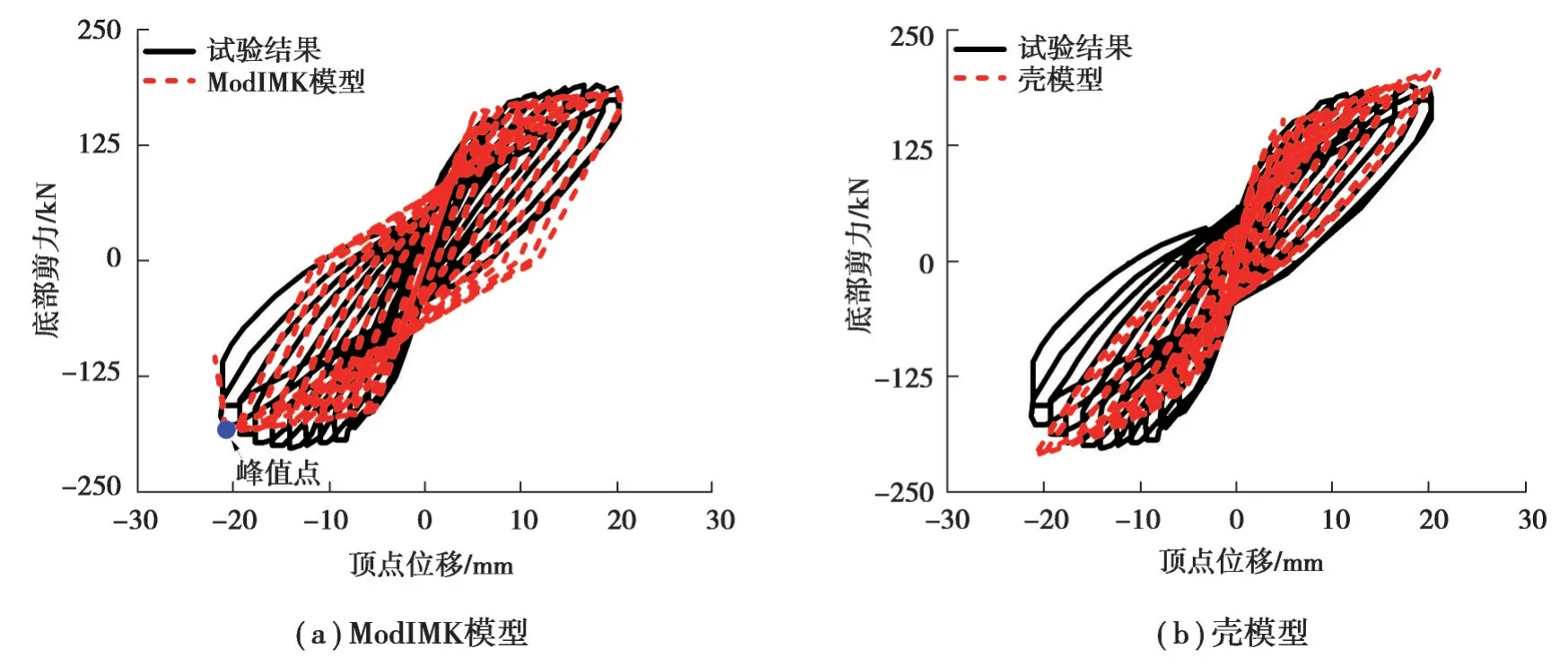
图11 SW1-1试验和模拟结果对比Fig. 11 Comparison of SW1-1 test and simulation results

壳模型模拟结果如图11(b)所示，可以看出壳模型可以精确模拟剪力墙的刚度和承载力，特别是卸载段刚度吻合很好，但达到峰值后没有承载力没有下降趋势，对于破坏和下降段的模拟似乎值得进一步探讨。

4.2 时程分析模拟

为验证文中的剪力墙滞回模型在地震作用下的适用性，选择文献[4]中的5层框架剪力墙进行时程分析模拟。剪力墙每层高3 660 mm，长6 100 mm，厚度为305 mm，一侧边缘约束区配16根直径为36 mm的纵筋，屈服强度为410 MPa，箍筋直径为13 mm，间距为102 mm；混凝土强度为34 MPa；框架跨距为6 100 mm，框架柱为710 mm×710 mm的矩形柱，梁尺寸为460 mm×810 mm。

框架剪力墙的ModIMK模型如图12所示，由于除顶层外每一层剪力墙上下两端都存在弯矩，都有可能进入塑性，需在两端各设一个转动弹簧以模拟其转动，并赋予相同的ModIMK材料本构。需要注意的是，上下两端都设弹簧的情况下，式(3)中系数3应为6，建模时线刚度采用一半层高计算。对于框架梁柱，采用文献[4]中建模方法，框架梁柱采用弹性单元模拟，梁柱结点和支座处的塑性铰区设转动弹簧以模拟其转动，弹簧采用ModIMK材料定义。剪力墙与框架之间采用刚性连接，控制每层框架和剪力墙的水平位移相等。

图12 5层框架剪力墙ModIMK模型Fig. 12 5 storey frame-shear wall ModIMK model

文献[4]采用OpenSees中的弯剪耦合多连杆模型SFI-MVLEM单元模拟剪力墙，框架部分的建模与上文一致。每层剪力墙由2个相同的SFI_MVLEM单元模拟，混凝土采用ConcreteCM材料，Steel02材料模拟钢筋，把钢筋和混凝土赋予FSAM材料定义剪力墙纤维板，并对每个SFI-MVLEM单元设6个纤维板定义剪力墙单元[47]。

SFI-MVLEM和ModIMK模型采用倒三角形加载方式Pushover的结果见图13所示，可以看出2种模型的屈服段比较吻合。SFI-MVLEM随着侧向位移的增加，底部剪力逐渐增加，顶部位移达到1 100 mm时进入下降段，此时顶点位移角达6.1%，这一位移角明显高估了剪力墙的变形能力。ModIMK模型剪力墙发生破坏时的峰值位移为430 mm，转角为2.4%，分析结果更合理，图中剪力墙破坏之后底部剪力还有一定值是因为框架还没破坏。

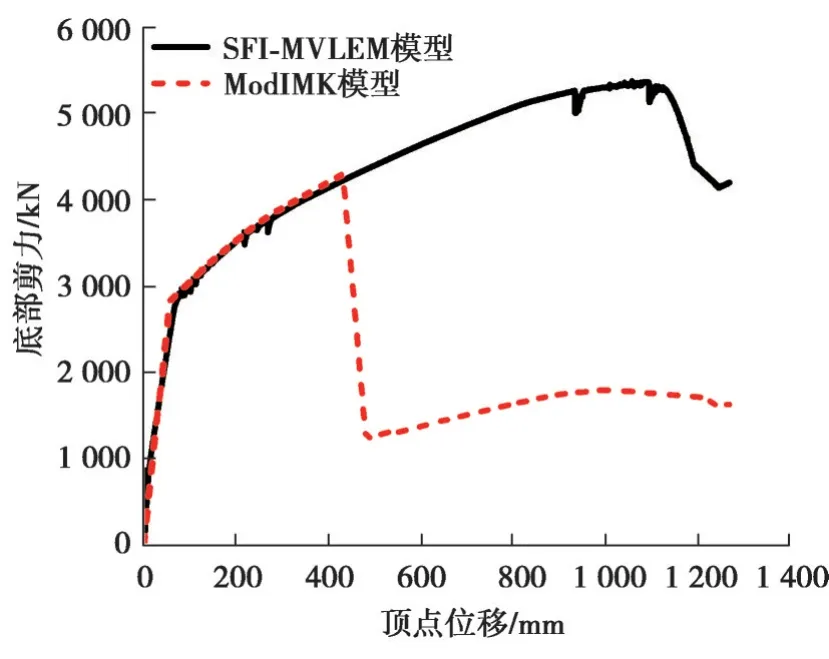
图13 Pushover分析对比Fig. 13 Pushover analysis

文献[4]还用SFI-MVLEM模型进行了时程分析模拟，结果如图14所示，采用同一条波对文中的ModIMK模型进行分析，从图中可以看出2种模型时程分析结果基本吻合，说明ModIMK模型可以和精细有限元一样有效预测框架剪力墙在地震作用下的响应。

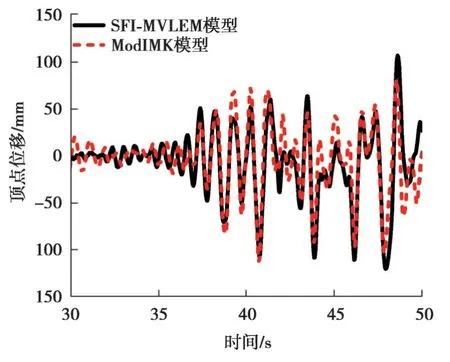
图14 时程分析对比Fig. 14 Time history analysis

4.3 IDA计算

增量动力分析(IDA)可以预测结构在地震作用下的倒塌概率，在太平洋地震工程研究中心(PEER)地震波数据库中下载了13条远场地震波，对文献[48]的8层剪力墙进行增量动力分析，地震波信息见表3所示。剪力墙首层高4 000 mm，其余层高3 600 mm，剪力墙截面长7 000 mm，厚度500 mm，保护层厚度为59 mm，混凝土强度fc=38.8 MPa。两端约束加强区共配32根直径为12.5 mm的纵筋，中间腹板区配有30根直径10 mm的纵筋，纵筋屈服强度fy=567.3 MPa；约束加强区箍筋间距为100 mm，直径为10 mm，屈服强度fv=300 MPa。

表3 13条远场地震波Table 3 13 far-field seismic waves

文献[48]用纤维模型进行了模拟计算，纤维模型钢筋材料采用Steel02模拟，并用Minmax材料包裹来控制钢筋的受压和受拉极限应变，以此定义剪力墙的破坏准则。结构第一周期T1为0.95 s，阻尼比为5%，根据文献[49]，以结构第一周期对应的地震谱加速度Sa(T1,5%)作为地震强度指标IM，以最大层间位移角θmax作为地震响应指标DM，文中分析时IM按0.2g的间隔增加。

图15为2种模型的IDA结果，分析不收敛导致结构变形趋向无限大作为达到倒塌状态。文献[50]建议以5%的位移角作为剪力墙的上限倒塌指标，计算中最大位移角超过5%时，即便计算还能收敛也应视为结构倒塌，因为剪力墙变形位移角基本很难达到5%。图15给出了确定Sa下对应的最大层间位移角的中值曲线(50%分位曲线)。从分析结果对比可以看出2种模型在低IM下DM指标比较吻合，在较高IM下ModIMK模型倒塌点基本在5%左侧，且倒塌位移角均值接近剪力墙的极限转角0.033。纤维模型倒塌点的最大位移角相对较大，中值曲线也验证了这一点，原因主要是纤维模型对于破坏状态的模拟比较复杂，其应变限值受较多的因素影响[50]。

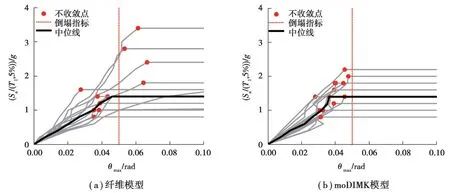
图15 IDA结果Fig. 15 IDA results

在计算过程中ModIMK模型计算收敛性较好、计算速度快，所用的时间大约为精细模型和纤维模型的百分之一左右。

5 结 论

笔者在试验结果和理论分析的基础上，提出了基于ModIMK滞回规则的RC剪力墙弯矩-转角三折线计算模型，通过数值模拟对模型进行验证。

1）通过理论分析与试验总结把剪力墙侧向变形过程分为3段：屈服段、强化段、破坏段，提出了剪力墙的弯矩-转角三折线模型，模型计算简单，便于实际应用。

2）提出了模型关键点计算方法，通过105个试件试验结果分析提出了截面有效刚计算方法，通过对3种计算方法对比发现剪跨比对有效刚度影响明显，尤其在剪跨比小于2.0时有效刚度计算误差稍大，通过对试验数据重新拟合，文中提出的计算方法精度较高。对构件的峰值位移计算进行了研究，当箍筋间距满足一要求时，箍筋用量达到一定量时再增加不能显著增加剪力墙的变形能力。105个剪力墙试件的计算与试验对比结果表明提出的弯矩-转角三折线模型能有效预测剪力墙的非线性变形行为。

3）采用OpenSees中的ModIMK材料定义模型的滞回规则，对剪力墙低周反复试验进行模拟，结果表明剪力墙的ModIMK模型与试验结果吻合很好，验证了模型的准确性；与分层壳模型的对比表明提出模型对剪力墙破坏段的模拟更有优势。5层框架剪力墙的时程分析表明ModIMK模型能有效模拟框架剪力墙在地震作用下的响应。8层剪力墙的增量动力分析(IDA)对比表明ModIMK模型预测的剪力墙倒塌位移角比纤维模型小。