基于3种类型驾驶员变安全距离防夹塞变道的车辆控制策略

蒋 浩, 赵又群, 林 棻, 张雯盺

(南京航空航天大学 能源与动力学院, 江苏 南京 210016)

随着中国汽车保有量的快速增加,驾驶员不良驾驶习惯在交通拥堵中造成了大量的事故[1].特别是夹塞变道所造成的事故,在中国占发生交通事故总数的15.80%[2].进行防夹塞变道研究非常有必要,它不仅可以提高行车安全,还有助于维持正常的车流[3].

很多学者针对防夹塞变道的自车控制策略进行了研究.文献[4]针对自适应巡航控制(adaptive cruise control,ACC)模型的夹塞变道工况,提出了面对他车夹塞变道时通过降低车速来提高安全性的控制策略.文献[5]研究了卡车编队系统遇到他车夹塞变道的工况,提出了卡车之间需要快速增加间隙的控制策略[6].

还有学者针对邻车驾驶员的变道意图预测进行了研究.文献[7]通过实车试验,分析了中国驾驶员在高速公路上的车道变换特性,通过车道变换频率、转向信号使用和后视镜使用的统计数据分析驾驶员的换道意图.文献[8]进行了同样的研究发现他车夹塞变道主要原因是其前车车速慢.

对于夹塞变道行驶下的安全预警,文献[9]提出在该工况下需要考虑纵向安全距离,低速考虑横向距离,高速时考虑他车夹塞角度.文献[10]考虑到驾驶员人格特质对风险驾驶的影响,设计了基于客观指标和驾驶员特征的变道意图预测模型.文献[4]研究了他车在夹塞变道最初的5到10 s内可以通过恒定的速度“拉回”到自己的车道.

目前针对夹塞变道工况的研究中,通过自车预警减速扩大跟车距离,或者对他车变道意图预测,以及对他车驾驶员变道意图预测,都是在后处理夹塞工况.然而对于该工况的前处理,针对改进跟车系统、缩小跟车距离,通过消除他车驾驶员的夹塞意图来防止被夹塞的策略却研究较少.笔者通过研究自车3种类型驾驶员的车头时距和停车间距等特性来改进跟车系统,利用MATLAB/Simulink与CarSim联合仿真平台搭建夹塞变道工况,研究基于变安全距离防夹塞变道车辆控制策略的有效性.

1 驾驶员类型和特性

1.1 驾驶员类型

驾驶员类型由自身的性别、年龄、性格等内在特质决定,它能够反映在一定工况下驾驶员的操纵倾向性.基于车辆状态值,如车速、加速度、油门、刹车和反应时间等的研究[11-12]表明,驾驶员类型的划分多种多样.有的学者将其分为2种:激进型和温和型.有的将其分为3种:冷静型、正常型和激进型.驾驶员类型的划分至多可为18种,逐一研究会成倍增加试验数据,且对于研究的规律性方面没有明显提高.本研究就谨慎、适中和激进的3种类型驾驶员展开研究.

1.2 驾驶员特性

驾驶员特性是基于驾驶员类型更进一步的具体化,是驾驶员类型具体的体现.驾驶员跟车特性如表1所示[7].一方面为停车间距,谨慎的驾驶员会留出更多的停车间距,适中的驾驶员会留出中等的停车间距,激进的驾驶员留出的停车间距最小;另一方面为车头时距,它主要是为了表征在前车车速突然变为0的情况下,自车以当前车速行驶与前车相碰撞的时间,通过相对距离除以自车速度计算得到.显然,谨慎的驾驶员车头时距更大,激进的驾驶员车头时距更小.

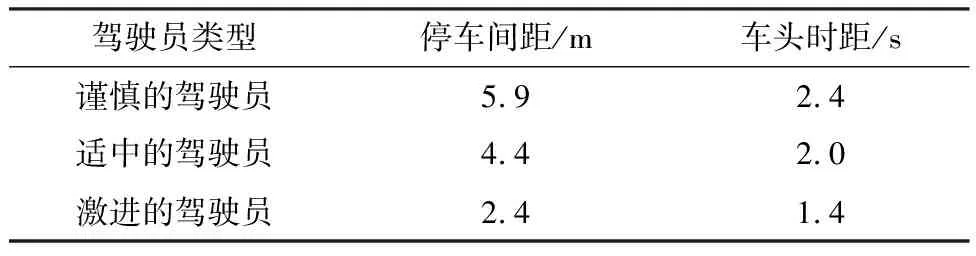
表1 驾驶员的跟车特性

2 基于驾驶员特性的安全距离模型

2.1 传统的安全距离模型

固定安全距离模型是指当跟车间距小于安全距离时产生的主动预警或者制动.该模型的优点在于使用方便,不足之处在于对该固定值的选取没有理论支持,以及该模型对环境变化的适应性比较差.该模型的表达式为

s0=ds,

(1)

式中:s0为跟车安全距离;ds为设定的固定距离安全值.

恒定车头时距模型主要考虑了恒定车间距离和自车车速.随着自车车速的提高,安全距离也变大.该模型主要用于自车与前车相对速度并不大的情况,计算公式如下:

s0=v0tc+dc,

(2)

式中:v0为当前车速;tc为恒定车头时距,一般取1.5～2.8 s;dc为恒定车间距离,取4～6 m.

可变安全距离模型是基于固定车头时距模型提出来的,将车间距离定义为一个可变量,计算公式如下:

s0=v0tv+dc,

(3)

tv=tv1+tv2,

(4)

式中:tv1和tv2为大于0的常数,它们根据自车以及前车状态进行实时调节.

前车匀速工况下,驾驶员制动距离模型通过车辆的制动距离来计算安全距离,计算公式如下:

(5)

式中:Δv为自车与前车的相对速度;tp为驾驶员反应时间和制动器反应时间之和;μ为道路路面附着系数,干燥路面μ=0.85;g为重力加速度,g=9.8 m/s2.

2.2 基于驾驶员特性的跟车安全距离模型

以上传统的安全距离模型建立的侧重点是基于车辆当前状态产生的直接影响,它们存在一定的局限性.车辆状态改变的根本原因是驾驶员的操纵特性.将驾驶员特性融入到安全距离模型中,能更加全面地描述跟车安全距离模型,有利于提高行车的舒适性以及驾驶员对控制系统的接纳程度.

综合考虑表1中驾驶员的2种跟车特性,设计安全距离模型如下:

(6)

式中:th为车头时距;d0为停车间距.

由式(6)可知,安全距离与自车车速、停车间距成正比,当前车加速时或者自车减速时,相对速度变大,使安全距离小于当前距离,表示驾驶员可以加速;当前车减速时或者自车加速时,相对速度变小甚至为负值,使安全距离大于当前距离,表示驾驶员应该减速.相比于传统的安全距离模型,该模型充分考虑了驾驶员特性、相对速度对跟车安全距离的影响,又可以实现根据驾驶员类型进行调节,使安全模型更加个性化,保证行驶安全.

在MATLAB/Simulink软件中搭建的安全距离模型离散,需要将式(6)离散化,可得

s0=v0th-Δvτ+d0,

(7)

式中:τ为积分间隔时间,由于ACC工况中相对速度变化较慢,取2 s.

在匀速跟车时,Δv为0,防夹塞安全距离模型可表示为

s0=v0th+d0.

(8)

2.3 基于驾驶员特性的防夹塞安全距离模型

根据研究的工况,当遇到他车夹塞变道时,通过转换跟车安全距离模型为防夹塞安全距离模型,缩小跟车距离来防止被夹塞.考虑3种类型驾驶员特性,结合式(5)建立在前车匀速工况下,基于车头时距、制动距离和停车间距的防夹塞安全距离模型如下:

(9)

式中:t1为系统反应时间和液压系统起作用的时间之和,取1 s.

从式(9)可以看出:防夹塞安全距离同驾驶员停车间距成正比,与自车速成正比,与相对速度的平方成反比.

在匀速跟车时,相对速度几乎为0,此时的防夹塞安全距离模型可表示为

s0=v0t1+d0.

(10)

3 仿真试验工况搭建

3.1 基于Sigmoid函数的变安全距离车速控制器

在匀速跟车行驶工况中,自车通过相对速度、相对距离进行直接反馈,控制油门或者刹车的基本逻辑如下:当速度差为正、相对距离变大时,进行加速;速度差为负、相对距离变小时,进行减速;刹车和油门不能同时作用.由于操控加减油门和刹车挡板是一个平缓的过程,所以需要对它们的控制输入信号进行平滑处理.

使用Sigmoid函数来规范控制输入量,函数曲线如图1所示.对于基于安全距离的控制量,控制逻辑如下:速度差越大,油门也就越大;速度差越小,油门也就越小;速度差为0时,油门也基本为0,最后实现匀速跟车.对Sigmoid函数进行改进,为了满足基于安全距离的控制逻辑,在原有函数的基础上,将其向右平移3个或5个单位长度.

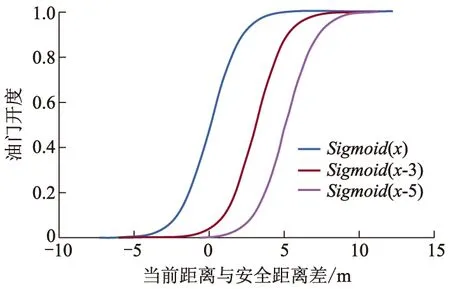
图1 Sigmoid函数及改进

基于此油门调节器,设置仿真验证工况:前车车速为10 m/s,自车车速起始为0,前后两车相距10 m,雷达检测距离为100 m.跟车仿真如图2所示,当Sigmoid函数向右平移3个基本单位长度时,油门控制调节器的跟车效果最好,第3秒开始保持了稳定的跟车距离.而平移的距离过多会使油门开度过大引起两车相碰,反之油门开度过小,使跟车距离被拉大.

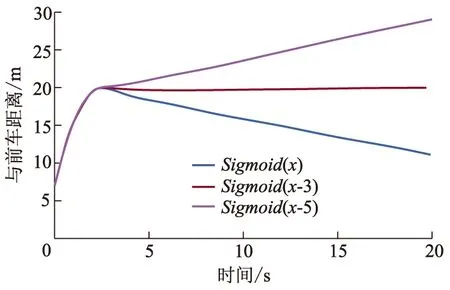
图2 基于Sigmoid函数的油门调节器

3.2 MATLAB/Simulink与CarSim联合仿真模型

MATLAB/Simulink与CarSim联合仿真搭建的模型如图3所示,通过直接反馈控制,将CarSim模型中毫米波雷达测得的相对距离dr和相对速度输出到控制算法中,结合安全距离模型以及驾驶员特性,求解出汽车油门开度以及制动信号的控制量,并输出到CarSim中.

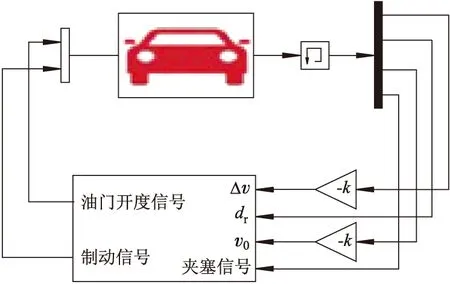
图3 CarSim/Simulink联合仿真模型

将夹塞车信号输出用于安全距离模型的选择,前车相对速度和距离输入到安全距离模型中,再将输出的理论跟车安全距离同当前距离比较,做出加速或者制动的控制策略.加速情况下,距离差值会输入到Sigmoid函数中,将输出一个油门开度给发动机;制动时,将误差信号反馈给制动主缸.

夹塞信号的判断逻辑为他车侧向位移是否从-6.0 m运动到大于-5.5 m,如果是,则切换成防夹塞安全距离模型.在他车逐渐离开返回原始车道过程中,如果侧向位移从大于-5.5 m到小于-5.5 m,则从防夹塞安全距离切换回跟车安全距离.

3.3 仿真试验工况设置

为了研究夹塞变道工况,在CarSim中设置一条单向双车道的干燥道路(μ=0.85),自车与前车匀速行驶于左侧车道,如图4所示.

图4 夹塞变道CarSim模型

预先设置一辆夹塞车,以相同车速按图5所示的侧向运动轨迹驶向自车所在车道.车速为10 m/s工况下,他车从4 s开始夹塞,4 s到7 s向自车所在车道移动,从-6 m到-3 m的侧向位置,其侧向移动速度为1 m/s;7 s到9 s不再移动;9 s到12 s,从-3 m到-6 m,移回了原来车道.

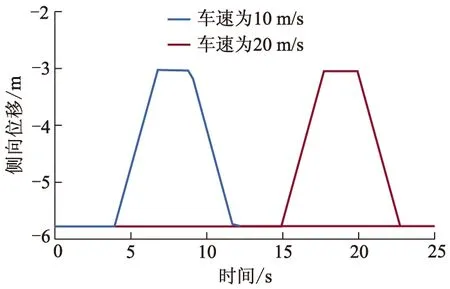
图5 夹塞车运动轨迹设置

夹塞车所处的车道中心线是相对于自车车道,自车车道中心线的横向位置坐标为0.在CarSim软件中,该轨迹的计算语句为

-5.75+GT(ts,3)(tq-3,2.75)-
GT(ts,8)(tq-8,2.75),

(11)

式中:ts为夹塞时间;GT(ts,3)为他车从仿真开始第3 s开始夹塞的速度函数,其他类同;tq为仿真时间.

20 m/s工况下,在CarSim软件中,他车夹塞运动轨迹的计算语句为

-5.75+GT(ts,14)(tq-14,2.75)-
GT(ts,19)(tq-19,2.75).

(12)

设置2个毫米波雷达,一个置于右后视镜处用于检测夹塞车辆的夹塞角度和速度;另一个置于前挡风玻璃中部,用于检测前方车辆的速度和距离.

3.4 防夹塞变道距离约束

自车驾驶员在跟车行驶时通常需要考虑如下2个要素:与前车的安全距离以及他车夹塞变道的概率.研究发现,他车的切入概率随着自车跟随间隙变大而增加,验证了车辆的成功夹塞需要较长的跟车间隙.因此,可以通过控制缩小自车的跟车距离来防止被夹塞.将夹塞变道的纵向距离约束等同于单移线变道的纵向距离约束,单移线变道所需要的最短距离sy如表2所示.

表2 夹塞变道所需的纵向距离约束

通过线性插值可得

sy=3.821v0+0.218.

(13)

由式(13)可知:当车速为10 m/s时,夹塞变道所需要的最小距离为38.4 m;当车速为20 m/s时,夹塞变道所需要的最小距离为76.6 m.

夹塞变道下,夹塞车进入自车所在车道,完成并道所需要的纵向距离是单移线变道距离L的1/2,如图6所示,车速为10 m/s时,L/2=19.2 m;车速为20 m/s时,L/2=38.3 m.该距离将作为判断在匀速跟车时,防他车夹塞变道的距离约束.

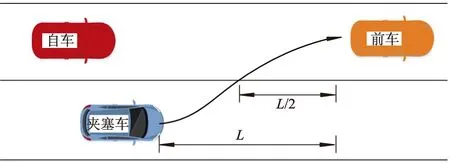
图6 夹塞变道的距离约束

4 仿真试验与评价

4.1 车速为10 m/s时的仿真分析

设置夹塞变道仿真工况:前车车速为10 m/s,初始距离为10 m.基于3种类型驾驶员的变安全距离防夹塞变道仿真试验结果如下:自车与前车距离变化曲线如图7所示,自车速度变化曲线如图8所示,自车油门开度变化曲线如图9所示,自车制动主缸压力变化曲线如图10所示.

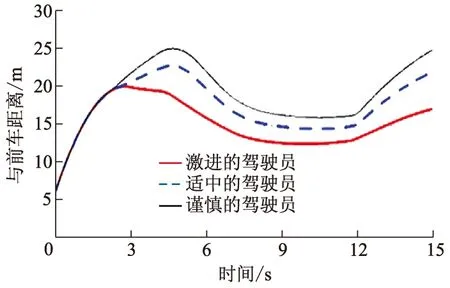
图7 自车与前车距离变化曲线

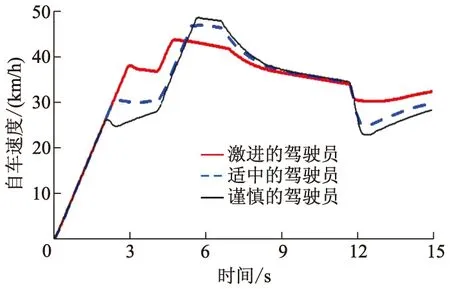
图8 自车速度变化曲线

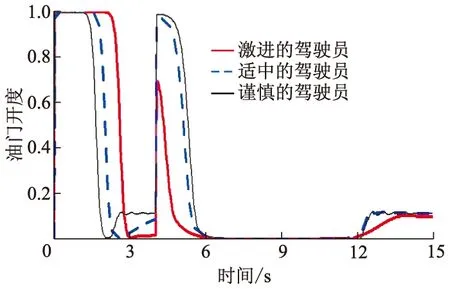
图9 自车油门开度变化曲线

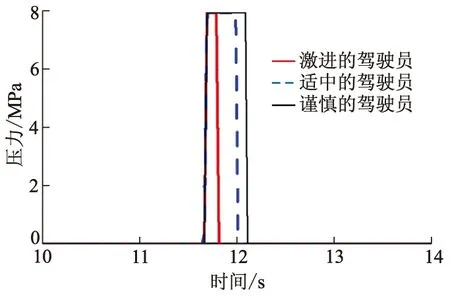
图10 自车制动主缸压力变化曲线

从图7-10可以看出,自车经历了2个加速阶段、2个匀速阶段和1个减速阶段.分析如下: ① 时间为0～3 s,自车加速跟上前车;② 时间为3～4 s,自车没有检测到夹塞车辆,以跟车安全距离模型匀速跟车,具体体现在跟车距离几乎没有变化,而谨慎的驾驶员跟车距离还未进入加速阶段,就检测到了夹塞车辆;③ 时间为4～8 s,自车检测到夹塞车辆,跟车安全距离模型切换为防夹塞安全距离模型,加速跟车,缩小与前车距离;④ 时间为8～12 s,自车匀速跟车,3种类型驾驶员均根据防夹塞安全距离跟车行驶;⑤ 时间为12～15 s,自车不再检测到夹塞车,防夹塞安全距离模型切换为跟车安全距离模型跟车,在12 s左右,自车短暂制动,这是由于模式切换造成的.

单独分析②和④2个匀速阶段,结果如表3所示,其中夹塞变道距离由式(13)计算得到.从表3可以看出,实际值和理论值误差不大,证明了基于Sigmoid函数设计的车速控制器的准确性.与他车夹塞变道需要的纵向距离相比,采用跟车安全距离模型,只有激进的驾驶员不会被夹塞;采用改进后的防夹塞安全距离模型表明,3种类型驾驶员均不会被夹塞,验证了变安全距离防夹塞变道的控制策略的有效性.

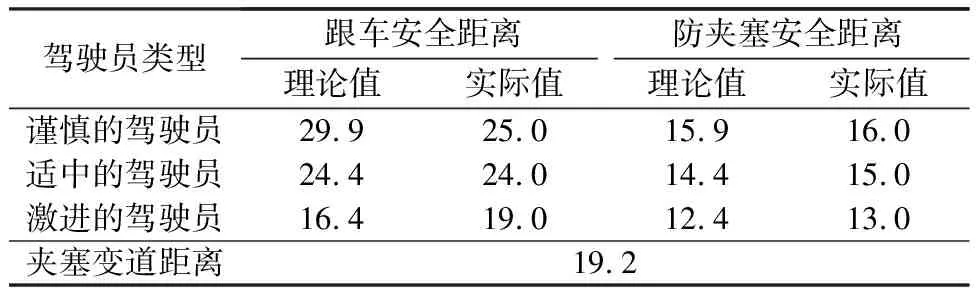
表3 车速为10 m/s的仿真结果 m

4.2 车速为20 m/s时的仿真分析

设置夹塞变道仿真工况:前车车速为20 m/s,初始距离为0.基于3种类型驾驶员的变安全距离防夹塞变道仿真试验结果如下:自车与前车距离变化曲线如图11所示,自车速度变化曲线如图12所示,自车油门开度变化曲线如图13所示,自车制动主缸压力变化曲线如图14所示.

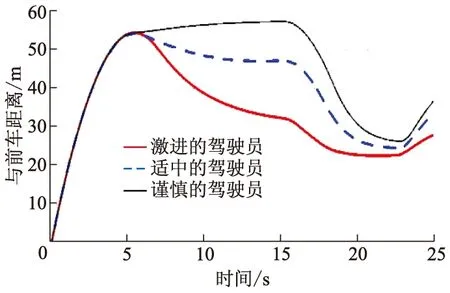
图11 自车与前车距离变化曲线

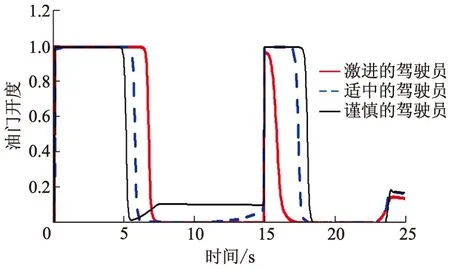
图13 自车油门开度变化曲线

从图11-14可以看出,自车经历了2个加速阶段、2个匀速阶段和1个减速阶段. 分析如下: ① 时间为0～7 s,自车加速跟上前车;② 时间为7～15 s,自车没有检测到夹塞车辆,以跟车安全距离模型匀速跟车,具体体现在跟车距离几乎没有变化;③ 时间为15～18 s,自车检测到夹塞车辆,跟车安全距离模型切换为防夹塞安全距离模型,加速跟车,缩小与前车距离;④ 时间为18～23 s,自车匀速跟车,3种类型驾驶员均根据防夹塞安全距离跟车行驶;⑤ 时间为23～25 s,自车不再检测到夹塞车,防夹塞安全距离模型切换为跟车安全距离模型跟车,在23 s,自车短暂制动,这是由于模式切换造成的.

单独分析②和④2个匀速阶段,结果如表4所示,实际值和理论值误差不大,证明了基于Sigmoid函数设计的车速控制器的准确性.与他车夹塞变道需要的纵向距离相比,采用跟车安全距离模型,只有激进的驾驶员不会被夹塞;采用改进后的防夹塞安全距离模型,3种类型驾驶员均不会被夹塞,验证了变安全距离防夹塞变道控制策略的有效性.

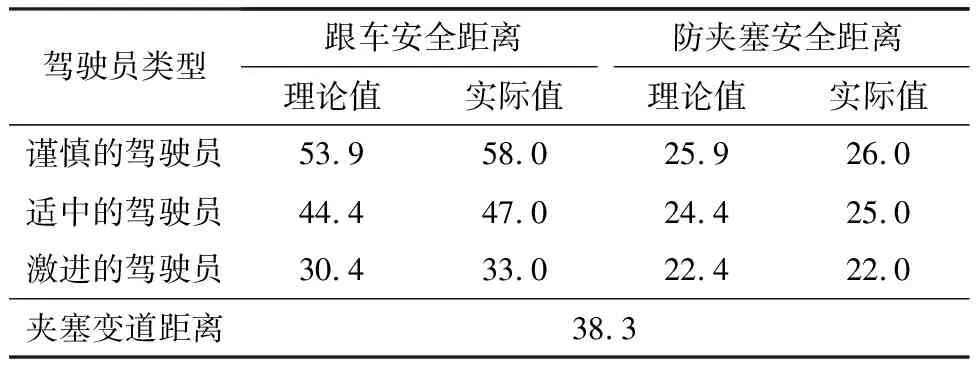
表4 车速为20 m/s的仿真结果 m

5 结 论

1) 在传统安全距离模型的基础上,考虑自车的车头时距、停车间距等跟车特性,建立了基于谨慎、适中和激进的3种类型驾驶员跟车安全距离模型和防夹塞安全距离模型.通过Sigmoid函数建立了变安全距离的车速控制器.检测到他车夹塞变道,选择防夹塞安全距离模型;无夹塞车辆,选择跟车安全距离模型.

2) 在车速分别为10、20 m/s时,利用MATLAB/Simulink与CarSim联合仿真平台进行试验,验证了基于变安全距离防夹塞变道车辆控制策略的有效性,为近距离跟车防夹塞车辆控制策略提供了参考.