基于EEMD-MFDFA的镇江港PM2.5演化特征分析

郑敏学, 毛 静, 孙智灏, 朱 龙, 李志坚, 居 珍, 黄爱国

(1. 江苏大学 安全与环境工程学院, 江苏 镇江 212013; 2. 镇江港务集团有限公司, 江苏 镇江 212001)

镇江港地处江苏省镇江市西部,是长江三角洲地区重要的对外开放港口,港口地理坐标为北纬32°11′10.25′′～32°11′27.25′′,东经119°37′56.53′′～119°40′16.20′′,2020年上半年货物吞吐量达17 305万t,跻身全国前十[1].港口在散货作业、场地堆存及车辆运输中所产生的PM2.5是构成区域大气污染的主要因素.随着港口铁矿石、煤炭等易起尘散货吞吐量的快速增长,PM2.5污染的控制难度进一步加大,极大影响职工健康、港区工作环境及周边生态环境的安全[2].中共中央、国务院2021年印发的《国家综合立体交通网规划纲要》提出,要建立绿色化水平居于世界前列的国家综合立体交通网,港口作为交通网的重要组成部分,必须全面提升PM2.5治理水平,构建现代化绿色港口.镇江港共有15个监测点,分布密度高,覆盖各个生产场所,可以充分反映港口PM2.5的分布特点.研究镇江港的PM2.5分布规律及其演化特征,分析港口污染形成的机制,对提高PM2.5治理水平具有重要参考意义.

PM2.5的演化过程既受人为、气象等因素的影响,同时也受到大气化学反应等机制作用的影响,因此PM2.5演化具有非线性、非平稳性等复杂特征.目前传统数理方法无法消除非平稳时间序列内在的自相关性和识别外在趋势所导致的伪相关现象[3].多重分形去趋势波动分析(MFDFA)方法可直接从非线性复杂系统入手,整体上定量描述系统演化过程,获取其内在的变化规律[4].然而MFDFA算法的去趋势部分仍然存在不足,当序列太长或其趋势不符合多项式类型时,分析结果会不准确.为了克服该方法的不足,文献[5]将经验模态分解(EMD)算法作为去趋势模块嵌入到MFDFA算法当中,EMD在时间序列数据处理方面具有明显优势,但也存在“模态混合”的问题,即在不同时间尺度的信号可能被归类成同一个固有模态函数(IMF),或相同时间尺度的信号可能被归类成不同IMF.为了克服上述缺点,文献[6]提出了集合经验模态分解(EEMD)算法,该算法可以更准确表示变量趋势.目前基于EEMD的MFDFA算法已用于数字高程模型和降水动力学等方面的研究[7-8].

为了探讨镇江港PM2.5浓度的演化特征,首次采用EEMD-MFDFA算法,分析港口PM2.5时间序列的多重分形特性,并基于自组织临界(SOC)理论,阐明港口不同监测点粉尘排放对PM2.5的非线性动力学影响,将为港口PM2.5治理提供科学依据.

1 数据与方法

1.1 研究数据来源

研究中所运用的PM2.5时均浓度数据均采自2019—2020年镇江港的15个空气质量自动监测点.监测原理为光散射法,共收集数据为206 245组,经审查核验,其中有效数据为205 667组.2019—2020年镇江港PM2.5时均浓度ρ(PM2.5)监测点及空间分布如图1所示.

图1 2019—2020年PM2.5时均浓度监测点及空间分布

1.2 基于EEMD的MFDFA算法

1.2.1MFDFA算法

根据文献[9],MFDFA算法包括5个步骤.

1) 运用具有时间序列特征的数据xk(k=1,2,…,N)构建新的序列Y(i),i为时间序列特征数据中的第i个数据,即

(1)

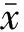
2) 将序列Y(i)分成Ns个独立子序列,s为时间尺度.为了避免尾部数据的丢失,对其进行逆向处理,得到2Ns个独立子序列.

3) 对每个子序列通过最小二乘法得到局部协方差函数F2(v,s),即当v=1,2,…,Ns时,

(2)

当v=Ns+1,Ns+2,…,2Ns时,

(3)

式中:yv(i)为第v段数据上的第i点对应的趋势函数.

4) 所有2Ns个独立子序列的q阶波动函数通过以下等式获得:

(4)

5) 广义Hurst指数h(q)可通过计算函数Fq(s)与时间尺度s的双对数曲线斜率得到.通过Legendre变换,可得到奇异指数α、多重分形谱函数f(α)和广义Hurst指数h(q).三者关系如下:

α=h(q)+qh(q),

(5)

f(α)=q(α-h(q))+1.

(6)

对于单分形时间序列,h(q)独立于q;对于多重分形时间序列,h(q)随q的变化而变化.h(2)>0.5,表明时间序列存在长期记忆性,且具有正效应,数值越大,表示持续性越强.Δα=αmax-αmin为多重分形谱宽度,该值越大,多重分形特征越强,数据波动越剧烈[10].Δf(α)=f(αmin)-f(αmax)为最小概率子集和最大概率子集的分形维数之差.Δf(α)<0表示PM2.5浓度位于较低值的概率大于位于较高值的概率.

1.2.2EEMD算法

EEMD算法本质是一种使用正态分布的白噪声序列辅助数据分析方法[11-12].根据文献[13], EEMD算法包括3个步骤.

1) 将正态分布的白噪声序列nm(t)添加到原始系列x(t)中,第m次加入白噪声序列后函数为

xm(t)=x(t)+nm(t).

(7)

2) 使用EMD方法将加入白噪声序列的信号分解为K个固有模态函数IMF分量Cmj(t)和残差r(t).

3) 在重复上述步骤过程中加入不同的白噪声序列.加入白噪声信号的次数为100次,白噪声序列等级为0.2级,可获得较好的分解效果[14-15],最终获得分解的相应IMF分量和残差.将分解得的IMF集合取平均值,用以抵消白噪声序列,得到EEMD分解后的IMF分量和残差如下:

(8)

式中:K为加入高斯白噪声的总体数量;m为添加白噪声的次数;j为对原序列进行EEMD分解得到的第j个分量;cmj(t)和rm(t)分别为第m次分解得到的第j个IMF分量及其对应的剩余残差分量;cj(t)为进行第K次分解得到的第j个IMF分量;r(t)为最后得到的残差.

1.2.3基于EEMD的MFDFA算法

为了优化传统MFDFA算法中的去趋势问题,将EEMD算法嵌入MFDFA算法的第3步,用残差替代原始序列,保持其他步骤不变[16].在EEMD-MFDFA算法中,第3步表述如下:

当v=1,2,…,Ns时,

(9)

当v=Ns+1,Ns+2,…,2Ns时,

(10)

1.3 自组织临界理论

自组织临界理论可以阐释复杂系统中宏观方面出现幂律分布特征的动力机制,临界状态下的大气系统相对稳定,微小的干扰可能会导致连锁反应,使系统发生“崩塌”.系统达到自组织临界状态的最显著表征之一是幂律分布特征.若PM2.5时均浓度时间序列波动具有自临界组织特性,需满足以下关系式[17]:

lg[M(Δρ≥Δρ0)]∝-λlg Δρ,

(11)

式中:ρ为某时刻n的PM2.5时均浓度;Δρ为PM2.5时均浓度的波动值,Δρ=ρn+1-ρn;λ为标度指数;M为PM2.5时均浓度波动值大于某一个PM2.5时均浓度波动值Δρ0的次数.

2 结果与分析

2.1 空间分布特征

图1中,临江区域总体PM2.5时均浓度(58.57 μg/m3)高于非临江区域PM2.5时均浓度(52.67 μg/m3).港口原始PM2.5时均浓度变化范围为10.0～223.9 μg/m3.依据GB 3095—2012《环境空气质量标准》,研究期间有18%的日均浓度超过国家二级标准,空气质量等级为轻度污染及以上.14号监测点浓度较高,日均浓度为62.92 μg/m3,10号监测点浓度偏低,日均浓度为40.97 μg/m3,最大浓度差为21.95 μg/m3.14号监测点位于集装箱作业区域与码头生产区域运输线交汇点,在集装箱运输、码头货物作业时车辆来往频繁,产生了包含作业扬尘、道路扬尘及车辆尾气等多种尘源,从而造成PM2.5浓度持续偏高.10号监测点靠近办公区,远离生产作业区域,因而PM2.5浓度偏低.

2.2 基于EEMD-MFDFA算法的分析

对15个监测点在2020年的PM2.5日均浓度数据分别进行了EEMD分解,发现12个监测点数据序列长度均为366个,其余3个监测点数据序列长度不足366个.为了保持PM2.5日均浓度数据连续性,研究中仅对序列长度为366个的12个监测点PM2.5日均浓度数据进行分析.12个监测点分布均匀,涵盖了整个港口,对其PM2.5日均浓度数据进行多重分形分析可以反映港口PM2.5日均浓度演化特征.1号监测点PM2.5日均浓度处于12个监测点的中位(排序为第7).以1号监测点PM2.5日均浓度为例,计算得到的IMF分量和残差r(t)结果如图2所示,其中加入白噪声次数为100次,白噪声序列等级为0.2级.通过图2中的残差曲线,可以清晰地了解原始数据的总体变化趋势.

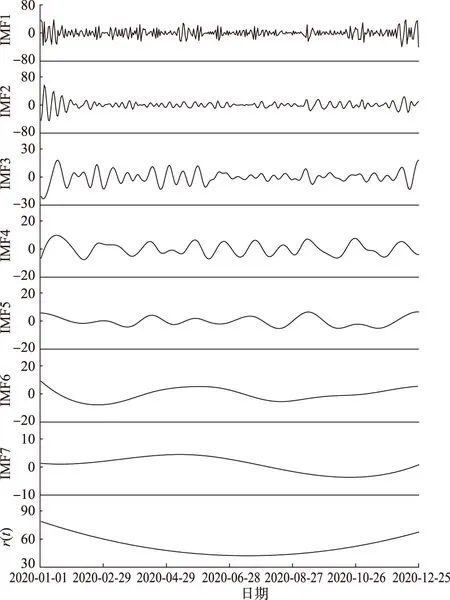
图2 1号监测点PM2.5日均浓度的EEMD分解结果

图3为通过对2020年镇江港12个监测点PM2.5日均浓度数据进行分解得到的残差曲线.由图3可知:港口总体PM2.5浓度变化呈U形分布;1月和12月PM2.5浓度较高,6—9月PM2.5浓度偏低,7月PM2.5浓度最低.

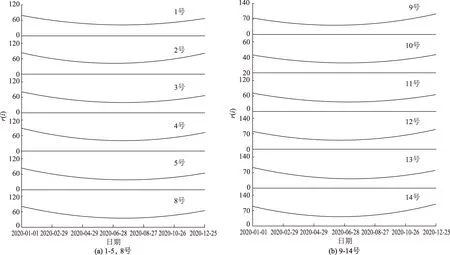
图3 12个监测点PM2.5日均浓度数据的残差曲线

温度是影响PM2.5浓度变化的重要因素之一.通过Pearson相关分析方法,计算并统计各监测点PM2.5时均浓度与温度的相关系数,发现PM2.5时均浓度与温度呈负相关的关系,相关系数为-0.482～-0.113.这是因为高温时有较强的气流活动,有利于污染物扩散.同时,镇江6—9月气温高、降水多,而1月和12月气温低、降水少,温度、降雨等是导致港口PM2.5浓度序列的残差曲线呈U形变化的重要因素.

运用EEMD-MFDFA算法,对港口12个监测点PM2.5浓度进行多重分形分析,得到图4所示的Hurst指数图.

图4 Hurst指数图

由图4可知,各监测点的h(q)随着阶数q值的增大而减小,这表明PM2.5浓度时间序列有多重分形特征.各监测点的h(2)均显著大于0.5,表明PM2.5日均浓度波动不服从经典马尔可夫函数的随机行为,具有显著的长期持续性.即过去排放的PM2.5浓度会对未来的PM2.5浓度造成影响.2、9和14号监测点的h(2)相对较大,分别为2.31、2.30和2.31,说明这3个监测点所在区域的PM2.5浓度长期持续性较高.镇江港位于长江边,三面建有围墙与防风网,风速多为3级及以下,3、4和5级风的PM2.5时均浓度数据分别为总监测数据的99.76%、0.20%和0.04%,不利于粉尘向外部扩散,港口区域处于半封闭状态,半封闭状态会加剧PM2.5浓度长期持续性不变.

PM2.5日均浓度的多重分形谱f(α)和奇异指数α的关系曲线如图5所示.由图5可知:所有监测点的多重分形谱f(α)-α曲线都不对称,都呈现右偏抛物线形状;f(α)<0时,表明镇江港PM2.5浓度在较低水平上波动的概率占主导地位.曲线具有明显的右截断和左长尾,归因于时间序列对大幅度局部浓度波动的敏感性.多重分形谱分析表明,大波动的影响在PM2.5日均浓度时间序列中起主导作用.

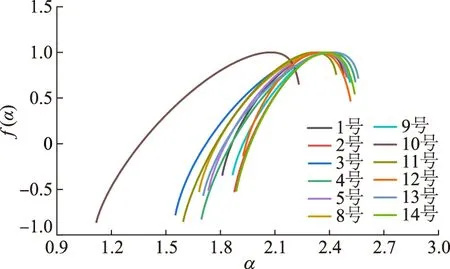
图5 PM2.5日均浓度多重分形谱和奇异指数的关系曲线

由图5还可知:Δα变化范围为0.59～1.11;3、10和13号监测点α相对较大,分别为0.96、1.11和0.85,说明这3个监测点所在区域PM2.5多重分形谱演化出较高波动性;2、12和14号监测点Δα相对较小,分别为0.61、0.59和0.65,反映这3个监测点所在区域PM2.5多重分形谱演化波动性较小.

对比不同监测点的多重分形计算结果可知:3号和13号监测点位于堆场附近,装卸作业和转运作业多,PM2.5浓度多重分形特征较强,受作业时段影响,波动性较剧烈;10号监测点位于门口与办公区域,远离作业场所,主要排放源为汽车扬尘和尾气,多重分形特征较强,对于这些区域的PM2.5污染应侧重即时性防治;2、9和14号监测点靠近作业区及主要输运道路,生产作业及运输过程中的作业扬尘、道路扬尘和柴油车尾气是增大PM2.5浓度的重要因素,特别是频繁来往的集装箱作业车辆和散货转运车辆,造成该区域PM2.5浓度有较强的持续性,多重分形特征较弱,波动性较稳定,对于这些区域的PM2.5污染应侧重于长期性、全时段的防治.

2.3 自组织临界性

为了进一步认识港口PM2.5时均浓度演化的动力机制,计算各监测点PM2.5浓度波动的累积频度统计分布,利用最小二乘法对PM2.5浓度进行线性回归,得到各监测点标度指数.图6为各监测点PM2.5时均浓度波动值的累积分布.由图6可知,各个监测点PM2.5时均浓度的标度指数(即图6中曲线斜率)范围为2.19～3.05,拟合优度R2均达到0.99,证明拟合程度较好,15个监测点的PM2.5浓度均符合幂律分布关系,变化趋势总体相同,可判断港口PM2.5系统为自组织临界系统.由于各个监测点所处区域的主要尘源和环境不同,导致不同区域PM2.5的幂律分布规律略有不同.

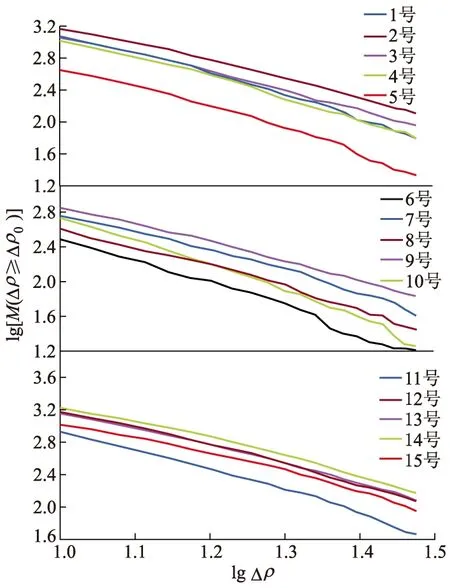
图6 各监测点PM2.5时均浓度波动值的累积分布

由于港口各监测点PM2.5日均浓度均呈现长期持续性发展,未来的PM2.5浓度受过去排放的影响,港口生产作业和货物运输产生的粉尘浓度会进一步累积,易在局部空间内形成较严重的污染事件.若浓度持续增加,系统达到临界状态,少量的PM2.5排放就会形成严重污染事件.港口各区域PM2.5浓度呈现幂律分布结构,是判断具有SOC特征的重要依据.因此自组织临界性是港口PM2.5演化的动力学机制之一,会导致港口未来发生高浓度污染事件的发生.3、10和13号监测点PM2.5浓度波动性大,即时性的排放较频繁.而2、9和14号监测点PM2.5浓度呈长期持续性增强状态,预示未来PM2.5浓度将维持在较高浓度.大波动性与强持续性都会打破港口PM2.5的临界状态,因此加强局部高风险区域粉尘管理,有利于维持整个系统的平衡与稳定.

通过对空间分布和多重分形特征的分析,辨识出港口内2、3、9、10、13和14号等6个高风险区域.对于2、9和14号监测点所在区域应加强道路管理,减少车流量,积极推广使用国Ⅵ排放标准的柴油,确保道路清扫工作规范化,要求车辆加装催化型颗粒物捕集器.增加3、10和13号监测点所在区域的绿化系数,可有效降尘.在3号和13号监测点附近的装卸作业中,应降低落差高度,在落料处增设除尘设施,为降低散货物料运输过程中的PM2.5污染,转运过程宜采用密闭输送.

3 结 论

1) 各监测点的PM2.5日均浓度均具有长期持续性和多重分形特征,过去产生的PM2.5会影响未来一段时间的PM2.5浓度.作业扬尘、道路扬尘和柴油车尾气是导致PM2.5浓度长期持续性增强的主要因素,因此应注重污染的长期性防治.堆场装卸作业、物料转运作业和车辆行驶中产生的扬尘以及汽车尾气导致PM2.5日均浓度波动性增大,应注重即时性防治.

2) 多重分形全面地描述了港口PM2.5系统的复杂动态特性,基于EEMD的MFDFA算法表现出优越的性能,多重分形谱参数(Δα、h(q)和Δf(α))可作为定量评价区域PM2.5浓度演化的指标.

3) 镇江港三面建有围墙与防风网,具有半封闭性,风速多为3级及以下(PM2.5时均浓度数据占比为99.76%).港口PM2.5系统已经达到自组织临界状态,存在发生大气高污染的风险,生产作业中局部微小的PM2.5污染会通过SOC机制形成较大污染.因此,加强局部高风险区域粉尘管理,有利于维持整个系统的平衡与稳定.