分布式电驱动装载机驱动防滑控制*

严周栋，杭 鹏，陈重璞，乔依然，薛 卡，陈辛波，4

（1.同济大学汽车学院，上海 201804；2.同济大学交通运输工程学院，上海 201804；3.江苏汇智高端工程机械创新中心有限公司，徐州 221000；4.同济大学新能源汽车工程中心，上海 201804）

前言

驱动防滑控制是分布式驱动车辆底盘控制的重要组成部分。目前关于驱动防滑控制方面的研究大多基于滑转率［1］，在滑转率可以准确获取的条件下不同学者提出了模糊控制［2］、滑模控制［3］、模型预测控制［4］等方法。为获得最优滑转率、发挥最大路面附着力，基于路面识别［5］、轮胎模型辨识［6］等方法也被提出。

装载机行驶的工况普遍比较复杂恶劣，路面附着系数变化大，工作和行驶过程中前后载荷变化剧烈，铲掘时甚至可以出现车轮腾空。四轮驱动没有从动轮且行驶车速低，铲掘时车速几乎为零，车速估计困难［7］，滑转率计算不准确且变化剧烈。基于滑转率闭环控制的驱动防滑控制方法难以应用［8］。此外相较于传统发动机，电机的速度特性更宽［9］，尤其是当载荷转移较大甚至出现车轮悬空时电机转速会快速上升。持续的滑转可能加剧轮胎的磨损，滑转时将车轮底部土壤卷走改变垂向载荷分布［10］，卷起的土块石粒还容易击打装载机引起破坏和危险。

针对低速等情形下车速和滑转率难以准确计算等问题，Ding等［11］提出了自适应最大转矩控制方法，该方法用均值滤波后的车轮角加速度直接进行补偿。郭存涵等［12］设计滑转率观测器，间接使用滑转率进行防滑控制。Hori 等［13］基于“UOT”电动车设计了模型跟随控制器（MFC）进行防滑控制。通过建立整车和轮胎模型得到参考轮速，反馈控制实际轮速防止车轮打滑。但参考模型会逐渐偏离实际［14］，其又通过反馈车轮转矩、滑转率等进行补偿［15］。然而上述方法均需要准确可靠的车辆动力学模型，相较于公路车辆，装载机工作和行驶工况同时存在，受力情况复杂且变化剧烈，因此上述方法在装载机防滑控制上效果较差。

一些学者从车轮角加速度入手进行防滑控制。Zirek 等［16］通过轨道车辆台架试验证明角加速度控制驱动防滑的可行性，通过角加速度阈值判定打滑开始和结束，对打滑状态进行线性降转矩。高峰等［17］采用类似方法在客车上进行试验并得到期望的防滑控制效果，但文中设计的防滑介入和退出阈值均是通过大量测试标定获得的常值，且没有考虑车轮弹性变形滑转引起的角加速度，对不同工况的适应性较差。

本文提出的防滑控制算法考虑了车轮滑转，利用角加速度信号给出防滑控制介入和退出的判定准则，并提出相应的切换逻辑和车轮转矩控制方法。同时，给出车轮角加速度信号的获取和矫正方法，并利用实车数据对控制算法进行验证。最后，通过联合仿真分别测试装载机铲土工况和低附着路面加速工况下的防滑控制效果。

1 防滑控制逻辑

1.1 车轮滑转特性分析

进行防滑控制首先需要确定车轮打滑的指标。分布式电驱动装载机4 轮均为驱动轮，通过轮速信号得到的车速信号并不可靠［18］。因此本文避免使用车速信号，而通过分析单个车轮的角加速度变化来判断车轮状态。

1.1.1 打滑开始判定

首先分析整车，假设装载机4 个车轮的滚动半径相等，忽略坡度阻力和空气阻力，考虑装载机工作阻力，则装载机加速行驶时有

式中：a为整车纵向加速度；m为整车质量；Fxi为车轮纵向力；Fw为装载机工作阻力。

车轮在驱动转矩Ti作用下加速转动时受力如图1所示。

图1 轮胎受力分析

此时对车轮进行分析，有

式中：Ti为第i个车轮的驱动转矩；R为滚动半径；Mi为第i个车轮的滚动阻力矩；αi为第i个车轮的角加速度。Mi表示为

式中：e为滚动阻力臂，是路面对车轮反作用力的合力在纵向的偏移量；Fzi为第i个车轮的垂向载荷。

轮胎和路面之间的接触和传力特性比较复杂。车轮驱动整车前进时，车轮的角加速来源于两个部分：一是整车加速换算到车轮的角加速度；二是车轮滑转引入的角加速度。分别考虑两部分的角加速度，首先假设刚性车轮和地面纯滚动，则

式中α为理论车轮的角加速度。

将式（2）分离Fxi，式（4）分离a代入式（1）中整理得到理论车轮角加速度。

式中αdis为受车轮的滚动阻力和工作阻力影响的角加速度。这两个变量随环境变化，一般都难以获得，设4 个车轮平均滚动阻力臂为e，纵向的工作阻力不会超过路面附着条件，即Fw≤mgφ，则可以得到其上界为

式中φ为最大路面附着系数。

若将车轮角加速度式（5）的第一部分作为阈值，则阈值偏大，触发时需要更大驱动转矩，此时转矩超量引起的该部分附加角加速度为

式中Tadd为超量的转矩。

以转矩超量为代价，触发阈值的条件是附加角加速度大于受环境影响引起的角加速度：

则能触发的超量转矩为

假设4 个车轮完全相同，单个车轮临界打滑的车轮转矩为

则可以保证触发的转矩超量率为

因为mR2＞＞4J，超量的转矩相对很小，所以将车轮角加速度式（5）的第一部分作为阈值αref。因为αref＞α，所以不会使防滑算法因始终在临界值附近而经常触发，算法可靠性更高，能充分发挥路面的附着系数。

再考虑滑转对角加速度的影响。车轮滑转原因包括轮胎滑转和土壤剪切变形两部分。两种原因下的滑转特性曲线变化趋势近似［19-20］均如图2 所示。当滑转率曲线处于OA段时，附着系数和滑转率正相关。在这种情形下，车轮和地面之间的滑转由轮胎弹性变形和车轮正常截切土壤形成推土积压效应引起，是车轮驱动力产生的基础，不认为出现了打滑。而AB段和OA段曲线斜率存在明显不同。A点附近一般认为是出现打滑的分界位置。

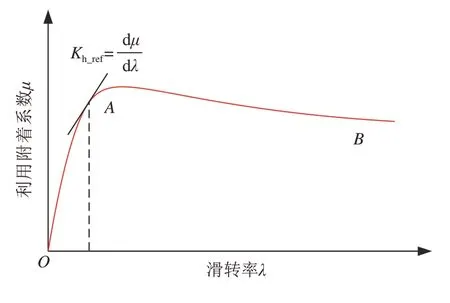
图2 轮胎μ-s曲线

如图2所示，对于μ-s曲线，其斜率为

由式（2）将附着系数改写为

假设垂向载荷不发生变化，滚动阻力矩为常值，车轮仅在线性区滑转，角加速度保持相对稳定，可以忽略其微分值。则对式（14）两边微分后得

根据滑转率的定义，有

因为滑转时车速变化相对缓慢可视为常数，对式（16）两边进行微分。又因为在线性区滑转率较小，进一步近似得到v≈ωiR，则

因此，通过式（13）、式（15）和式（17），计算车轮滑转引起的角加速度：

由图2 可知，当斜率Kh＞Kh_ref时为OA段，车轮不打滑，反之则判定为打滑。将式（18）中的Kh代入Kh_ref得到车轮滑转引起的角加速阈值Δαi_ref。当Kh＞Kh_ref时Δαi＜Δαi_ref，阈值大于滑转引起的角加速度，不会触发；反之Δαi＞Δαi_ref，则角加速度超过阈值，触发防滑控制。

综上两方面原因，再考虑角加速度信号获取的误差以及模型的近似，引入容差角加速度α0，则车辆在滑转率线性区域加速时不出现打滑的车轮角加速度阈值为

1.1.2 打滑结束的判定

当车轮出现打滑后，通过降低电机转矩输出减小打滑现象，防止车轮失速飞转。分析此时车轮的受力，车轮的纵向力由垂向载荷和滑动摩擦因数决定，根据式（2）车轮的角加速度为

假设打滑瞬时过程中车轮垂向载荷不发生明显变化，忽略滚动阻力臂变化。则引起角加速度变化的主要因素是驱动力减小和附着系数μ的变化。

在降转矩阶段驱动转矩持续降低，轮速下降，滑转率减小。对于利用附着系数，如图2 所示，当滑转率在BA段时，滑转率变小时附着系数μ变大。根据式（20），降低的转矩和变大的附着系数使角加速度持续减小。而当轮速进一步降低进入AO段时，附着系数开始急剧减小。若此时为负的角加速度开始变大，则说明车轮滑转结束。即车轮打滑结束的标志为角加速度α＜0且出现极值=0。

1.2 切换逻辑和控制方法

根据车轮是否打滑，可以将车轮分成两个状态分别进行降低转矩控制和转矩过渡控制。控制逻辑框图如图3所示。

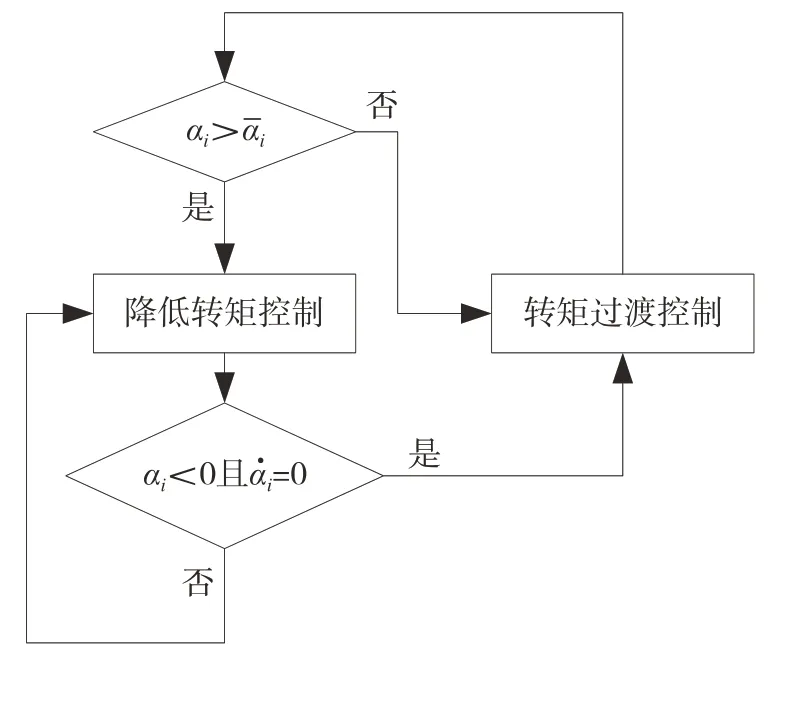
图3 控制逻辑框图

当判定车轮出现打滑后，对车轮进行降转矩控制。此时在减小转矩的同时，需要和驾驶员变化的需求转矩融合。为快速持续减小转矩，防止长时间打滑，设计指数形式的转矩下降规律，转矩的递推关系式为

式中：Ti(k)为打滑时刻的车轮驱动转矩；t0为控制器步长；t1为降转矩响应时间为下一时刻的预输出转矩。

将预输出的转矩和本时刻驾驶员的需求转矩进行融合得到下一时刻的输出转矩，融合方式为两者取小：

当判定为车轮打滑结束后，对车轮进行转矩过渡控制。当打滑结束时实际车轮的转矩较小而驾驶员需求的转矩可能较大，转矩突变会引起冲击。因此对于需求转矩较大的情况，按照一定的过渡时间对车轮的实际输出转矩进行过渡控制，输出转矩的递推关系式为

式中t2为过渡响应时间。

2 轮速信号处理

本文采用的防滑控制方法需要车轮的角加速度和角加速度的微分信号。而实车上可以获得的仅为车轮转速信号。因为轮速信号本身就存在一定干扰［21］，直接微分会将干扰信号放大影响控制的品质。为得到高品质的微分信号，韩京清［22］基于等时区方法设计了离散最速跟踪器，并应用于自抗扰控制。孙彪等［23］改进了离散最速微分跟踪器使之不会出现超调且到达稳态的时间更短。经过多年来的研究改进该方法进一步得到完善［24］。

2.1 离散最速微分跟踪器

最速微分跟踪器将微分问题转化为2阶串联积分系统在输入受限的条件下以跟踪时间作为性能指标的最优控制问题。输入受限的2阶串联积分系统为

连续系统采用开关控制（Bang-Bang 控制）可以得到开关曲线方程，理论上在合适的时间点上仅需要经过一次切换就可以到达控制目标。然而对于离散控制系统受限于固定步长，直接离散开关曲线方程会出现振荡。因此采用最速控制综合函数来近似开关曲线方程。离散2阶串联积分系统为

其中一种离散最速控制综合函数u(k)=fsun(x1(k)，x2(k)，r，h)的具体形式为

式中：r为输入的限制，r越大跟踪速度越快，因此也称为速度因子；h为离散微分跟踪器步长，步长越大受局部扰动影响越小，滤波效果越好，因此也称为滤波因子，但步长越长也会导致延迟越严重；sign(·)为符号函数；fix(·)为向0取整函数；sat(·)为饱和函数，形式为

式（26）得到的最速控制综合函数是将任意状态的系统变化到原点。需要跟踪轮速信号仅修改最速综合函数为u(k)=fsun(x1(k)-ω(k)，x2(k)，r，h)，得到的角加速度为α-(k)=x2(k)。

2.2 角加速度预估矫正

因对输入的幅值进行了限制，所以用最速微分跟踪器得到的微分信号具有一定的滤波效果，保证了信号质量，但是跟踪不可避免会出现延迟。而角加速度作为门限值，需要及时启动防滑控制，要求延时越小越好。利用角加速度的微分信号对角加速度进行预估可以减小相位的延时，角加速度预估校正后为

式中：α-(k)为微分跟踪器输出的角加速度；Kc为相位校正系数；为角加速度微分信号。

将包含随机干扰的正弦信号作为轮速信号，图4 是通过直接微分(x(k)-x(k-1))/h、最速微分跟踪器以及经过预估校正后的角加速度信号。对于含有噪声的轮速信号，直接微分得到的角加速度几乎是不可用的；用微分跟踪器得到的信号整体上比较平滑但存在延时；而预估矫正后的微分信号逼近了理想微分信号，可以较为快速准确地判断出现打滑的时刻。

图4 不同方式获得的角加速度信号

如图5 所示，因为滤波之后的角加速度信号仍有小幅的波动，难以通过角加速度信号准确地获得极点的位置，但再次通过微分跟踪器得到的角加速度的微分信号可以较为准确的得到零点位置。蓝色虚线为理想微分的极值位置。因为角加速度微分信号也存在波动，稍有延后的零点位置的判断使防滑算法的退出更加可靠。

图5 角加速度极值和角加速度微分零点比较

3 实车数据验证

装载机作业循环工况一般称为“V 型工况”，即装载机放下铲斗、前进、插入料堆、铲起料堆、后退、卸料的过程。四轮分布式电驱动装载机进行铲土作业时情形如图6所示。

图6 四轮独立分布式电驱动装载机

装载机的轮边电机可以反馈转速和转矩信号，利用轮边减速比可以换算得到车轮转速和转矩值，如图7所示。图例FL、FR、RL、RR 分别表示左前轮、右前轮、左后轮、右后轮。轮速为正值表示前进，负值表示后退。图中转矩为正值表示驱动，负值表示再生制动，转矩驱动前进后退的方向是通过标志位控制的。因为行驶方向与防滑无关，在计算触发门限值时，统一取绝对值之后进行处理。

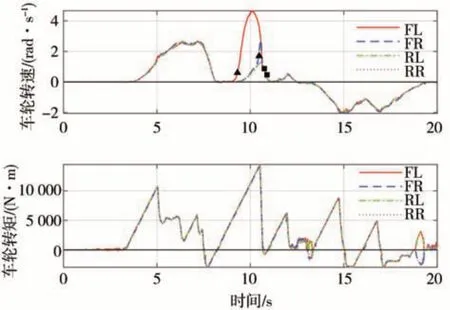
图7 某个“V型工况”车轮的转速和转矩

图7 所示的轮速信号中左前轮和右前轮在9和10.4 s 左右先后出现了滑转。在8～9.5 s 的过程中，装载机由于铲斗插入料堆轮速几乎为零，而此时需要充分发挥路面附着系数以便铲起更多的物料。

因装载机车速信号难以获取，分析图7 可知后轮没有出现打滑，若以后轮的平均轮速换算成车速计算滑转率，则车辆的滑转率如图8 所示。在8～9.5 s 4 轮的滑转率均剧烈变化，因此铲土作业时以滑转率作为控制量进行防滑控制几乎不可行。

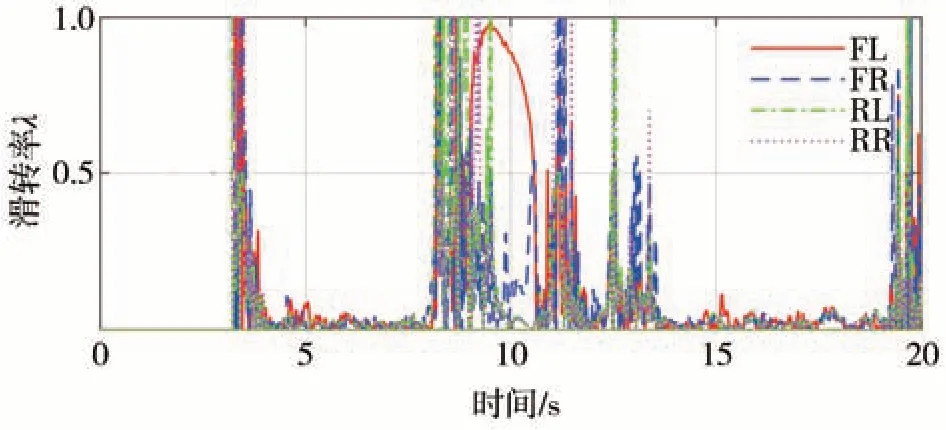
图8 4个车轮的滑转率

将轮速和转矩数据代入上述角加速度门限的防滑控制模型中。图9 所示为角加速度及其触发阈值，角加速度超过阈值时为车轮出现打滑的时刻，在图7中用▲进行了标注。

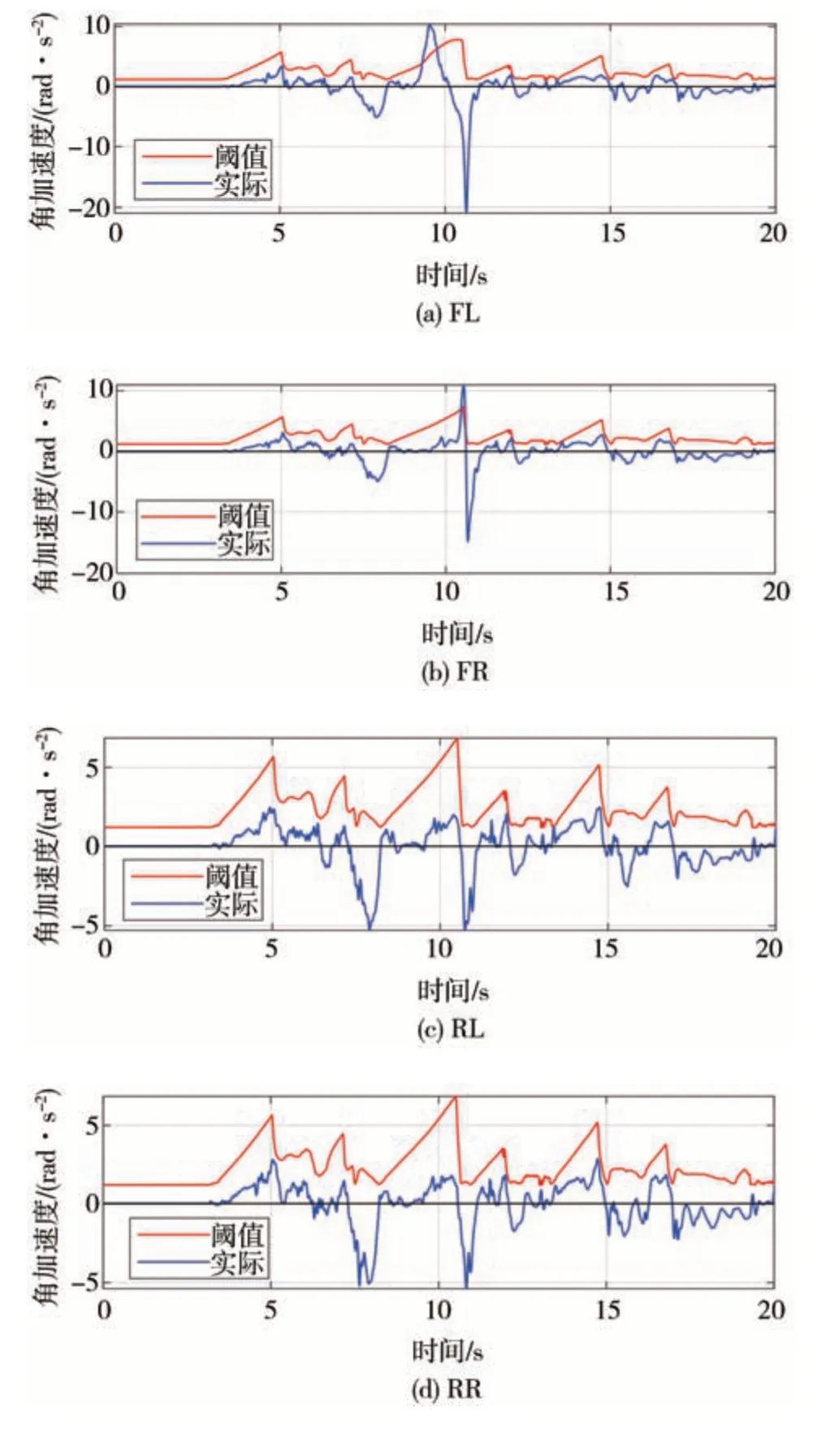
图9 车轮角加速度及其触发阈值

图10 角加速度微分

4 仿真

由于物料堆的不确定性，进行实验对比很困难，因此采用ADAMS 和Simulink 的联合仿真来对比验证防滑控制算法性能。本文采用的是ADAMS的UA轮胎模型，该轮胎模型能较为准确地刻画低速时的轮胎纵向特性。装载机整车和轮胎的相关参数如表1所示。

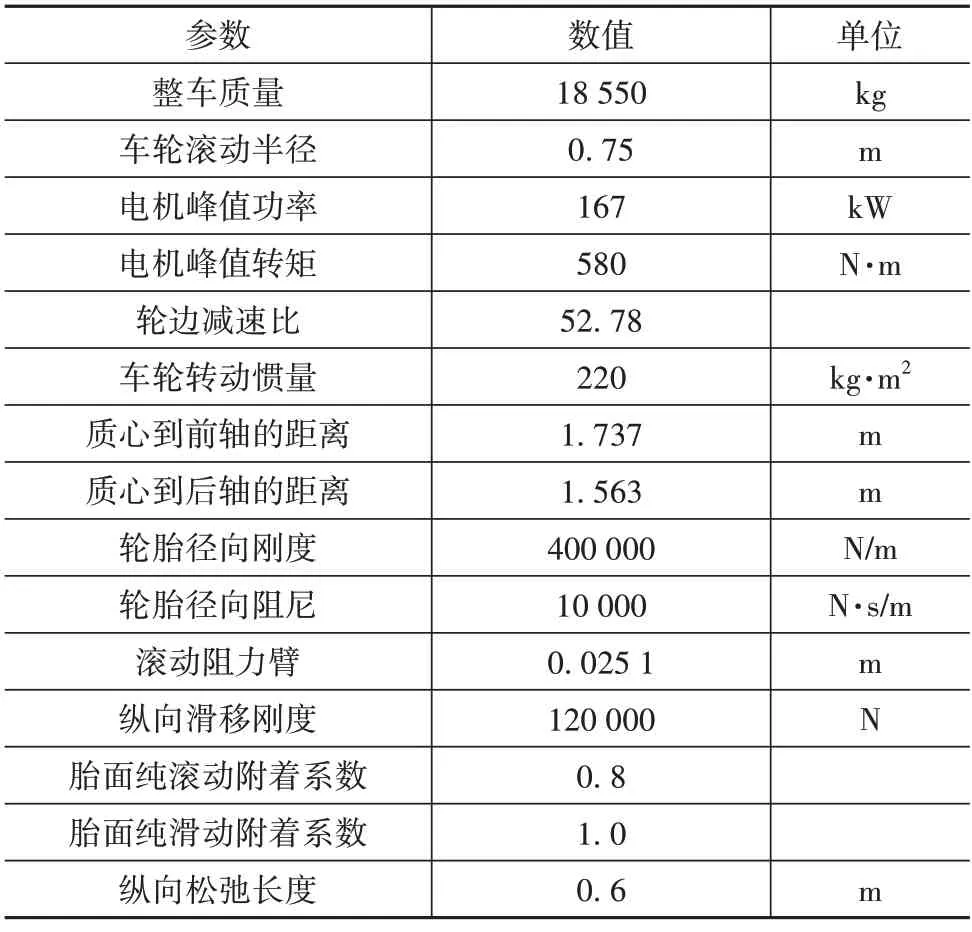
表1 装载机和轮胎基本参数表

滑转率的防滑控制在接近零车速时无法计算，可以采用滑转量来衡量。但滑转量的计算仍需要车速信号，因此以最小轮速衡量其他车轮的相对滑转情况。以相对滑转量作为反馈信号得到的防滑控制转矩为

仿真时将该控制策略和本方法进行对比。

4.1 铲土工况

设置路面附着系数0.5，用弹簧阻尼来模拟装载机在铲掘料堆时的工况。将推铲力方向设置为倾斜，以模拟其影响车轮轴荷时的防滑控制效果。料堆和装载机的关系如图11所示。

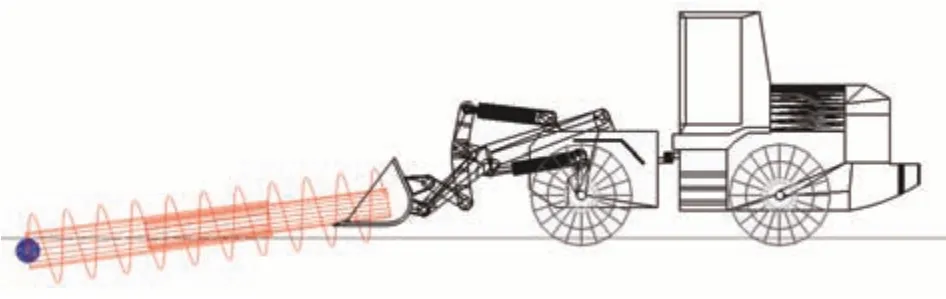
图11 装载机模和模拟料堆关系图

装载机4 个车轮的需求转矩一般平均分配。如图12 所示，轮端的需求转矩从零开始先增加到12 kN·m，再增加到21 kN·m，最后回到12 kN·m，以测试防滑算法的介入、退出机制和应对部分车轮打滑与全部车轮打滑时的控制效果。对角加速度门限控制方式，前轮在接近12 kN·m 时开始介入防滑控制，输出转矩开始振荡直到整个过程结束；后轮则在接近21 kN·m 时介入防滑控制，并在需求转矩降低之后退出。采用相对滑转量控制方式，后轮曲线和无控制时完全重合，算法对轮速最小的车轮不起作用，前轮曲线基本和无防滑控制时一致，但在全部车轮出现打滑和退出时出现两个转矩波动。

图12 铲土工况驾驶员需求转矩和实际转矩

将车轮转速和滚动半径的乘积ωiR等效值和车速放在一张图上，如图13 所示，角加速度门限控制和无防滑控制的车速几乎相同。无防滑控制前轮在12 kN·m 需求转矩下就失速滑转，最后稳定在电机外特性限制的轮速下；后轮在12 kN·m 需求转矩下不打滑，而当转矩增大到21 kN·m 时也失速滑转。角加速度门限控制的轮速在转矩过大时仅出现了小的峰值，即滑转一下之后马上停下，每次滑转的角度在30°以下。滑转时推土积压有利于充分发挥路面附着系数，又可以防止车轮连续滑转甩起土块石子。

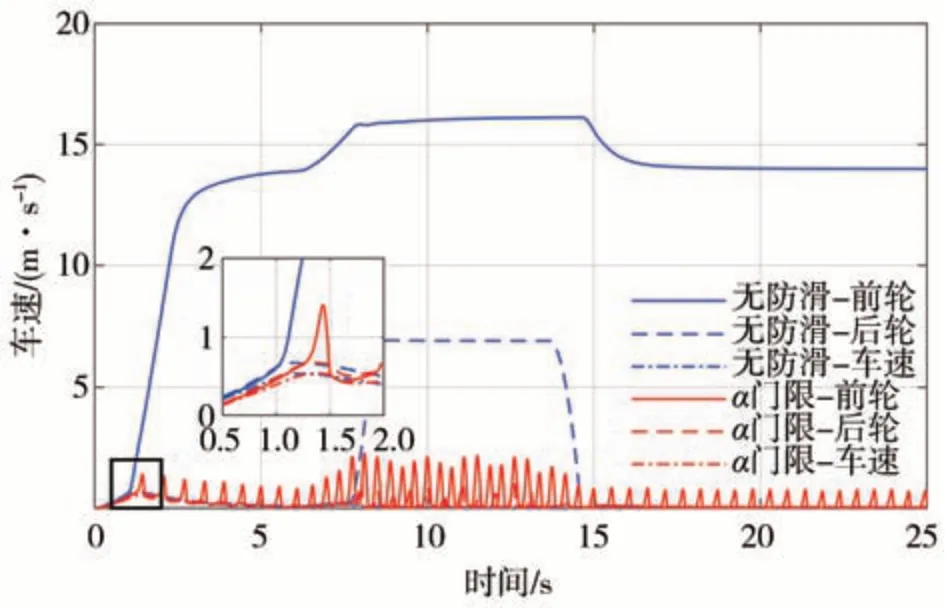
图13 铲土工况轮速等效的车速和车速

图14 中对比了两种控制策略下车速的变化。采用相对滑转量控制方式在仅部分车轮打滑时对其他车轮实现防滑，且轮速波动较小，但该控制方式在所有车轮都打滑时就会失效，此时更容易造成危险。

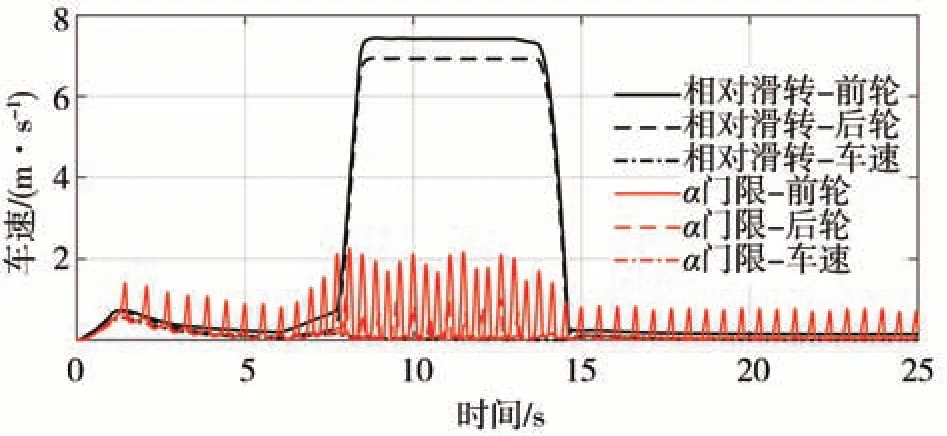
图14 铲土工况两种控制方式车速情况对比

图15 所示为作用在料堆上的推铲力变化曲线。角加速度门限控制的推铲力略小于无防滑控制和相对滑转量控制的推铲力，且小幅波动。实际上，当车轮剧烈滑转时会搅动路面土层，不利于发挥路面附着，反而会使推铲力下降。

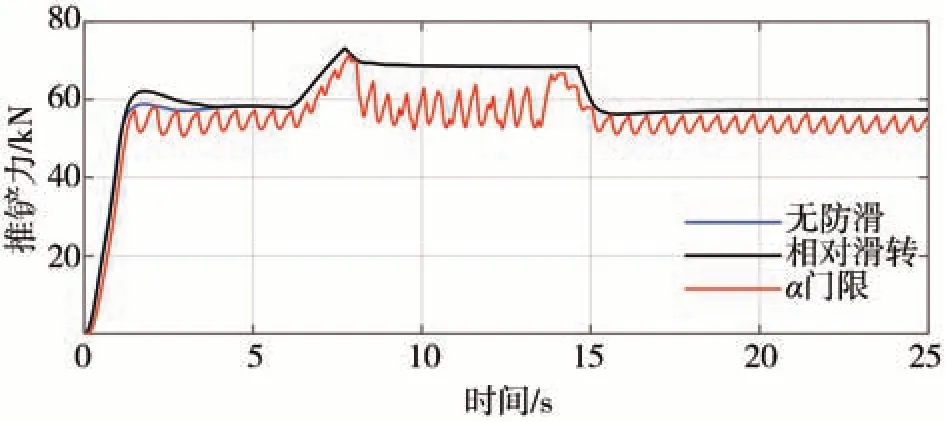
图15 铲土工况推铲力变化曲线

图16 所示为铲土过程中的前后载荷。受料堆反作用力的影响，前轴载荷减小，后轴载荷增加。该防滑算法在车轮载荷明显发生变化的条件下依然能保持较好的防滑控制效果。

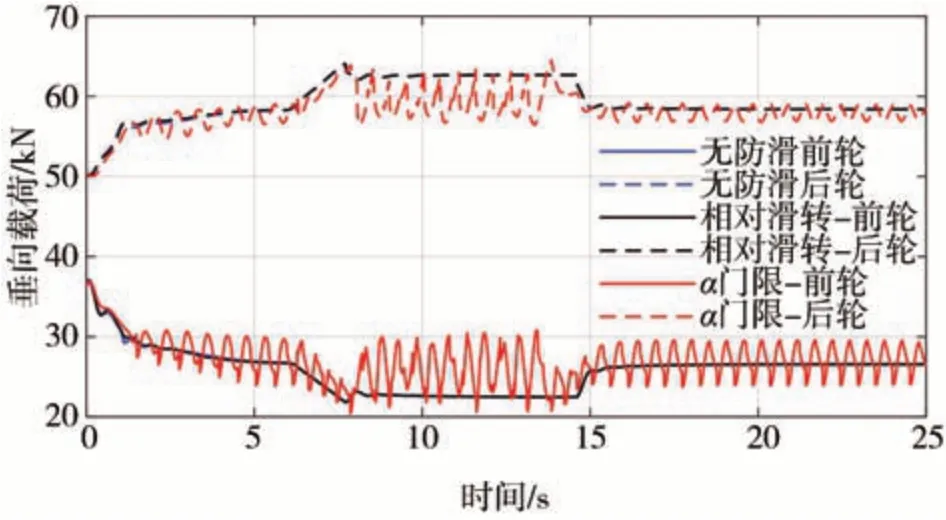
图16 铲土工况装载机前后轮垂向载荷

4.2 低附路面加速工况

设置路面附着系数0.2，不设置工作负载，施加12 kN·m的驱动转矩令装载机直线加速。

如图17 所示，对于无防滑控制的装载机，轮速迅速升高到电机外特性限制的最大值，即使采用相对滑转量控制方式的前后车轮也同时打滑，而采用角加速度门限控制的装载机，轮速振荡但没有失控。随着车速的提高驱动转矩变小，当驱动转矩小于路面附着极限后不再出现打滑。

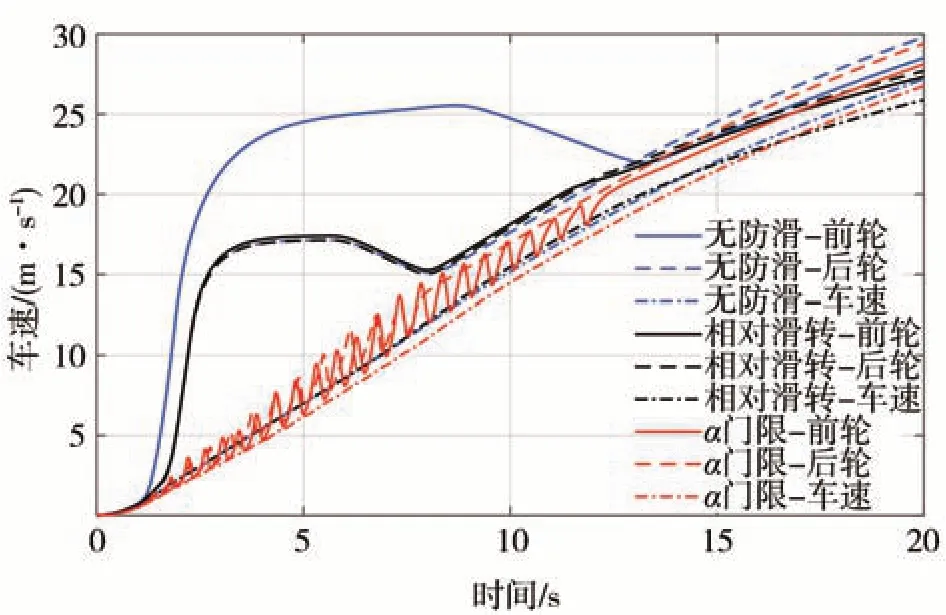
图17 低附加速工况轮速等效的车速和车速

通过车速和轮速可以计算滑转率，如图18 所示，当车速较低时滑转率均剧烈波动，在车速升高后，无防滑控制和相对滑转量控制的车辆前后轮滑转率均变为较大值。对于角加速度逻辑门限控制方式，滑转率在最佳滑转率附近波动，最大也不超过0.4。

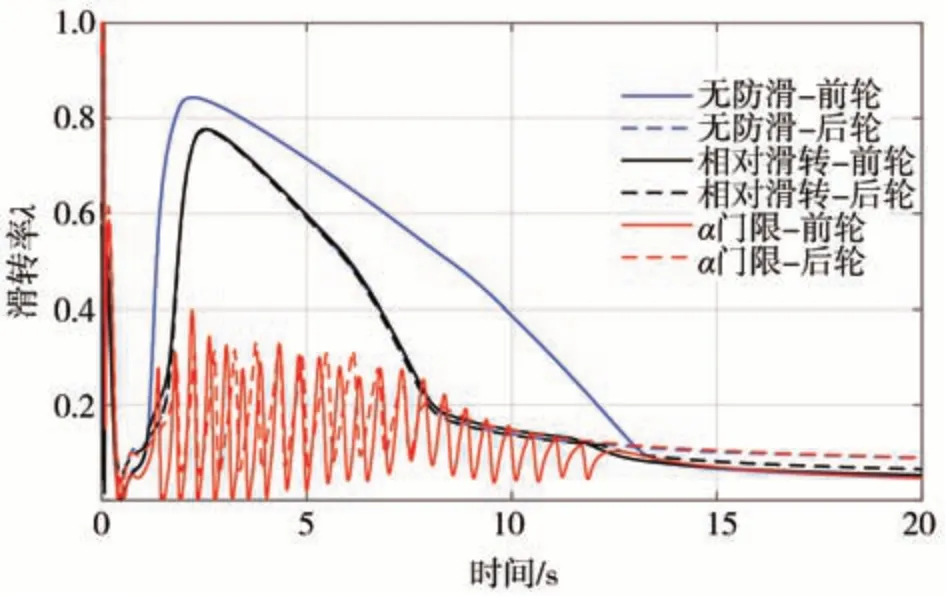
图18 低附加速工况滑转率变化曲线

图19为转矩的变化曲线。输出转矩可以分成3个阶段：第1 阶段需求转矩较小不超过路面附着条件，不出现打滑现象，转矩按照需求变化；第2 阶段，需求的转矩和电机外特性限制的转矩都超过路面附着条件，角加速度逻辑门限控制方式下，驱动转矩反复振荡使车轮不出现持续打滑，而无防滑控制时电机转矩输出接近保持恒转矩；第3 阶段，轮速较高，在外特性限制下转矩小于路面附着条件，输出转矩按照电机外特性曲线变化。因为相同滑转率在高速阶段滑转量较大，所以相对滑转量控制虽然在低速时可以避免滑转率计算时分母为零的问题，但在高速行驶的第3阶段会使转矩输出受到限制，通用性较差。

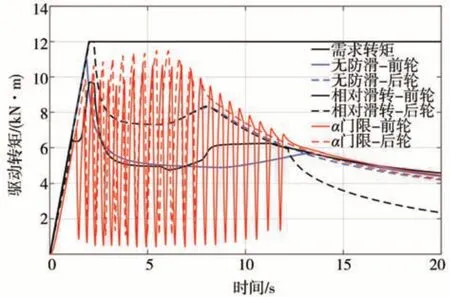
图19 低附加速工况驾驶员需求转矩和实际转矩

5 结论

对于装载机长时间接近零车速的铲土工况和复杂变化的路面条件，传统基于滑转率的防滑控制算法难以应对。本文提出的基于车轮角加速度逻辑门限的分布式电驱动装载机驱动防滑算法具有以下特点：

（1）控制架构比较简单，计算量小。不需要车速信号，只利用车轮转速和转矩信号，可以实现4 轮同时打滑、车速接近于零的恶劣工况长时间进行防滑控制，并比较充分地发挥路面附着系数。

（2）参数物理含义清晰，算法的适用性广。对不同作业工况、不同路面附着系数、不同载荷变化下均有较好的防滑控制效果。

（3）防滑控制介入时输出转矩具有波动性。车轮转矩波动对驾驶员的舒适性有一定的影响，但对于装载机来说在一定程度上利于驾驶员感知到车轮打滑的情况，使其及时做出调整。