相对于Gorenstein内射预包络复形的同调维数

吴德军, 赵晓宇

(兰州理工大学 理学院, 甘肃 兰州 730050)

1996年,Enochs等[1]介绍了复形范畴的正交理论.1998年,佟文廷[2]介绍了环模复形的同调理论.1999年,Rozas[3]介绍并研究了模的复形范畴的覆盖与包络,并给出了特殊的覆盖与包络的定义.2002年,Avramov等[4]研究了具有有限Gorenstein维数的绝对、相对和Tate上同调模.2004年,Holm[5]深入研究了Gorenstein同调维数,许多代数工作者在这篇文献的基础上研究了很多相关模类.2011年,Yang等[6]给出了任意结合环上的Gorenstein投射复形、 内射复形和平坦复形的相关结论.2011年,Yang[7]研究了一般环上的Gorenstein投射复形、 内射复形和平坦复形的性质,例如: 设C是复形.则C是Gorenstein内射复形当且仅当Cm是Gorenstein内射模.2015年,章璞[8]讨论了复形的同伦交换图和相关性质.2017年,Christensen等[9]深入研究了无界复形的Gorenstein维数,并证明了新的与复形的Gorenstein维数等价的结论.2018年,Liu[10]介绍和研究了复形的严格的Gorenstein投射预覆盖,即:设C是复形,f:G→C是满的Gorenstein投射预覆盖.若ker(f)是具有有限投射维数的复形,则称f是C的严格的Gorenstein投射预覆盖.2021年,Liu等[11]介绍和研究了相对于Gorenstein投射预覆盖复形的同调维数,Gppd(X),并证明了新的同调不变量的相关性质.受以上文献的启发,本文讨论了相对于Gorenstein内射预包络复形的同调维数和相关性质.

定义1设X是复形.相对于Gorenstein内射预包络复形的同调维数,Gipd(X),定义为

若复形I不存在,则Gipd(X)=∞.

定义2设E和I是Gorenstein内射复形,f:E→I是单的复形同态.若复形coker(f)是正合上有界的,则称f是几乎余同构.

注1coker(f)是Gorenstein内射复形.

定理1设I是Gorenstein内射复形.则

Gipd(I)=inf{n∈Z|inf H(I)≥

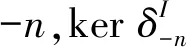
inf{-infE|E→I是几乎余同构}

1) Gipd(I)=s.

(1) Gipd(I)≤s.

设φ:I→I是复形同构.则存在复形的短正合列

其中,cokerφ=0.因为对任意的Gorenstein内射复形I′,Hom(I,I′)→Hom(I,I′)是满的,Ext1(cokerφ,I′)=0,所以φ:I→I是I的特殊的Gorenstein内射预包络.

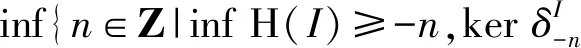
证得Gipd(I)≤s.

(2) Gipd(I)≥s.

设Gipd(I)=n∈Z.根据相对于Gorenstein内射预包络复形的同调维数的定义,存在I的特殊的Gorenstein内射预包络φ:I→E,Ext1(cokerφ,E′)=0,E′是任意的Gorenstein内射复形.因为φ:I→E是可裂的,所以对复形的短正合列

E≃I⊕cokerφ.因为infH(E)≥-n,所以

inf H(I)≥-n

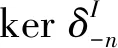
由复形的短正合列交换图,构造交换图1,使得图1在-n处正合.

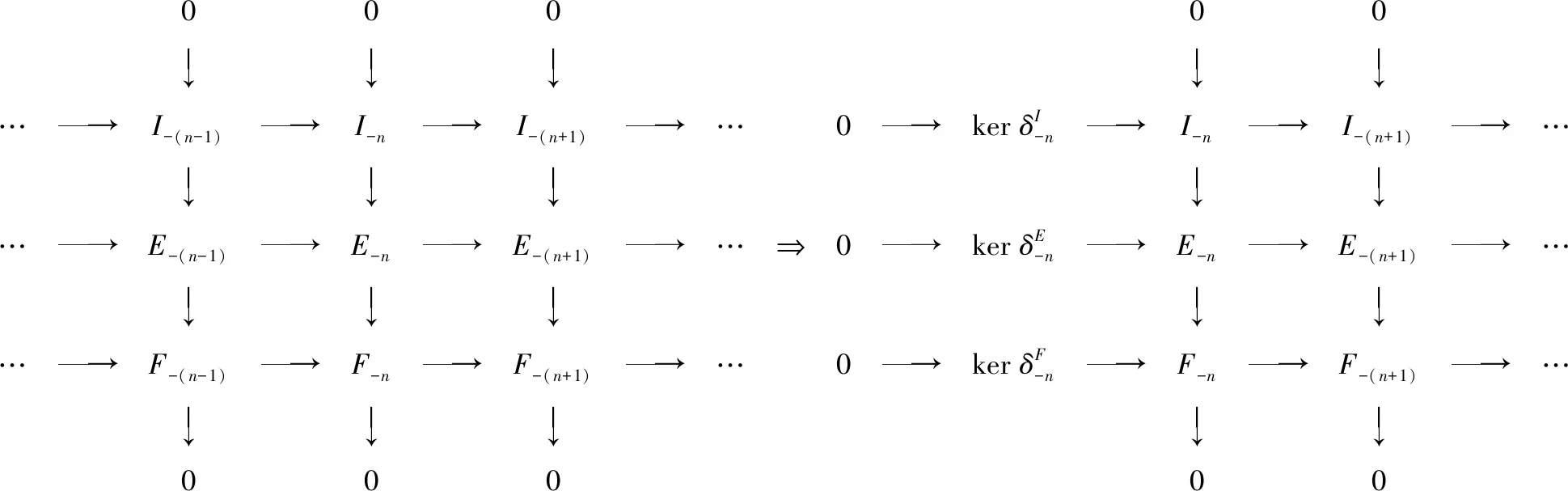
图1 交换图

构造行正合交换图2.

图2 交换图

2)s=t.

(1)s≥t.

若s=∞, 不等式显然成立;

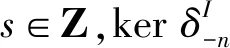
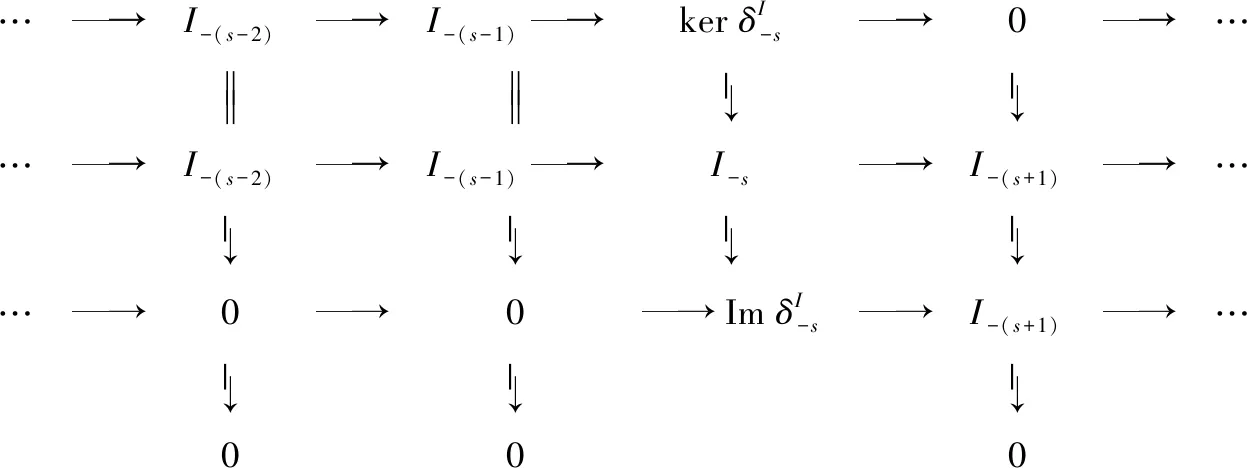
图3 交换图

由图3可得正合序列

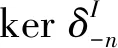
(2)s≤t.

若t=∞, 不等式显然成立;

设supF=sup{i∈Z|Fi≠0}=-m.记

将上面的长正合序列打断可得

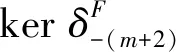
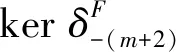
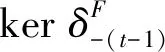
根据蛇引理,考虑交换图4.

图4 交换图

根据图4和蛇引理可得正合序列

下证复形I在-(t+1)处正合.

由图4可知,g是满同态.

因为复形I在-(t+1)处正合, 所以inf H(I)≥-t.证得s≤t.

由定理1, 可得如下命题.

命题1设X是复形.则

Gipd(X)=inf{-infE|存在复形同态X→I←E,X→I是X的特殊的Gorenstein内射预包络,E→I是几乎余同构}

根据文献[9]中命题3.6,可以给出如下复形X的Gorenstein内射维数的定义.

定义3设X是复形.则复形X的Gorenstein内射维数,Gid(X),定义为

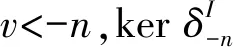
命题2设X是复形.则

证明设φ:X→I是X的DG-内射分解.因为正合复形和DG-内射复形正交, Ext1(cokerφ,I)=0,所以φ:X→I是X的特殊的DG-内射预包络.

设φ:X→I是X的特殊的DG-内射预包络.则Ext1(cokerφ,I)=0, cokerφ是正合复形.存在复形的短正合列

因此φ:X→I是X的DG-内射分解.

定义4设X是复形,φ:X→I是X的单的Gorenstein内射预包络.若cokerφ是具有有限内射维数的复形, 则称φ:X→I是X的严格的Gorenstein内射预包络.

命题3设X和X′是左R-模复形,φ:X→I和φ′:X′→I′分别是X和X′的严格的Gorenstein内射预包络.则对任意的α:X→X′, 存在β:I→I′使得图5可交换.

图5 交换图

证明对任意的α:X→X′,φ′α∈Hom(X,I′).因为φ:X→I是X的严格的Gorenstein内射预包络, 所以存在β:I→I′, 使得φ′α=βφ, 图5可交换.

引理1[4]设B,C和I是复形,β:B→C是复形同态,HomR(β,I):HomR(C,I)→HomR(B,I)是拟同构.则对每一个同态α:B→I,存在同态γ:C→I,使得γβ～α.若HomR(β,I)是满的,则γβ=α.若α′:B→I,γ′:C→I满足α′～α,γ′β～α′,则γ′～γ.

引理2[8]设有复形的同伦交换图6.

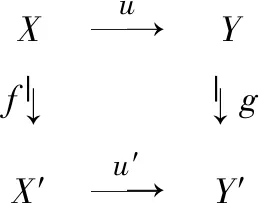
图6 交换图

图7 交换图

命题4设X和X′是左R-模复形,ψ:X→E和ψ′:X′→E′分别是X和X′的单的DG-内射分解,φ:X→I和φ′:X′→I′分别是X和X′的严格的Gorenstein内射预包络.则存在λ:I→E和λ′:I′→E′, 使得ψ=λφ,ψ′=λ′φ′.设α:X→X′是复形同态.根据命题3, 存在β:I→I′, 使得φ′α=βφ.根据引理1,存在γ:E→E′,使得γψ～ψ′α.

1) 证明: 存在行正合的复形交换图8.

图8 交换图

2) 存在交换图9.证明:λ′β～γλ.

图9 交换图

证明1) 设σ:I→Q是I的单的DG-内射分解. 则存在复形的正合列:

其中,H是正合复形.因为E′是DG-内射复形,所 以Ext1(H,E′)=0,Hom(Q,E′)→Hom(I,E′)是满的,即对于λ′β:I→E′, 存在μ:Q→E′, 使得λ′β=μσ.类似地, 对于γλ:I→E′, 存在ν:Q→E′, 使得γλ=νσ.

(1)

由式(1)可得,μ～ν.根据引理1, 证得λ′β～γλ.

2) 由1)得,λ′β～γλ.根据引理2, 存在

使得图10交换.

图10 交换图

因此, 存在行正合的复形交换图8.

引理3[6]设C是具有有限Gorenstein内射维数n的复形.则C具有单的Gorenstein内射预包络φ:C→G, 使得cokerφ的内射维数是n-1.若n=0, 记cokerφ=0.

引理4[6]设G是Gorenstein内射复形,T是具有有限投射维数或内射维数的复形.则Exti(T,G)=0,其中i≥1.

定理2设X=…→0→X-1→X-2→…→X-(s-1)→X-s→0→…是有界复形.则

Gipd(X)≤max{Gid(X-i)+i|i=0,1 ,…,s}

(2)

证明设max{Gid(X-i)+i|i=0,1 , …,s}=n.

1) 当n=∞时, 不等式显然成立;

-inf(I)≤max{Gid(X-i)+i|i=0,1 ,…,s}

下面通过数学归纳法证明不等式成立.

其中,E-i是内射模,i=1,2,…,n.记

则存在的复形的短正合列

-inf(I)≤max{Gid(X-i)+i|i=0,1 ,…,s-1}

考虑复形态射交换图11.

图11 交换图

由图11可知,Y和Z是有界复形.根据映射锥的定义,X=Cone(δ).由假设可知,分别存在Y和Z

-inf(IY)≤max{Gid(X-i)+i|i=0,1 ,…,s-1},-inf(IZ)≤Gid(X-s)+s-1

根据命题3,存在交换图12.

图12 交换图

根据命题4,存在交换图13.

图13 交换图

由图13可知,φ[-1]是单的.因为IZ[-1]和IY是Gorenstein内射复形,所以Cone (α)[-1]是Gorenstein内射复形.根据蛇引理,存在下面的复形正合列:

用Hom (-,H)作用在上面的复形短正合列上,根据引理4,因为

所以

Ext1(coker(φ[-1]),H)=0

(3)

证得不等式成立.