三角矩阵环上投射余可解的Gorenstein AC-平坦模

秦军霞, 张翠萍

(西北师范大学 数学与统计学院, 甘肃 兰州 730070)

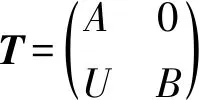
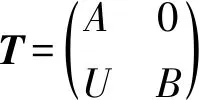
1 预备知识

本文所涉及的环均指有单位元的结合环,模均指酉模.下面给出本文用到的一些概念和事实.

定义1[3]称左R-模M是FP∞型的,如果存在左R-模的正合列

…→Pn→…→P1→P0→M→0

其中Pi(i≥0)是有限生成投射模.

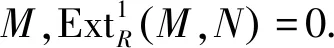
设G是右R-模,G的absolutely clean维数定义为AC-dR(G)=inf{n∈Z|存在右R-模的正合列

0→G→L0→…→Ln-1→Ln→0

其中Li(0≤i≤n)是absolutely clean模},若这样的n不存在,则记AC-dR(G)=∞.记

rAC-d(R)=sup{AC-dR(G)|G是右R-模}

定义3[4]称左R-模M是Gorenstein AC-平坦模,如果存在平坦左R-模的正合列

F∶…→F1→F0→F-1→…

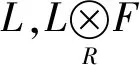
设A,B是环,U是(B,A)-双模.设

其乘法定义为

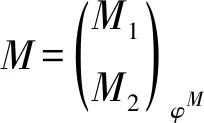
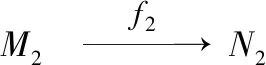
图1 交换图

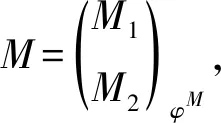
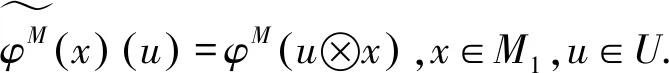
图2 交换图

左T-模序列

正合当且仅当0→M′1→M1→M″1→0和0→M′2→M2→M″2→0正合.关于该环的细节参见文献[2].

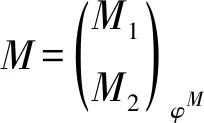
其中子群

H={ψN(x2⊗u)⊗y1-x2⊗

φM(u⊗y1)|x2∈N2,y1∈M1,u∈U}

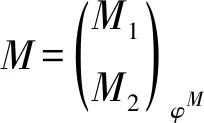
引理2[8]设UA是有限生成投射模,BU是平坦模,L=(L1,L2)φL是右T-模.

1) 如果L是absolutely clean右T-模,那么L1是absolutely clean右A-模且L2是absolutely clean右B-模.

引理3设UA是有限生成投射模,BU是平坦模,M2是右B-模.如果AC-dB(M2)<∞,那么AC-dT(0,M2)<∞.

2 主要结果

定义4称左R-模M是投射余可解的Gorenstein AC-平坦模,如果存在投射左R-模的正合列

P∶…→P-1→P0→P1→…

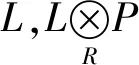
显然PGACF-模是Gorenstein AC-平坦模.以下讨论环T上的PGACF-模与环A上的PGACF-模和环B上的PGACF-模之间的关系.

引理4设M是左R-模,则下列条件等价:

1)M是PGACF-模;

2) 存在左R-模的正合列

P∶…P-1→P0→P1→…

证明2)⟹1) 显然.

1)⟹2) 因为M是PGACF-模,所以存在投射左R-模的正合列

P∶…→P-1→P0→P1→…

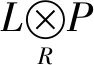
0→G→G0→…→Gn-1→Gn→0

其中Gi(0≤i≤n)是absolutely clean模.由于Pi(i∈Z)是投射左R-模,所以

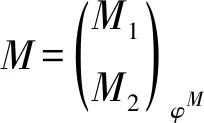
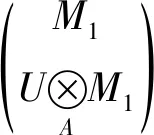
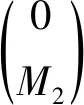
证明1) 因为M1是PGACF左A-模,所以存在投射左A-模的正合列

0→(L1,0)→(L1,L2)→(0,L2)→0

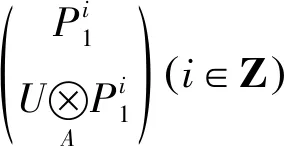
由文献[9]中的命题3.6.1知:

因此对任意整数i,有

所以

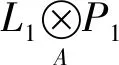
2) 因为M2是PGACF左B-模,所以存在投射左B-模的正合列

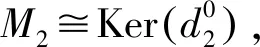
使得

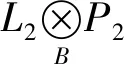
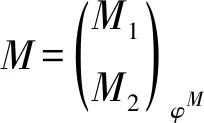
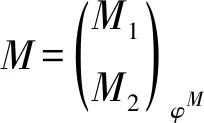
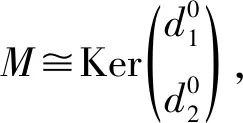
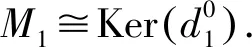
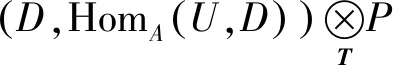
AC-dB(HomA(U,D))<∞

从而由引理3知:

AC-dT((0,HomA(U,D)))<∞

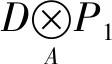
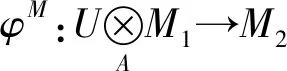
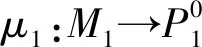
图3 交换图

最后证Coker(φM)=M2/Im(φM)是PGACF左B-模.

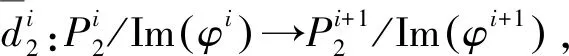
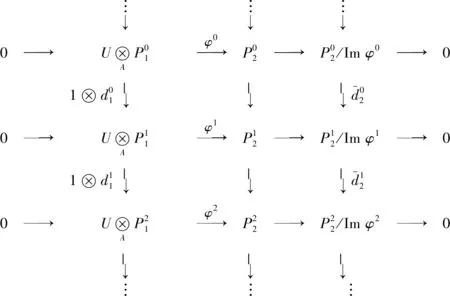
图4 交换图

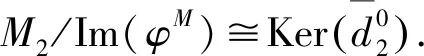
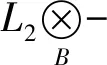
因此有

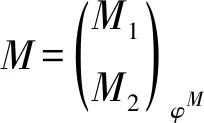
由定理1得以下推论.

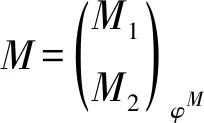
证明因为φM是单同态,所以存在左T-模的正合列