保守系统的类混沌吸引子共存分析及图像加密

颜闽秀, 张 萍

(1. 沈阳化工大学 信息工程学院, 辽宁 沈阳 110142; 2. 工业环境-资源协同控制与优化技术辽宁省高校重点实验室, 辽宁 沈阳 110142)

20世纪60年代初,洛伦兹发表一篇关于大气湍流的论文[1],引发了各位学者们对混沌[2]现象的思考和探究.随后,学者们对混沌的研究与应用取得了很好的成果[3-5].混沌系统一般主要分为耗散混沌系统[6]和保守混沌系统[7].理论上,耗散混沌系统相空间体积是坍塌的,且存在混沌吸引子;而保守混沌系统是不存在混沌吸引子的,而是类似于混沌吸引子[8].除此,保守混沌系统的李雅普诺夫指数和为0,而且保守混沌系统的哈密顿能量函数是一个常数,若满足时间导数为0,说明系统在能量上也是保守的[9].

与耗散混沌系统相比,保守混沌系统的数量稀少,且一般存在隐藏类混沌吸引子.具有隐藏类吸引子的混沌系统安全性远远优于普通混沌系统[10].因此学者们对于保守混沌系统的动力学探究也越来越关注.例如,董恩增等[11]提出了一类哈密顿保守混沌系统,分析该系统的多稳态性以及随机性,并通过FPGA进行硬件实现.王泽等[12]提出了将三端忆阻器嵌入到四维系统中构造出一个新的保守混沌系统,同时分析了混沌系统的动力学特性.Jafari等[13]定义了不同的保守流并进行了分类.齐国元等[14]提出了一个四维欧拉方程,通过分析发现保守混沌系统具有良好的遍历性,更适用于图像加密等领域.由于混沌系统对初始条件具有很强的敏感性,非常适用于图像加密中.近几年来,学者们也不断地去探究基于混沌系统的图像加密[15-17]算法,特别是基于保守混沌系统.刘静仪等[18]探究了位平面的数字图像加密算法和逻辑映射算法,发现具有良好的加密能力.Yildirim等[19-21]提出了一种新的混沌系统,利用图像密码学方法将其应用于图像加密.以上学者们分析了关于保守混沌系统的动力学特征以及应用,然而关于混沌系统是否能产生大量无限多共存类混沌吸引子还有待进一步探索.

为探究具有无限多共存类混沌吸引子的复杂动力学的保守混沌系统,本文提出了一个简单结构的四维保守混沌系统.结合广义哈密顿系统理论以及李雅普诺夫指数和分析,发现该混沌系统不仅仅是相空间体积上的保守系统,同时又是能量上的保守系统.分析系统的动力学特性,发现该系统具有大范围混沌特性.分别取能量函数中具有正弦函数、余弦函数以及正切函数时,可生成无穷多共存类混沌吸引子.由于该系统具有隐藏类混沌吸引子,不但遍历性好,而且安全性强,所以攻击者轻易不能恢复混沌系统,这样的混沌系统更加适用于图像加密中.因此进行了图像加密算法设计,分别通过对直方图、信息熵、密钥敏感性以及相关性的定量和定性分析,发现该算法具有很强的保密性.

1 新型混沌系统及保守性

广义哈密顿系统的结构[22]可以表示为

(1)

其中:X是系统的状态变量;U为输入;J(X)表示系统能量守恒部分,是一个反对称的结构阵;g(X)是输入增益向量;Y是系统输出;∇H(X)是哈密顿能量的梯度向量.

由于大多数具有实际性的耗散系统并不能应用该系统的结构,因此需在系统中加入耗散项R(X),由此可得:

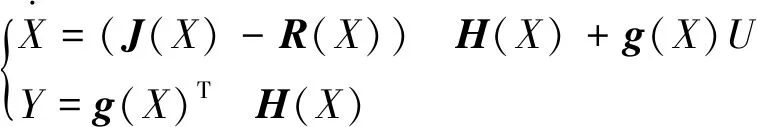
(2)

其中:R(X)表示系统的能量消耗.

根据文献[8],本文构造出一种新型的具有无限多类混沌吸引子共存的四维保守系统,系统模型如下:

(3)

其中:x、y、z、w为状态变量;a、b、c为系统参数.

根据系统(3)和广义哈密顿系统,可得:

对于能量交换的哈密顿能量可得:

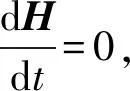
当给定参数值为a=4,b=2,c=2,初始值为(0.5,π,-0.5,-0.5)时,可得类混沌吸引子相图如图1所示.分析李雅普诺夫指数如图2所示.截取x-y平面,选取z=0,w=1,可得庞加莱截面图如图3所示.由此可得LE1=0.41,LE2=LE3=0,LE4=-0.41,由于李雅普诺夫指数和为零,这说明系统是体积保守混沌.由庞加莱截面图可以看出,系统处于混沌状态且相轨迹复杂,类似混沌吸引子.由于该系统是体积保守的混沌系统,不会吸引到附近的轨迹,因此系统不具有吸引子,从图1也可以看出,即可得类混沌吸引子,且系统的遍历性较好.

图1 类混沌吸引子相图

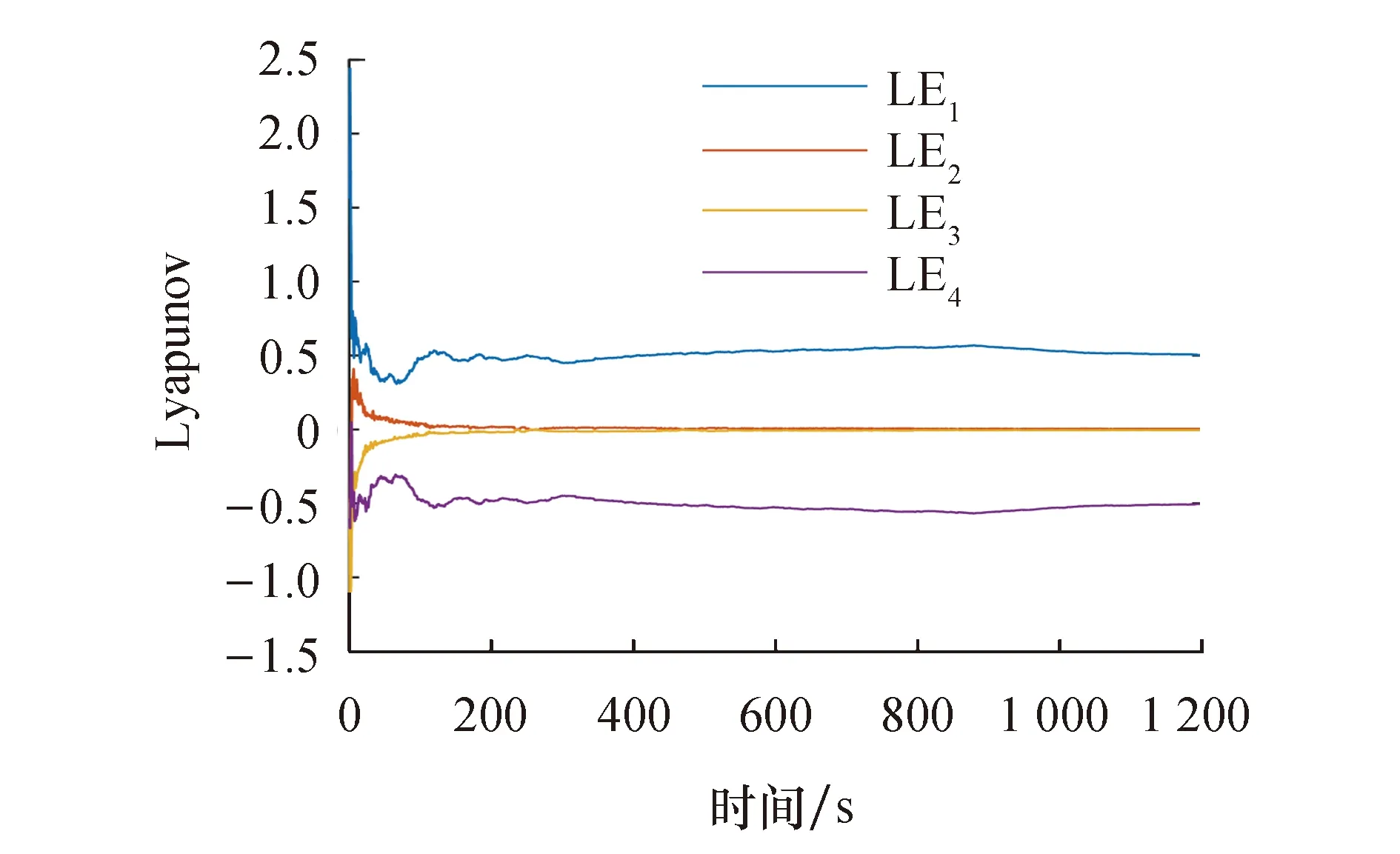
图2 李雅普诺夫指数

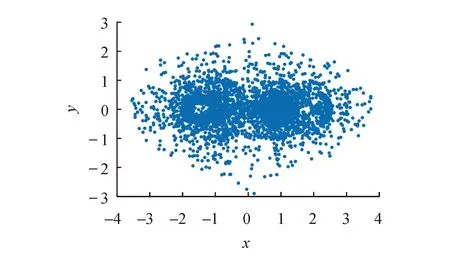
图3 庞加莱截面图

从上述分析可知,该保守混沌系统既是体积保守系统又是能量保守系统.

2 动力学分析及大范围混沌特性

根据(x,y,z,w)→(-x,-y,z,w)进行坐标变换,系统保持不变,由此可得到,该系统具有关于z-w平面的对称性.

分析系统的平衡点:

(8)

由式(8)计算可得系统是不存在平衡点的,那么该系统产生的类混沌吸引子均是隐藏的.

假设b=c=2,考虑参数a的值不同时研究系统的混沌特性.给定a∈[-2,10],初始值为(0.5,π,-0.5,-0.5),步长为0.1,得到如图4所示的李雅普诺夫指数图及指数和SLE.

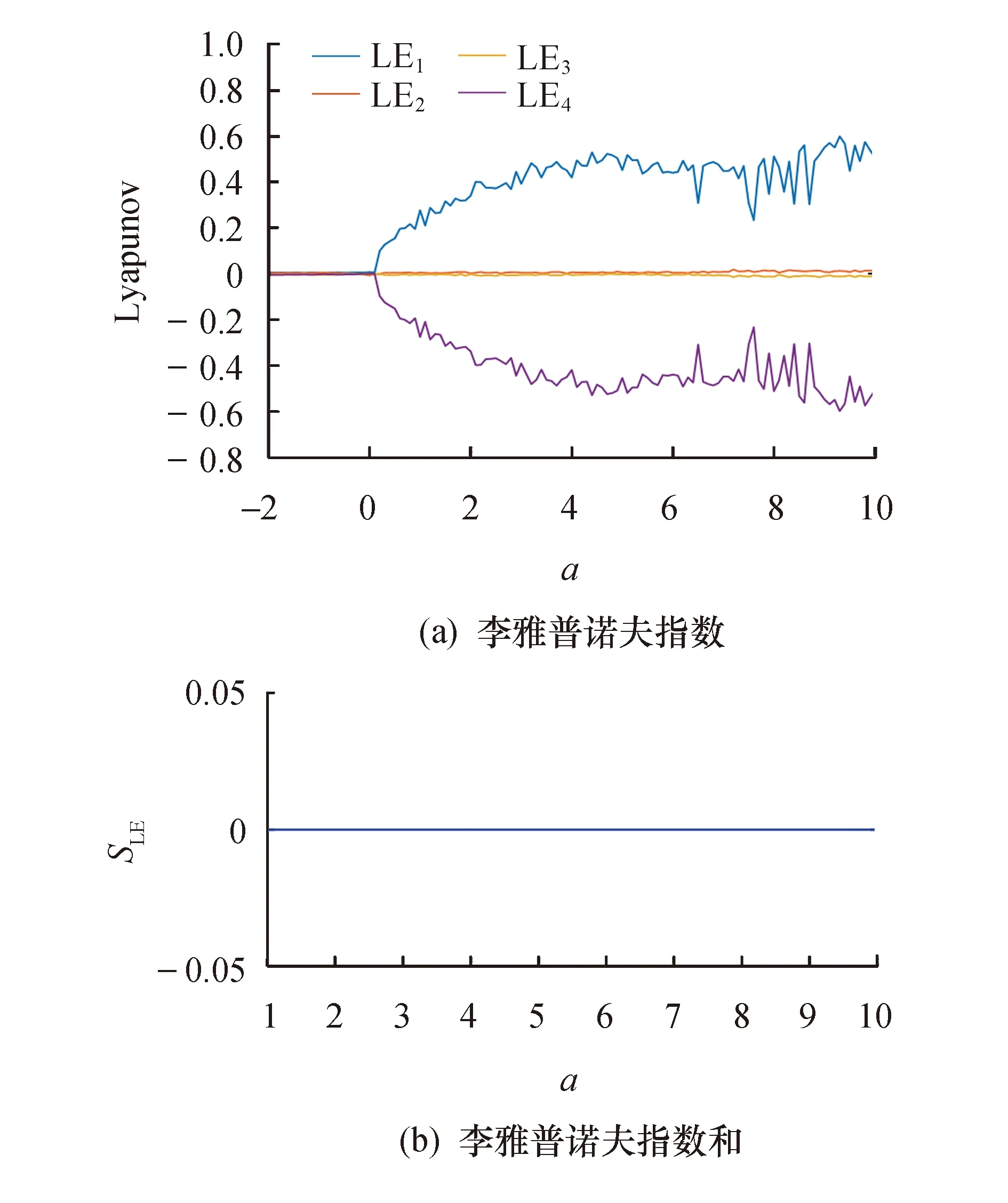
图4 李雅普诺夫指数分析(1)

由图4可以看出,系统是处于准周期和混沌状态的.当a∈[0,10]时,b=c=2, 系统处于混沌状态,李雅普诺夫指数和为0,此时系统是保守的.当a∈[-2,0]时,系统处于准周期状态.取a=-1时,可以得到准周期运动相图如图5所示.

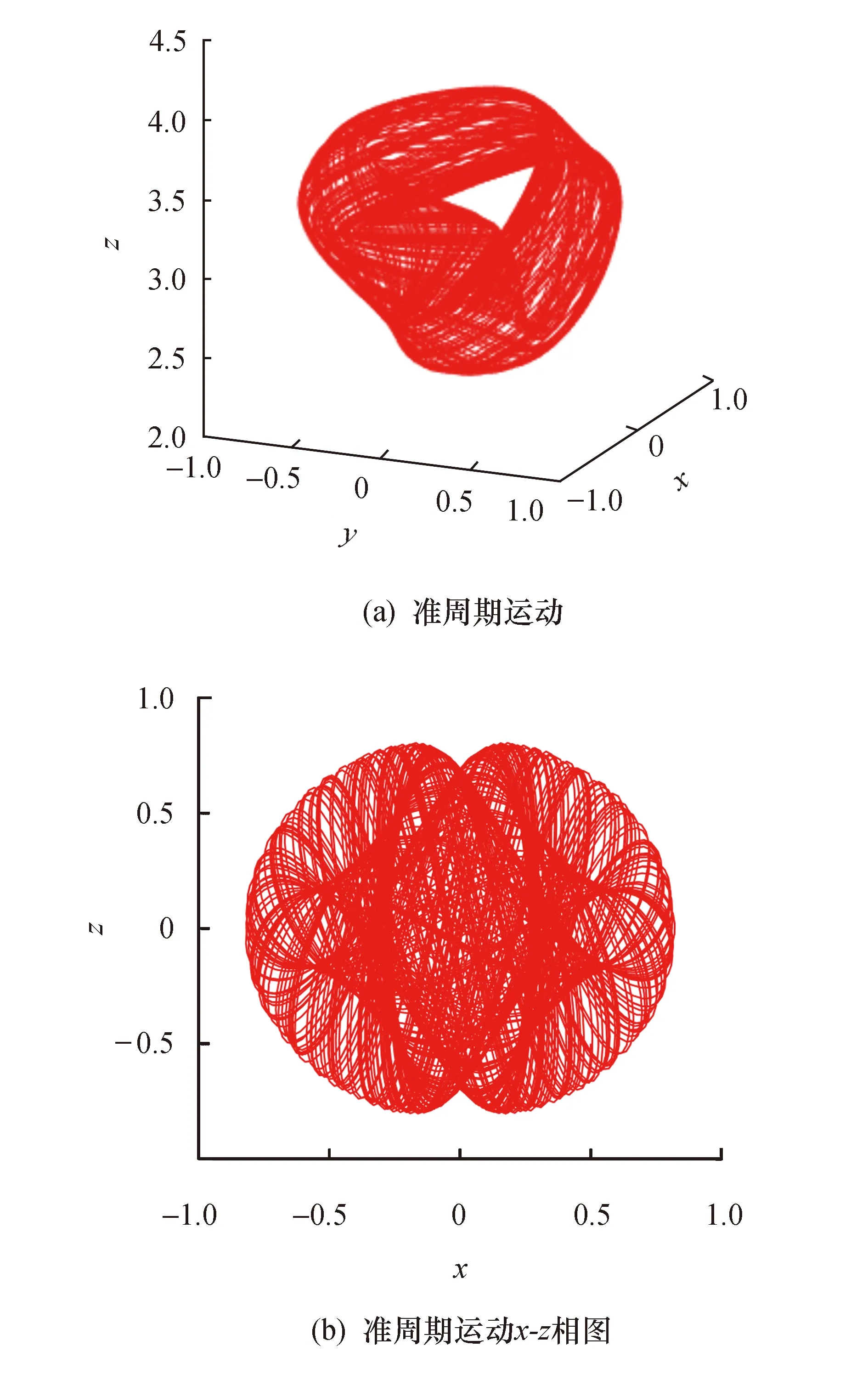
图5 准周期运动相图

当a∈[0,10]时,系统处于混沌状态,为进一步分析系统的混沌特性,得到关于a的分岔图如图6所示.根据分岔图可以看出,具有大量密集点区域,进一步说明系统是具有混沌特性的.那么,由于系统不存在平衡点,可以说明系统是具有隐藏类混沌吸引子的、既是空间上的又是体积上的保守混沌系统.

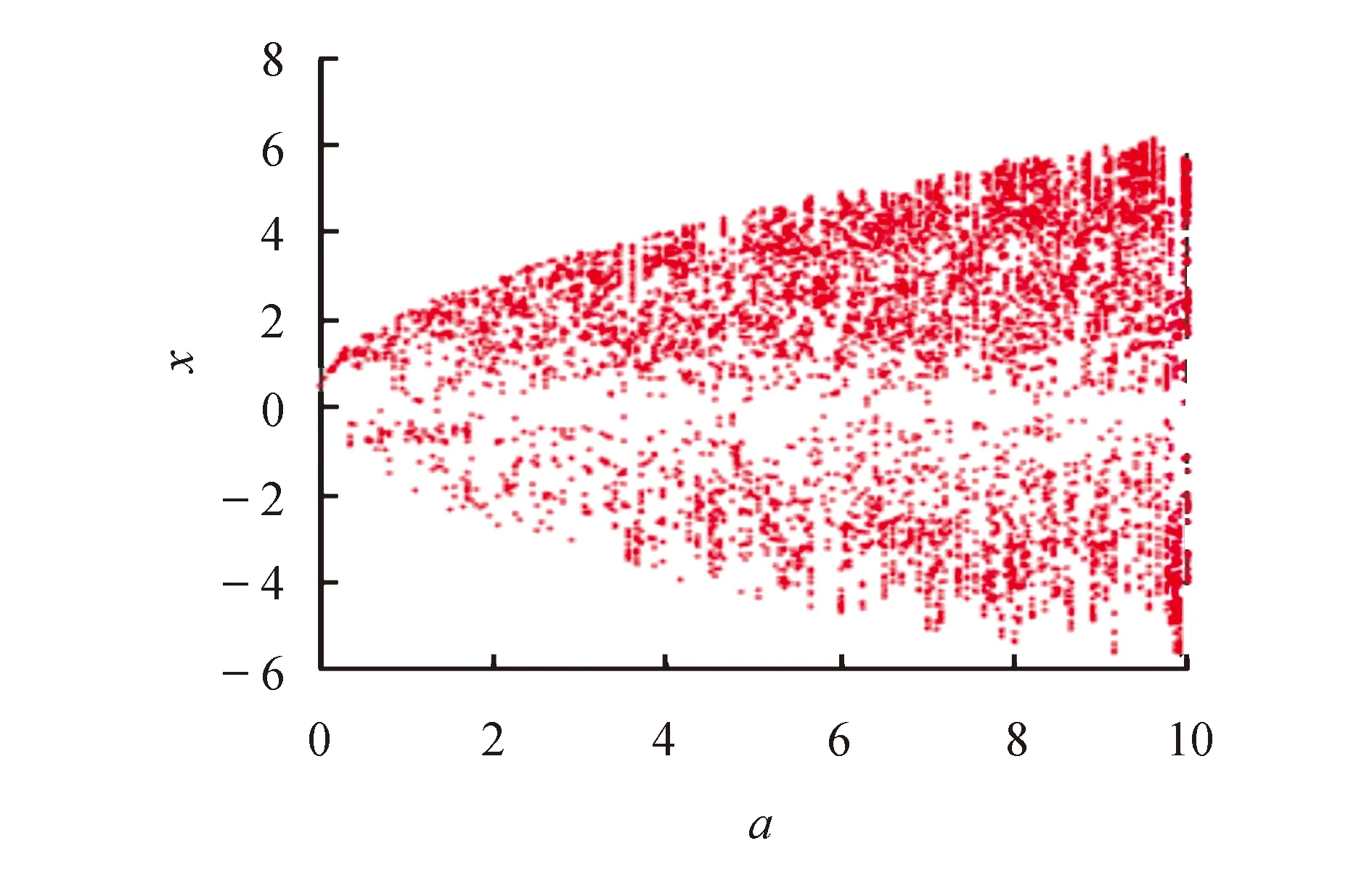
图6 分岔图

下面令b为控制参数,参数值为a=4,c=2,这里b∈[0,68],初始值为(0.5,π,-0.5,-0.5),分析系统的动力学特性,可以得到李雅普诺夫指数和指数和如图7所示.

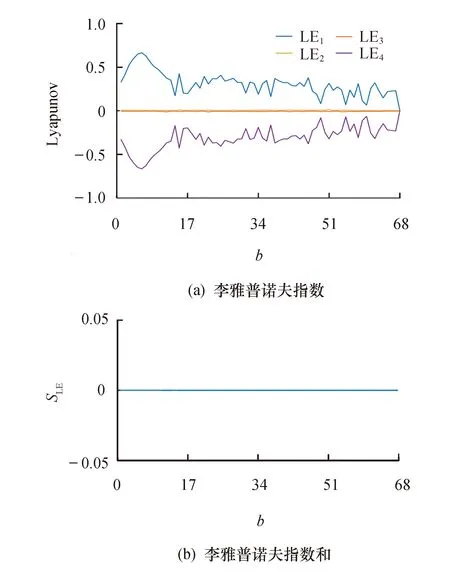
图7 李雅普诺夫指数分析(2)

根据李雅普诺夫指数分析可以得到,b∈[0,68]均属于混沌状态,且SLE为0,因此,可以说明系统在大范围内是属于保守的混沌系统.

3 无穷多共存类混沌吸引子

给定参数值a=4,b=2,c=2,初始值为(0.5,x0,-0.5,-0.5),x0=kπ,令k为控制变量,k取值为[1,50],分析初始值对系统的影响,可得分岔图、李雅普诺夫指数、指数和、时间序列如图8所示.

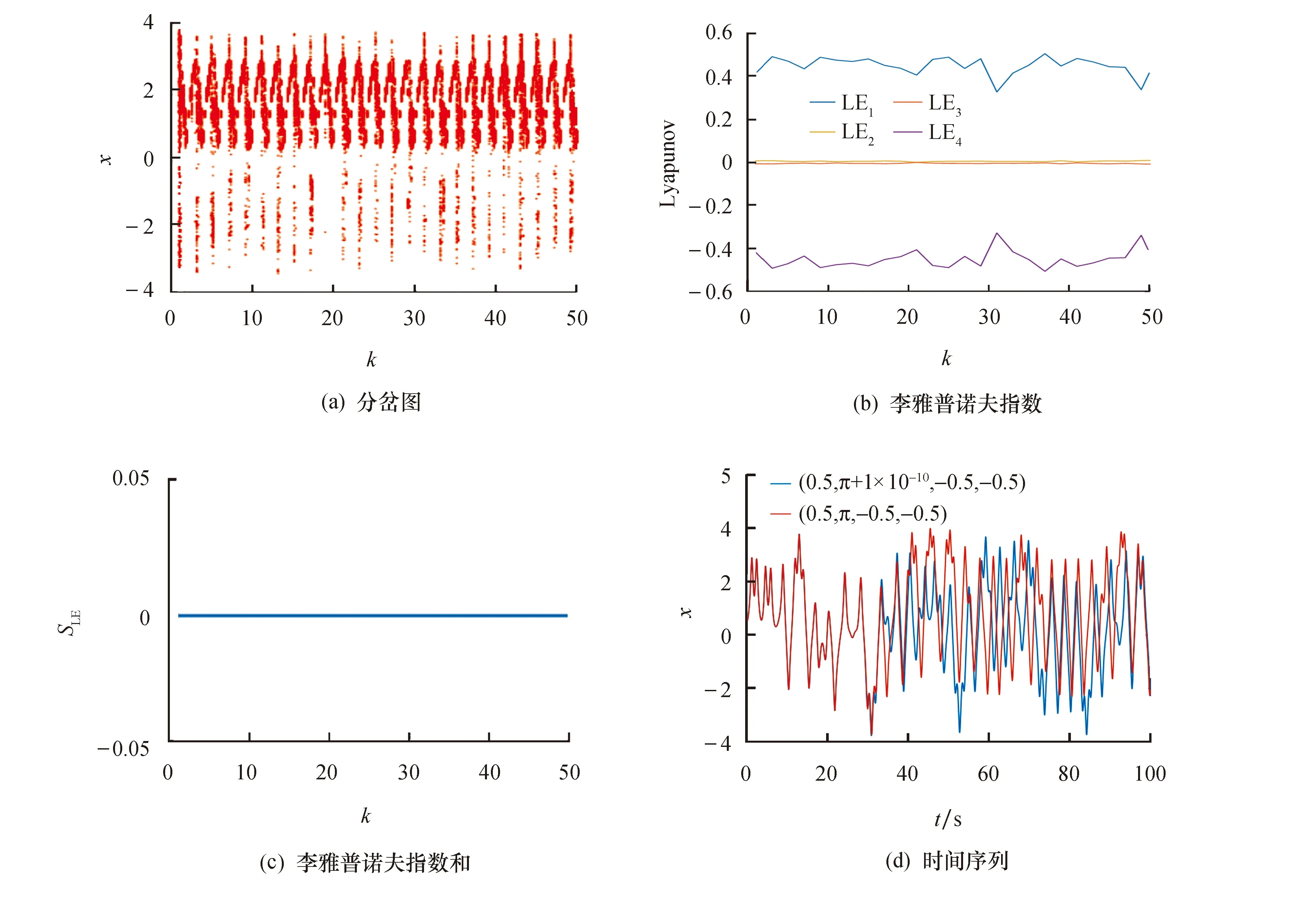
图8 控制参数k对系统的影响

由图8a分岔图分析可得具有均匀且大量密集点,表明系统是混沌的.同时,由图8b和图8c可得,李雅普诺夫指数含有一个正值,且李雅普诺夫指数和为0,这表明了系统是保守的.分析其初始值敏感性,给定初始值分别为(0.5,π,-0.5,-0.5)和(0.5,π+1×10-10,-0.5,-0.5),可以得到时间序列如图8d所示.通过对图8d分析可得,尽管初始值差距十分微小,经过数次迭代之后会产生不同的运动轨迹,因此可证明系统对初始值具有很大的敏感性.

由于∇H(X)中含有周期函数,因此系统存在含有类混沌吸引子共存现象的可能性,这里使∇H(X)=(x,af(y),z,w)T,其中f(y)可以表示为f(y)=sin(y)或f(y)=cos(y).

当f(y)=sin(y)时,令初始值为(0.5,kπ,-0.5,-0.5),其中k取值为-15,-13,-11,-9,-7,-5,得到类混沌吸引子共存如图9a所示;k取值分别为-1,1,3,5,7,9,得到类混沌吸引子共存如图9b所示;k取值分别为21,23,25,27,29,31,得到类混沌吸引子共存如图9c所示.可以看出系统分别在k值为负数、零、正数等不同条件下产生共存类混沌吸引子,这些类混沌吸引子虽然形状相似,但运行轨迹不同.

图9 f(y)=sin(y)时的类混沌吸引子共存

同理,在f(y)=cos(y)时,与以上初始值和初始条件相同,可得到图10的类混沌吸引子共存现象.从图中可以看出,f(y)=cos(y)中同样产生大量类吸引子共存,因此可以得出在参数值为a=4,b=c=2,初始条件为(0.5,kπ,-0.5,-0.5),k=1+2k0,k0∈Z的情况下,含有周期函数sin(y)及cos(y)均能够产生既是能量上保守又是体积上保守上的无穷多共存类混沌吸引子.同理,推导出周期函数tan(y)也可实现无穷多共存类混沌吸引子.

因此,在常见的三角函数中,包括余弦函数、正弦函数以及正切函数这种周期函数中,均能够产生无穷多共存类混沌吸引子.由此可推断,系统具有在f(y)为周期函数时产生无穷多共存类混沌吸引子的可能性.

4 图像加密

本节在提出的简单保守混沌系统的基础上,利用混沌信号进行加密与解密过程完全相同的混沌图像加密算法设计.该算法主要有五部分,包括密码生成、顺向扩散、旋转、置乱以及逆向扩散.因此,可得到基于保守混沌系统(3)的密码结构图,如图11所示.

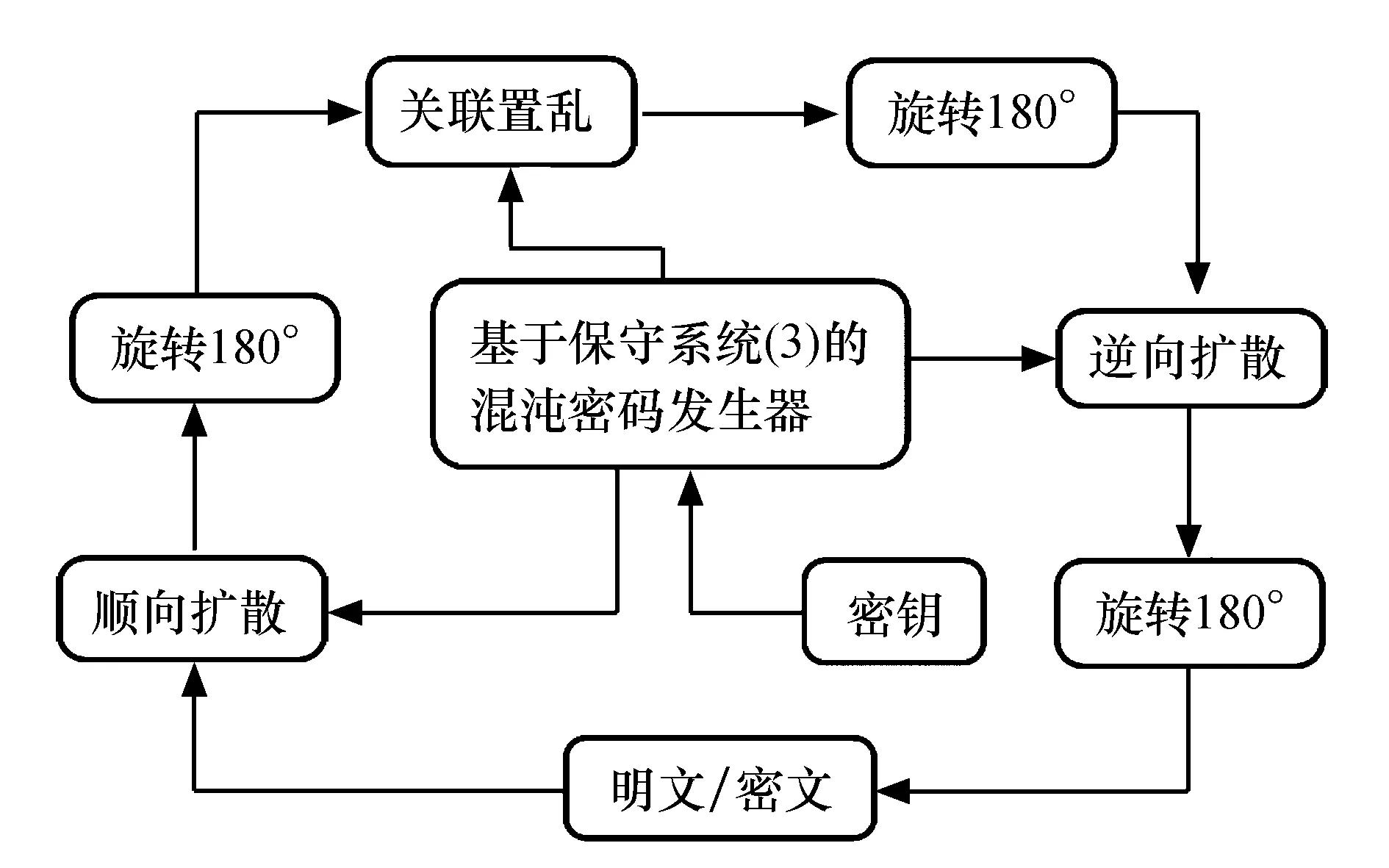
图11 基于保守系统(3)的密码结构图

这里设明文图像P是灰度为L比特的M×N大小的图像,要求满足mod(N,2)=0,如果不满足,则在明文图像的最后一列添加一个大小为M×1且元素均为0的列向量.

选取密钥为K={x0,y0,z0,w0,r1,r2},其中,{x0,y0,z0,w0}为保守混沌系统的初始值,而r1、r2为两个随机数.具体加密解密算法步骤如下.

步骤1,利用密钥K中的{x0,y0,z0,w0}作为系统(3)的初始值,通过龙格库塔法多次迭代,假设迭代次数为r1+r2+MN,这里去除掉过渡态r1+r2,仅保留MN次的数值,可以得到4个伪随机序列:{xi},{yi},{zi},{wi},i=1,2,…,MN.

步骤2,利用下式将序列{xi},{yi},{zi},{wi}依次生成伪随机矩阵A、B、C、D、E和F:

(9)

步骤3,利用异或运算和伪随机矩阵将明文P转换为矩阵V:

V(1,1)=P(1,1)XORA(1,1) XORr1

(10)

V(1,j)=P(1,j)XORA(1,j)XORV(1,j-1)

(j=2,…,N)

(11)

V(i,1)=P(i,1)XORA(i,1)XORV(i-1,N)

XORV(i-1,1) (i=2,…,M)

(12)

V(i,j)=P(i,j)XORA(i,j)XORV(i-1,j)

XORV(i,j-1)

(i=2,…,M;j=2,…,N)

(13)

步骤4,将矩阵A旋转180°得到矩阵T.

步骤5,利用矩阵C、D、E、F对T进行明文关联的置乱处理.如果mod(N,2)=0,则有

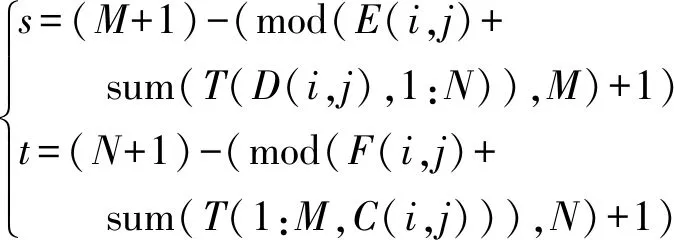
(14)

否则

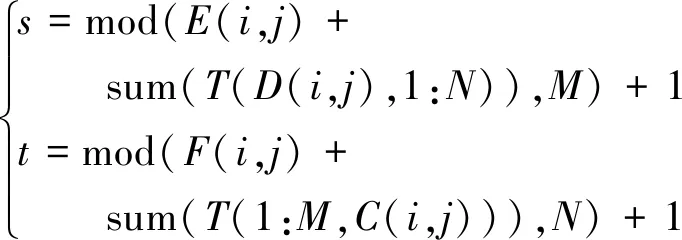
(15)

步骤6,如果s=i,或者是t=j,或者是s=D(i,j),或者是t=C(i,j),或者是D(i,j)=i,或者是C(i,j)=j这些情况时,保持T(i,j)的位置不变;否则,交换T(i,j)和T(s,t)的位置.

步骤7,重复步骤5和步骤6按照从左至右、从上至下的顺序依次去处理T中的每个像素点.

步骤8,将置乱后的矩阵T旋转180°得到矩阵L.

步骤9,利用按位异或计算,对矩阵L进行逆向扩散处理,转换为矩阵S:

S(M,N)=L(M,N)XORB(M,N)XORr2

(16)

S(M,j)=L(M,j)XORB(M,j)

XORL(M,j+1) (j=N-1,…,1)

(17)

S(i,N)=L(i,N)XORB(i,N)

XORL(i+1,1)XORL(i+1,N)

(i=M-1,…,1)

(18)

S(i,j)=L(i,j)XORB(i,j)XORL(i+1,j)

XORL(i,j+1)

(i=M-1,…,1;j=N-1,…,1)

(19)

步骤10,将矩阵S旋转180°可得到矩阵K,而K就是所得到的密文图像.

以上就是加密算法的全部步骤,解密过程是加密过程的逆过程.

5 仿真实验与性能分析

5.1 加密与解密

密钥为K={x0,y0,z0,w0,r1,r2},其中{x0,y0,z0,w0}为初始值,r1、r2为区间0到255内的随机整数.这里给定参数a=4,b=c=2,密钥x0,y0,z0,w0∈[-50,50],步长为1/l,l=1014,因此可得密钥空间为6.554×1052.仿真实验使用的计算机配置为:Intel(R) Core(TM)i5-9300H CPU @ 2.40 GHz,机带RAM为8.00 GB,系统类型是64位操作系统.在Matlab R2019b中编写并运行加密解密算法过程,这里选用经典的512×512 Baboon灰度图像进行仿真.在密钥空间内选取一组密钥K=[48.63,-10.78,15.55,43.0,180.0,8.0],可以得到图像加密与解密的明文图像、加密图像和解密图像如图12所示.

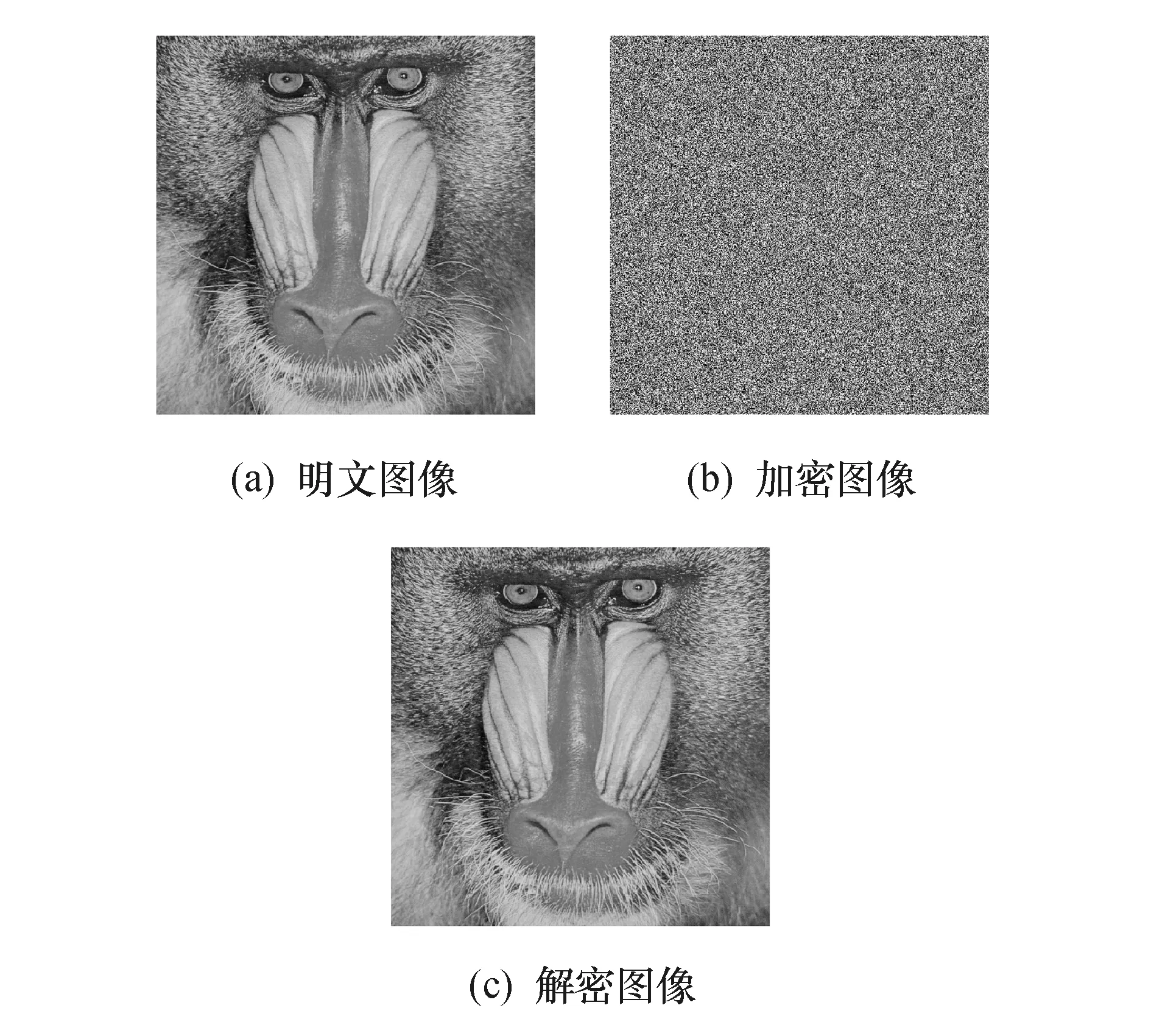
图12 图像的加密与解密

由图12可以看出,通过正确密钥进行加密与解密算法之后,解密图像与原图像完全一致,这表明该算法具有良好的加密和解密效果.

5.2 直方图与信息熵

通过直方图来分析加密算法的可视信息,进一步分析该算法保密性能是否良好,得到明文与密文的直方图如图13所示.

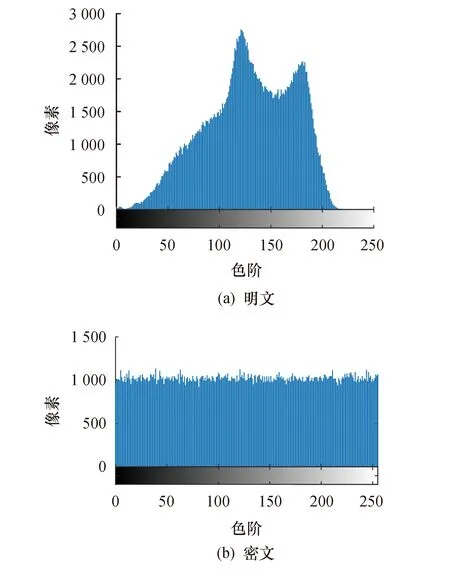
图13 直方图

由直方图可以看出,明文直方图起伏较大,而密文直方图较为平稳,通过定性分析说明可视信息较少,信息熵相对较大,也就是保密性较强,即安全性能较好.

进一步,进行信息熵计算可得Ha=7.358,Hb=7.999.理想的信息熵为8.000,文献[19]的密文信息熵为7.999,文献[20]的信息熵为7.986.因此通过定量分析可得,明文图像经过加密之后,该算法信息熵很高,可视信息较少,因此保密特性较好,具有良好的抵抗熵攻击的能力.

5.3 密钥敏感性

检验密钥的敏感性,首先通过定量分析,利用NPCR和UACI两个指标进行检测,其中NPCR是像素变化率,UACI是归一化平均变化强度.通过实验4次取平均值可得到表1的密钥敏感度分析结果.

表1 密钥敏感度分析

从表1可以看出,本文算法更接近于理论值,这说明算法对差分攻击的性能好,具有更强的抵抗攻击能力.

进一步,给定正确密钥有K0=[48.63,-10.78,15.55,43.0,180.0,8.0],在此基础上进行十分微小的变化,得到错误密钥有K1=[48.63,-10.78+1/l,15.55,43.0,180.0,8.0],同样选择512×512的Baboon灰度图像作为测试对象,可以得到密钥敏感性测试结果如图14所示.

图14 密钥敏感性测试结果

由图14分析可得,尽管密钥只是进行十分微小的变化,图像就完全解密不出来原明文图像,这说明密钥具有敏感性,且敏感性较强,只有完全正确的密钥才能解密出原图像.

5.4 相关性分析

图像的一个特征就是相邻像素具有很强的相关性,为了验证加密前后是否具有一定的相关性,这里在水平方向、垂直方向以及对角方向取10 000对像素点,通过定量分析可得相关系数计算结果如表2所列;定性分析可得相关性情况如图15所示.

表2 相关系数计算结果

由表2和图15可以看出,分别从定量和定性上分析可得,明文图像相关系数均大于0.7,且主要集中分布在对角线附近,这说明明文图像像素点之间具有较强的相关性.而密文相关性较小,甚至几乎为0,分布也较为均匀.这表明加密后这种较强的相关性被打破,图像的分布较为均匀与随机,体现了加密算法的合理性以及可实施性.

6 结论

本文结合广义哈密顿系统理论提出含有隐藏类混沌吸引子的简单四维混沌系统,该系统既是能量保守系统,又是体积保守系统.该保守混沌系统具有复杂的混沌动力特性,应用于图像加密领域具有良好的抵御外来攻击的能力.