基于改进的哈里斯鹰优化算法的特征选择

赵小强, 强睿儒

(1. 兰州理工大学 电气工程与信息工程学院, 甘肃 兰州 730050; 2. 兰州理工大学 甘肃省工业过程先进控制重点实验室, 甘肃 兰州 730050; 3. 兰州理工大学 国家级电气与控制工程实验教学中心, 甘肃 兰州 730050)

随着科学技术的不断发展与进步,在商业、科学研究以及社交媒体等领域都在不断地产生庞大而复杂的数据,与此同时,数据特征的维度也在不断增加.处理海量数据是当今数据挖掘中出现的一个具有挑战性的问题[1],即使技术在不断进步,机器学习也正面临着“维数灾难”的问题.由于需要大量的存储空间和计算时间,过高维度的数据会妨碍数据挖掘的过程[2].作为数据挖掘中数据预处理的关键,特征选择可以基于某种评价准则,在原始拓展空间中选择有助于输出的信息特征最佳子集来减少计算时间,以此来改善数据挖掘的性能[3].因此,如何研究特征选择问题并将其有效利用,成为数据挖掘当中的一项重点以及难点问题.

为了解决特征选择问题,研究人员提出一系列的特征选择方法.基于特征选择和学习算法结合方式的不同,可以将特征选择方法分为过滤式、嵌入式、集成式和包裹式四种类型[4].其中,过滤式的特征选择算法和学习算法互不相干,特征选择是后者的预处理过程;嵌入式算法可以将特征选择算法嵌入到学习算法中,特征子集随分类算法训练过程的结束而得到;集成式算法借鉴了集成学习的思想,通过训练多个特征选择算法,对比多个特征选择方法的结果,可以得到比单个特征选择方法更好的性能;包裹式算法可以将选用的算法包装成黑盒并通过它在特征子集上的预测性能评价特征子集,然后结合搜索策略获取最优子集[5].而在评估获得的特征子集的质量方面,包裹式算法通常会选择一种分类器来进行,例如K-近邻(KNN)、支持向量机(SVM)等.包裹式相较于过滤式可以获得性能更好的特征子集且效率高于嵌入式和集成式[4],包裹式主要包括启发式优化算法[6].

启发式优化算法是由研究人员受到自然物理现象的启发或模仿生物行为而提出用以寻求最优解的算法.其中,优化算法主要分为进化类、基于物理原理类和群智能类.进化类算法受到自然进化规律的启发,以遗传算法(genetic algorithm,GA)[7]为代表,搜索过程通过模拟生物进化过程来找寻最优解;基于物理原理的算法通过模仿宇宙物理规则找寻最优解,最为经典的算法为模拟退火(simulated annealing,SA)[8]和万有引力算法(gravitational search algorithm,GSA)[9]等;群智能优化算法基于模仿动物群体社会行为而来,最具代表性的算法为粒子群算法(particle swarm optimization,PSO)[10],其灵感来自于鸟类群体的搜索食物机制,个体值通过迭代来计算最优解.此类算法还包括灰狼优化算法(gray wolf optimizer,GWO)[11]、鲸鱼优化算法(whale optimization algorithm,WOA)[12]和樽海鞘优化算法(salp swarm algorithm, SSA)[13]等,尽管三类优化算法的机制不同,但搜索终值均为某域内最优解,在不同的领域中发挥着重要作用.嵇友迪等[14]通过设计响应全面试验,结合精英策略的非支配排序遗传算法对多目标优化函数进行优化求解,通过仿真验证汽车油箱托盘成形件质量得到改善;宋汶秦等[15]以风-光打捆发电系统为研究对象,模拟退火算法优化光热电站出力,有效降低了单位发电成本;朱昶胜等[16]提出基于改进果蝇算法随机森林回归模型用以风速预测,且经过实验证明了其模型具有更高的预测精确度.

近年来,启发式优化算法凭借自身的优势,在特征选择上受到广泛关注.研究人员开始将二者结合以提高分类精度.Emary等[11]提出了灰狼优化算法的二进制版本并将其应用在特征选择中,相较于传统算法,有效地提高了分类精度.Tawhid等[17]提出了基于粗糙集的鲸鱼优化算法的二进制版本,并在C4.5等分类算法下验证了其优越性.Mafarja等[18]提出了三个版本的二进制蚱蜢算法并应用于特征选择问题,使用经典UCI数据集进行实验且效果良好.李郅琴等[19]基于黑寡妇算法开发了其二进制版本以此进行特征选择,分别在回归、分类等方面验证其优越性.然而,元启发式优化算法本身具有易陷入局部最优、早熟收敛等问题,并且由于包裹式特征选择所选取的特征子集的性能对学习算法依赖度高,因此算法性能优劣也决定了特征选择的子集性能的好坏.

以上优化算法在特征选择中的应用表明,使用元启发式优化算法进行特征选择可以灵活地利用智能优化机制自身的探索能力.每种算法根据自身的工作方式所控制的标准来随机地生成特征子集,并且已被证明[20]它们可以有效地帮助减少执行时间并获得准确结果.但由于特征选择问题的复杂性,将单一的优化算法仅进行二进制改进很难取得更好的效果.根据No-Free-Lunch定理[21]可得,没有一种优化算法可以解决所有的优化问题,若想要将优化算法具体应用在某一特定问题,需要对优化算法进行二次改进或优化.

综合上述分析,本文主要对哈里斯鹰优化算法[22]进行改进,并将其应用于基于KNN分类器的包裹式特征选择问题中.首先对哈里斯鹰优化算法后期种群多样性减少和易陷入局部最优的问题,引入混沌映射以及高斯变异来对其进行改进,提出了混沌哈里斯鹰优化算法,并分别设计哈里斯鹰优化算法和混沌哈里斯鹰优化算法的二进制版本,将二者应用在基于KNN分类器的包裹式特征选择问题中.通过对经典的UCI数据集进行测试,并与其他已有的特征选择算法进行对比,本文所提算法在求解精度方面有显著提升.

1 相关理论

1.1 哈里斯鹰优化算法

哈里斯鹰优化算法(HHO)[22]是以哈里斯鹰的捕猎行为为基础进行模拟,于2019年提出的启发式优化算法.HHO将鹰群捕猎行为分为全局探索阶段、由全局探索阶段向局部开发阶段转换和局部开发阶段三个部分,并且局部开发阶段展示出4种围攻策略,其流程图如图1所示.

图1 HHO算法流程图

1.1.1全局探索阶段

在HHO中,每只哈里斯鹰都被认为是候选解,并且在每次迭代中最优解被认作为预期的猎物位置.哈里斯鹰随机栖息在某些位置,并根据两种策略来等待并发现猎物,该阶段哈里斯鹰的位置X更新如下式所示:

(1)

其中:X(t+1)表示下次迭代中鹰的位置向量;Xrabbit(t)表示兔子的位置;X(t)表示当前老鹰的位置;r1、r2、r3、r4和q为在(0,1)的随机数,r3为缩放系数,用以进一步增加规则的随机性,r4取接近1的值;UB、LB表示变量的上界与下界.当q≥0.5时,老鹰随机栖息在高大的树木上(群体家庭范围内的随机位置);当q<0.5时,老鹰则依据其他家庭成员以及可攻击的兔子位置来栖息.鹰群的平均位置如下式所示:

(2)

其中:N为鹰群总数;t为当前迭代次数.

1.1.2由全局搜索向局部开发阶段转换

HHO算法根据猎物所剩的逃逸能量,从全局搜索向局部开发转化.在逃跑过程中,猎物的能量显著降低.令E表示猎物的逃逸能量,E0为其能量的初始状态,在(-1,1)中随机变化,现将这一事实模拟如下式所示:

E=2E0(1-t/T)

(3)

在500次迭代中E的变化如图2所示.

图2 E的迭代变化

在HHO中,当逃逸能量|E|≥1时,鹰群搜索不同区域以探索兔子的位置,此时哈里斯鹰处于全局搜索阶段;当|E|<1时,鹰群转向局部开发阶段.

1.1.3局部开发阶段

在此阶段,鹰群针对不同的情况展示了4种不同的捕猎策略.根据猎物的逃离威胁的情况,设r为猎物在突袭前成功逃离(r<0.5)或者未逃离的机会,此时结合猎物逃逸能量E,进行不同围攻策略,具体如下:

1) 软围攻:当r≥0.5且|E|≥0.5时,鹰群发动软围攻,其位置更新如下式所示:

(4)

其中:ΔX(t)为兔子在迭代次数t中的位置向量与当前位置向量的差值;J为每次迭代中用以表示兔子运动性质的随机变化的数值.

2) 硬围攻:当r≥0.5且|E|<0.5时发动硬围攻,位置更新如下式所示:

X(t+1)=Xrabbit(t)-E|ΔX(t)|

(5)

3) 渐进式快速俯冲的软围攻:当r<0.5且E≥0.5时,兔子有足够的能量逃脱,鹰群发动渐进式快速俯冲的软围攻,其位置更新如下:

(6)

(7)

其中:LF(x)是为了模拟兔子逃跑阶段的欺骗性运动而引入的莱维飞行策略;μ、ν为(0,1)内的随机值;β为1.5的默认常数值.

4) 渐进式快速俯冲硬围攻:当|E|<0.5且r<0.5时,兔子已经没有足够的能量逃跑,鹰群在此时构筑硬围攻捕捉并且杀死猎物,位置更新如下:

(8)

(9)

1.2 混沌映射

作为自然界当中常见的非线性现象,混沌因其随机性、长期不可预测性和规律性,经常被研究人员应用于优化搜索问题[23].经过实验证明,混沌映射对优化算法而言有利于其保持种群多样性,且有可以帮助算法跳出局部最优和改善其全局搜索的能力.常见的混沌映射有Logistic映射和Tent映射,而单梁等[24]通过研究表明,Tent映射的遍历性和收敛速度均优于Logistic映射,其数学表达式如下式所示:

(10)

1.3 高斯变异

高斯变异是自遗传算法改进而来,旨在进行变异操作时用一个服从均值为μ、方差为σ2的正态分布的随机数来代替原本的参数值[25],其变异公式如下式所示:

Xbest(t+1)=X(t)(1+N(μ,σ2))

(11)

其中:Xbest(t+1)为变异后个体的位置.

由正态分布的特性可得:高斯变异的重点搜索区域为原个体附近的局部区域,不仅提高了算法的鲁棒性,还有利于增强算法的局部搜索能力,使得算法可以高效地寻找全局最小值点.

2 基于改进的哈里斯鹰算法的特征选择算法

哈里斯鹰优化算法参数较少,原理简单且全局搜索能力强,但其存在收敛速度较慢、种群多样性减少、易陷入局部最优等缺陷[26].本文针对这些问题进行改进,并将改进后的算法称为混沌哈里斯鹰算法(CHHO).

2.1 混沌哈里斯鹰优化算法

针对提及的HHO算法在后期种群多样性减少的问题,本文引入混沌映射,将HHO算法当中初始逃逸能量E0和逃逸能量E进行更新,以保证HHO在全局探索阶段拥有足够的种群多样性.令β=0.5,其逃逸能量公式更新如下:

引入高斯变异算子可以有效避免算法陷入局部最优,本文设以一定的概率p对当下最优解X(t)进行高斯变异.此外,借鉴“贪婪选择”的思想,实行优胜劣汰的选择规则,将种群最优位置更新如下式所示:

(14)

其中:Xbest(t+1)为变异后的个体位置;p为优胜劣汰选择概率.使用该选择策略,可以有效提高算法的搜索效率.

2.2 针对特征选择问题的CHHO算法的二进制策略

目前元启发式优化算法有许多种类,不同种类的适用范围不同,但基本可以分为数值型和离散型两类.在传统的HHO算法中,鹰群不断在连续空间内搜寻最优解,而针对特征选择问题,本质是在离散的二进制空间找寻最优解.离散型问题应用连续型算法需要进行编码和解码,在特征选择问题中,则需要引入二进制编码,即在此问题中,解决方案被定义为一维向量,其中向量的长度为原始数据集中的特征数量并随机使用“0”或“1”初始化每一个特征,“0”代表该特征没有被选择,“1”代表该特征被选择,使用下式即可将连续值映射到二进制值:

(15)

其中:Zmn为解向量的离散形式.图3为CHHO在特征选择问题中的示例.

图3 特征选择中的CHHO示例

2.3 基于CHHO算法的优化特征选择模型

本文使用CHHO的二进制版本进行分类问题的特征选择.在特征选择中,对于一个特征数为N的数据集,其特征子集的组合具有2N种情况,这是一个巨大的特征选择空间,需要使用二进制的CHHO在特征空间自适应搜寻特征子集组合.最佳的特征子集组合应是具有最大分类性能和最少特征选择数量的组合,在算法迭代过程中,通常选用适应度函数来评判每个解的质量,CHHO算法将分类的准确性以及特征子集作为指标,故用于评估CHHO在特征选择问题的适应度函数[27]如下式所示:

(16)

其中:ER(D)为分类的错误率,其表达式如下:

ER(D)=1-Accurcy

(17)

其中:R为所选特征子集的长度;C为特征长度;α为分类的精确性,通常α∈(0,1);β为所选特征在适应度函数中所占的权重,在本文中,取α为0.99, 且β=1-α.

KNN算法是一种简单且常用的分类方法,作为一种监督学习方法,其精度高,对异常值不敏感.它事先了解存有标签的样本数据与所属分类的对应关系,当没有标签的新数据被输入后,算法将新数据的每个特征与原样本集中的数据特征进行比较,然后提取样本集中特征最相似(最近邻)的分类标签.因此,在该特征选择模型中,使用KNN算法进行分类以确保所选特征的优良性.在CHHO中,使用KNN分类器(其中K=5)建立包裹式特征选择模型,以评估CHHO选定特征子集的质量.

本文提出的基于CHHO的特征选择模型流程图如图4所示.

图4 CHHO特征选择流程图

3 实验与结果分析

3.1 实验设置

为了验证算法CHHO在基于KNN分类器的包裹式特征选择问题中的有效性,本文采用UCI数据库中的18个经典数据集进行实验,数据集在维度和样本数量上的不同代表着实际应用中的不同问题.对每个数据集,以交叉验证的方式将其分为三个不同的部分,即训练集、验证集和测试集.每个数据集的特征个数、样本数的详细信息如表1所列.

表1 UCI经典数据集

在本文实验中,为了保证实验的客观全面,本文还选取了已经应用于特征选择的优化算法用作对比,分别是灰狼优化算法(GWO)[11]、遗传算法(GA)[28]、粒子群算法(PSO)[29]以及未优化的哈里斯鹰优化算法(HHO),其具体参数:种群大小为8,迭代次数为70,维度为数据特征数量,搜索域为[0,1],重复运行次数为20,GA交叉概率PC=0.8,PSO惯性因子ω=0.1,适应度函数中的α=0.99,适应度函数中的β=0.01.

为保证公平的原则,本文实验均在AMD Ryzen 7 5800H CPU@3.20 GHz的运行环境下,使用Python3.8进行,每次实验都重复20次,以验证其稳定性.

为验证本文提出算法在特征选择过程中的优化效果,本文使用如下指标来评估算法性能:

1) 平均分类准确率:描述给定所选特征集的分类准确度的平均值,用下式表示:

(18)

其中:M为算法运行次数;acc(i)为第i次的分类准确率.

2) 平均适应度Average:描述算法在运行时,计算所得的适应度平均值,用下式计算:

(19)

3) 最佳适应度值Best:描述在20次算法运行时,所得适应度的最佳值.

4) 最差适应度值Worst:描述在20次算法运行时,所得适应度的最差值.

5) 平均所选特征个数Avg selected:描述算法在特征选择问题中所选特征子集个数的平均值,用下式表示:

(20)

6) 适应度标准差(std):描述算法在M次实验中所体现的稳定性能力,标准差越小说明算法的稳定性越好,表达式为

(21)

3.2 实验结果与分析

表2为对比算法20次运行获取的适应度函数的平均值,可以看到,本文所提出的CHHO算法对于适应度函数的平均值能够在绝大多数低维、高维数据中表现出良好的性能,也验证了CHHO算法相较于其他算法具有更好的自适应搜索特征空间的能力.同时,类似的结果也可以从表3和表4中看到,表3和表4表示所有运行次数中获得最佳与最差的适应度函数值.

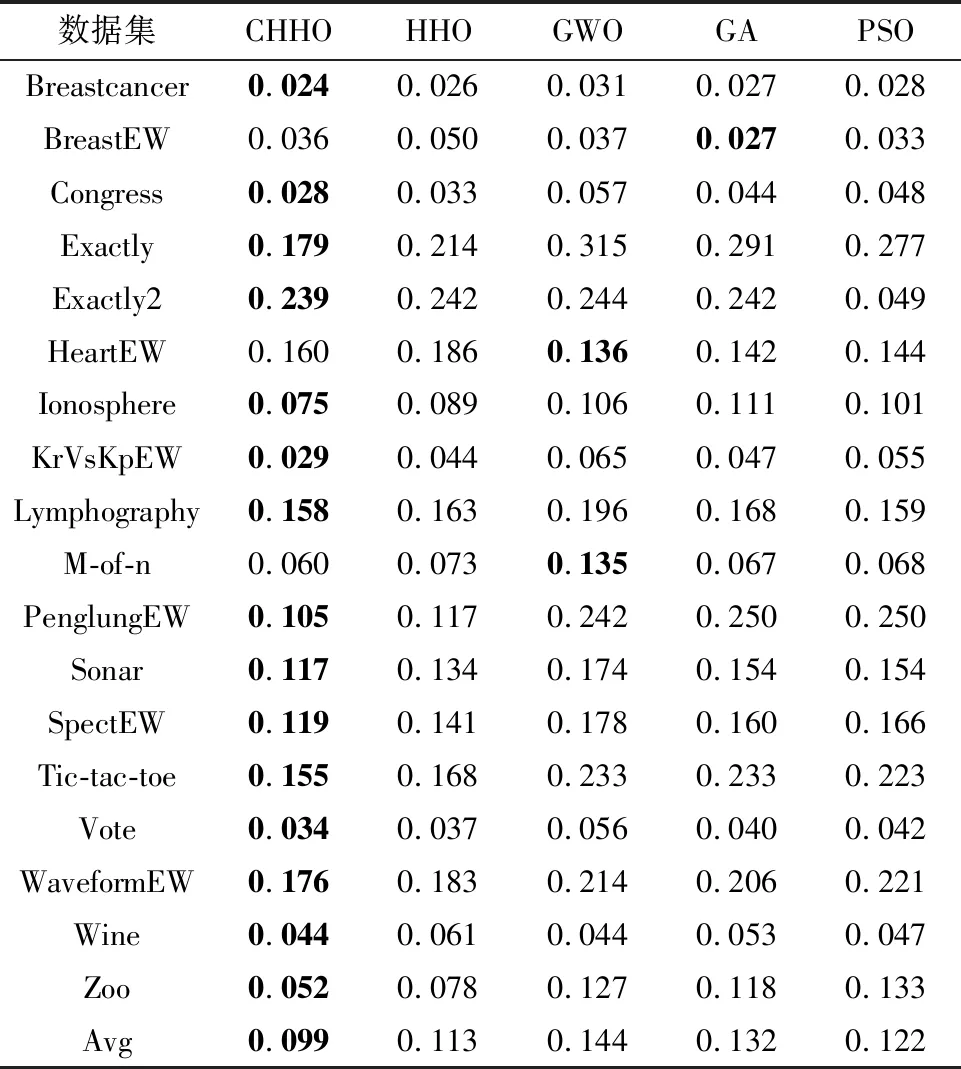
表2 各算法适应度函数平均值

表3 各算法适应度函数的最佳值

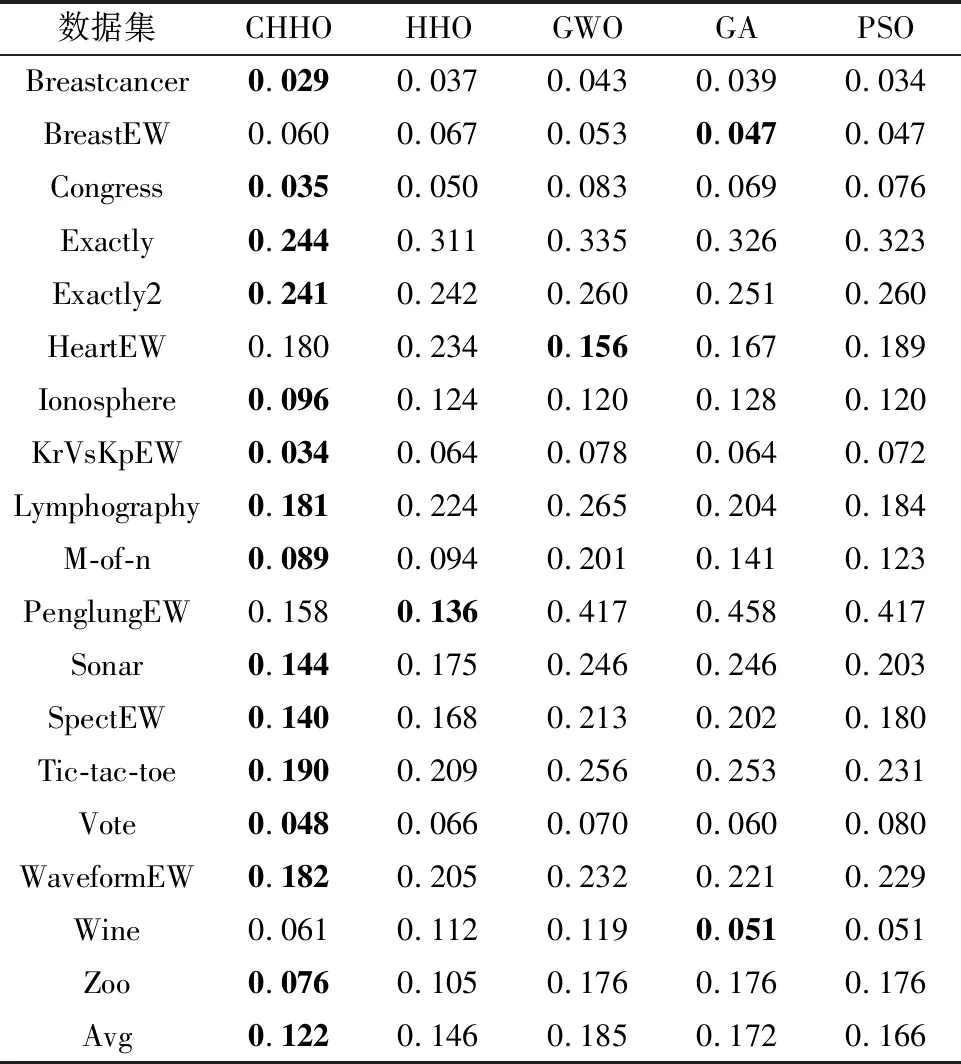
表4 各算法适应度函数的最差值

表5表示了所有运行次数中各个算法对于适应度函数的标准差,用以描述算法的鲁棒性和可重复性.可以看出,CHHO在大部分数据集中性能不仅明显优于GWO、GA以及PSO算法,而且相较于HHO算法性能提升显著,这表明了该算法具有鲁棒性和可重复性达到最优的能力.

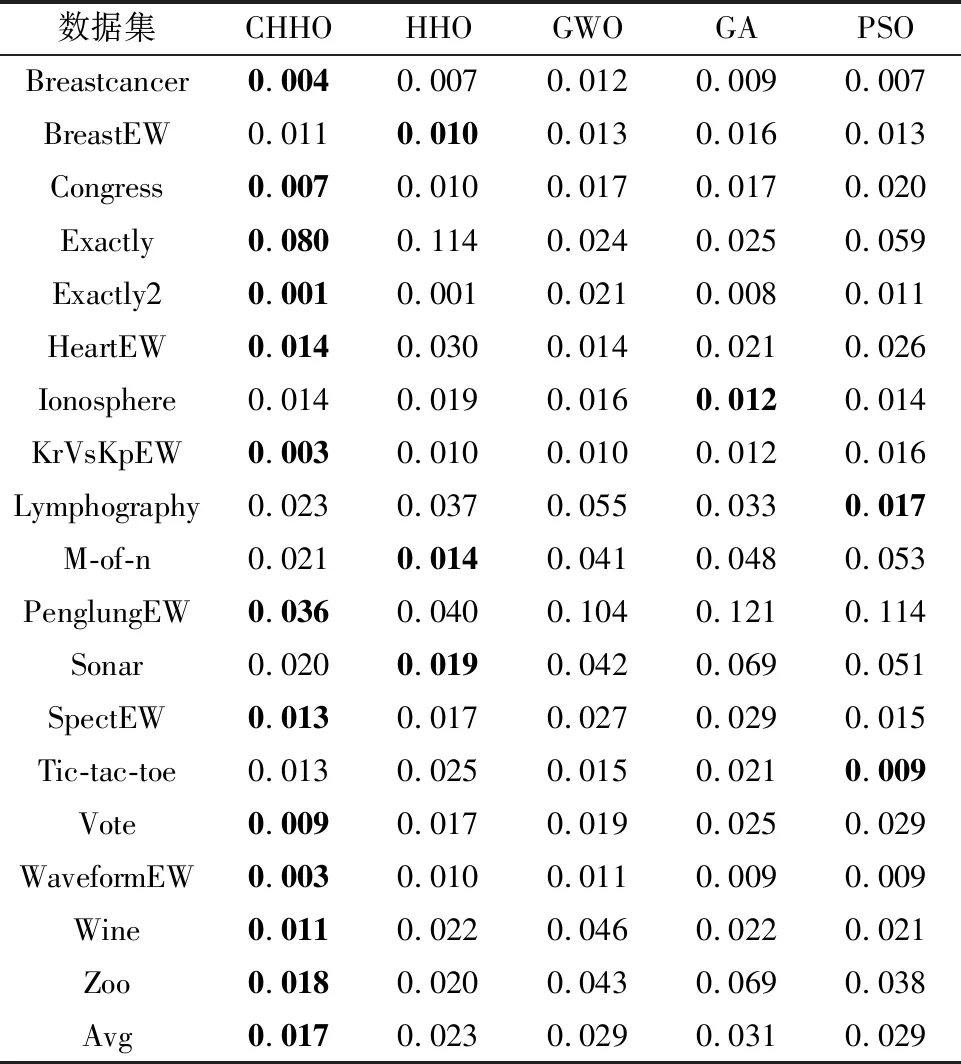
表5 各算法适应度函数的标准差

根据表6所示的分类精度实验结果可以看出CHHO算法的性能,在平均分类精度这一指标上除Breastcancer和Exactly2数据集外,CHHO算法的性能优于GWO、GA、PSO等算法,并且相较于HHO算法,分类准确度平均提升了2.1%.虽然在Breastcancer和Exactly2数据集中的表现未达到最优,但其表现的性能在五种算法中可以达到次优,这表明该方法能够针对不同维度的数据进行有效分类.因此可得,本文所提的CHHO算法在基于KNN分类器的包裹式特征选择问题中具有明显竞争力.

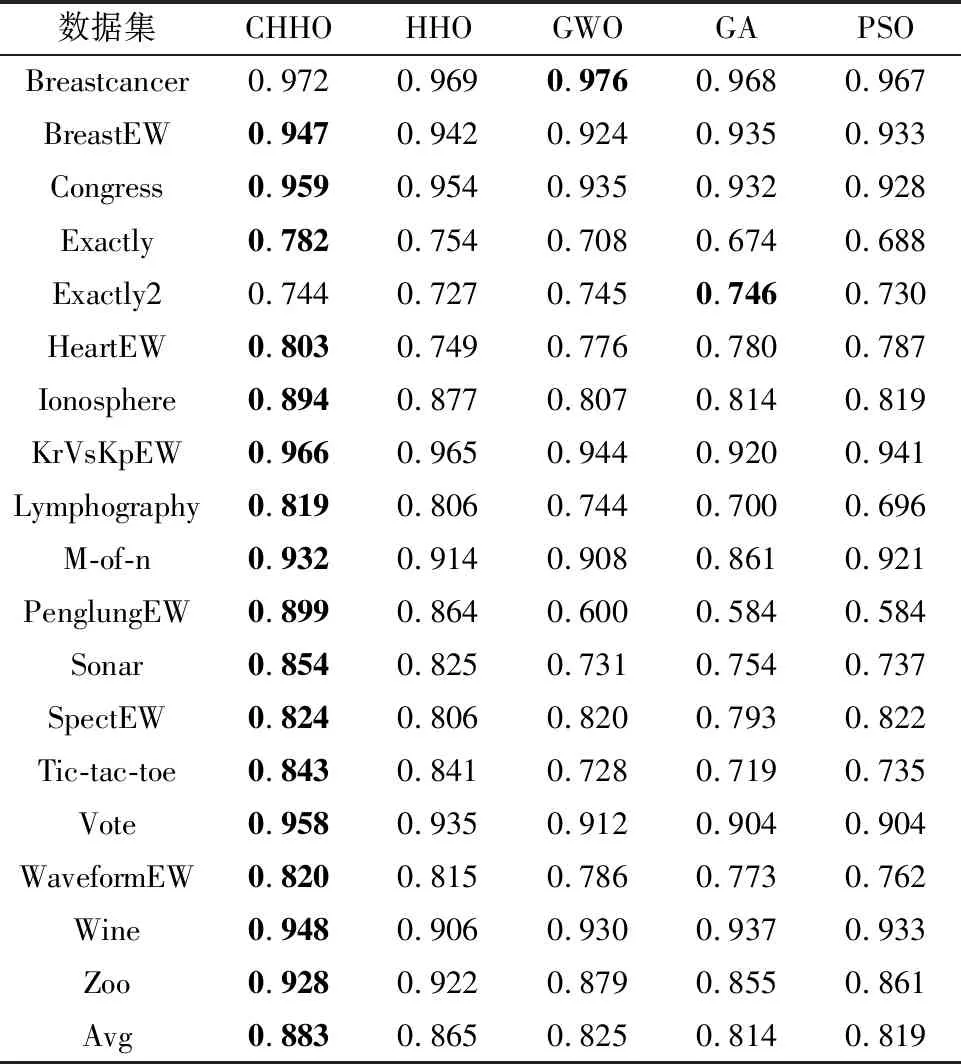
表6 各算法的平均分类准确率比较

表7是对不同数据集所选择特征个数的平均值.如表7所示,CHHO算法平均特征选择数为7.67个,相较其余4种优化算法特征选择数明显减少,这表明在大多数情况下CHHO都可以选择相对较少的特征,尽管在BreastEW、KrVsKpEW等数据集中未得到最优的结果,但在大部分数据集中的表现达到了最优,并且相对于HHO算法而言,改进效果明显.因此,相对于对比算法而言,本文所提算法在数据降维问题上具有明显优势.

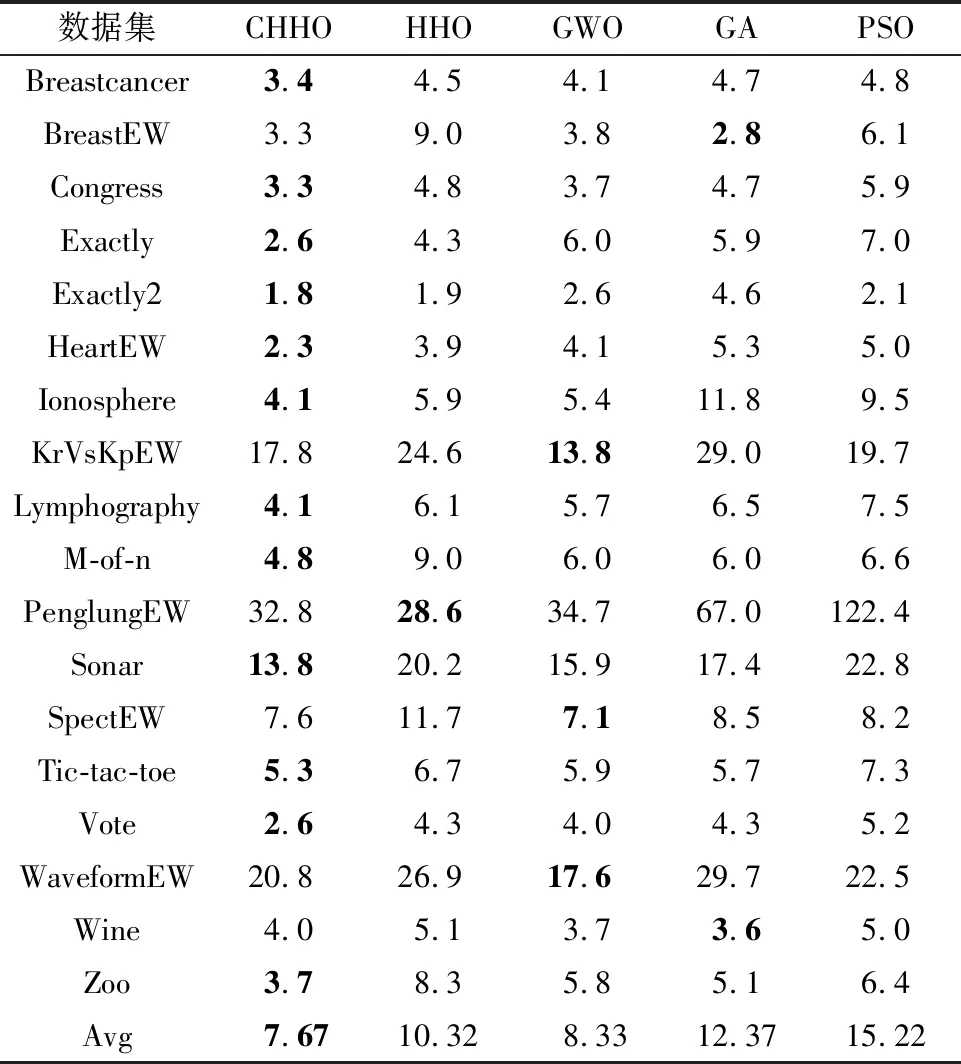
表7 各算法所选特征平均数

同时,图5是将所有数据集的最佳、平均和最差适应度值作平均,从图中可以得出,CHHO的性能明显优于对比的4种优化算法.图6及图7是对所有数据集的分类精度的平均值以及选取特征个数的平均值的比较结果,可以看出,CHHO所选特征个数为5种算法中最少的,并且在此基础上,CHHO可以达到最高的平均分类准确率,因此,CHHO可以在选择较少特征个数的情况下得到良好的分类性能.

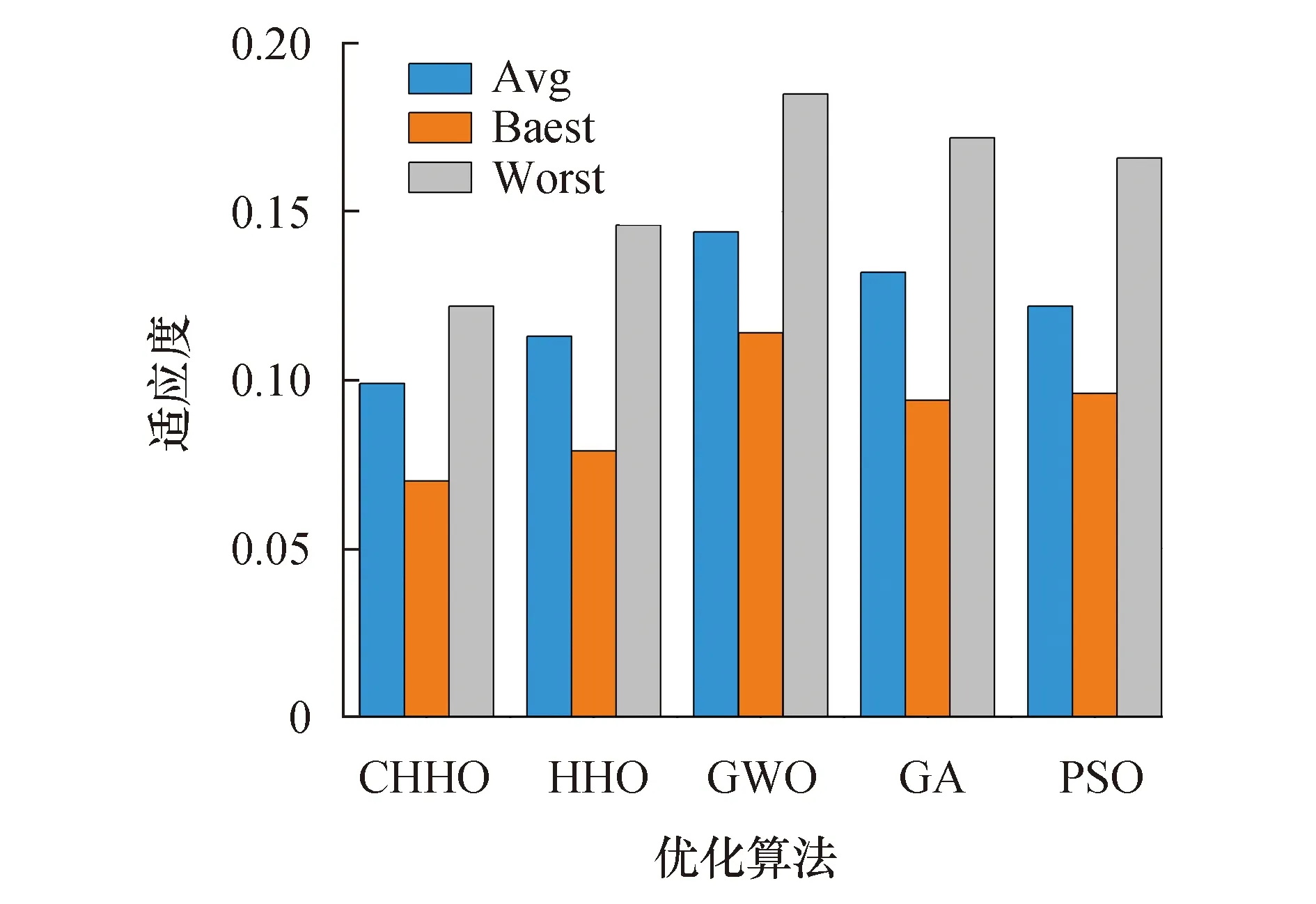
图5 对所有数据集的适应度最佳、最差和平均值

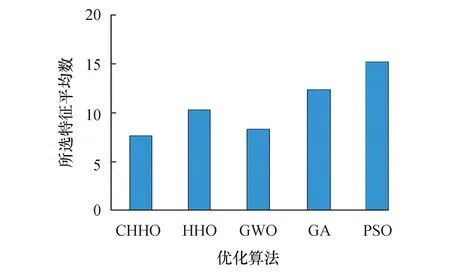
图6 对所有数据集的分类精度平均值

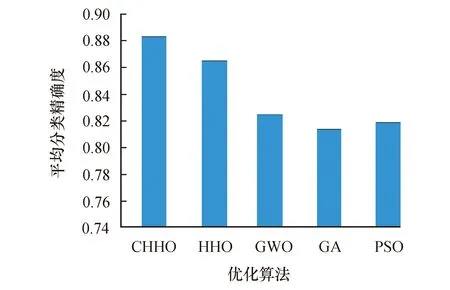
图7 对所有数据集的特征选择个数平均值

4 结论

本文首先针对传统的哈里斯鹰优化算法种群多样性减少、易陷入局部最优等缺陷,第一步引入混沌映射来增加种群多样性,第二步引入高斯变异等策略来避免其陷入局部最优;其次将本文所提CHHO算法进行二进制转化并应用于基于KNN分类器的包裹式特征选择问题中.通过对经典UCI数据集进行分类,并与HHO、PSO、GWO、GA等优化算法进行比较,本文所提的CHHO算法在寻求特征子集方面具有显著优势.

由于特征选择可以有效地改善不平衡分类中过采样所引起的过拟合现象,故未来研究将本文提出的算法与过采样算法相结合,使其可以应用到不平衡数据分类的问题中.