数值界不确定直流微电网的鲁棒H∞控制

王晓兰, 陈 爽

(1. 兰州理工大学 电气工程与信息工程学院, 甘肃 兰州 730050; 2. 兰州理工大学 甘肃省工业过程先进控制重点实验室, 甘肃 兰州 730050; 3. 兰州理工大学 电气与控制工程国家级实验教学示范中心, 甘肃 兰州 730050)

微电网主要由分布式电源、储能装置、变换器和交直流负荷等单元组成,与大电网之间通过静态开关可以实现并网运行,也可以孤岛模式运行[1-2].根据母线电压类型不同,微电网分为直流微电网、交流微电网和混合(交直流)微电网[3].随着越来越多的新能源发电设备、储能系统和直流负载的使用,直流微电网的优势正在不断凸显[4].直流微电网中,风力发电、太阳能发电等分布式电源与储能装置配合,通过电力电子变换器给本地负荷供电,构成了分布式发电单元(distributed generation unit,DGU),多个分布式发电单元构成微电网(microgrid,MG),成为主动配电网的重要组成部分,可实现能量来源和消耗的本地化,是风能、太阳能就地消纳和高效利用的有效方式.直流MG的规模一般比较小,负荷波动及外部干扰比较频繁[5],使直流微电网的电压调节、多源协调控制及多运行模式切换等面临严峻挑战.本文主要研究直流微电网母线电压控制问题[6-7].

随着直流微电网规模的不断扩大以及不同负载的接入,直流微电网的结构以及参数存在不确定变化[8],使直流微电网母线电压存在多种波动[9],鲁棒控制是解决不确定情况下直流微电网母线电压控制的有效手段[10].李志军等[11]以多层偏心结构-AMD体系为研究对象,将鲁棒H∞控制方法应用于实际的结构振动控制工程中.王洪礼等[12]基于轮胎参数的变化建立四轮转向不确定模型,应用鲁棒H∞控制理论,对汽车四轮转向系统进行分析.常见的描述系统参数不确定的方法有两类,一类是多胞型不确定模型,采用多个顶点表示的凸集描述,如Olalla等[13]采用多胞不确定模型,研究了非线性DC-DC变换器的建模和鲁棒控制器的综合.另一类是范数有界不确定模型[14-15],需要确定不确定参数的界[16-17].石宗英等[18]采用范数有界不确定模型,研究了参数不确定机器人分散鲁棒跟踪控制;张志勇等[19]研究了参数不确定情况下车辆座椅悬架H∞输出反馈控制;陈宇等[20]研究了关联大系统的分散鲁棒H∞控制;李艳芬等[21]研究了数值界不确定关联大系统Plug-and-play分散鲁棒模型预测控制.

本文将范数有界不确定模型和小信号模型相结合,建立分布式发电单元和直流微电网的范数有界不确定模型,构建Lyapunov函数,分析系统稳定性,并由此推导以LMI表示的H∞控制器求解条件,通过求解基于LMI的鲁棒H∞优化问题,得到状态反馈控制器.利用Matlab数值仿真,分析微电网结构变化、连接线路参数和负载参数变化情况下,直流母线电压的特性,验证了该控制方法的可行性.

1 直流微电网系统的结构及模型

1.1 直流微电网系统的结构

图1为直流微电网系统的示意图[22].其中,以光伏和燃料电池为代表的分布式直流电源通过DC/DC变换器将电能输送到直流母线上,以风力机为代表的交流电源通过AC/DC变换器与直流母线相连,直流负载和交流负载分别通过DC/DC变换器和DC/AC变换器与母线连接.此外,直流母线还可通过双向DC/AC变换器与交流大电网进行能量交换,电动汽车也可通过DC/AC变换器实现高效充电.本文以最常用的分布式电源经过Buck变换器接入直流母线为例,研究直流微电网的控制问题.

1.2 直流微电网的模型

为了便于研究,本文首先对两个分布式发电单元DGUi和DGUj互联的直流微电网进行建模分析,然后将该模型扩展到由N个DGUs互联构成的直流微电网中.

图2为DC/DC变换器构成的DGUi和DGUj互联结构原理图.直流电压源表示带储能环节的分布式电源,它通过Buck变换器与公共耦合点(point of common coupling,PCC)相连接.Rij、Lij分别为互联线路电阻和电感,vi和vj为耦合点电压,vin,i和vin,j为直流电压源电压,iij为互联线路电流.负载为电阻性负载,负载电流用iL表示,DGUi和DGUj的等效负载电流分别为iLi、iLj.图3为Buck变换器的平均模型,iti和itj为Buck变换器的等效输出电流.

图2 DGUi和DGUj互联的结构原理图

图3 DC/DC变换器的平均模型

根据图2和图3,利用基尔霍夫电压定律(KVL)和基尔霍夫电流定律(KCL)得到方程:

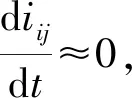
(4)

DGUj的描述与式(4)类似.在式(4)中,di和dj为变换器的占空比.从而得到QSL近似后DGUi的状态空间描述如下:

(5)

其中:xi(t)=[vi,iti]T为状态变量;wi(t)为外部扰动向量;ui(t)=divin,i为DGUi的控制输入;yi(t)为输出变量,由于Ci为单位矩阵,则yi(t)=xi(t);ξi(t)=Aijxj(t)是DGUi和DGUj之间的耦合项.系数矩阵如下:

以上是两个DGUs互联时状态方程的建立,通过上述分析,可推广到N个DGUs互联,因此N个DGUs互联时的状态空间描述为

(6)

其中:x=(x1,…,xN)T∈R2N×1为状态向量;u=(u1,…,uN)T∈RN×1为控制输入;输出变量为y=(y1,…,yN)T∈R2N×1.则系数矩阵为

2 鲁棒H∞控制算法描述

2.1 问题描述及引理

直流微电网可以看成由N个分布式发电单元子系统组成的关联大系统∑,其第i个子系统,即DGUi的状态方程为

(7)

其中:xi(t)、ui(t)、wi(t)和yi(t)分别是第i个子系统的状态变量、控制输入、扰动输入和控制输出;Aij为第i个子系统与第j个子系统的关联矩阵;ΔAii、ΔBi和ΔAij为系统参数的不确定项,假设其范数有界,则具有以下形式:

(8)

Hi、E1、E2、Gi和Nj是适当维数的常数矩阵,它们反映了不确定性的结构;Fi(t)是有界的Lebesgue可测的实矩阵函数,且满足以下条件的矩阵:

(9)

由式(7)可知,本文研究的参数具有数值界摄动的关联大系统可描述为

(10)

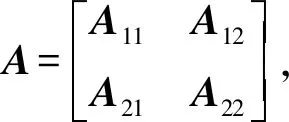
(1)A<0;

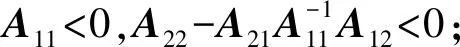
引理2[24]设D、F、E为适当维数的矩阵,存在任意的标量ε>0,则对任意满足FTF≤I的适当维数矩阵F,有DFE+(DFE)T≤ε-1DDT+εETE.

引理3[24]设X、Y、Z为适当维数的矩阵,则对任意α>0,β>0,有

2.2 标准鲁棒H∞控制系统模型

标准H∞控制问题的框图如图4所示,为保证不确定系统(7)的稳定性,将参数不确定问题转化为标准鲁棒H∞控制问题,设计目标为求解状态反馈控制器K,使得扰动输入w到控制输出y的传递函数Gyw的无穷范数上界最小,即‖Gyw(s)‖∞<γ.

图4 标准H∞控制框图

2.3 直流微电网鲁棒H∞控制器设计

本节研究直流微电网中第i个子系统 (7)的H∞控制器设计方法.假设子系统的状态可测,则为每个子系统设计一个局部状态反馈控制律:

ui(t)=Kixi(t) (i=1,2,…,N)

(11)

结合式(7)和式(11),可以得到如下闭环系统:

(12)

(13)

其中:K=block_diag{K1,…,Ki,…,KN}∈Φ,Φ为能在子系统水平上给出局部状态反馈控制的块对角矩阵的集合.数值界不确定线性大系统的鲁棒H∞控制问题,即为寻找状态反馈控制律u(t)=Kx(t),使得闭环大系统(13)渐近稳定.

基于系统(13)给出以下定义:

定义1对于任意给定的常数γ>0,若系统式(13)具有以下性质:

1) 当外部扰动输入w(t)=0时,闭环系统是渐近稳定的.

2) 在零初始条件x(t)=0下,对于所有非零的w(t)∈L2[0,∞),系统满足:

‖y(t)‖2<γ‖w(t)‖2

则称闭环大系统具有鲁棒H∞性能γ.

定理1对于由式(7)组成的大系统(10),若存在常数αi>0和矩阵Xi、Yi,使得如下不等式

(14)

成立,则由系统(12)组成的关联大系统(13)渐近稳定,且满足给定的H∞性能指标γ,其中:

R2=(E1Xi+E2Yi)T

(15)

其中:Pi为正定对称矩阵,P=diagPi.

V(x(t))关于时间t的导数为

(16)

由式(8,9)和引理2得:

(17)

由引理3得:

将式(17～19)代入式(16)得:

(20)

其中:

(21)

则wi(t)=0时:

(22)

下面证明闭环系统(13)满足鲁棒H∞性能.对给定的常数γ>0,在零初始条件下,引入性能指标:

(23)

当wi(t)≠0时:

(24)

式(24)成立的一个充分条件为

(25)

由式(25)得:

(26)

将式(26)展开为

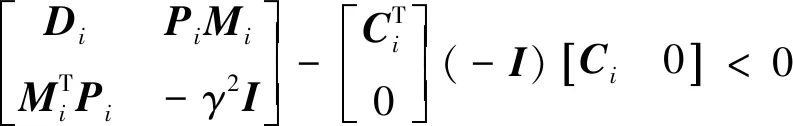
(27)

根据引理1可得:

(28)

令

(29)

根据引理1,式(29)等价于

(30)

令

则

以此类推,根据引理1,可得:

<0

(31)

对式(31)两边分别左乘和右乘矩阵diag{P-1,I,I,I,I},得:

(32)

从而定理1得证.则鲁棒H∞状态反馈控制器的设计问题,可以转化为以下最优化问题:

(33)

3 数值分析

本节针对系统(10),通过数值仿真验证控制器的有效性,主要讨论以下3点:

1) 负荷RL和线路参数Rij的变化对直流微电网性能的影响.

2) DGU的投入和退出对直流微电网性能的影响.

3) 外部扰动对直流微电网性能的影响.直流微电网系统参数如表1和表2所列.

表1 DGU互联模型参数

3.1 两个分布式发电单元互联情况下节点电压的动态特性

变换器的输出电容Cti=2.2 mF,电感Lti=1.8 mH,连接线路的电阻R12=0.05 Ω,电感L12=1.8 μH,每个DGU的负载RL=46 Ω,直流微电网的母线电压额定值48 V.

首先让DGU1和DGU2各自独立运行,相互之间不存在互联耦合.通过Matlab仿真,得到开环系统特征值为λ1,2=-55.56±j499.44.由于DGU1和DGU2模型参数一致, DGU1和DGU2具有相同的两个特征值,且都位于左半平面,DGU1、DGU2间无互联时各自稳定运行.

两个DGU互联,DGU1和DGU2互联构成的关联大系统的描述为式(10),其中:

DGU1和DGU2互联,在开环情况下,特征值为λ1,2=-55.4±j460 9.7,λ3,4=-4 600.9±j1 046.2.DGU1和DGU2互联,在上述H∞闭环控制下,特征值为λ1,2=-55.5±j4 498.1,λ3,4=-4 601.0±j276.5,说明在DGU1和DGU2互联后,状态反馈控制器的作用下,特征值均位于左半平面,闭环系统是稳定的.

DGU1和DGU2互联情况下,耦合点的电压给定值从47.6 V突变到48 V,电压跟踪过程如图5所示.对比可以看出,鲁棒H∞控制下,电压响应在很短时间内就达到稳态值48 V,能够兼顾快速性和准确性.

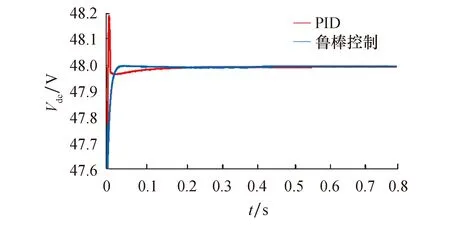
图5 DGU1和DGU2互联时的输出电压

1) 情形1.考虑DGU1负荷RL的变化,在t=0.9 s时RL由46 Ω突变到23 Ω.如图6所示,绿色代表鲁棒控制下DGU1的输出电压,红色代表PID控制下DGU1的输出电压.从图中可以看出,PID控制下,电压波动幅值较大,而鲁棒H∞控制下,电压的波动幅值较小.同时,PID控制系统中,控制器的参数选取比较复杂,需要多次调试;而基于LMI的鲁棒控制方法,能够直接求解控制器参数,简便精确.

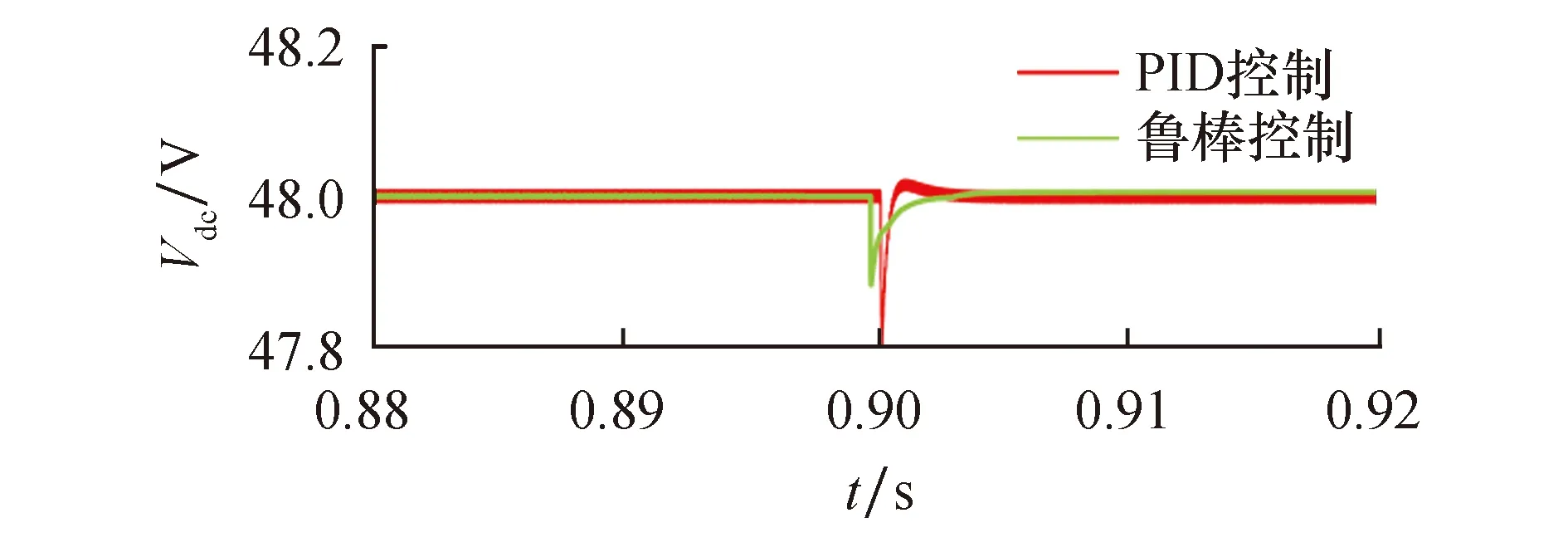
图6 RL变化时DGU1的输出电压响应

2) 情形2.考虑DGU1和DGU2之间互联线路参数变化的情况.在t=0.9 s时线路参数Rij由0.05 Ω突变到0.02 Ω.图7所示为直流母线电压的响应特性,可以看出,与PID控制相比,鲁棒H∞控制下直流母线电压波动幅值较小,恢复时间更短.

图7 线路参数Rij变化时的电压响应

3.2 DGUs投入和退出情况下节点电压的动态特性

当多个DGU互联构成微电网后,DGU之间存在互联耦合,且随着互联DGU数量的增多,耦合也增多,微电网中母线电压的调节更加复杂.

首先考虑由5个DGU互联组成的直流微电网系统,其拓扑结构如图8所示.在t=0.4 s时,DGU6投入,与DGU1和DGU5互联,互联后的直流微电网拓扑结构如图9所示.

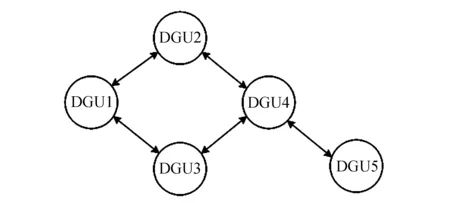
图8 多个DGU互联的直流微电网拓扑图

图9 DGU6投入后直流微电网拓扑图

图10为鲁棒H∞控制下,DGU6投入过程中,DGU1和DGU5的输出电压.从图中可以看出,DGU6在投入过程中,与其有耦合关系的DGU1和DGU5的输出电压波动小于0.3 V,电压波动小,调节时间快.

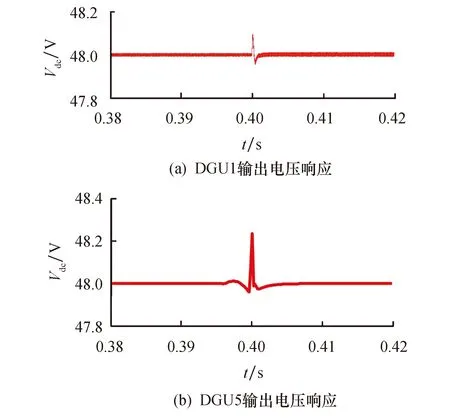
图10 鲁棒H∞控制下DGU6投入过程的电压特性

其次,在图9拓扑图的基础上,当t=0.8 s时,DGU3退出运行,即DGU3与DGU1和DGU4的连接断开.在DGU3退出过程中,与其有耦合关系的DGU1和DGU4的输出电压变化如图11所示.从图中可以看出,DGU1和DGU4的输出电压波动小于0.2 V,电压波动小,调节时间快.

从上述DGUs投入和退出情况下,电压的特性可以看出,当直流微电网中DGU的投入或退出,引起系统结构发生变化时,电压会出现波动,但在鲁棒H∞控制下,电压波动在允许的范围内,并渐近趋于稳态值.

4 结论

本文针对参数不确定情况下的直流微电网,采用小信号模型描述系统,根据Lyapunov稳定性原理,得到了一个LMI形式的控制器存在的充分条件,据此设计基于LMI的微电网鲁棒控制器.通过数值仿真验证了鲁棒H∞控制器存在可行解,可以有效地抑制不确定参数对直流微电网的影响并保证直流母线电压稳定.