基于直觉模糊三支决策的地质环境承载力评价
武 进, 粟红玉
(内江师范学院 数学与信息科学学院, 四川 内江 641100)
0 引言
地质环境承载力是衡量地质环境系统所能承受人类活动程度的重要指标,也是研究社会环境系统与地质环境系统协调发展的重要组成部分.开展区域地质环境承载力评价对区域内改善生态环境、保护生态环境、促进区域可持续发展具有重要的现实意义[1].进行地质环境承载力评价的关键步骤包括建立评价指标体系、确定权重及选取评价模型[2].因地质环境承载力影响因素具有复杂性、模糊性和不确定性的特点,目前常用的评价模型是模糊评价法[3].由于直觉模糊集(IFS)[4]能更加细腻地刻画具有模糊性的客观事物,袁名康[5]将直觉模糊TOPSIS方法引入到地质环境承载力评价中.考虑到评价者具有参照依赖和损失规避行为,本文将三支决策理论(TWD)与IFS相结合,构造基于IFS的三支决策模型[6-7],并用于解决地质环境承载力评价中的等级分区问题.
Yao[8]指出,粗糙集的三个区域(正域、负域和边界域)分别对应三种决策行为,即接受、拒绝和不承诺.TWD关键在于由损失函数和条件概率建立起三个决策规则.文献[6]主要研究了在已知的决策损失下条件概率的计算,文献[7]的条件概率是基于决策属性值的2/3原则分类得到,从而两者的分类规则都具有一定的主观性.根据各属性下各对象的直觉模糊评价信息表,本文借鉴文献[9]的方法得到各对象的相对损失函数,再利用灰色关联分析方法得到各对象的条件概率,由此建立起较为客观的决策规则.
1 基础知识
1.1 IFS及运算
一个有限论域U上的IFS[4]定义为T={x,μT(x),νT(x)|x∈U},其中,μT(x)∈[0,1]是隶属度,νT(x)∈[0,1]是非隶属度,并且0≤μT(x)+νT(x)≤1,πT(x)=1-μT(x)-νT(x)为犹豫度.通常,一个直觉模糊数(IFN)可表示为α=(μ,ν),0≤μ≤1,0≤ν≤1,0≤μ+ν≤1.
假设α1=(μ1,ν1)和α2=(μ2,ν2)是两个IFN,k>0,则α1和α2之间的运算法则规定为[4]:
①α1⊕α2=(μ1+μ2-μ1μ2,ν1ν2);
②α1⊗α2=(μ1μ2,ν1+ν2-ν1ν2);
α1和α2之间的欧式距离定义为[10]:
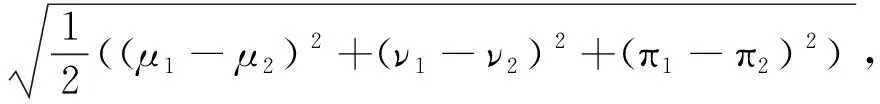
(1)
其中,π1=1-μ1-ν1和π2=1-μ2-ν2分别是α1=(μ1,ν1)和α2=(μ2,ν2)的犹豫度.
假设αi=(μi,νi)(i=1,…,n)是n个IFN,对应的权重为
则直觉模糊权重集结算子(IFWA)表示为[11]:
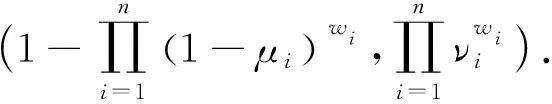
(2)
1.2 三支决策

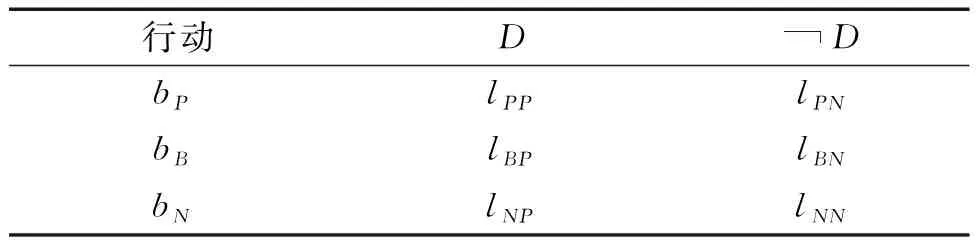
表1 损失函数[8]
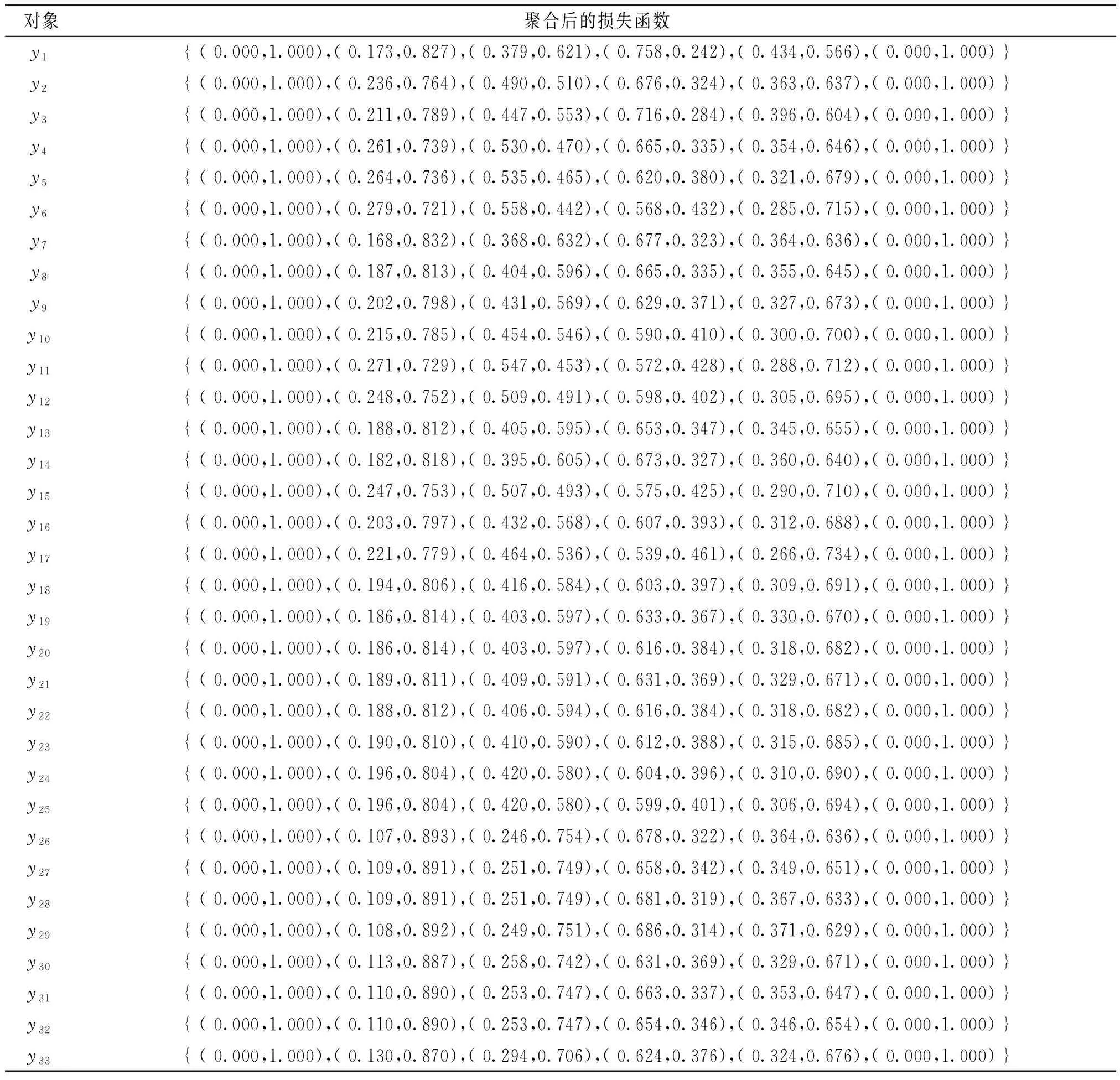
其中lPP,lBP和lNP分别表示当y属于D时,采取行动bP,bB和bN所对应的损失值;lPN,lBN和lNN分别表示当y不属于D时,采取行动bP,bB和bN所对应的损失值.通常损失函数满足0≤lPP≤lBP 若对于∀yi(i=1,2,…,m)采取行动b◆(◆=P,B,N)的预期损失如下: (3) (4) (5) 本文考虑到决策者具有参照依赖和损失规避行为,并试图改变传统“非此即彼”的方案决策模式,提出直觉模糊信息下的三支多属性决策模型,可将评价对象进行分类并排序.其中关键点在于各对象的损失函数和条件概率的确定. 假设在多属性决策(MADM)中,各评价对象y1,y2,…,ym在各属性c1,c2,…,cn下的评价信息值以直觉模糊数的形式给出,X=(χij)m×n=(μχij,νχij)m×n是评价矩阵,yi在每个属性cj下基于IFS的相对损失函数如表2所示,其中参数ρ(ρ∈[0,1])是风险规避系数,可通过实验调试得到[12]. 表2 基于IFS的相对损失函数[9] 结合表2,利用公式(2),可以得到yi基于IFS的预期损失为[9]: (6) (7) (8) 其中,Pr是Pr(D∣[yi])的缩写. 本文认为每个评价对象通常具有不同的条件概率.灰色关联度[13]的优点是分析数据序列的趋势差异,它是曲线形状之间相似性的一个很好的度量.曲线形状越接近,对应数据系列之间的关联度越大,备选方案与理想备选方案之间的灰色关联度越高,从而备选方案更接近理想备选方案.在本节中,用灰色关联度方法来计算条件概率[14].具体计算步骤如下: Step1确定直觉模糊正理想状态(IFPIS)和直觉模糊负理想状态(IFNIS). 和 其中, 0<ξ<1是识别系数,通常令ξ=0.5. Step4计算yi的灰色相对接近度: 因此,可以用RCi表示对象yi属于状态D的概率,换句话说,对象yi的条件概率是 Pr(D|[yi])=RCi. 根据贝叶斯决策过程的原理可知,最佳的决策规则应该是使成本最小的决策规则[15].Liu等[9]基于IFS给出了三种不同的决策规则,即积极观点、消极观点和综合观点.本文使用综合观点的决策规则,即: (P)如果I(R(bP∣[yi]))≤I(R(bB∣[yi]))和I(R(bP∣[yi]))≤I(R(bN∣[yi])),则yi∈POS(D); (B)如果I(R(bB∣[yi]))≤I(R(bP∣[yi]))和I(R(bB∣[yi]))≤I(R(bN∣[yi])),则yi∈BND(D); (N)如果I(R(bN∣[yi]))≤I(R(bP∣[yi]))和I(R(bN∣[yi]))≤I(R(bB∣[yi])),则yi∈NEG(D). 其中I(R(b◆∣[yi]))(◆=P,B,N)是预期损失的理想正值,其计算公式如下: (9) (10) (11) 已知X=(χij)m×n=(μχij,νχij)m×n是评价矩阵,属性的权重向量为ω1,ω2,…,ωn,则评价对象的分类和排序过程如下: Step 1根据2.1节得到每个对象yi在每个属性cj下的相对损失函数,表示为: Step 2利用公式(2)获得yi在所有属性下相对损失函数的聚合值,即: (12) Step 3使用2.2节中提出的方法,计算yi的条件概率Pr(D|[yi]). Step 4根据2.3节中的决策规则(P)-(N),确定yi所属的域:POS(D)、BND(D)或NEG(D),得到分类结果. Step 5对所有对象进行排序.排序规则为:①POS(D)中的对象最优先,BND(D)的居中,NEG(D)的最后;②同一个域中的对象根据R(yi)的值进行排序,R(yi)值越小,yi越优先.R(yi)的计算公式为: (13) 本节将所提方法应用于地质环境承载力评估的实例中验证其可行性,并通过另一个分类排序实例说明排序规则的有效性. 以文献[5]的实例为例,来说明本文提出的基 于IFS的三支决策方法在地质环境承载力评估过程中的应用.将某市划分出33个地形地貌单元,并以此作为该市地质环境承载力评估的研究对象.根据地质环境调查数据,该市地质环境承载力的评价体系主要由地形起伏度(最高点海拔高度与最低点海拔高度的差值)、地形地貌(陆地表面形态特征的归类)、工程地质岩组(地质岩性特征,岩组越坚硬,地质灾害越容易发生)、活动断裂距离(距离活动断裂的距离越近,地质灾害易发程度越高)、岩溶发育程度、年平均降雨量、土地利用程度、地震动峰值加速度这8个属性的数据组成.根据专家打分法得到属性的权重向量为W={0.10,0.10,0.17,0.17,0.10,0.17,0.08,0.11}.该市地质环境承载力评价矩阵X=(χij)m×n=(μχij,νχij)m×n见文献[5]中的直觉模糊决策矩阵. 第一步,假设ρ=0.4,由公式(12)可得33个对象按属性进行聚合后的相对损失函数值(见表3). 表3 聚合后的相对损失函数值 第二步,计算得到33个对象的条件概率分别为: Pr=(0.509,0.555,0.535,0.567,0.573, 0.592,0.514,0.524,0.541,0.558,0.583,0.565,0.525,0.518,0.570,0.544,0.569,0.540,0.531,0.534,0.531,0.535,0.537,0.540,0.541,0.488,0.494,0.485,0.484,0.502,0.490,0.493,0.511) 第三步,根据公式(9)—(11),可以得到相对损失的理想正值(见表4). 第四步,根据2.3节中的决策规则(P)-(N),确定每个对象所属的域为:POS(D)={y4,y5,y6,y11},BND(D)={y2,y3,y9,y10,y12,y15,y16,y17,y18,y23,y24,y25},NEG(D)={y1,y7,y8,y13,y14,y19,y20,y21,y22,y26,y27,y28,y29,y30,y31,y32,y33}. 第五步,根据公式(13)和排序规则,排名前4的对象的排序结果为:y6>y11>y5>y4. 地质环境承载力高的这四个区域地形相对平缓,地质灾害隐患点密度小;人类工程活动强,经济建设较为发达.近几年来,地下水开采强度的限制、湿地保护、生态环境保护措施的大力执行,使得这些区域的地质环境承载力明显优于其他区域.对地质环境承载力高的区域可发展生态经济、加强生态绿地建设. 为了进一步验证模型在分类排序问题中的有效性,将此方法应用于解决文献[16]的示例.假设ρ=0.4,结果如表5所示.从表5可以看出,本文提出的方法不仅可用于评价对象的分类,也适用于评价对象的排序,并且排序结果与文献[16]基本一致,获得的最佳对象均为y1. 表5 同已知方法的比较结果 本文研究了基于直觉模糊的三支决策模型中相对损失函数和条件概率的确定问题,并建立了相应的决策规则,较好地实现了对评价对象的分类和排序,还将该方法应用于地质环境承载力评估的研究中.进一步的研究方向主要包括:(1)大数据时代,越来越多的决策者可以通过网络参与决策.如何更准确地用各种模糊集表达决策者的评价信息是一个非常重要的研究课题.该方法可以扩展到更多类型的模糊集,例如犹豫模糊集、区间模糊集和毕达哥拉斯模糊集等[17].(2)近年来,泥石流、地震等自然灾害频发.如何快速、合理地预测突发事件后的应急救援物资需求,是应急救援的核心.该方法也可用于解决应急物资需求安排问题.



2 基于IFS的三支决策模型
2.1 基于IFS的相对损失函数
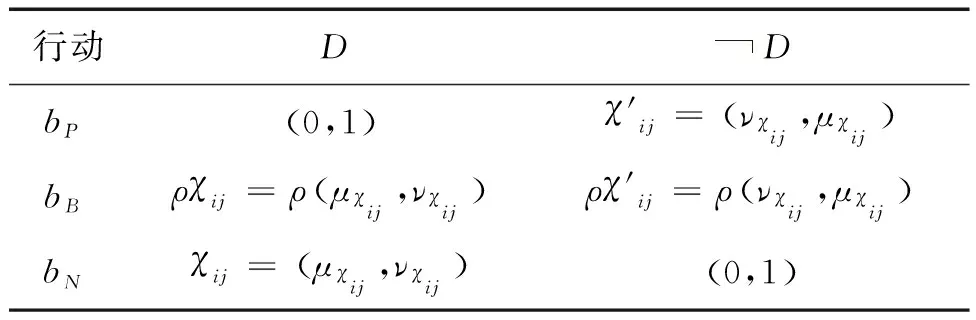
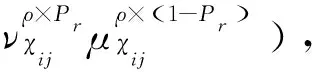
2.2 基于灰色关联度的条件概率

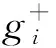
2.3 决策规则
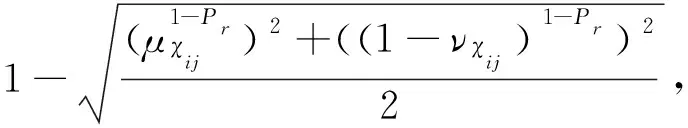

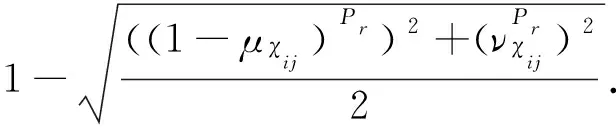
2.4 模型的决策过程
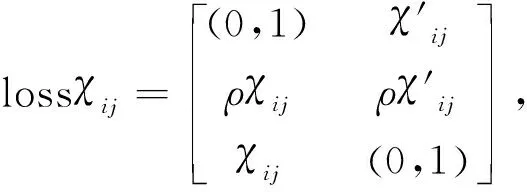
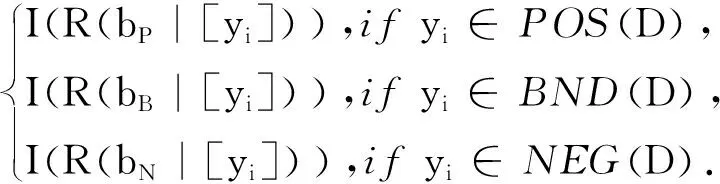
3 结果与分析
3.1 地质环境承载力评估实例
3.2 对比分析

4 结束语

