谈高考真题的新解、剖析与逆向设计的尝试——以2023年高考两道解析几何试题为例

骆银海

(诸暨市教育研究中心,浙江 诸暨 311899)

高考真题凝聚了命题专家的心血与智慧,又广泛吸收了中学基础教育研究的最新成果,是引导中学教师教学方向的标杆．因此,要围绕高考真题进行解法创新、试题形成机理剖析是常见的解题教学模式,但仅围绕高考真题思考是远远不够的,还要对高考真题的前因后果进行溯源拓展.教师可通过逆向设计,判断从结论到条件的命题是否成立,充分应用好这一宝贵的教学资源.这一探索的过程恰好是得到创新解法的过程,有些解题方法无论在理论上还是在实践上都是全面的创新．基于此,本文以2023年两道高考解析几何试题为例,谈高考真题的新解、剖析与逆向设计的尝试．

1)求p的值;

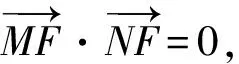
(2023年全国数学高考甲卷理科试题第20题)

由题目所给条件,不难得到p=2,同时记抛物线为C:y2=4x,下面重点介绍第2)小题的分析步骤与解法．

2)解法1 先画出草图(如图1),延长MN交x轴于点T.设直线MN的方程为x=my+t,点M(x1,y1),N(x2,y2),T(t,0),联立方程组

图1

得

y2-4my-4t=0,

判别式Δ=16(m2+t),由根与系数的关系,得

y1+y2=4m,y1y2=-4t.

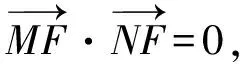
=(my1+t-1)(my2+t-1)+y1y2

=(m2+1)y1y2+(mt-m)(y1+y2)+(t-1)2

=-4t(m2+1)+4m2(t-1)+(t-1)2=0.

从而

4m2=t2-6t+1≥0,

解得

此时,判别式

Δ=4(4m2+4t)=4(t-1)2,

从而

于是

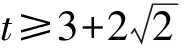
又

计算线段MN的长度和点F到直线MN的距离d分别为

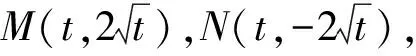
解法2 如图2,作FQ平行y轴交MN于点Q,设直线MN的方程为y=kx+n,联立方程组

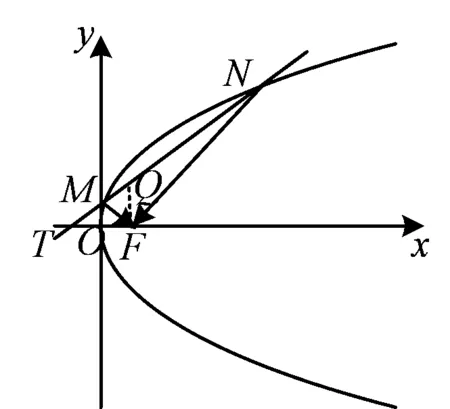
图2

可得

k2x2+2(nk-2)x+n2=0,

其根的判别式

Δ=16(1-nk),

由根与系数的关系,得

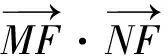
=(1+k2)x1x2+(nk-1)(x1+x2)+n2+1=0,

于是

(n+k)2=4(1-nk),

故

n2+6nk+k2-4=0,

整理得

解得

又

于是

也可以利用抛物线焦半径公式结合三角函数来求|FM|和|FN|的值,其解答过程如下:

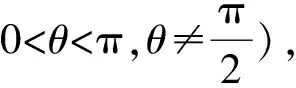
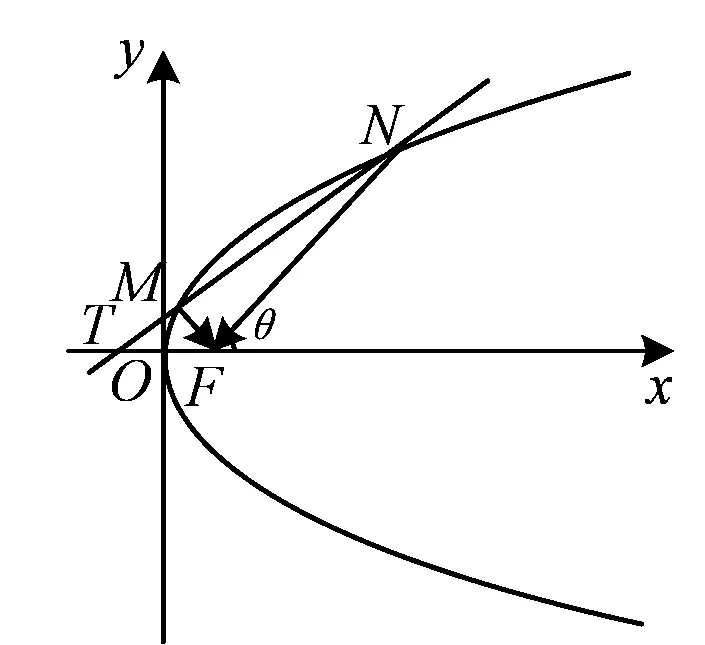
图3

|FN|=1+xN=2+|FN|cosθ,

故

同理可得

因为

评注 处理最值的方法还可以通过换元,应用二次函数进行配方．

图4

1)试用两种方法求△POQ面积的最大值,比较这两种解法的简洁性;

2)设点R(3,-1),用割补法求RQEP的面积S(k)的表达式．

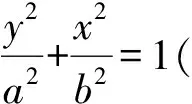
1)求曲线C的方程.

2)过点(-2,3)的直线交曲线C于点P,Q,直线AP,AQ与y轴分别交于点M,N．求证:MN的中点为定点．

(2023年全国数学高考乙卷理科试题第20题)

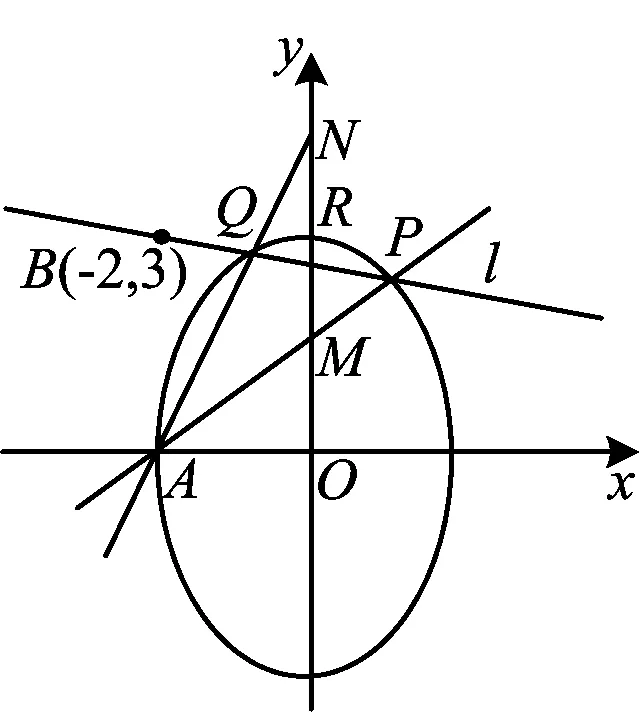
图5

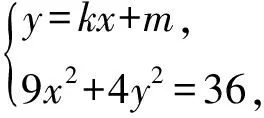
(4k2+9)x2+8mkx+4m2-36=0.

由根与系数的关系,且3=-2k+m,得

易得直线AP的方程为

令x=0,得

同理可得

设MN的中点R(0,y0),则

即

=2k+(3-2k)=3,

故线段MN的中点为定点R(0,3)．

逆向设计 现在不再探讨真题的其他解法了,而是把条件与结论换过来,设MN过定点R(0,3),反向推导直线PQ(记为l)过定点,其他条件都不变．

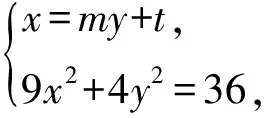
(9m2+4)y2+18mty+9(t2-4)=0.

由根与系数的关系,得

从而

2mty1y2+(t2-4)(y1+y2)=0.

易得直线AP的方程为

令x=0,得

同理可得

因为R(0,3)是MN的中点,所以

整理得

(3m2-2m)y1y2+(t+2)(3m-1)(y1+y2)+3(t+2)2=0,

把根与系数的关系代入,得

(t+2)(3m+t+2)=0.

又因为t≠-2,所以

t=-3m-2,

因此,直线l的方程为

(y-3)m-(x+2)=0.

由于m可取无数个值,则

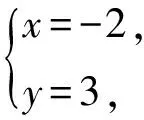
解法2 设M(0,3-t),N(0,3+t),其中t是任意正数,设P(x1,y1),Q(x2,y2),则直线AM为

即

2y=(3-t)(x+2).

(t2-6t+18)x2+4(3-t)2x+4t2-24t=0.

由根与系数的关系,得

从而

则

用-t替代t,可得

于是

进而直线PQ的方程为

化简可得

故直线l过定点(-2,3)．

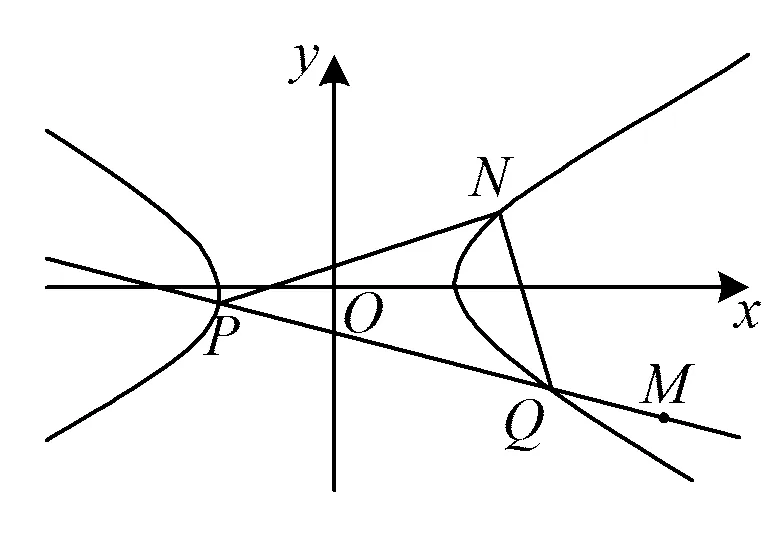
图6

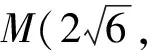
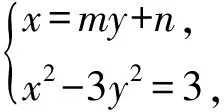
(m2-3)y2+2mny+n2-3=0.

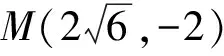
从而

记N(x,y),则

观察这个算式,计算结果是什么?

发现是二元二次三项式,二次项为(m2+1)y1y2,一次项为(mn-mx-y)(y1+y2),常数项为(n-x)2+y2,即

(m2+1)y1y2+(mn-mx-y)(y1+y2)+(n-x)2+y2=0.

(1)

接下来该怎样思考呢?下面是一些学生提出的想法．

关于m的二次方程(1)有实数解,判别式Δ≥0,再配方成非负数和小于等于0,即配方成形如

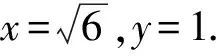
教师提出疑问 能完成如此复杂的运算吗?即使能辛苦完成运算,请思考一下,方程(1)中有几个实数解?与实际情况吻合吗?

教师启发学生思考,让问题回到数学的本质.方程(1)不能看成关于m的狭隘的二次方程,而是关于任意实数m都成立的恒等式,也就是说m至少有3个以上的解．因此,

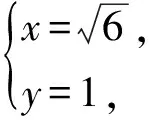
解后反思 涉及关于实数x的一元二次方程,学生长期仅对狭隘的一元二次方程ax2+bx+c=0(其中a≠0,a,b,c∈R)研究得比较透彻,但对于广义一元二次方程ax2+bx+c=0(其中a,b,c∈R)的研究完全处于零状态.广义一元二次方程可能存在有3个以上的多解情形,其条件是a=b=c=0．事实上,关于x的广义一元一次方程在解析几何中的应用也远远不够,如果在解题中有意识地使用会起到四两拨千斤的作用.

图7

(4k2-3)x2+24kx+24=0.

由根与系数的关系,得

即

-kx1x2=x1+x2.

直线PQ1的方程为

(2)

直线QP1的方程为

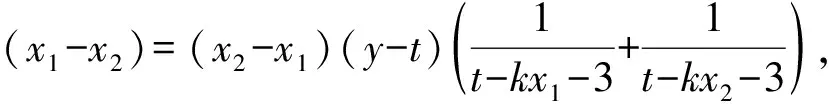
化简得

即

(2ty-3-t2)(4k2-3)+18(y-2)=0.

由于k是任意实数,则4k2-3有无数个解,由广义一元一次方程有无数解的条件得

故直线PQ1和直线QP1相交于定点H(0,2),t=1.

结束语 高中数学教学的重要类型之一是解题教学.以高考真题为载体进行复习课教学需要解决“使用什么教学方法?推介什么创新解法?渗透什么数学思想?养成什么思维品质?怎样拓展试题?”等问题,这样才能形成发展性的教学效果.创新解法,剖析试题形成机理,并进行试题逆向设计就能很好地处理上述问题,起到举一反三的作用,促进教学深层次的发展．