基于几何直观的“单元—课时”教学设计——以“函数”单元中的“一次函数的图象”为例

傅瑞琦

(金华市教育教学研究中心,浙江 金华 321000)

为实现核心素养导向的教学目标,整体把握教学内容之间的关联,帮助学生建立能体现数学学科本质、对未来学习有支撑意义的结构化的数学知识体系[1],要改变过于注重以课时为单位的教学设计,推进单元整体教学.“单元—课时”教学设计是在单元教学设计的基础上,给出课时教学设计,以充分体现教学的整体性、逻辑的连贯性、思想的一致性、方法的普适性和思维的系统性[2],体现数学知识之间的内在逻辑关系,以及学习内容与核心素养表现的关联.

“一次函数”是浙教版《义务教育教科书·数学》(以下统称“教材”)(八年级上册)第五章的内容,是学生学习函数概念后学习的第一个特殊函数.画出函数图象这一数形结合活动,是认识函数概念、发现函数性质、理解函数本质的重要环节.如何通过画函数图象从整体与结构上认识函数要素之间的关联,从而培养几何直观?笔者以“一次函数的图象”为中心课时,探讨基于几何直观的“单元—课时”的教学设计,引导学生感悟数学思想方法,理解数学本质.

1 单元内容、目标及解析

函数主要研究变量之间的关系,表达现实世界事物的简单规律,是第4学段(7～9年级)“数与代数”的核心内容,对高中进一步学习函数具有“脚手架”的作用.每一类特殊函数都隶属于“函数”大单元,不同函数之间都存在一些必然的、逻辑上的联系,将它们整体看待更能体现知识内容的整体性、思想方法的一致性,为学生整体把握知识、提升素养提供了载体.

1.1 单元内容及解析

函数是学生学习“数与式”“方程与不等式”后学习的第3个主题,其单元知识结构图如图1所示,围绕函数的要素(对应关系),形成“引入变量—对应关系—画出图象—探究性质—解决问题”的学习结构,即从问题情境中抽象概括函数概念,借助在直角坐标系中的描点,理解函数图象与表达式的对应关系,直观得出性质,在应用中感悟函数本质,增强几何直观,发展应用意识.

图1

1.2 单元目标及解析

目标1 经历从问题情境中发现变量之间的数量关系获得研究对象的过程,通过“观察、分析、概括”获得函数概念,体悟相关函数概念获得的一般方法.

达标标志 通过对两个变量对应关系的分析,表述概念.

目标2 经历从函数表达式出发,通过“列表、描点、连线”探究图象的类型,会画3种函数的图象,知道它们的整体特征、变化规律,获得函数性质.

达标标志 描点画出函数图象,能通过观察、分析、归纳得出图象性质,结合图象对函数关系进行分析.

目标3 能用函数相关知识解决简单实际问题,掌握其学习路径,形成结构化的知识体系,进一步发展模型观念、抽象能力、几何直观和推理能力.

达标标志 能从实际问题中建立函数模型,利用函数有关知识解决问题,能梳理函数的学习思路,推广、类比并规划一个新函数的学习路径.

2 课时教学设计

“单元—课时”教学设计是在整体分析教学内容和学生认知规律的基础上,让学生经历前后一致、逻辑连贯的完整学习过程.在宏观层面上,笔者围绕函数的要素,让学生经历函数“画出图象—概括性质—解决问题”的学习过程;在微观层面上,关注每一环节,将之前学习函数获得的方法迁移到新函数的学习中,深化知识结构.为此,笔者选择函数图象这一单元,规划学习课时,选择“一次函数的图象”进行课时设计(见表1),重点关注几何直观的形成途径.

表1 “一次函数的图象”课时设计

2.1 课时教学目标

1)经历“取值列表、描点连线”得到一次函数图象的过程,加深对函数概念的理解,感受变化与对应的数学思想;

2)会画一次函数的图象,了解其意义,会求一次函数的图象与坐标轴的交点;

3)完善一次函数图象的学习路径,发展图象获得过程中的抽象能力,数与形关联中的几何直观,观察、归纳和论证过程中的推理能力.

2.2 教学重点和难点

重点 画一次函数的图象.

难点 学生能够从感性角度接受“一次函数的图象是一条直线”,但从理性角度接受,验证图象的完备性(在直角坐标系中满足一次函数表达式的点在直线上)、纯粹性(图象上点的坐标满足函数表达式),学生不容易理解其意义,这是本节课教学的难点.

3 教学过程设计

3.1 提出问题

问题1 在A型的弹簧下悬挂质量分别为1 kg,2 kg,3 kg,……的小球,记下弹簧长度(见表2).若小球的质量为2.5 kg,试求弹簧的长度.

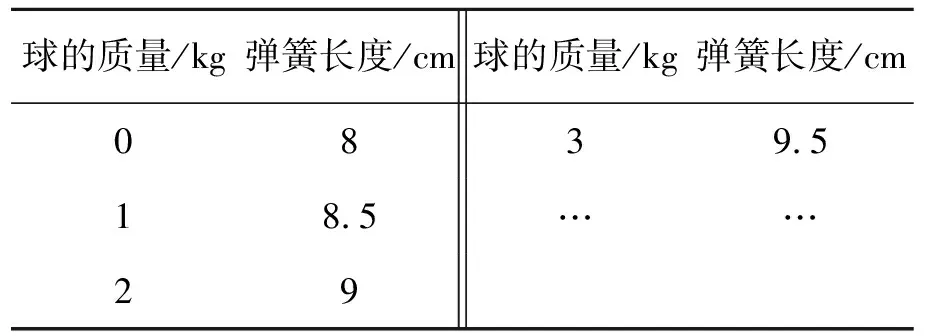
表2 弹簧长度变化

师生活动 学生归纳,小球每增加1 kg,弹簧长度增加0.5 cm.当小球的质量为2.5 kg时,弹簧的长度为9+0.5×0.5=9.25(cm).

追问1 弹簧的长度y(cm)与小球的质量x(kg)之间是函数关系吗?

师生活动 依据函数概念,关系式为y=0.5x+8,是一次函数.

追问2 如图2,若将各弹簧间隔相同距离摆放,观察有什么特征?

图2

设计意图 在实验情境中抽象出一次函数模型,直观感受一次函数图象.问题1的设问是基于图象加密活动,让学生感受点与点之间还有无数个点需要探究,体会学习函数图象的必要性,为形成推理能力和抽象能力做准备.

追问3 联系函数概念,将学习一次函数哪些内容?如何学习?

设计意图 联系图象法的直观优点、学生已有的知识结构,提出学习函数图象的必要性.围绕函数图象的组成要素(符合表达式的点),数形结合地研究函数,形成函数的学习路径.

3.2 探究图象

问题2 什么是函数图象?如何画出函数y=kx+b的图象?

师生活动 通过取值、描点和连线画出图象,采取特例研究的方法,如先画y=2x,y=2x+2等的图象来总结画图方法形成函数图象的概念.

探究1 画一次函数y=2x的图象.

思考 该函数表达式有什么特征?根据这个特征思考如何取值,并猜想图象特征.

师生活动 引导学生根据表达式的代数特征,猜想图象的几何特征.

追问1 根据表3的数据在图3中描点,描出的这些点有什么特征?如何说明坐标满足y=2x的点都在这条直线上?

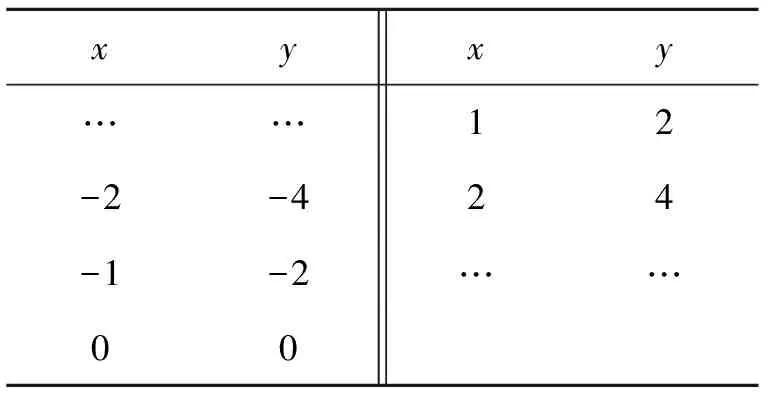
表3 以x=0为基准左右对称取值

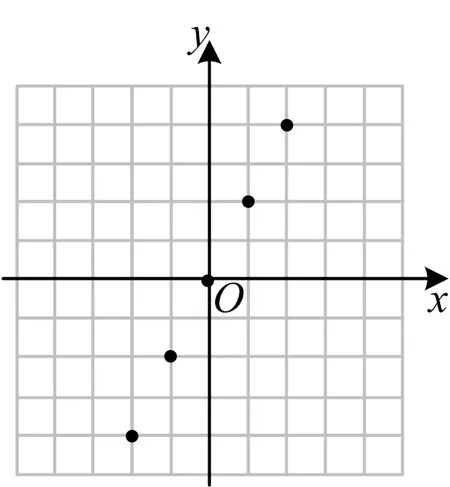
图3

1)当x=0时,y=0,图象过原点;

2)当x,y的值同正或同负时,图象过第一、第三象限;

3)当x=2时,y=4,或当x=-2时,y=-4,图象关于原点对称;

4)当x=1时,y=2,或当x=2时,y=4,函数值随着x的增大而增大;

……

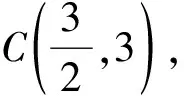
追问2y=2x的图象一定是一条直线吗?如何验证?

师生活动 经历用几何画板软件验证的过程.一是验证图象的完备性,如图4,在任意两点之间作一点M(m,2m),说明满足y=2x的点都在这条直线上;二是验证图象的纯粹性,如图5,在直线上取一点P(x,y),度量点的坐标满足y=2x,说明直线上任意一点的坐标都满足函数表达式.

图4 图5

设计意图 借助特例y=2x,获得“根据特征取值—描点—顺次联结—加密验证”的图象一般画法.借助几何画板软件进一步验证图象的完备性和纯粹性,感悟思维的严密性,发展几何直观.

探究2 画一次函数y=2x+2的图象.

思考y=2x+2与y=2x在形式上有何联系?根据这个关系如何取值?

师生活动 根据表4的取值描点后发现,相同x值的对应点,函数y=2x图象上的点都向上平移2个单位就是y=2x+2图象上的点.

表4 以x=0为基准左右对称取值

追问1 试猜想函数y=kx+b(其中k≠0)与函数y=kx的图象关系?如何简便地画一次函数y=kx+b的图象?你有什么经验?

师生活动 概括得出函数y=kx+b(其中k≠0)与y=kx的图象是互相平行的直线.根据“两点确定一条直线”,简化画函数图象的方法.

设计意图 通过列表、描点发现两个图象的平移关系,即函数y=kx+b的图象可以转化为函数y=kx的图象,优化画图过程,经历从特殊到一般,感受化归转化思想,进一步发展几何直观.

3.3 画出图象

问题3 在同一直角坐标系中画出函数y=3x,y=-3x+2的图象.

师生活动 画出图象(如图6),为方便描点,取点的坐标尽可能是整数.

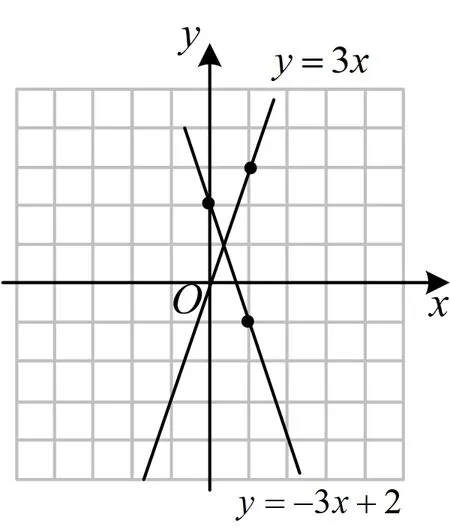
图6

追问1 试判断点(-2,-6)是否在函数图象上?

师生活动 方法1是把x=-2代入函数表达式求值,判断y值是否为-6;方法2是由y=-6,得方程-6=3x和-6=-3x+2,求得解是否为-2.

追问2 如何求图象与坐标轴的交点坐标?如何求两条直线的交点坐标?

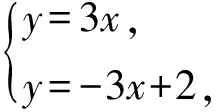
设计意图 通过判断点是否在函数图象上,以及求交点坐标,体会点的坐标与函数表达式之间的关系、方程与函数的关联,进一步体会图象的直观作用以及数形结合的思想.

追问3 说一说“一次函数表达式”“函数图象上的点”“函数图象”之间的关联.

师生活动 引导学生总结,通过“一次函数表达式”取两组对应值,描出两点画出直线(函数图象),也可以在直线(函数图象)上取两点,求该“一次函数表达式”.

设计意图 通过画图象后的解题反思,进一步领会“表达式、图象上的点、图象”之间的关联,自然引出待定系数法求函数表达式,完善研究函数的路径.

3.4 问题解决

问题4 B型弹簧不挂小球时长6 cm,挂上小球后伸长的长度与所挂的小球质量成正比,挂上1 kg的小球弹簧的长度为6.9 cm.当用相同质量的小球时,该弹簧与问题1中A型弹簧的长度能否相等?

思考 你能通过画图象的方法判断吗?

师生活动 设弹簧的长度为y(cm),小球质量为x(kg),在图7中画出两个函数的图象,两直线有交点,说明两弹簧的长度能够相等.

图7

追问1 你能求两直线的交点坐标吗?其实际意义是什么?

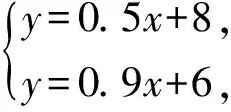
设计意图 通过画图象后进行判定,体现图象的直观性.用图象知识解决问题,再一次体现图象的意义和用处,发展几何直观和推理能力.

3.5 概括总结

问题5 通过本节课的学习,获得了哪些新知?是按照怎样的路径研究?进一步将学习什么内容?

师生活动 引导学生通过小结,概括出知识结构图.

设计意图 将本节课的知识纳入一次函数的知识结构中,指出进一步学习的内容和方向(图象性质和应用),形成完整的知识体系,进一步完善学习路径.

4 教学建议

函数的教学目标是要让学生理解用函数表达变量关系的实际意义,体会建模思想;理解函数图象与表达式的对应关系,增强几何直观;会用函数表达现实世界的变化规律,发展应用意识.

4.1 运用图表体验函数模型

图表具有信息量大、整体性强、直观明了等特点,常成为人们表达和交流的重要工具[3].因此,在一次函数的研究中,通过取值列表,一是感知变量的对应关系、函数表达式与图象的关联;二是初步感知函数的性质、系数对图象的影响等,如用点坐标的符号判断图象所经过的象限;三是发现函数y=2x与y=2x+2图象间的平移关系,即研究函数y=kx+b的图象可转化为研究函数y=kx的图象问题,体现化归思想,为其他特殊函数图象的研究提供路径,发展基于图表的几何直观.

4.2 数形结合发展推理能力

直角坐标系可以直观描述函数两个变量之间的对应关系,为数形结合提供逻辑基础,通过数形结合活动帮助学生借助图象的直观,逐步形成代数形式的直观,从而发展数学直觉.例如,y=2x的代数特征与函数图象特征的关联,为“形”的角度研究函数提供基础.求图象的交点坐标,是用函数的观点,即用图象的直观性来处理方程问题.又如,数(y=kx+b)与形(直线)的对应关系,斜率k相同的两条直线可以互相平移等,形成从几何变化的视角研究图象、探索性质的思维,将抽象的逻辑推理体现在具体的图象之中.关注基于代数的逻辑推理,基于图象的函数想象,提升发现问题、提出问题、分析问题和解决问题的能力,以及有逻辑地表达与交流的能力,促进推理能力的形成.

4.3 提炼路径实现方法迁移

本单元主要研究对象是函数,需要以一次函数的研究为起点,完善研究函数的途径、依据、结果等,构成研究方法体系,为后续学习反比例函数、二次函数提供路径.如图8,在一次函数图象的研究中,形成“一般描点法”到“方法优化”的结构,应用该结构研究反比例函数图象,并深化结构研究二次函数图象.通过类比,进行前后连贯、逻辑一致的教学,帮助学生构建有序、系统的知识结构,促进知识与方法的迁移,以及几何直观等核心素养的形成.

图8

[1] 中华人民共和国教育部.义务教育数学课程标准(2022年版)[M].北京:北京师范大学出版社,2022.

[2] 章建跃.《普通高中教科书·数学(人教A版)》“单元—课时教学设计”体例与要求[J].中学数学教学参考(上旬),2019(8):14-16.

[3] 鲍建生,章建跃.数学核心素养在初中阶段的主要表现之三:几何直观[J].中国数学教育(初中版),2022(7/8):3-9.