茶泡七分好 题品几番妙
——一道中考复习题的解题教学
陈 刊
(杭州市开元中学,浙江 杭州 310000)
好茶经久耐泡,方能品鉴其中真味;好题多番思考,方能探寻解题奥秘.笔者在执教九年级学生数学中考复习时遇到一道题,品题数番,并进行了教学实践,效果显著.现整理成文,以期为广大一线教师在解题教学方面提供借鉴.
1 试题呈现
例1 如图1,△ABC为等腰直角三角形,∠CAB=90°,在BC的延长线上取一点D,以AD为腰作等腰Rt△ADE,AC,ED的延长线相交于点G,F是线段DG上的点,且∠DCF=∠DAC.联结CE,若GF=2,EF=4,则DF=______.

图1
分析 此题来源于浙江省杭州市初中数学命题能力评审比赛的参赛题库,适合作为数学中考复习卷填空题的最后一题.此题以学生熟悉的等腰直角三角形为载体,延长斜边后慢慢展开边、角之间的特殊关系,分析角度、解决思路和涉及的知识点较多,能有效地考查学生的综合应用能力和解题思维能力.
2 学情分析
处于中考复习的学生已经学习了等腰三角形、相似三角形、切割线定理、四点共圆、勾股定理、锐角三角函数、平面直角坐标系等知识.学生已具备了几何推理能力,但综合运用能力有待加强,搭建条件与结论之间桥梁的能力急需提高.此题可以进一步加深对几何图形的认识、图形性质的转化,优化解题路径,为学生探究平面几何问题提供一般策略和一般方法.
3 教学实施
3.1 初品题目——独立思考,梳理条件
学生独立思考数分钟,梳理条件和所求结论(如图2).许多学生无法建立从条件到结论的桥梁,出现了思维卡顿.作为一道压轴题,题目所给的丰富条件足以让学生产生探究欲望.

图2
3.2 再品题目——转化条件,寻找味道
罗增儒教授提出,寻找解题思路的过程就是寻找条件知识与结论知识之间的逻辑联系或转化轨迹的过程[1].解题教学中应多鼓励学生转化条件,寻找知识间的联系.
转化1 具有公共顶点A的等腰Rt△ACB与Rt△ADE,转化成学生熟悉的基本几何模型——手拉手模型,从△ACB∽△ADE得到△DAB≌△EAC.由∠CDA=∠CEA,得∠DCE=∠DAE=90°(如图3),可得隐藏条件——点D,C,A,E共圆.

图3
转化2 ∠DCF=∠DAC的转化的确棘手.寻找图形中其他相等的角:两个等腰直角三角形的4个底角和其中∠ACB的对顶角∠DCG都相等.两组相等的角产生的火花:∠G=∠ADE-∠DAC和∠GCF=∠DCG-∠DCF.可得另一个隐藏条件:∠G=∠FCG,即等腰△GFC.
教学说明 条件与结论之间的桥梁在不断转化中慢慢形成.再品题目,品出了熟悉的味道(手拉手模型)和隐藏的味道(四点共圆、等腰三角形).
3.3 解法呈现
思路1 利用线段的转化构造子母型相似.
从线段的角度分析:在直线GF上,已知GF=2,EF=4,求EF中FD的长度.利用转化2中结论GF=CF,使得原本同一直线的两条线段转化为△FEC的两边(如图4).学生对于三角形的边角处理颇为熟悉,由线段FD,FC,FE的位置关系,不难想到“子母型相似”.

图4 图5
解法1 如图5,由点D,E,A,C共圆可知
∠DEC=∠DAC,
且
∠DAC=∠DCF,
得
∠DEC=∠DCF,
则
△FDC∽△FCE,
从而
于是
思路2 利用切割线定理求出半径.CF与圆有什么关系?相切吗?
解法2 如图6,取DE的中点O,联结OC.因为∠DCE=90°,所以OC就是点D,E,A,C共圆的半径.由解法1知∠1=∠2,又因为∠2=∠3,所以∠3=∠1,从而

图6
∠FCO=∠DCE=90°,
于是CF是⊙O的切线.由切割线定理可得
FD·FE=CF2=GF2=4,
故
FD=1.
思路3 利用勾股定理求半径.既然求得∠FCO=90°,因此△COF为直角三角形.直角三角形的三边关系有助于更好地解释图形,如求⊙O的半径.
解法3 设⊙O的半径为r,则
OF=EF-OE=4-r.
在Rt△COF中,由勾股定理得
OF2=CF2+CO2,
即
(4-r)2=4+r2,
解得r=1.5,故
FD=FE-DE=1.
思路4 渗透解析法,改“斜”归“正”.
GF与FE的长度确定了点F在线段EG中的位置.求FD即求点D在线段EG上的位置.由于GE是一条斜线,不妨将其改“斜”归“正”:如图7,过点F,D,E分别作直线AC的垂线段FM,DN和EQ,可将GE上各点的位置转化到线段GQ上.
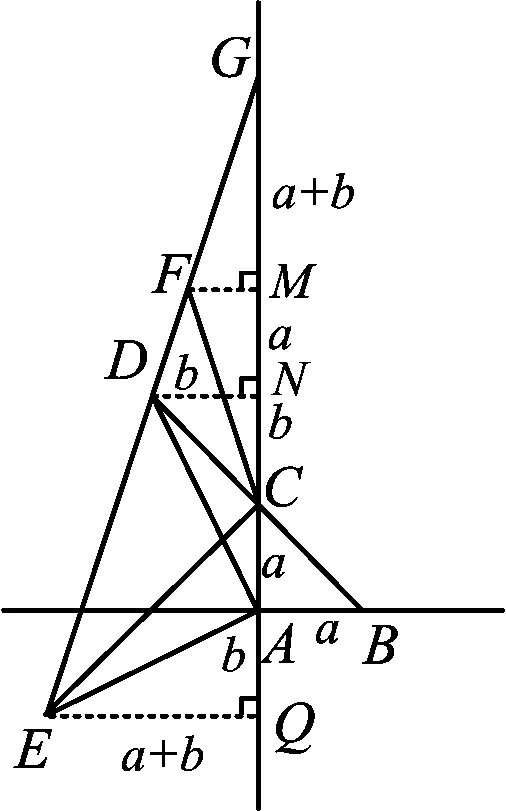
图7

解法4 如图7,过点F,D,E分别作直线AC的垂线段FM,DN和EQ.由等腰Rt△ADE易得Rt△DNA≌Rt△AQE,由∠BCA=∠NCD=45°知△DNC是等腰直角三角形.设AC=AB=a,NC=DN=b,则
EQ=NA=a+b,
且
AQ=DN=b,
从而
CQ=AC+AQ=a+b,
于是
GM=CM=CQ=a+b,
因此
MN=CM-CN=a.
因为△GDN∽△GEQ,所以
即
化简得
a=b,
则N是GQ的中点,D是GE的中点,故
DF=GD-GF=3-2=1.
教学说明 解析法虽略显烦琐,但其体现了几何图形代数化.数形结合将图形性质化为代数式处理,具有普遍意义,这也是学生高中阶段学习几何的重要思想方法之一.
3.4 三品题目——关注图形刻画,再探解法
熟悉的味道,不一样的配方.细品点D在斜边BC的延长线上,即点D决定了△ADE的大小.两条直角边AC与AD之比为手拉手模型中两个等腰直角△ACB与△ADE的相似比,同时AC,AD恰好构成∠DAC.细品题目,关注基本图形的刻画.
思路5 巧用正切值刻画角.
如何刻画一个角,除了能求出角度,还可以用锐角三角函数刻画.
如∠DAC,过点D作DM⊥AC于点M(如图8).用两个等腰直角三角形相似比可以刻画∠DAC的正切值,但求不出确定值.
又如∠DCF,过点D作DH⊥CF于点H(如图9),构造Rt△DCH后同样难以刻画角度.突破口在哪里?还有相等的角吗?
解法5 如图5,由点D,E,A,C共圆可知∠DEC=∠DAC.由∠DCE=90°,得
由△FDC∽△FCE且CF=GF,得
即
在图8中,∠BCA=∠MCD=45°,得
DM=CM,
故
CA=CM.
即证得解法4中“a=b”,后续易证FD=1(过程略).
3.5 四品题目——变式拓展,探寻真味
例1中的手拉手模型是有限制的.笔者思考适当放宽条件,如将“点D在BC的延长线上”改为“点D为平面内任一点”,或将条件“等腰直角三角形”弱化.
变式1 如图10,△ABC为等腰直角三角形,∠CAB=90°.在平面内取一点D,以AD为腰作等腰Rt△ADE,联结EC和BD,交于点H;AH,ED的延长线相交于点G,F是线段DG上的点,且∠DHF=∠DAH.若GF=2,EF=4,求FD的长.
解题思路 新交点H是例1中的点C吗?与点A有什么联系?由手拉手模型易得△DAB≌△EAC(如图11),过点A分别作对应边BD和CE上的垂线段AN和AM,AM=AN,AH为∠EHB的平分线,则
∠EHA=∠BHA=∠GHD=∠GHC.
由△DAB≌△EAC,得
∠BDA=∠CEA,
从而
∠DHE=∠DAE=90°,
故点D,E,A,H共圆,则
∠EDA=∠EHA=∠DHG.
由条件∠DHF=∠DAH,得
∠FGH=∠FHG,

教学说明 改变点D的位置,不再受BC延长线的束缚后,只要手拉手模型依旧发挥作用,结论依旧成立.例1只是一种特殊情况,变式1更具一般性.
变式2 如图12,△ABC为等边三角形,平面内取一点D,以AD为边作等边三角形,联结EC和BD,交于点H,AH,ED的延长线相交于点G,F是线段DG上的点,且∠DHF=∠DAH.联结HE,若GF=2,EF=4,求FD的长.

图12 图13
变式3 如图13,△ABC为等腰三角形,在△ABC所在平面内取一点D,以AD为腰作等腰△ADE,使得∠CAB=∠DAE,联结EC和BD,交于点H,AH,ED的延长线相交于点G,F是线段DG上的点,且∠DHF=∠DAH.若GF=2,EF=4,求FD的长.
教学说明 变式2和变式3的求解可参考解法1~3.通过条件一再弱化,变式3中的条件比例1中的条件更加一般化.
3.6 五品变式——探寻出题意图
变式3中只要手拉手模型成立,即得△DAB≌△EAC和点D,E,A,H共圆,通过证明AH为∠EHB平分线和圆周角定理,得∠EDA=∠DHG.加上∠DHF=∠DAH,可得等腰△GFH.又由四点共圆所得圆周角相等,可证∠DHF=∠DEH,可得△FEH和△FDH子母型相似,即得FD的长度为1.
去掉例1条件中的种种转化,回到最基本的几何图形,即试题的出发点,犹如品茗问产地.如图14,题目条件可简化为两点:①∠FHD=∠HEF,利用子母型相似得到FH是FD与EF的线段比例中项;②∠FHG=∠FGH,利用等腰三角形,将FH换成FG,最终将FH,FD,FE转化到一条直线GE上.

图14
由此可知,若将题目中的条件GF=2,EF=4调整为点F是GE的黄金分割点,则可得点D为EF的黄金分割点.这样的编题、改题的探索建立于对试题本质的探索.
4 教学反思
4.1 夯实基础知识,熟悉几何条件之间的转化
当解题由一个步骤推进到另一个步骤时,其实就是知识点之间的联系与生成[2].例如,例1难度较大,条件也较为复杂,但解题离不开对基础知识和基本技能的熟练掌握.学生只有夯实每一个知识点,熟悉知识之间、知识结构之间的联系,才能通过转化条件,建立起条件知识与结论知识之间的桥梁.
4.2 注重一题多解,培养发散思维
当一道题存在多个解法时,其实就意味着不同解法的知识点之间存在逻辑联系或对应关系.例1中条件知识转化为四点共圆和子母型相似后,产生了完全不同的4种解法.教师应注重引导学生总结归纳不同方法的本质和特点.不同的解法源于看问题的角度不同,思考途径不同,但都能起到复习知识点、开阔思路、发展思维的作用.
4.3 探索本质,突破出题意图,反向增进解题能力
罗增儒教授曾提出,教师的核心竞争力就是解题的能力.教师除了解题教学外,更要研究题目,通过弱化条件、一系列的变式等,探索图形元素之间的本质联系.只有触碰到出题本意,才能在此基础上对题目做出更好的改变,从而反向培养解题能力.
4.4 增强推理能力、几何直观,促进核心素养发展
解题活动的核心价值是掌握数学.教学重视对学生逻辑思维能力的培养,让学生面对复杂条件时,能有条理地思考,学会分析条件、转化条件.教学中注重引导学生在推理的过程中,结合几何直观寻找思路,用严谨的、理性的思维解决问题,最终促进学生核心素养的发展.

