一类圆锥曲线与多个三角形组合问题的解法探究
丁 晨
(海宁市高级中学,浙江 海宁 314400)
解析几何题是全国数学高考卷和以往浙江数学高考每年必考的题型,选择题、填空题和解答题中都有考查解析几何知识点的题目,难度从中等到较难.其中选择题、填空题以考查圆锥曲线等平面图形的几何性质为主,学生的解题以小题小做为原则,讲究通性通法,探寻几何关系.圆锥曲线与多个三角形组合的解析几何问题在高考中频繁出现,这类问题通常具有相对复杂的几何性质,学生很难抓住几何关系进行求解.下面笔者以2023年全国数学新高考Ⅰ卷第16题和往年高考、高中学业水平考试(以下简称“学考”)等解析几何选择题、填空题为例,帮助学生厘清知识要点,构建知识网络,找寻思考路径,跨越思维障碍.
臭氧浓度及产量是评价一台臭氧发生器性能的重要指标之一。在额定流量为62m3/h(标准状态下)的条件下,随着臭氧功率的增加,臭氧浓度由80.9mg/L逐渐上升至135.4mg/L,与此同时,臭氧的产量从5.0kg/h上涨至8.4kg/h,说明臭氧发生器功率对臭氧浓度及产量具有显著的影响。这主要是由于臭氧的产生是利用交变高压电场使含氧气体产生电晕放电,电晕中的高能自由电子离解氧分子并聚合生成臭氧分子,因此,在流量一定时,臭氧的浓度及产量与臭氧发生器的功率基本上呈现为正相关。
(2023年全国数学新高考Ⅰ卷第16题)
审题分析 首先根据题目条件作出图象(如图1),发现图中除了双曲线之外,还有3个三角形,分别为Rt△ABF1、等腰△BF1F2和焦点△AF1F2.直角三角形与勾股定理相关,焦点三角形的边长与双曲线定义中的a,c相关.

图1
解题思路 根据题目条件,先设F2A的长度,然后表示出F2B,F1B的长度,根据勾股定理计算出F1A的长度,应用双曲线定义可把图中的线段F2A,F2B,F1A,F1B,F1F2全部表示为含a,c的表达式,最后应用余弦定理等建立a,c之间的关系式,求得双曲线离心率.

|F2B|=|F1B|=3m,
则
|AB|=5m.
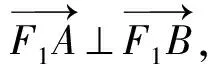
|F1B|2+|F1A|2=|AB|2,
故
|F1A|=4m.
应用双曲线定义|F1A|-|F2A|=2a,可知
4m-2m=2a,
即
a=m,
亦即
|F2B|=|F1B|=3a.
在△F1BF2中,应用余弦定理得
在Rt△ABF1中,
从而
从而
即
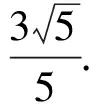
在利用多个三角形建立等量关系时,还可以用如下方法:
从而
在Rt△ABF1中,
因为cos∠F1AF2=cos∠F1AB,所以
从而
故
解法分支2 在△F1AF2中,应用余弦定理得
在Rt△BF2O中,
因为cos∠AF2F1=-cos∠BF2O,所以
从而
一是加强政府监管。强化对工程建设全过程的质量安全监管,加强对关键工序和主要分部分项工程的验收环节的监督检查;加强对监理单位的履职情况的检查,充分发挥监理单位在质量控制中的作用;加强对工程质量检测管理,严抓建筑材料和实体结构的取样、送样检测等环节的真实性,严厉打击出具虚假报告等行为。
即
解题反思 此题紧紧围绕与双曲线相关的几个特殊三角形的几何性质,涉及双曲线的定义、三角形的边角关系及它们之间的联系,一般应用的知识点是圆锥曲线定义、勾股定理、余弦定理等三角函数知识[1].计算过程抓住变量的个数与等量关系的个数,通过合理的消元达到最终的求解目标.考查学生根据题意的作图能力和几何条件之间的转换能力,还需要一定的数学运算素养.
针对目前的市场形势,国内出现了两种CDM开发模式。一是先签订减排量购买协议,由买家承担前期开发成本和风险的双边模式。二是由业主承担前期开发成本和风险、待项目注册成功后再寻找买家的单边模式。
圆锥曲线和多个三角形组合的解析几何选择题、填空题在历年的高考、学考中屡次出现.接着再看几道例题.
例2 已知椭圆C的焦点为F1(-1,0),F2(1,0),过点F2的直线与C交于点A,B.若|AF2|=2|F2B|,|AB|=|BF1|,则C的方程为
( )
(2019年全国数学高考Ⅰ卷理科试题第10题)
审题分析 首先根据题目条件作出图象(如图2),发现图中除了椭圆之外还有3个三角形,分别为等腰△ABF1、焦点△AF1F2,△BF1F2,这些三角形的边、角都与椭圆的a,c(其中a为椭圆长轴长的一半,c为焦距的一半)相关[2].
第二个关键点就是将传统电视媒体与新媒体之间进行有机结合。因为电视媒体的播出时间方面有着较大的限制,在网络之中进行直播也要按照预先设定的时间,但是当下人民群众的整体生活节奏越来越快,正因如此固定时间播出的方法很难被人们所接受。而从新媒体的角度来看,其在播出方面不会受到时间因素以及空间因素的制约,能够以相当快的速度完成信息的传播。在此基础之上电视媒体可以通过开通公众平台的方式,首先将新闻信息通过较为便捷的方式传递给观众,预先将新闻的重点告知观众,通过这种方式达到吸引观众注意力的效果,而且在这样的背景之下负责电视节目采编工作的相关工作人员一定要在第一时间掌握信息,并且确保信息的准确度。

图2
解题思路1 根据题目条件,先设F2A的长度,表示出F2B,F1B的长度,应用椭圆定义可把图中F2A,F2B,F1A,F1B,F1F2全部表示为含a,c的表达式,最后应用余弦定理等建立a,c之间的关系式,求得椭圆的方程.
解法1 令|AF2|=2|F2B|=2m,则
|BF1|=3m.
由椭圆的定义,得
|BF1|+|BF2|=4m=|AF1|+|AF2|,
2.2 CU检测和RT-3DE检测结果中RAA、RVDd、ΔIVC比较 RT-3DE检测结果中RAA、RVDd值明显高于CU检测结果,ΔIVC值明显低于CU检测结果,组间比较差异有统计学意义(P<0.05),RT-3DE测量数据的变化幅度更明显,见表2。
因为cos∠F1BF2=cos∠F1BA,所以
|AF1|=2m,
解法1 因为AP∥BF,由对称性可知直线AP过左焦点F1,则
|AF1|=|AF2|=2m=a,
在△AF1F2和△ABF1中,
因为cos∠F1AF2=cos∠F1AB,所以
解题思路1 根据题目条件知AF,BF,AF1,BP,BF1的长度都为a.设PF1的长度为2x,应用椭圆定义可知FP的长度.在△BPF1,△AFF1,△APF中,分别用a,c,x表示3个相等的cos∠BPF1,cos∠F1AF,cos∠PAF,3个参数建立两个等量关系,消去x即可得到a,c之间的关系,进而求得椭圆的离心率.
从而

解题反思 此题是以椭圆为基础的解析几何问题,这里出现的3个三角形都很特殊,具有较为明显的几何特征,解题思路围绕椭圆定义和余弦定理等应用.
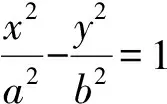
( )
(2010年浙江省数学高考文科试题第10题)
审题分析 首先根据题目条件作出图象(如图3),图中除了双曲线之外还有一个焦点△PF1F2和它的一条中线.如果把中线倍长后可以得到另一个△PF2Q,它的其中一个角大小为120°,3条边长都与a有关,最终这两个三角形的边、角都与双曲线的a,c相关[3].
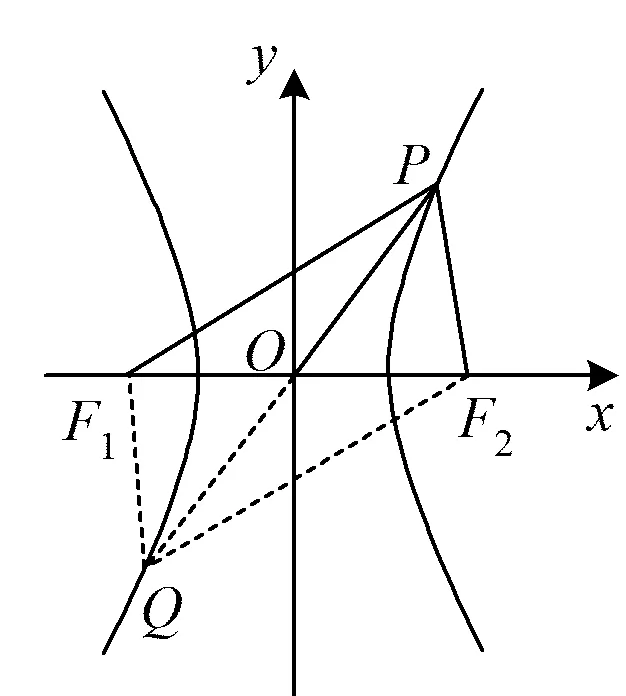
图3
解题思路 设PF1和PF2的长度分别为m和n,二者之差为2a.在焦点△PF1F2中应用余弦定理可以得到a,c,m,n之间的关系;倍长中线PO后得到△PF2Q,应用余弦定理可以得到a,m,n之间的关系;消去m,n可得a,c之间的关系,应用c2=a2+b2得到a,b之间的关系,求得双曲线的渐近线方程.
解 设|PF1|=m,|PF2|=n.在△PF1F2中,
采用统计学SPSS22.0软件进行数据处理。卡方用以检验计数资料,t值用以检验计量资料,经P值判定组间差异,以P<0.05具有统计学意义。
那老人脸一沉,说道:“你对他到底是真好还是假好,为什么连自己的身份来历也不跟他说?说是假好吧,为什么偷了爷爷二十年陈绍给他喝不算,接连几天晚上,将爷爷留作救命之用的‘玄冰碧火酒’,也拿去灌在这小子的口里?”
无论是对女司机肇事的特别关注,还是对整个女司机群体的调侃,即使够不上性别歧视,也是一种与实际情况不符的不公。不仅这样的说法不仅没有大数据的支撑,且许多数据还证明,无论是肇事的绝对量、相对量,还是事故的惨烈程度,男司机都远高于女司机。10月29日《中国青年报》的一篇报道披露,2016年男司机发生的交通事故与女司机相比,杭州市是6倍,南京市是2.4倍,而女司机肇事致人死亡数仅为男司机的五十分之一。其他数据也证明,交通肇事者中的男女比例明显高于司机中的男女比例。
遂行食管调搏检查进一步明确诊断。插管深度34 cm,起搏阈电压14 V,食管心电图见P波与QRS波无传导关系,表现出房室分离现象,考虑为左前分支室性心动过速。尝试行心房刺激终止心动过速。首先采用频率为250次/min的S1S1连续刺激可夺获心房,但未能终止心动过速,逐渐加快刺激频率,予频率300次/min的S1S1刺激,连续刺激10次,成功终止心动过速,转复窦性心律(图2)。心动过速终止后行12导联心电图检查,提示窦性心律,心率约128次/min,PR间期108 ms,QRS波时限为71 ms,电轴40°,无束支阻滞图形(图3)。
4b2=mn.
在△PF2Q中,
整理得
8a2=mn,
从而
4b2=8a2,
于是
解题反思 此题的图形是双曲线和它的一个焦点三角形,但是只有一个三角形难以得到最终结果,关键在于三角形中线的应用.三角形的中线通常用法是把它倍长,得到另一个三角形,这样就可以利用中线的长度求解.有时还可以得到平行四边形,应用平行四边形两条对角线长的平方和等于四边长的平方和等性质.此题归根结底还是转变为圆锥曲线和多个三角形的组合问题.
图4 图5
( )
(2021年1月浙江省数学学考试题第17题)
审题分析 图中有腰长与上底相等的等腰梯形,由对称性可知直线AP过左焦点F1,分割后产生焦点△AF1F,△BF1F,△PF1F和等腰△BF1P(如图5),它们的边长都与椭圆的定义相关.
解得
于是
|AF|=|BF|=|PB|=|AF1|=a.
令|PF1|=2x,则
|PF|=2a-2x.
在等腰△PBF1中,
在△AF1F中,
在△APF中,
从而
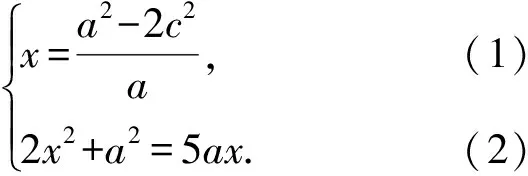
1)热含量(Heat Content,简称HC)的计算:本文综合考虑温跃层下界深度(吴晓芬等,2011)及资料的深度范围,将0~400 m深度的海洋温度平均值定义为海洋上层热含量值。
将式(1)代入式(2),得
解法分支1 在△F1AF2中,应用余弦定理得
4c4+a2c2-a4=0,
于是
4e4+e2-1=0,
即
除已治理的6 000 m河道外,对剩余河道,根据河道现状,河堤线走向基本维持现状,根据行洪需要对堤岸进行防护,并对河道进行疏浚,使河道断面满足20年一遇的防洪标准。
故选B.
整理得
解题思路2 利用等腰梯形“对角线相等”的性质,得到|PF|=|AB|=2b,应用椭圆定义可知PF1的长度.在△BPF1和△AFF1中,分别用a,b,c表示cos∠BPF1和cos∠FAF1,可得a,c之间关系,即可求得椭圆的离心率.
1961年2月5日,毛泽东听取中共浙江省委负责人汇报整风整社和省委召开扩大会议的情况。谈到生产队的规模问题,他说,我看一个生产队管不了这么多,太大了。在一个基本核算单位里,有富的、中等的、贫的,这就有问题,群众就不满意。小队就是过去的初级社。我看把小队改成生产队,明升暗降。原来的生产队变成生产单位和消费单位。毛泽东还交待浙江省委研究一下放在过去的初级社好,还是放在过去的高级社好?就是说,放在生产小队好,还是放在生产队好?[6]18他关于社队规模的谈话不仅对浙江,而且对全国其他地区的调查研究工作指明了方向。
解法2 因为AP∥BF,由对称性可知直线AP过左焦点F1,则
B组采用经伤椎椎弓根植骨联合椎弓根钉内固定系统治疗。患者伤椎复位及置钉方法与A组相同。C形臂X线机透视证实患者椎体复位满意后,行经伤椎椎弓根植骨。首先定位伤椎椎弓根,采用椎弓根螺钉置入的方法,经伤椎椎弓根将扩大器尾部置入到椎体的前2/3处,扩大椎弓根的高度和宽度,同时避免骨块进入椎管腔内,将人工诱导骨或纳米人工骨植入椎体前中部,并推压结实,植入完毕后使用明胶海绵填充洞口止血。C形臂X线机透视植骨效果满意后冲洗切口,置引流管,缝合切口。术后患者卧床3 ~ 5周后佩戴支具下床活动,4个月后去支具活动。
|AF|=|BF|=|PB|=|AF1|=a.
在等腰梯形AFBP中,
|PF|=|AB|=2b,
则
|PF1|=2a-2b.
在等腰△PBF1中,
在△AF1F中,
因为cos∠BPF1=cos∠F1AF,所以
从而
2c2=ab.
消去b,得 4c4+a2c2-a4=0,
于是
4e4+e2-1=0,
即
故选B.
解题反思 此题的模型是椭圆和等腰梯形,通过分割等腰梯形回到椭圆和多个三角形组合,既要利用好等腰梯形底角相等、对角线相等的性质,又要运用三角形中的余弦定理建立参数之间的关系.找好性质、找准关系是几何法解决圆锥曲线问题的关键.
总结这一组高考题、学考题,图形上都是圆锥曲线与若干个三角形的组合,因此几何法的解题思路就会一脉相承,找对合适的三角形就成了解题重要的突破口.
教学启示 解析几何的教学核心在于“解析”与“几何”,它归根结底是一个几何问题.因此,圆锥曲线的定义与它们的简单几何性质教学是重中之重,教师要善于结合初高中所学的平面几何知识,包括直线、圆、四边形、三角形等几何性质,以及它们所涉及的公式、定理,尤其是解三角形内容在圆锥曲线问题的应用中极为广泛.教师可以在知识和思维两个方面对几何内容进行总结,把上述知识网络化、结构化.在教学中,教师要让学生经历问题辨析、变式、拓展的过程,发现问题的本质,建立问题之间的联系;教师要指导学生建构思维导图,让学生用一个完整的思维体系去看待这些解析几何问题,提升学生的数学核心素养、创新能力和科学严谨的思维品质[4].
结束语 解题理论对于学生而言过于高深,较难领会和应用,但基于每一道题、每一组题解

