视形建型 结构关联
——以一道45°角几何问题的解题研究为例
徐建兵, 汪秀秀
(1.衢州市衢江区第一初级中学,浙江 衢州 324022;2.徐建兵名师工作室,浙江 衢州 324022;3.常山县龙绕初中,浙江 常山 324200)
1 问题背景
图形与几何是义务教育阶段学生数学学习的重要领域[1].几何图形中的角度问题又分为一般角与特殊角两大类.45°角是特殊角的典型代表之一,对于已知特殊角求三角形相关问题的研究具有一定的代表性.本文以一道45°角几何问题的解题研究为例,讲述运用图形特殊性的关联,在“形”与“型”的联系中形成解决问题的8种策略,这不仅有利于学生视野的拓宽、思维的开启和解题能力的提升,还有利于学生几何直观、空间想象和逻辑推理等核心素养的发展.
2 策略探究
2.1 问题呈现
例1 如图1,A,B,C在一条东西走向的公路沿线上,已知AB=2 km,BC=3 km,在B村的正北方向有一个D村,测得∠ADC=45°.现将△ADC区域规划为开发区,除其中4 km2的水塘外,其余均为绿化用地,试求绿化用地的面积.

图1
分析 含45°角的几何问题是几何与代数的综合性问题[2].从命题角度来说具有一定的代表性,有很高的研究价值,既体现了课程标准对基础知识、基本技能、基本思想和基本活动经验的要求,也是对教材基本概念的提炼与深加工,引导学生在观察几何图形时逐步学会用数学的眼光观察现实世界;在联系建构时培养学生会用数学的思维思考现实世界;在解决问题的过程中学会用数学的语言表达现实世界.因此,该问题解法策略的研究能用于评价学生的数学核心素养,是学生逐步形成适应个人终身发展和社会发展需要的数学思维品质和能力的关键[3].
2.2 策略呈现
视角1 建构等腰直角三角形模型.

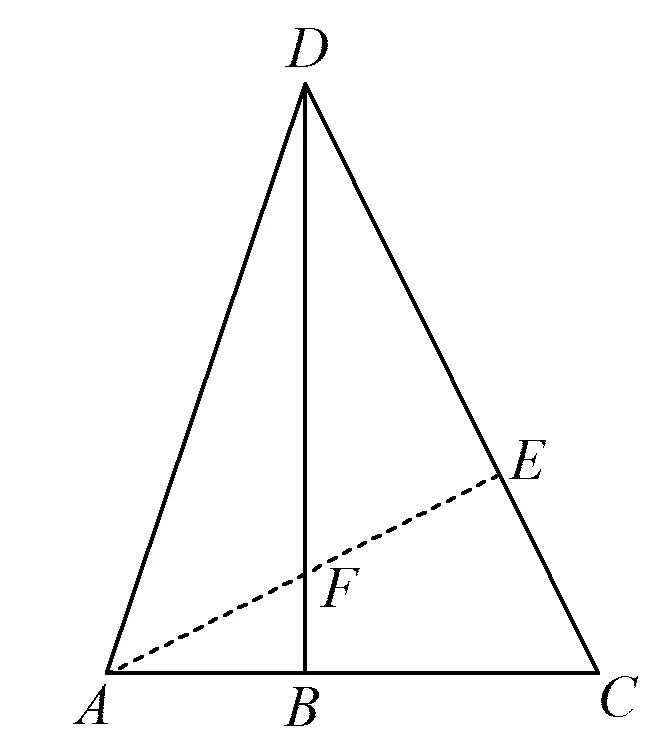
图2
进而
因为∠AEC=∠DBC=90°,∠C=∠C,所以
△DCB∽△ACE,
得
即
亦即
2x4-45x2+100=0,
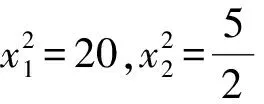

视角2 建构K字型全等模型.
解法2 如图3,过点A作AE⊥CD交CD于点E,因为∠ADC=45°,所以△ADE是等腰直角三角形.过点E作EH⊥AC交AC于点H,过点D作DG⊥EH交HE的延长线于点G,则四边形DBHG是矩形.由∠DEG+∠AEH=90°,∠EDG+∠DEG=90°,得

图3
∠EDG=∠AEH.
又∠G=∠EHC=90°,AE=DE,从而
△AHE≌△EGD(AAS),
得
AH=GE,HE=DG.
因为∠DEG=∠CEH,∠G=∠EHC=90°,所以
△DEG∽△CEH,
从而
设DG=x,则
BH=DG=EH=x,
又因为AB=2,BC=3,所以
AH=GE=2+x,HC=3-x,
得
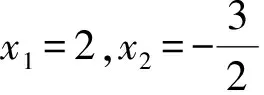
EH=2,GE=4,
于是
BD=6,
进而所求面积S=15-4=11,即绿化用地的面积为11 km2.
评注 视角1利用勾股定理求解会出现4次方的高次方程,利用相似可以弥补这一不足.视角2先由45°角联想建构等腰直角三角形,再由斜直角联系建构K字型全等,观察题中发现还有△DEG∽△CEH的图形关系,综合运用几何性质得以求解.K字型全等不仅在此题中能发挥其优势,在很多平面直角坐标系问题的解决中更加能体现它“化斜为正”的优势,已成为初中阶段坐标与图形问题解决的重要桥梁.
视角3 建构矩形半角模型.
解法3 如图4,分别以AD,DC为对称轴作点B的对称点F,E,使△DFA≌△DBA,△DEC≌△DBC;再过点C作CH⊥DC交DA的延长线于点H,从而△DCH是等腰直角三角形;过点H作HG∥DE分别交EC和DF的延长线于点G,I.由∠ADC=45°知∠FDE=90°,又∠E=∠AFD=90°,HG∥DE,从而∠G=90°,于是四边形DEGI是矩形.因为∠E=∠G=∠DCH=90°,所以

图4
∠HCG+∠DCE=90°, ∠CHG+∠HCG=90°,
得
∠DCE=∠CHG.
又因为DC=HC,所以
△ECD≌△GHC(AAS),
得
CE=HG,DE=CG.
设BD=x,则
DF=DE=GC=IG=x,
因为AB=2,BC=3,所以
BC=CE=HG=IF=3,
AF=AB=2,HI=x-3.
又因为∠I=∠AFD=90°,所以
AF∥IH,
得
△DFA∽△DIH,
从而
即
解得x1=6,x2=-1(舍去),从而BD=6,于是所求面积S=15-4=11,即绿化用地的面积为11 km2.
评注 视角3是延续视角2的K字型全等,选择过点C作垂直构造等腰直角三角形,这也揭示了此类问题构造等腰直角三角形的一般方法(过45°角对边的某一顶点作另两边的垂线建构等腰直角三角形).不同的建构方法会影响问题解决的计算难度,解题时应充分考虑计算的便利.从构造的结构和解题的过程都可以看出视角3较为复杂,需要视“形”建“型”,根据等腰直角三角形建构矩形半角模型,再结合K字全等与A字相似得以求解,这也体现了基本图形或基本图形关系在联系建构解决问题中的重要性.
视角4 建构正方形半角模型.
解法4 如图5,分别以AD,DC为对称轴作点B的对称点F,E,使△DFA≌△DBA,△DEC≌△DBC,再延长FA和EC交于点G.由∠ADC=45°,知∠FDE=90°,又∠E=∠F=90°,从而四边形DEGF是矩形.因为DE=DF,所以四边形DEGF是正方形.设BD=x,则
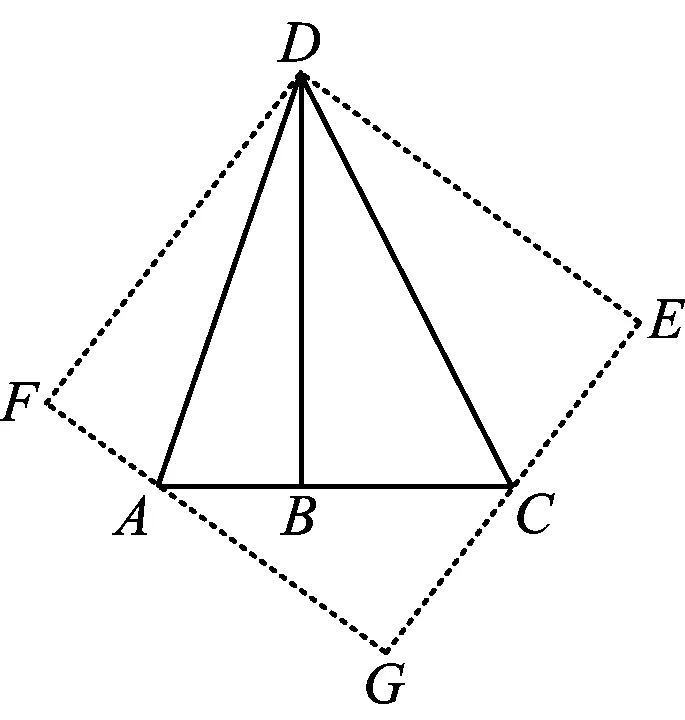
图5
DF=FG=EG=DE=x,
从而
AG=x-2,GC=x-3.
在Rt△AGC中,
AG2+CG2=AC2,
于是
(x-2)2+(x-3)2=52,
解得x1=6,x2=-1(舍去),于是BD=6,进而所求面积S=15-4=11,即绿化用地的面积为11 km2.
评注 视角4与视角3的矩形半角模型相比更加简洁.根据45°角联系建构90°角,顺势利用对称构造正方形半角模型,运用勾股定理求解.这是处理45°角转化为直角解决问题常用的方法之一,可以延伸到解决30°,60°和120°等特殊角的半角问题.
视角5 建构A字型相似模型.
解法5 如图6,延长BA至点E使得BE=BD,联结DE.因为BD⊥EC,所以△DBE是等腰直角三角形,从而

图6
∠E=∠CDA=45°, ∠C=∠C,
于是
△CDA∽△CED,
得
DC2=AC·EC.
由AB=2,BC=3,设BD=x,则
EB=x.
在Rt△DBC中,
DC2=DB2+BC2,
得
从而
9+x2=5(3+x),
解得x1=6,x2=-1(舍去),于是BD=6,进而所求面积S=15-4=11,即绿化用地的面积为11 km2.
评注 建构相似的图形关系是解决几何问题的重要策略.视角5从含45°角的三角形中的基本元素入手,联系构造新的含45°角的三角形,形成斜A字型相似的图形关系,再结合图形中的直角三角形相关性质求解.此类建构的优势是三角形边角等条件的相关性比较集中,在运算时能收到意想不到的效果.
视角6 建构一线三等角模型.
解法6 如图7,分别过点A,C作∠EAB=45°和∠FCB=45°,因为BD⊥EC,所以
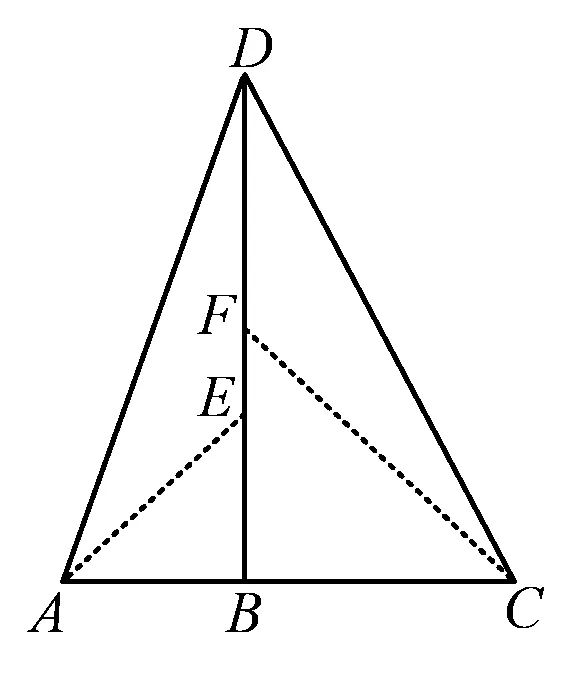
图7
∠AEB=45°, ∠CFB=45°,
得△ABE和△CBF都是等腰直角三角形,从而
BE=AB=2,BF=BC=3.
因为∠CDF+∠DCF=45°,∠ADE+∠CDF=45°,所以
∠ADE=∠DCF.
又∠AEB=∠CFB=45°,从而
∠AED=∠DFC=135°,
于是
△DAE∽△CDF,
得
设DB=x,则
DF=x-3,DE=x-2,
又

得
解得x1=6,x2=-1(舍去),于是BD=6,进而所求面积S=15-4=11,即绿化用地的面积为11 km2.
评注 相似的图形关系除了视角5的建构外,通常可以建构一线三等角模型的图形关系.视角6从含45°角的三角形中的基本元素入手,通过构造两个等腰直角三角形,联系建构一线三等角的图形相似关系,再结合图形中的等腰直角三角形相关性质求解.K字型全等是K字型相似的特殊图形关系,K字型相似则是一线三等角相似的特殊图形关系,厘清图形结构之间的关系,有利于在“形”与“型”的联系与建构中优化解题策略,提升解题能力.
视角7 建构圆模型.
解法7 如图8,构造△DAC的外接圆⊙E,联结AE,DE,EC,并过点E作EO⊥AC于点O,作EF⊥DB于点F.由AB=2,BC=3,知AC=5.又EO⊥AC,从而
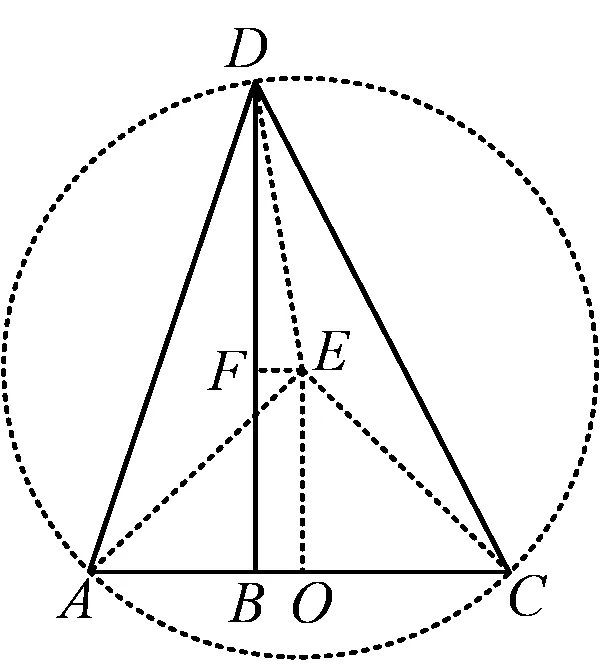
图8
因为∠ADC=45°,所以
∠AEC=90°,
从而
于是
又因为EF⊥BD,EO⊥AC,DB⊥AC,所以
∠EFB=∠FBO=∠EOB=90°,
得四边形EFBO是矩形,故
设DB=x,则
在Rt△DFE中,
DE2=DF2+EF2,
即
解得x1=6,x2=-1(舍去),于是BD=6,进而所求面积S=15-4=11,即绿化用地的面积为11 km2.
评注 由定角对定长会联想到定圆.视角7从含45°角的三角形中的基本元素入手,从三角形联想到三角形的外接圆,结合同弧所对的圆周角等于圆心角的一半,构造了90°的圆心角,然后再构造圆中的“两半一距”三角形,利用勾股定理即可求解.30°,45°和60°等特殊的角度构造圆心角时都能关联出特殊的等腰三角形,在解决问题时可以起到很好的效果.
视角8 建构正切和模型.

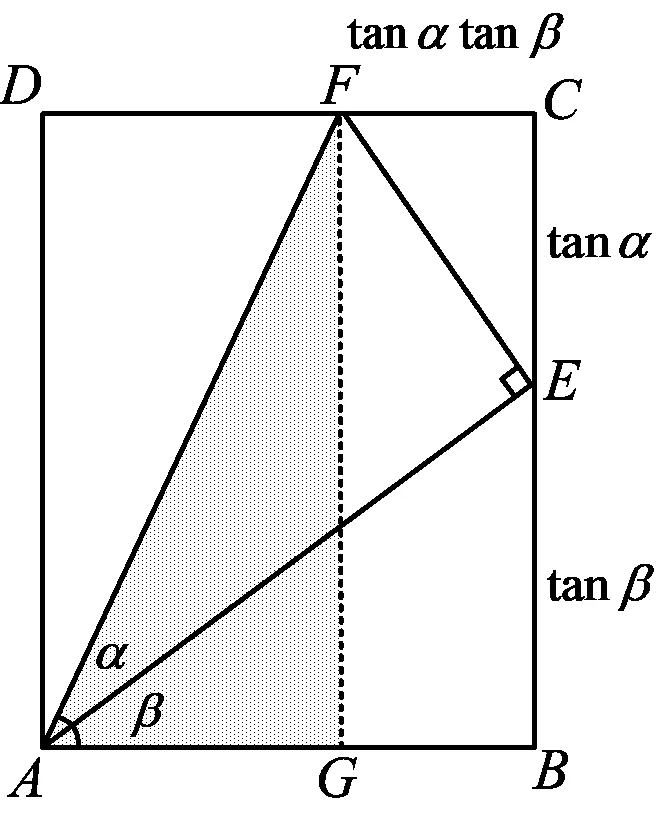
图9
CE=tanα,CF=tanαtanβ,
如图1,由AB=2,BC=3,设DB=x,则
因为∠ADB+∠CDB=45°,所以
解得x1=6,x2=-1(舍去),于是BD=6,进而所求面积S=15-4=11,即绿化用地的面积为11 km2.
评注 视角8从含45°角的三角形中的基本元素入手,从直角三角形联想到如图9所示,利用相似求正切和,将初中知识拓展到高中内容.笔者查看了人教A版《普通高中教科书·数学》(必修1)第5.5.1节“两角和与差的正弦、余弦和正切公式”的内容,教材中正切和公式是根据正弦、余弦和公式推导出来的,与视角8的相似构图推导截然不同,体现了同一高度的两种视角,这不仅拓宽了学生的思维,还让学生的知识体系更加丰富.
3 总结反思
初中阶段几何教学主要侧重学生对图形概念的理解,以及对基于概念的图形性质、关系和变化规律的理解,培养学生初步的抽象能力、更加理性的几何直观和空间想象力,感悟数学论证的逻辑,体会数学的严谨性,形成初步的推理能力和重事实、讲道理的科学精神[4].在复杂图形中抽象出基本图形和基本图形关系,在特殊元素中建构基本图形和基本图形关系是解决几何问题的关键,是学生核心素养的体现.“一题多解”和“多题归一”是一个相互联系、相互作用的综合整体,理解这些方法背后的原理和关联,有助于学生分析、解决问题的能力提升,也有助于学生思维灵活性、变通性、发散性和创新性的激发.史宁中教授在其访谈中阐述数学的结论是“看”出来的,不是“证”出来的,依赖的是数学直观,这是“三会”的现实表现.数学直观是一个人长期进行数学思维形成的,是逐渐养成的一种思维习惯.这个思维习惯日积月累就形成了数学素养[5].因此,在解决几何图形问题时,要重视基本图形和基本图形关系的提炼和运用,视形建型,用联系的观念建构数学模型解决问题.在教学活动中要关注学生从基本元素到基本图形的建构过程;要关注学生从基本图形到基本图形关系的建构过程;要关注学生知识本身到知识生长的建构过程.要让学生在体验中理解“形”与“型”的关联所在,从知识的宽度与深度进行拓展延伸,让学生理解知识的发生、发展和关联.在帮助学生建构知识体系的同时,优化解题策略,让学生有“居高临下”“一览众山小”之感,在以不变应万变的解题中提升学生的数学核心素养.

