人工智能与数学教育漫谈

张景中

(广州大学计算科技研究院,广东 广州 510006)

1 机遇与挑战

教育信息化涉及千家万户,这其中蕴含着巨大的机遇,也受到普遍重视,但多年来没有取得预期的效果.回顾20世纪八九十年代,出现过很多教育软件的大公司,但现在大都已经不见了.有没有取得预期的成果,关键在于优质数字教育资源的创建、应用和共享.2011年5月,乔布斯提出疑问:为什么计算机改变了几乎所有的领域,唯独对学校教育的影响小得令人吃惊?

从2011年到现在已经十几年过去了,虽然情况有了很大的变化,但是离大家的预期还相差很远.2017年6月,国务院发布《新一代人工智能发展规划》指出:中小学阶段要全面开展人工智能教育,构建新型教育体系.当时的网上出现各种各样的消息和广告,“教育+人工智能”刮起了一股旋风,非常热闹.但是现在回头看这些内容中有哪些在教育上、在学校里得到了认可?很少,这方面的进展还是非常艰难.

2 人工智能与数学间的关系

2.1 人工智能的基础是数学

最近人工智能有了一个重大的突破,即ChatGPT,后来进一步发展为GPT-4,他能够和人进行像人一样的谈话.问他问题,他就回答;让他画个图,他会画个图还能理解这个图,甚至可以用他来写文章、写诗,还可以做广告策划等.国内也推出了像文心一言、通义千问等类似的软件.这个ChatGPT代表了当前先进的自然语言处理技术与对话系统技术,其智能水平不断提升,最终达到与人类完全自然的对话交互.这意味着人工智能的又一次重大突破,将为我们的生活与工作带来深远的影响与变革.

2.2 人工智能促进数学教育发展

人工智能促进数学教育的发展至少表现在以下两个方面:1)有了人工智能,数学和数学教育自然而然地得到了更多人的重视.在人工智能的相关培训班上,要学不少的数学,包括统计概率、基本逻辑、形式逻辑等.2)推动了智能化的动态数学环境的创建,开发出了更丰富的个性化学习资源.当然,这方面仍然需要积极而慎重的实验和探索.笔者认为要重视两个方面,即优质的数字教学资源和操作环境的智能化.后一个方面是更为基础的,因为数字教学资源的开发、应用、获取、共享、优化和升级都要在一定的操作环境中实现.智能化的操作环境可以让开发者事半功倍,轻松实现其教学设计.所开发的资源应交互性强,易于管理和传送,便于重复使用,有利于资源的可持续优化发展.

3 人工智能促进数学教育的基础:智能化动态数学操作环境

智能化动态数学操作环境方面,最早的突破是20世纪80年代美国的几何画板软件.现在我们的网络画板也提供了智能化的操作环境,做出了很多原来不敢想的东西.当然这种画板不止一种,互相可以取长补短.下面笔者以网络画板为例做进一步的说明.

网络画板操作环境以理解题意、解题、判题为发展方向,其功能表现在多个方面,包括写数据、画图、图形测量、数值与符号计算、编程;网络画板还可以支持课堂演示,进行交互推理;此外,网络画板还支持“变”,数学对象的表示、数据等都可以是动态的、可变化的;甚至网络画板还是智能的,如笔者画一条线段,把鼠标放到接近线段中点的位置时,它就会猜想“是不是要作个中点”,这时笔者只要一点鼠标,它就能作出线段的中点,体现了初步的智能化.在这个基础上,笔者把线段缩短或拉长,中点仍然是中点.对于学习数学来说,在这种图形的动态变化中,测得的线段长度的数据也是动态变化的,会跟随着我们的拖动而变化.这种动态变化的图形,可以提高学生的学习兴趣、减轻教师的负担.借助网络画板等这类操作环境,能很快作出上述图形.在之前没有发展动态数学软件的时候,教师要想作一个这样的图,往往需要花一两个小时进行程序编写等工作才能完成.智能要随机应变,动态化是智能化的起步,因此研究智能软件需要耐心地、持续地发展,要有工匠精神.天下难事,必作于易;天下大事,必作于细.我们研究网络画板30多年,一步一步做起来很不容易,因为每一个细节都会影响教师的操作,这一点笔者深有体会.

网络画板作为一个智能化的平台,自动推理技术在数学教育中有很强的应用潜力.我们在这方面做了30年的研究,也取得了一系列的成果,但近年来国际上在这方面没有什么新进展,尽管如此也远远超过了现在ChatGPT的推理了.

例如,对于“三角形的3条高交于一点”这一问题,用网络画板先作△ABC的两条高交于点F,再延长CF交AB于点G(如图1).

图1

作出这样一个图后,如果我们让网络画板去证明CG是边AB上的高,只需要0.05秒,还能得到很多相关信息.在随后产生的推理库中,它会显示许多推理结论,比如与相似三角形相关的结论一共有42条.我们还可以进一步选择一对相似三角形,让它进一步解释为什么相似,轻点鼠标右键,还可以输出证明.由此可见,在几何推理方面,我们能从小数据产生大数据,根据现有的几个条件画出来,软件就能推理出许多的几何性质.网络画板还可以做像“蝴蝶定理”这些比较难的题目,还可以一题多解、交互推理.重要的是,这里的交互还包括人和计算机的交互.例如,人可以问:“这个问题可能要用到什么公式?”计算机就会把这个公式给你推出来.笔者认为可以对这方面做进一步的研究,让它在教育上发挥更大的作用.

4 人工智能与数学教育融合还要从学科上下功夫:教育数学

数学教育不但要在人工智能平台上下功夫,使信息技术与学科深度融合,还要在数学本身上下功夫,让数学变得更容易.我们在这个方面做了几十年的思考和教学实践.1976年阿蒂亚曾提出,如果我们积累起来的经验要一代代传下去,就必须不断努力把它们简化和统一;过去曾经是成年人困惑的问题,在以后的年代里,连孩子们都能容易地理解.他认为数学应该是越变越容易,应该是不断改进、不断发展的.那么具体来说是如何发展的,又是如何处理教学难点的?通常的做法是难了不学.长期以来有个说法,删繁就简,难的就把它删掉.但是笔者认为难的不能简单地一删了之,难的东西可能更重要.我们要研究的是把它变容易,这也是最理想的.什么叫变容易?怎样才能变容易?笔者的体会是:熟悉了就容易,简单了就容易,想通了就容易,直观了就容易.这就是大道至简的道理.它应当是简单的,如果不简单就说明有新的东西没有被发现;如果基本的东西又很复杂,就说明我们还没有发现更好的方法,同时还需要思考如何从学生的头脑出发来找新的概念、新的方法.因此,笔者认为熟悉了就容易,要温故知新;简单了就容易,要化繁为简;想通了就容易,要讲清道理;直观了就容易,要用智能动态的环境,要用信息技术.

例如,三角函数有很多定义方法,微分方程、函数方程、无穷级数、坐标之比、单位圆坐标、三角比、圆的弦长,这些都可以定义三角函数,我们就找到了最容易理解的新的定义方法.小学生都知道矩形的面积等于长×宽,如长为3、宽为2的矩形面积,其实是等于3×2×一个单位正方形的面积(即1),如图2所示.

图2 图3

如果把矩形搞“歪”了(如图3),那么就变成了平行四边形,此时它的面积为“3×2×一个单位菱形的面积”.但单位菱形的面积不是1,需要打个折扣.如果我们给折扣起个名字,把一个角为A的单位菱形面积叫做sinA,那么就有了平行四边形的面积公式:S=AB·AD·sinA.

平行四边形面积取其一半,便得到三角形面积公式.图4中三角形的面积公式为

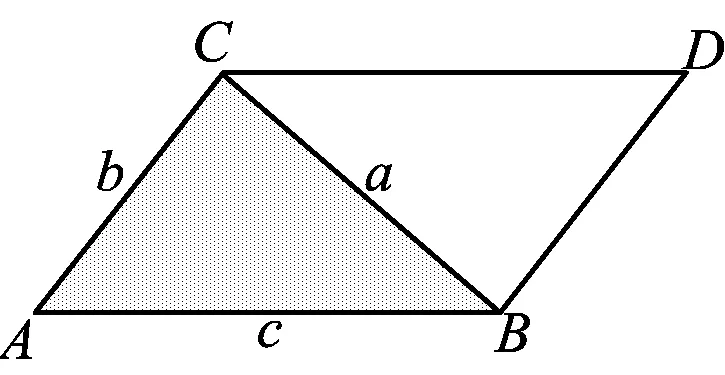
图4

于是就能得到正弦定理

这样,从小学知识出发很快就得到了高中才学习的正弦定理.如果我们用这种方法把它放在初中一年级去学,那么对学生的数学学习会有很大的促进作用.学生会感到学数学变得容易了.这是20世纪70年代笔者在新疆曾经做过的实验,到现在已经过去几十年了,还有很多学校在做这个实验,学生感到几何、三角都变容易了.

这说明在数学里面有很多的东西,现在看来很复杂很难,实际上是可以变简单的,我们要研究怎么把它变简单.

要解决数学教育的难题,我们需要内外“夹攻”,教育数学是从内部来攻破,人工智能则是从外部来攻破,后者给攻克数学教育难题提供了大好的机遇.“数学教育+人工智能”永远都是进行时,这项改革在我国有基础、有条件,既有国家重视,也有群众基础;既有发展空间,又有科学价值,无论从近期看还是远期看,都有巨大的效益,能大面积、大幅度地提高青少年的数学素养,创新人才大军也必将如长江奔腾,滔滔不绝.