基于动态改进遗传粒子群-BP的重型车NOx排放预测模型研究

钱枫,马骋,祝能,王明达,王继广,许小伟

(1.武汉科技大学汽车与交通工程学院,湖北 武汉 430081;2.中国环境科学研究院,北京 100012;3.中国汽车技术研究中心,天津 300300)

截止2021年,我国各类机动车保有量已达3.95亿辆,同比增长6.18%。而全国机动车排放的CO、HC、NOx、PM四种污染物总量为1 557.7万 t。其中,柴油车NOx排放量已经占到总量的80%,是空气污染的一个重要源头[1]。为了有效控制重型车排放对环境的危害,世界范围内制定了以欧盟、美国和日本为代表的三个排放标准体系。然而,这些标准体系受限于实际道路的影响,无法准确反映重型车在真实场景下的污染物排放水平[2]。

李昌庆等[3]利用PEMS采集大型客车尾气排放,利用BP网络对CO2、CO和NOx排放进行了预测,在算法选择上较为单一。Dai等[4]利用贝叶斯优化的LSTM对柴油机排放进行研究,与SVM和BP相比,基于贝叶斯优化的LSTM在不同工况下具有更好的预测精度。Wang等[5]采用融合算法和随机抽样组合神经网络进行研究,并与随机森林模型等对比,结果表明组合神经网络具有更高的拟合精度和预测精度,提供了一种新的预测分析思路。闻增佳等[6]为减少人为因素对RDE测试的影响,提出了GA-ACO优化的BP网络,并取得较好的NOx排放预测结果,但在具体参数调整思路上仅采用了简单的串行优化。Xu等[7]提出了一种ST-MFGCN融合网络,能够通过多种融合策略适应排放数据的变化波动,从宏观角度实现对划定区域范围内的车辆排放预测。Oduro等[8]使用CART和BMARS构建混合模型,但缺乏与其他神经网络预测模型的对比。Howlader等[9]采用集成 LSTM-RNN-GRU 实现了对轻型车辆 CO、NOx和 HC 排放的准确预测。

综上,PEMS、RDE等排放测试过程需要投入大量人力物力,同时,人为因素也会对排放预测研究过程有较大影响,而复杂的预测分析算法会大大增加计算负担。为了降低重型车排放测试过程中的经济投入、时间损失以及人为因素的影响,本研究在充分利用OBD采集的数据基础上,使用BP算法建立了一种重型车NOx排放速率预测模型;为了提高预测精度,引入遗传粒子群组合算法并对其改进,并利用PCA分析提取数据特征;另外,同步建立了其他9种NOx排放预测模型进行对比。

1 数据采集和预处理

1.1 数据收集和预处理

OBD可以实时收集车辆排放、运行状态等信息并上传至远程管理监控平台[10],也可以从远程管理平台导出历史数据进行分析。构建预测性能优良的模型需要大量高质量样本数据支持,并须对数据进行适当预处理,如数据筛选清洗、归一化等[11]。经过数据预处理,共获得了6 661 960条数据,并新增NOx排放率(mgas)和瞬时VSP比功率两项数据。

(1)

式中:ugas是排气成分密度与排气密度之比,设定为0.001 587[12];cgas,i是排气成分的瞬时浓度;n是测量次数;f是采样频率,本研究中取1 Hz;qmaw,i是瞬时进气质量流量;qmf,i是瞬时燃料质量流量。

VSP=v[1.1a+9.81arc tan(sing)+
0.132]+0.000 302v3。

(2)

式中:v为车速;a为加速度;g为坡度,由于所选车辆海拔变化不明显,故将坡度设为0。

为了让模型有更好的预测效果,防止预测模型出现过拟合[13],将原始数据的70%作为训练集、15%作为验证集、15%作为测试集进行划分;由于参数量纲存在差异,需要对原始数据进行归一化处理[14]。

(3)

1.2 相关性分析

部分参数,如油耗等,已被证实会对重型车NOx排放产生影响[15],其他参数是否会对NOx排放产生影响还需进一步分析。利用Pearson和Spearman系数可以分析其他参数对NOx排放的影响,系数为0.7以上表示变量之间存在较强的相关性[16]。

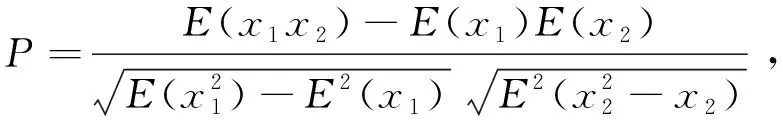
(4)

(5)

1.3 主成分分析

在模型输入参数选择时,多个参数之间存在相关性和耦合性,这会导致分析计算复杂,使结果产生较大偏差。利用PCA数据特征提取的基本方法,在PCA过程中,每个特征都是基于原始参数的线性组合[16]。

2 排放预测模型

2.1 BP神经网络

误差反向传播神经网络泛化能力强、非线性映射能力好,具有广泛的应用前景。选用BP网络构建重型车NOx排放预测模型,模型结构见图1。

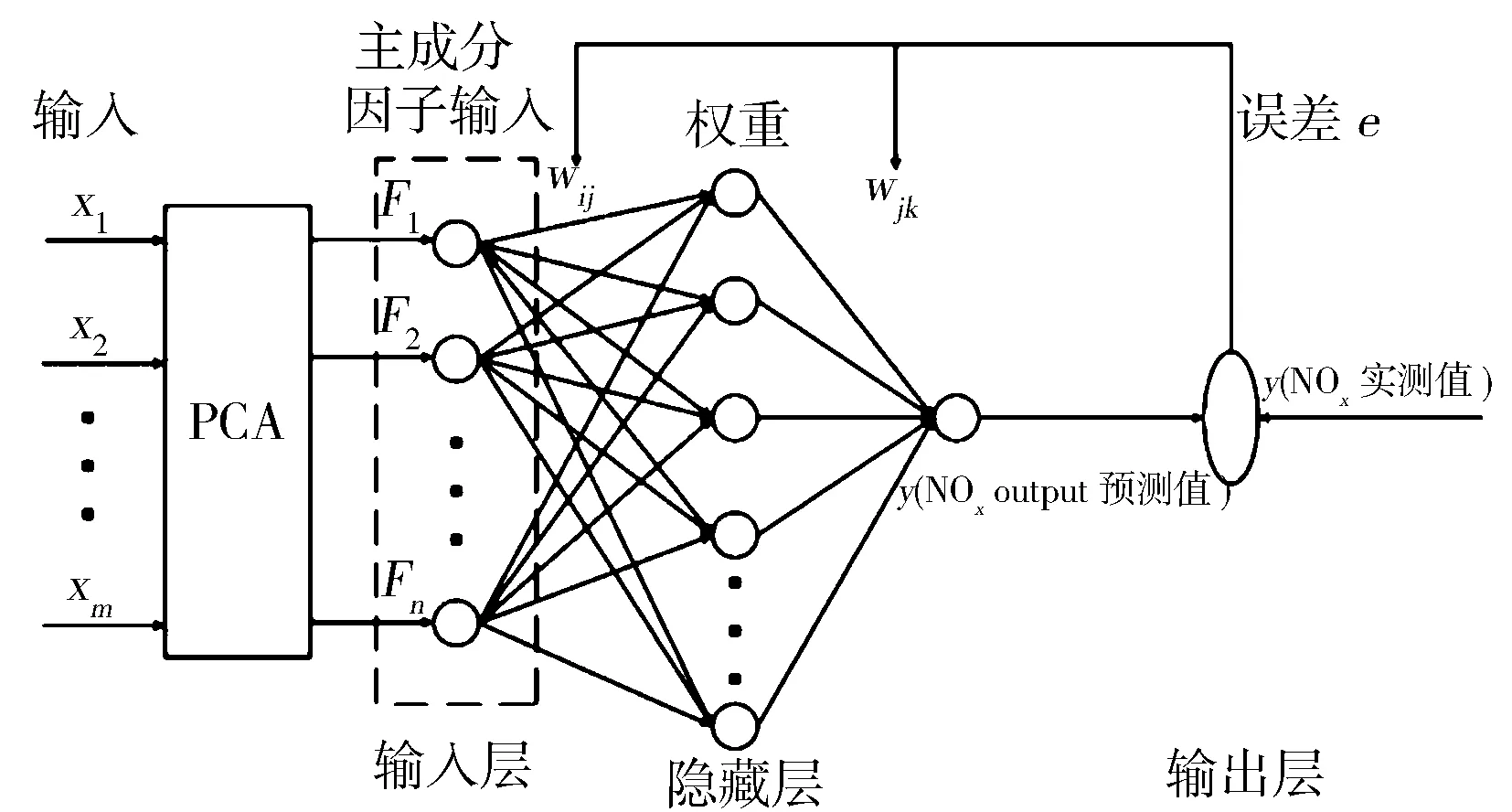
图1 BP神经网络结构

其中:F=(f1,f2,…fn)T(n=1,2,…n)为输入层;H=(h1,h2,…hn)T(n=1,2,…n)为隐藏层;y为输出层;wij和wjk为BP网络权重;隐藏层神经元个数可以由经验公式来确定[14]。

(6)

式中:H1是隐藏层中神经元的最终数量;a是输入层的数量;b是输出层的数量;c通常取1～10之间的值。本研究中输入为 11,输出为 1,c取[2,12]之间的值,这里设定为9。因此,BP网络的结构为11-14-1。BP网络也存在很多问题,在权重更新方面,很容易陷入局部最优;若求解目标复杂,易导致算法收敛缓慢。基于此,考虑利用遗传粒子群优化模型参数[17]。

2.2 粒子群算法

粒子群算法(PSO)源自鸟群觅食行为,通过共享群体信息实现个体最优解。PSO的每个粒子的位置是当前最优解Pbest,而种群的当前最优解Gbest也可以作为粒子的位置。在迭代过程中,粒子可以更新Pbest和Gbest,同时更新粒子的速度和位置[18]。算法求解如下。

1) 初始化m个d维度粒子所构成的群体,也就是Xi=(xi1,xi2,…xin)T。

2) 将Xi代入到给定的目标函数中,计算适应度数值。

3) 记录粒子个体的Pbest,持续迭代。

4) 在迭代过程中,记录粒子个体的Pbest和Gbest。

5) 更新粒子的速度和位置。

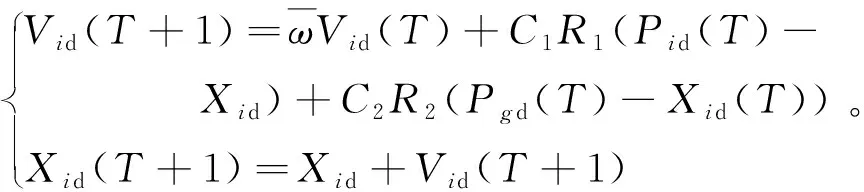
(7)

式中:T为某一时刻;ω为粒子群算法的惯性权重,一般设置为固定参数0.5,通过优化该参数,可以增强或削弱算法的全局搜索能力和局部寻优能力;Xid和Vid分别为第i个粒子的位置以及速度[19];Pid,Pgd为第i个粒子搜索的最优解和群体解;C1和C2为PSO的学习因子,一般设置为2;R1和R2则是介于0～1的均布随机数。

2.3 改进的遗传粒子群组合优化算法GA-PSO

遗传算法(GA)源自于生物进化中的优胜劣汰观念,模拟了自然界的进化过程[20],算法流程包括参数编码选择、定义适应度函数、选择、交叉和变异操作。

粒子群和遗传算法在很多细节上有相似之处,它们都利用种群优势寻找最优解,可以并行实现,算法性能稳定,但也存在问题。GA变异初期可以明显增强局部搜索能力,增加种群的多样性,但稳定后,GA变异操作会打破种群稳定的平衡,使种群迭代过程被迫停止[21]。而粒子群算法在寻找最优解的过程中存在大量低速聚集粒子,消耗大量计算资源,延缓后期收敛速度,导致PSO搜索陷入局部最优解[22]。为了充分发挥PSO和GA算法各自的优势,对PSO进行改进,并引入交叉和变异操作。

2.3.1 惯性权重ω

在粒子群算法中,ω是惯性权重。通过在初始阶段设定较大的数值,可以让粒子快速接近优势区域,从而增强算法的全局搜索能力。随着优势区域的逐渐缩小,再设定较小的ω数值,可以增强算法对局部区域的寻优搜索。通过动态调整惯性权重,可以兼顾全局寻优和局部搜索的能力:

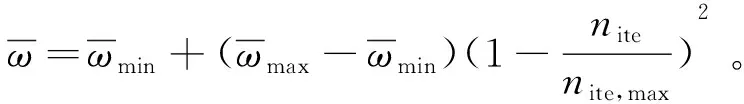
(8)

式中:ωmax和ωmin为设定的最大、最小惯性权重,一般取值分别为0.9和0.4;nite和nite,max为当前迭代次数以及最大迭代次数。本研究选择采用了抛物线递减策略,在算法初期快速收敛,逼近到最优解集空间。

2.3.2 学习因子C1和C2

PSO学习因子C1和C2会对算法的探索性和收敛性产生影响。若学习因子过大,易导致算法陷入局部最优而无法跳出;若学习因子太小,则易导致粒子出现“早熟”现象[23],无法达到最优解。为了实现算法平衡性和较好的探索性,需要动态调整学习因子C1和C2,改进如下:

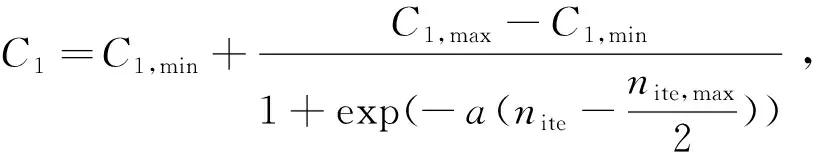
(9)

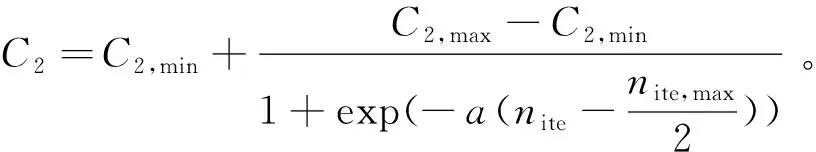
(10)

式中:C1,max和C2,max分别是学习因子C1和C2的最大数值,通常设置为2;C1,min和C2,min则是学习因子C1和C2的最小值,一般设定为0.1;a是rand(0,1)之间的随机数;nite是当前迭代次数;nite,max是最大迭代次数。

2.3.3 交叉、变异操作

在遗传算法的交叉和变异操作中,算法的收敛性能受到交叉概率和变异概率的影响。若概率值固定不变,可能会导致算法后期种群多样性降低,不利于收敛。为了改善该问题,利用自适应遗传算法的思想,给出交叉概率Pcrossover和变异概率Pmutation的理论依据:

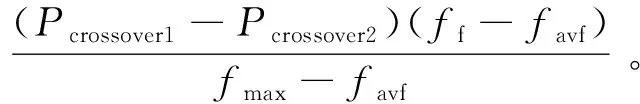
(11)

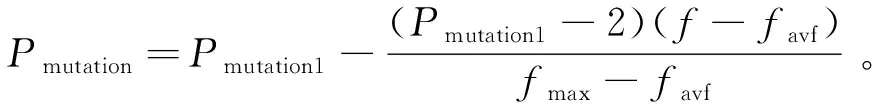
(12)

式中:ff是迭代过程中较大的个体适应度数值;favf是迭代过程中群体的平均适应度数值;fmax则是迭代过程中最佳的适应度数值;f则是个体的适应度。

引入遗传算法,计算个体适应度数值并排序;按一定比例对适应度较高的个体进行交叉、变异操作,产生新的子代。将新的子代与旧群体合并,并继续进行算法迭代,直至达到设定的阈值条件或达到最优适应度函数目标值。下面是动态改进的GA-PSO组合算法优化BP网络模型参数的流程步骤。

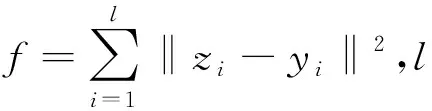
2) 计算粒子的适应度数值。

3) 对适应度数值进行大小排序,并且记录在这个迭代过程中的Pbest和Gbest。

4) 动态计算新的个体速度和位置以及ω,获得新种群。

5) 引入遗传算法,对群体中粒子执行交叉、变异操作,更新粒子速度Vid和位置Xid。

6) 交叉操作之后,将新的子体放入群体中,重复执行迭代过程。

7) 判定Pbest和Gbest是否已经达到最优解状态或者已经达到设定的迭代次数阈值,符合要求则跳出循环,输出网络参数最优解,否则继续执行上述流程步骤。改进的遗传粒子群组合算法优化BP算法流程见图2。

图2 改进遗传粒子群组合算法优化BP预测模型流程

3 预测模型结果分析

3.1 主成分分析和相关性分析

在进行PCA分析之前,需要对预处理的数据集进行KMO检验和Bartlett’s球度检验,以确定数据集是否支持PCA分析[24]。KMO检验用于评估数据集的多重共线性,若其值接近1,则说明数据集变量之间存在高度相关性;Bartlett球度检验则用于判断变量是否不相关[25]。KMO结果为0.771,该值大于0.5,而Bartlett球度的P值为0.020 4,该值接近于0,因此可知该数据集适合进行PCA分析。

通过计算分析部分数据的相关性,其相关性热力图见图3。由图3知,变量之间有较强的耦合性:例如车速、发动机扭矩百分比、发动机转速、加速度和瞬时VSP参数之间存在显著影响,其相关系数分别为0.44,0.57,0.51和0.82。同时,NOx排放速率、进气量、入口温度和出口温度之间也存在高度关联,对应的相关系数分别为0.91,0.88和0.77。若直接将变量作为排放预测模型的输入,会导致结果失真且误差较大。因此,需要利用PCA或LDA算法提取数据变量的特征,本研究选择PCA算法。

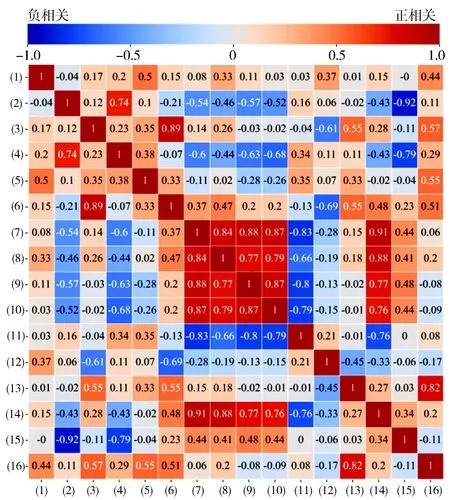
(1)—车速;(2)—大气压力;(3)—发动机扭矩百分比;(4)—摩擦扭矩;(5)—发动机转速;(6)—发动机燃料流量;(7)—进气量;(8)—入口温度;(9)—出口温度;(10)—发动机冷却液温度;(11)—实际尿素喷射量;(12)—瞬时油耗;(13)—加速度;(14)—NO排放速率;(15)—扭矩;(16)—瞬时VSP。图3 主成分贡献度热力图

从图4可以看出,经过PCA分析后11项因子的累计贡献率可以达到0.99以上,这表明主成分维度越高,经过分解重构的奇异值数据与原始数据之间的信息重叠性就越好。基于此,可以将这11项主成分因子作为预测模型的输入。通过进一步计算主成分载荷矩阵,可以分析主成分因子与变量之间的耦合程度。

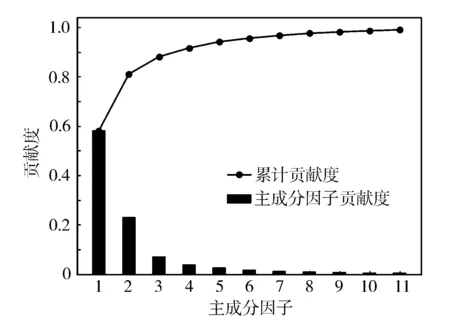
图4 主成分贡献度分布

3.2 测试函数结果分析

为了验证动态改进的GA-PSO算法有效性,选择4个常用的测试函数进行性能验证[26],设定测试函数迭代次数为150次。其中,f1为单峰函数,f2～f4均为多峰测试函数。

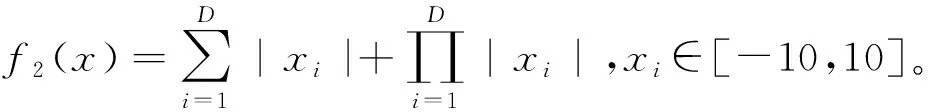
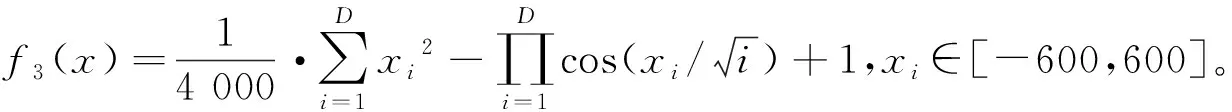
4) Ackley函数(f4)具有较大的搜索空间,形状复杂,并且存在周期性振荡,能够很好地评估优化算法的全局策略和利用振荡的特性,f4(x)=-20·

图5和图6示出测试函数的迭代曲线和适应度曲线。从图5可以看出,对于Sphere函数,PSO和GA的全局搜索能力较弱,容易陷入局部最优并过早停滞,相反,动态改进的GA-PSO组合算法在第30、第50和第110次迭代时能够跳出局部最优。对于Schwefel、Griewank和Ackley函数,动态改进的GA-PSO算法在设定的迭代次数内明显优于PSO和GA算法。GA在40～60次迭代后趋于平稳,PSO在Griewank函数中具有较好的优化能力,但仍弱于GA-PSO组合算法。对于Ackley函数,GA-PSO组合优化算法能够跳出局部最优解,在经过约60、80次迭代仍能继续逼近全局最优。

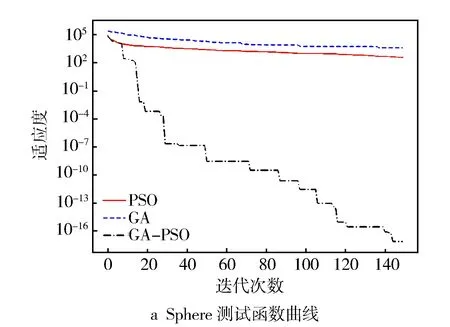
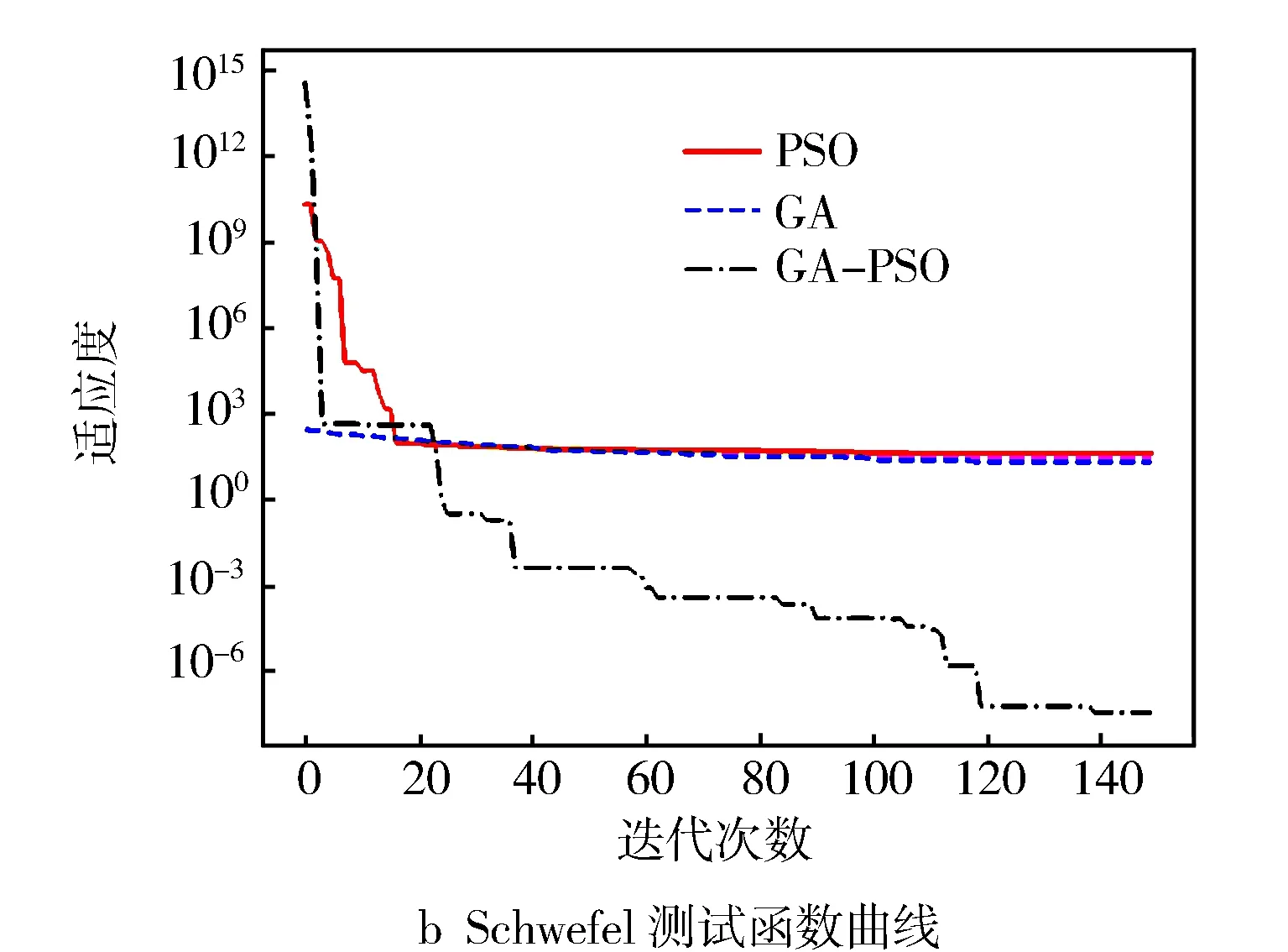
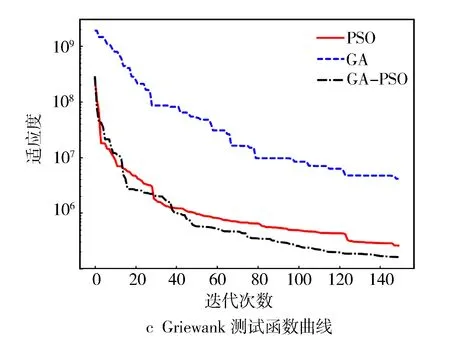
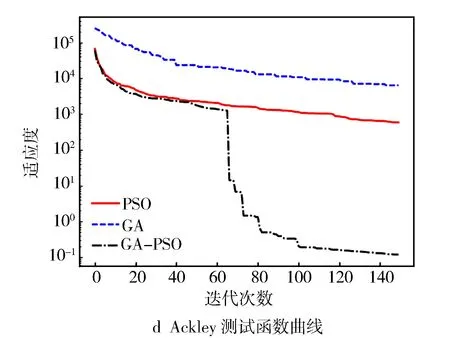
图5 测试函数的迭代图

图6 适应度函数迭代曲线

由图6的目标函数适应度迭代曲线可以看出,GA-PSO算法在允许的迭代次数内达到了0.92的目标适应度,具有更好的寻优潜力。GA和PSO算法在达到迭代次数之前趋于稳定,分别为0.87和0.89,表明其已经提前陷入局部最优解。将遗传算法的交叉、变异和选择操作引入粒子群迭代过程后,GA-PSO算法可以避免陷入局部最优解。在设定的迭代次数内,经过动态改进的GA-PSO组合优化算法相较于传统GA和PSO算法适应度分别提升了3.37%和5.75%,展现出了更好的全局搜索能力和更快的收敛速度。

3.3 排放预测模型结果分析

在预处理后的数据中选择15%作为测试集,其中NOx排放数据的柱状图见图7。NOx排放速率集中在0～300 mg/s,占比超过80%。而排放速率超过500 mg/s的数据则只占测试样本的2%。

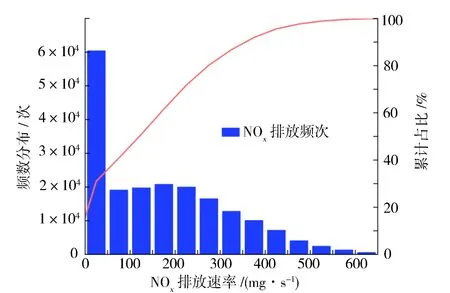
图7 NOx排放分布图

将提取主成分后的数据特征作为预测模型的输入,并以NOx排放速率作为预测输出。然后从测试机中随机选择一段相同且连续的样本数据段作为真实数值,以进行对比。同时为了验证基于改进遗传粒子群组合算法优化的BP网络在预测NOx排放速率方面的精准性,建立了BP、GA-BP、PSO-BP、RF-BP等共9种不同的排放预测模型以进行对比,各模型预测结果对比见图8。

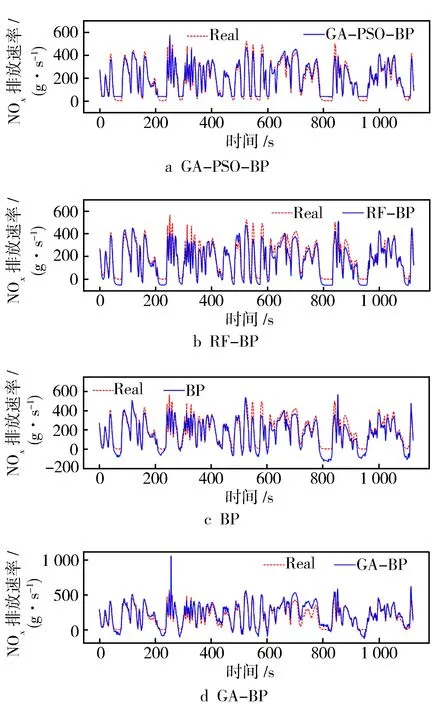
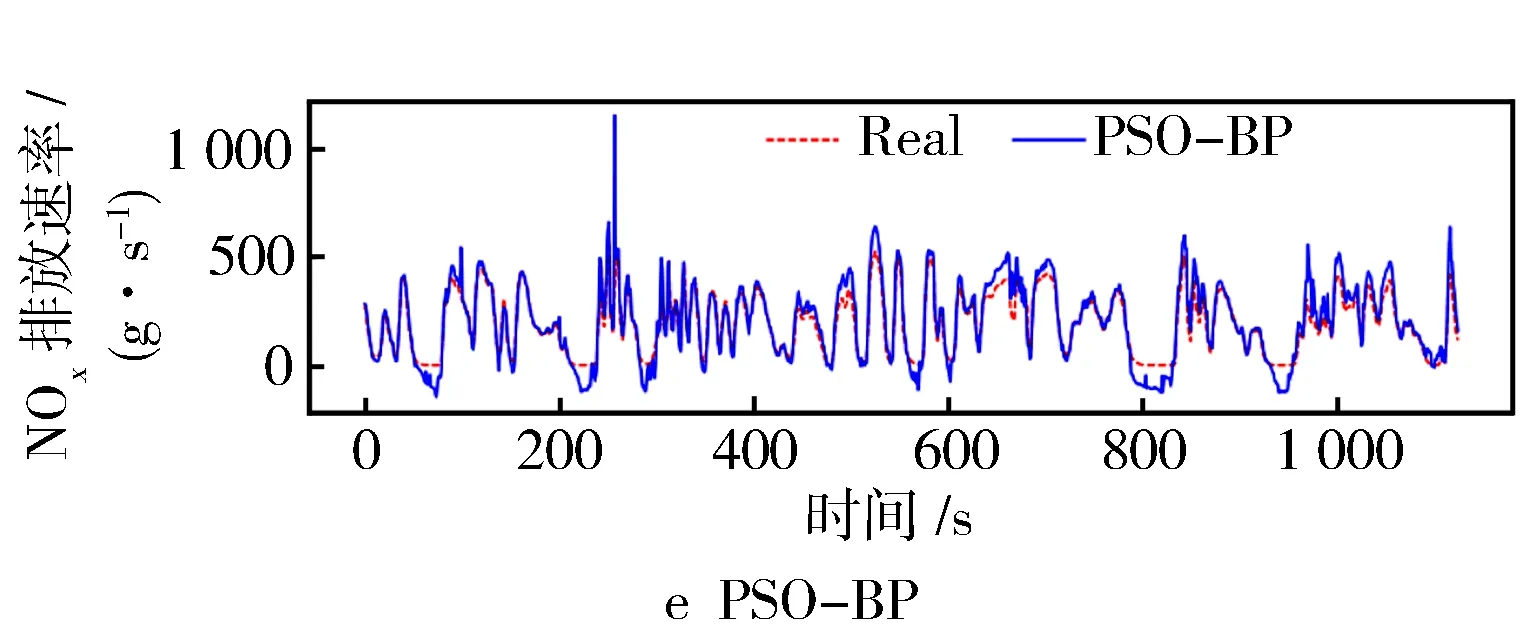
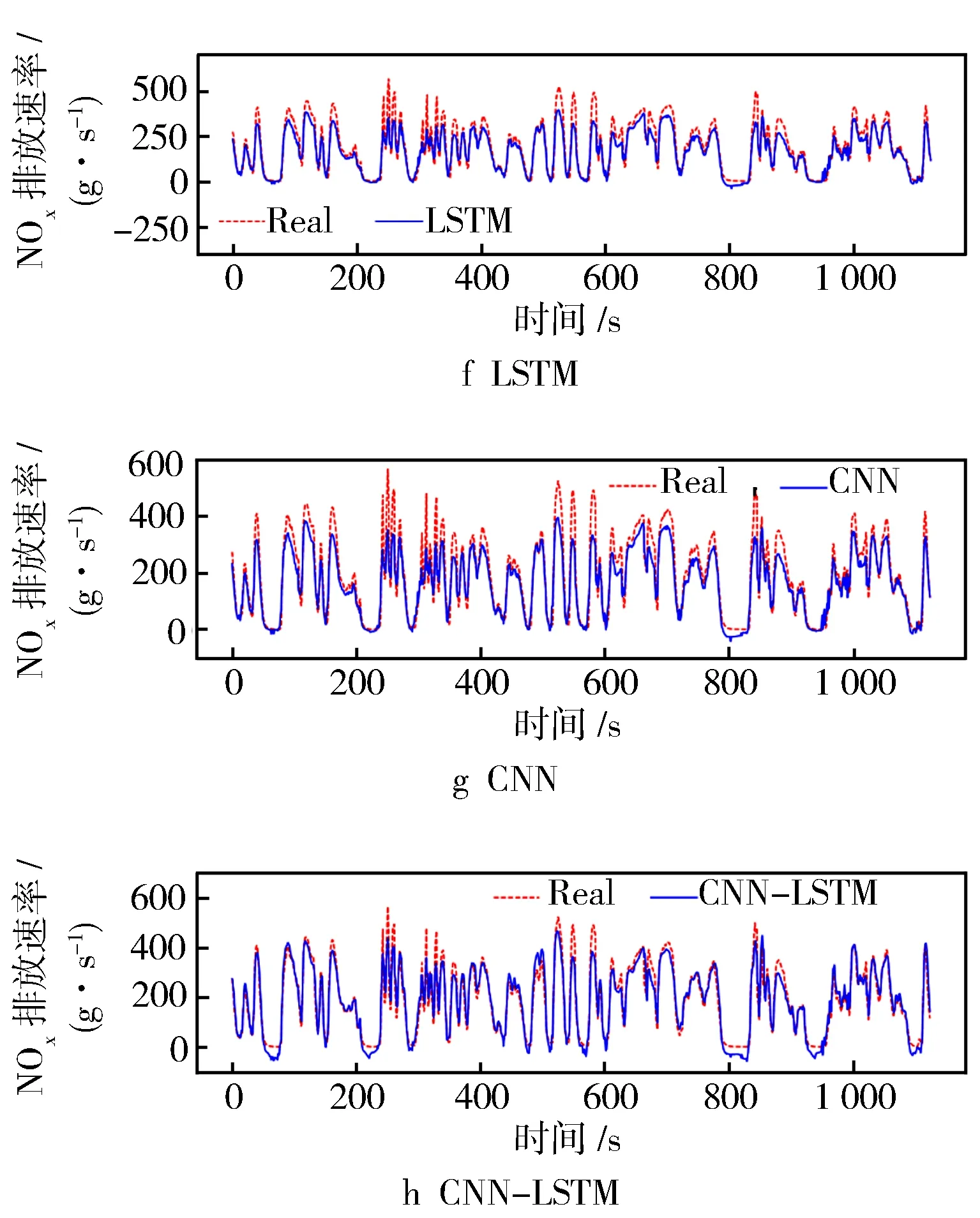
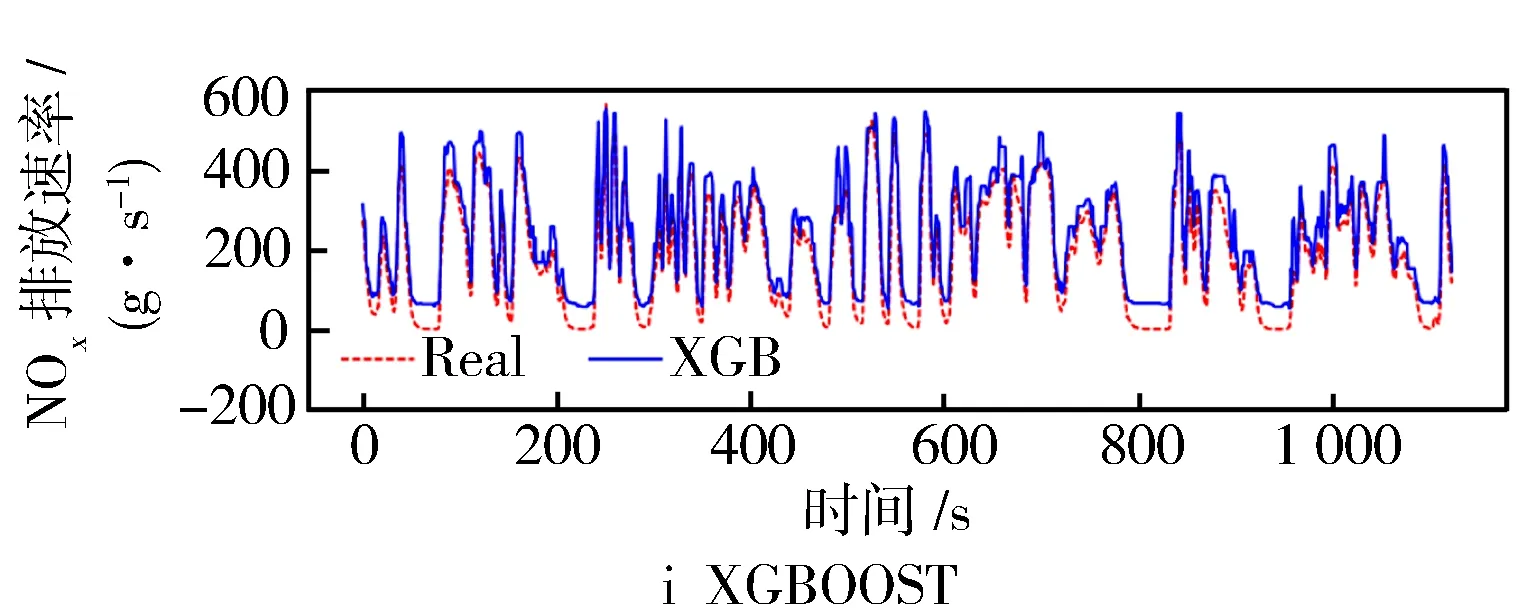
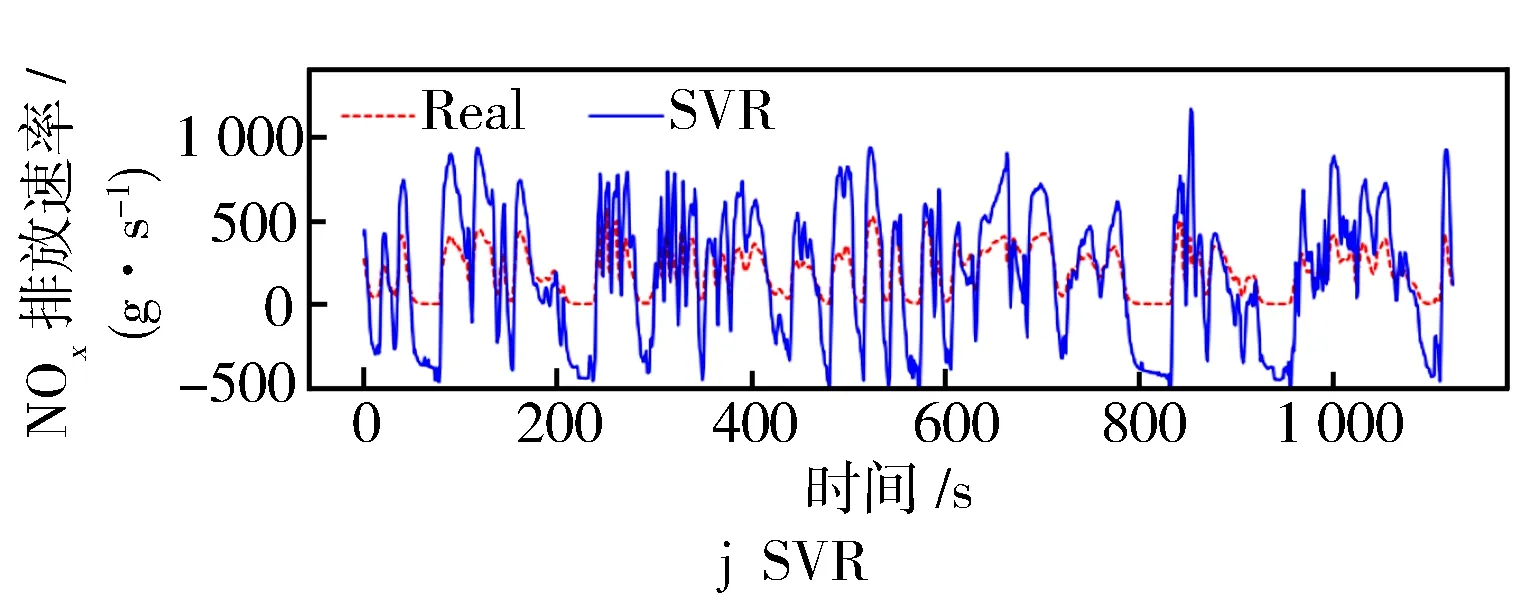
图8 排放预测模型预测结果对比

利用平均绝对比例误差MASE和均方根误差RMSE来衡量评判模型的性能。MASE值越低,模型性能越好;RMSE则用于衡量模型的预测准确性。引入R2系数来量化模型对未知样本数据的预测效果[25]。

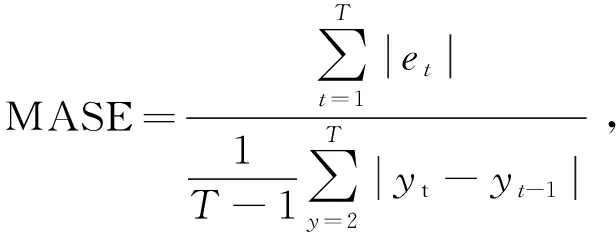
(13)

(14)

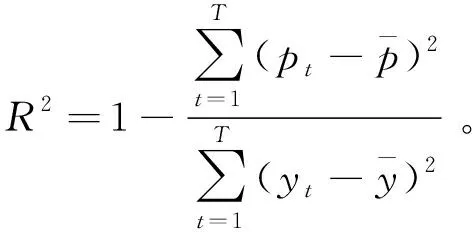
(15)

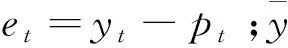
结合图8和表1中的数据可见,基于动态改进的遗传粒子群组合优化算法预测模型在R2指标上的表现为0.951,而在NOx排放预测整体误差方面,MASE为0.024,RMSE为0.033 6。值得注意的是,在排放峰值时刻(约在240 s和830 s)预测值与实际值存在偏差,这是由车辆运行条件变化以及模型对瞬态反应不足引起的。

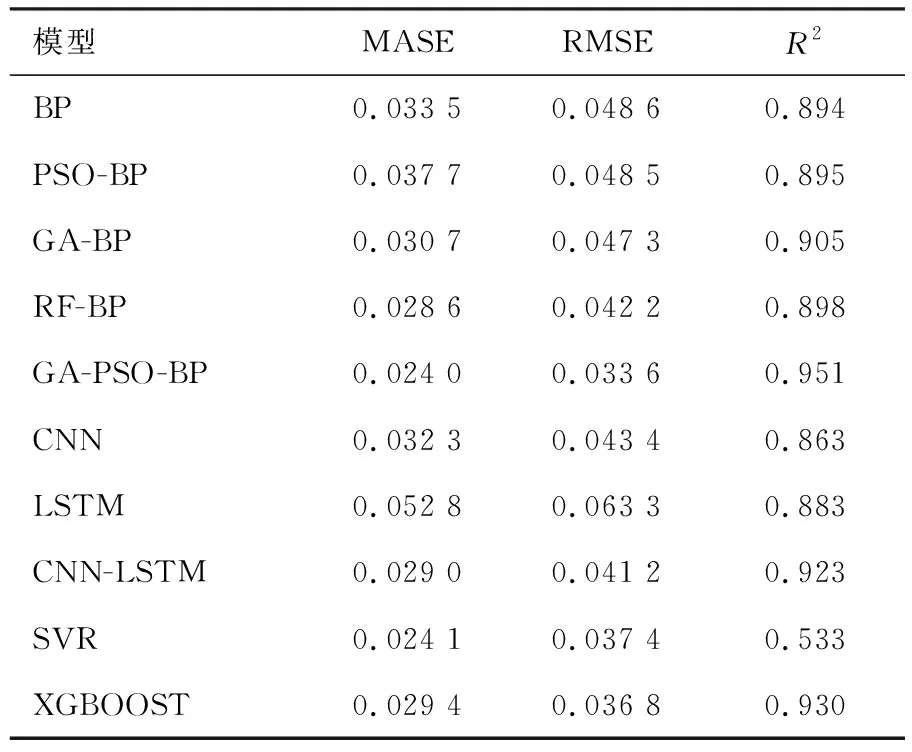
表1 模型预测结果的精度对比

从表2数据进一步分析可知,重型车行驶速度变化区间广泛,车速变化又与发动机状态密切相关,排放后处理设备反应时间受这些因素的影响,从而导致实际NOx排放速率波动。而从图7可见,NOx存在大量低排和少量高排的情况,这些数据导致预测模型在部分峰值结果和实际结果之间存在较大差异。需要指出的是,由于设备的原因,未考虑海拔等因素对排放的影响。在神经网络的训练过程中,模型参数的权重和阈值不断优化,主要目的是确定整体误差水平。

表2 重型车车速区间分布

通过变量相关分析和PCA分析,对数据进行特征提取,将原始变量缩减至11项主成分因子,从而降低了异常数据等对排放预测结果的影响。在NOx排放速率预测方面,基于动态改进的GA-PSO-BP组合算法展现出良好的准确性。预测值曲线的变化趋势与实际值的波动趋势相似,在R2、RMSE和MASE评价指标上表现优异,相较于其他预测模型有所提升。

4 结束语

在预测模型参数优化算法的选择上,动态改进的GA-PSO组合算法对比传统GA算法和PSO算法,在4个典型测试函数的性能验证上展现出良好的运行效率,有效弥补了各自算法的固有缺陷。

通过分析计算变量相关性,验证了变量之间存在有较强的耦合性和非线性特征,无法直接作为预测模型的输入;其中KMO检验结果为0.771,Bartlett’s球度P值为0.020 4,验证了样本适合于主成分分析;利用PCA特征筛选出了11个主成分因子,这些因子的累计贡献率达到99%,可以作为预测模型的输入。

通过建立其他预测模型并进行对比分析,使用R2、RMSE和MASE作为模型评价指标。结果表明,相较于其他预测模型,经过动态改进的GA-PSO组合算法BP神经网络在关键指标上有所提升,R2平均提升12.5%,MASE平均提升了20%,RMSE则平均提升了21.7%。动态改进后的预测模型在曲线拟合趋势和实际值的变化趋势方面表现出了良好的一致性。