基于平衡和非平衡权重算法的柴油机有机朗肯循环多目标优化

党玉荣,莫春兰,方颖聪,史科锐,张子杨,李作顺

(广西大学机械工程学院,广西 南宁 530004)

目前,柴油发动机燃料产生的能量只有40%左右被转化为有用功[1],大部分能量以热损失的形式被释放到环境中(如废气、夹套冷却水和润滑油等)[2]。其中柴油机废气的能量损失最大[3],所以高效回收废气余热对提高柴油机效率,实现节能减排具有重要的意义。有机朗肯循环(ORC)是进行余热回收、提高系统效率的有效方法[4]。

综上所述,目前对基于柴油机余热回收的非共沸混合工质ORC系统的多目标优化分析的研究较少,并且大部分研究对ORC系统的多目标优化都是基于平衡权重优化,对于非平衡权重优化缺少讨论。因此,本研究对非共沸混合工质ORC系统进行了非平衡权重和平衡权重的多目标优化分析,与传统的优化算法不同,本研究引入RPD-NSGA-Ⅱ(reference point dominance-based NSGA-Ⅱ)[16]算法进行多目标优化,该算法基于NSGA-Ⅱ进行改进,具有更好的解的多样性、更快的收敛速度以及更强的多目标优化能力,可处理ORC系统性能的复杂变化,最后通过TOPSIS(优劣解距离法)[7]进行综合分析,可为实际工程提供理论依据。

1 有机朗肯循环的模型分析

1.1 ORC系统描述

利用基于非共沸混合工质的有机朗肯循环对柴油发动机废气余热进行回收。以某直列6缸涡轮增压的柴油发动机为例[6],表1列出了发动机的主要参数。考虑发动机的废气温度较高,并且Ge等[17]研究表明非共沸混合工质(苯/甲苯)的输出功率高于相应的纯工质,所以系统选择了临界温度较高的苯和甲苯作为ORC的候选工质。工质的基本物性如表2所示[5,17]。图1示出了ORC系统的结构和温熵变化,整个热力过程为亚临界有机朗肯循环。首先,柴油发动机的废气在蒸发器与ORC的工质进行热交换,将工质加热成饱和蒸气(过程1—3),之后饱和蒸气在汽轮机膨胀做功(过程3—4),做功后的乏汽被冷凝器冷却成饱和液态(过程4—6),最后饱和液被泵加压后再次送到蒸发器(过程6—1)完成ORC循环。值得注意的是,由图1b可知基于非共沸混合工质的ORC系统的工质和和热源的匹配度更高。

图1 ORC系统的结构和温-熵图

表1 柴油发动机的主要参数[6]

表2 工质的基本物性[5,17]

1.2 有机朗肯循环的热力学模型

在MATLAB中建立了系统的热力学模型,利用REFPROP可以获得工质的热力学性质。为了简化ORC的热力学模型,提出了以下几个假设和条件:

1) ORC系统始终处于稳态运行状态,并忽略循环中的能量、摩擦和压力损失等;

2) 泵和涡轮的等熵效率分别为ηp=0.8和ηt=0.88;

3) 假设气液换热器夹点温度(Tpp,gl)和液液换热器夹点温度(Tpp,ll)分别为30 ℃和5 ℃;

4) 假设大气温度(T0)和压力(p0)分别为25 ℃和0.1 MPa;

5) 为避免酸腐蚀,蒸发器废气出口温度应不小于105 ℃;

6) 假设冷却水进口温度(Twi)为25 ℃,冷却水出口温度(Two)为35 ℃;

假设Tpp1=Tpp,gl,则ORC的质量流量(mORC)和蒸发器废气出口温度(Tgo)分别为

(1)

(2)

T2′′=T2+Tpp1。

(3)

式中:T2为蒸发温度;Cg为废气的比热容;h为流体的焓值。

假设Tpp2=Tpp,ll,则冷却水的质量流量(mw)为

(4)

(5)

Tpp2=T5-T5′′。

(6)

式中:Cw为冷却水的比热容。

1.2.1 能量模型

根据热力学第一定律,各设备的能量平衡方程列于表3。

表3 ORC系统组件的能量方程

系统输出功率(Wnet):

Wnet=Wt-Wp;

(7)

系统热效率(ηth):

(8)

柴油机废气能量(Qg):

Qg=Cg×mg(Tgi-T0);

(9)

柴油机废气能量回收率(ηg):

(10)

式中:Wt为汽轮机功率;Wp为工质泵功率;Qeva为蒸发器换热量。

表4 ORC系统设备的损方程

Izon=Ieva+Icon+It+Ip。

(11)

1.3 有机朗肯循环模型验证

为了保证仿真模型的准确性,采用了文献[18]中的ORC模型来确认计算的准确性。建立相同的边界条件:T3=88.86 ℃,T6=27.1 ℃,P2=PL=0.708 MPa,mORC=0.82 kg/s。如表5所示,模型与文献之间存在良好的一致性,最大误差为0.72%(小于5%),所以模型计算的数据是可靠的。

表5 ORC模型的对比结果

1.4 ORC系统的热力学性能分析

图2 ORC系统的热力学性能分析

2 基于热力学性能的多目标优化

2.1 RPD-NSGA-Ⅱ算法设计

RPD-NSGA-Ⅱ[16]基于传统NSGA-Ⅱ进行改进,在保持帕累托排序的同时强调了收敛性和多样性。为了验证RPD-NSGA-Ⅱ算法的优越性,通过引入多目标优化评价指标IGD(反转世代距离)可以评价算法的收敛性和多样性[19],而IGD值越小对应的算法性能越优异。

2.2 目标函数和决策变量

表6 决策变量的变化范围

max(Wnet)=f1(T2,mf),

(12)

max(ηth)=f2(T2,mf),

(13)

min(Izon)=f3(T2,mf)。

(14)

2.3 多目标优化决策

经过优化算法得到的Pareto解集都是目标的最优解,需要根据不同目标函数的权重进行归一化后选出最满意的解。而TOPSIS可以利用数据的差异来进行决策和分析数据之间的差距,并确定最佳的运行参数[7]。具体计算如下:

优化解集与理想点之间的空间距离可计算为

(15)

从优化解集到非理想点的距离被定义为

(16)

评价样本与最优解之间的接近程度可以表示为

(17)

式中:Fjideal和Fjnon-ideal分别为理想解和非理想解。

基于上述热力学和优化模型,制定了如图3所示的ORC的详细设计和优化流程。

图3 ORC的计算流程

2.4 优化结果分析

通过platemo平台[20]利用RPD-NSGA-Ⅱ算法对ORC系统的热力学性能进行多目标优化。表7对比了PSO算法[11]和NSGA-Ⅱ算法[15],以及基于NSGA-Ⅱ算法改进的NSGA-Ⅱ-SDR(strengthened dominance relation)算法[21]和RPD-NSGA-Ⅱ算法[16]。结果表明:RPD-NSGA-Ⅱ算法的IGD值和与真实数量的误差都最小,所以该算法的性能最好。值得注意的是,虽然NSGA-Ⅱ-SDR也对NSGA-Ⅱ算法进行了改进,但IGD值和误差明显高于NSGA-Ⅱ算法,这说明虽然经过算法改进,但是对于ORC系统的性能优化并不适用。最后经过RPD-NSGA-Ⅱ算法得到帕累托前沿,然后通过TOPSIS可从Pareto前沿中选取热力性能的综合最优解。

表7 优化算法的评价指标比较

图4示出了通过高维多目标优化(EMO)和TOPSIS选择的ORC系统热力学多目标优化过程。由图可知,第一次迭代的初始种群分布比较密集,等迭代次数分别达到50次和100次,可以发现种群多样性和收敛性明显得到优化。Izon与Wnet呈正相关,而ηth与Wnet和Izon呈负相关。表8列出了基于高维EMO和TOPSIS选择的热力学结果。基于平衡ηth,Wnet和Izon的TOPSIS选择方法,最佳ηth,Wnet和Izon分别为24.07%,72.36 kW和44.66 kW,结合式(9)和式(10)可知此时柴油机废气能量回收率为12.5%。若基于平衡Wnet和ηth选择,则Wnet增加了12.22%,而ηth却减少6.56%,相应地Izon增加了16.61%。若基于平衡Wnet和Izon选择,则Wnet和Izon分别增加0.21%和0.76%,相应地ηth减少0.37%。值得注意的是,若基于平衡ηth和Izon选择,ηth增加了10.72%,而Izon减少了83.61%,相应地Wnet减少了86.01%。因此,对ORC热力学的分析表明,减少Izon势必会使ηth增加、Wnet降低,无法获得同时满足三个性能指标的参数,但基于不同权重的分析可以给出实际工程更多选择。

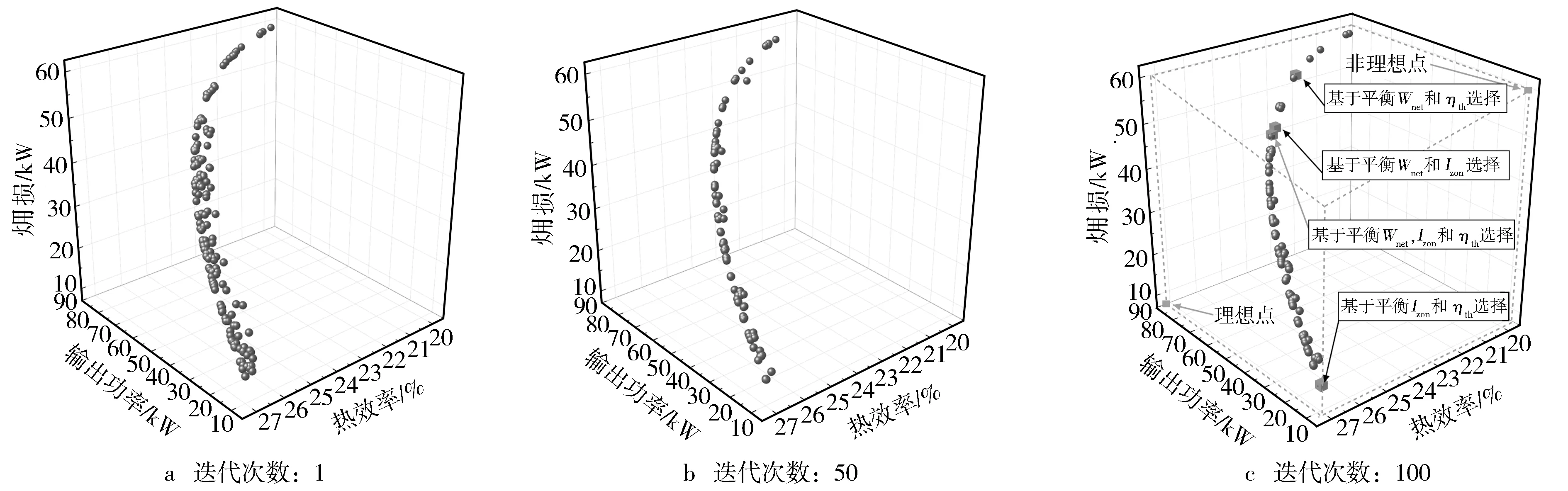
图4 基于高维EMO平衡权重的ORC系统热力学分析

表8 基于高维EMO平衡权重和TOPSIS选择的热力学参数

图5示出了基于不同评价指标的非平衡权重分析情况。由图5a可见,Wnet和ηth的非平衡权重关系呈负相关。这说明Wnet高时ηth不理想,而ηth高时Wnet不高,可认为ηth和Wnet之间是支配性关系。由图5b可见,基于ηth和Izon的非平衡权重关系呈负相关,因此,优化ηth总能减少Izon,而Izon的减少也能增加ηth,ηth和Izon之间是支配性的关系。由图5c可见,基于Wnet和Izon的非平衡权重关系呈正相关,因此,优化Wnet和优化Izon是相互矛盾的,Wnet的提高是以增加Izon为代价的,而Izon的减少是以减少Wnet为代价的,所以Wnet和Izon之间是非支配性的关系。

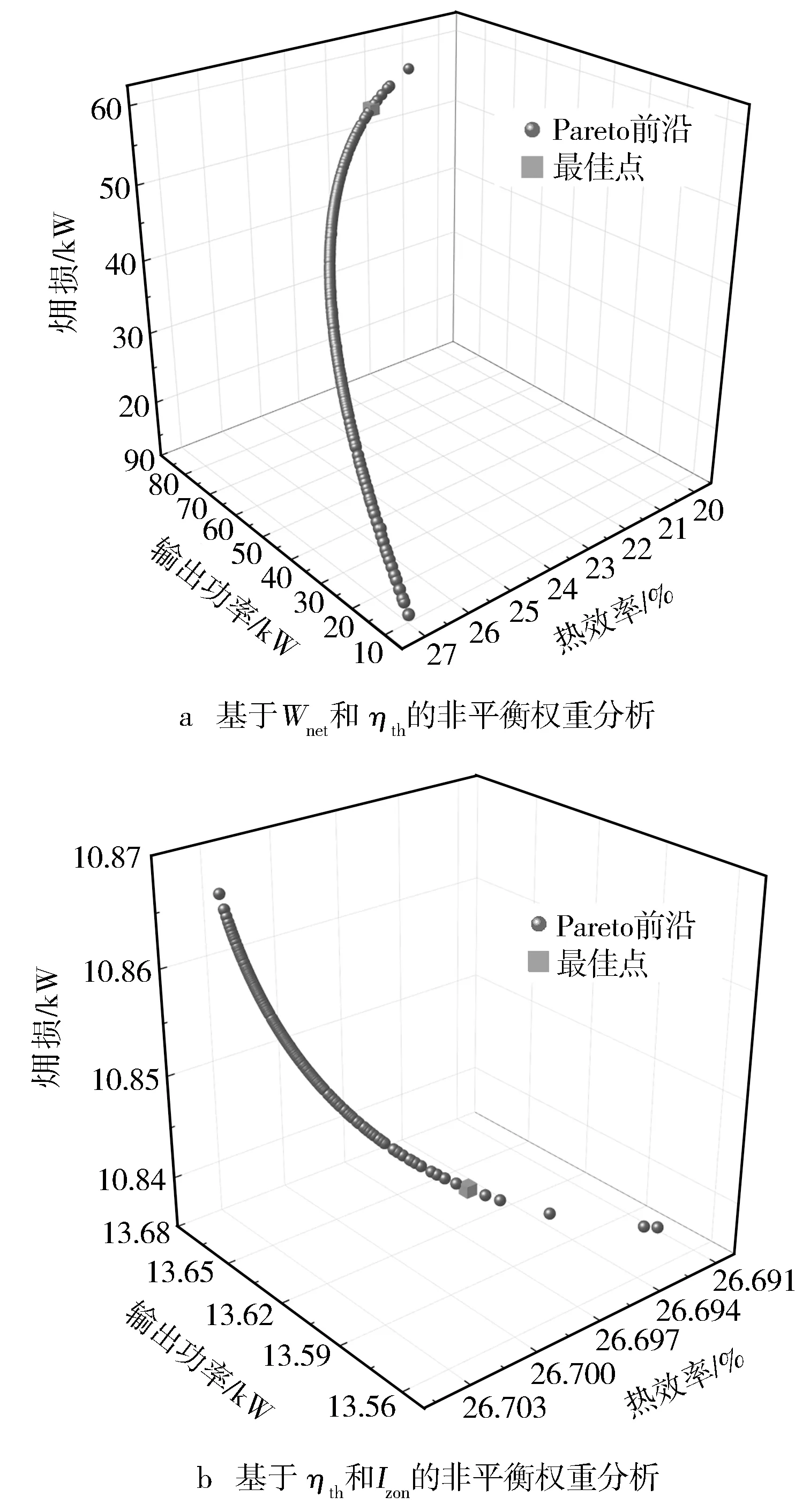
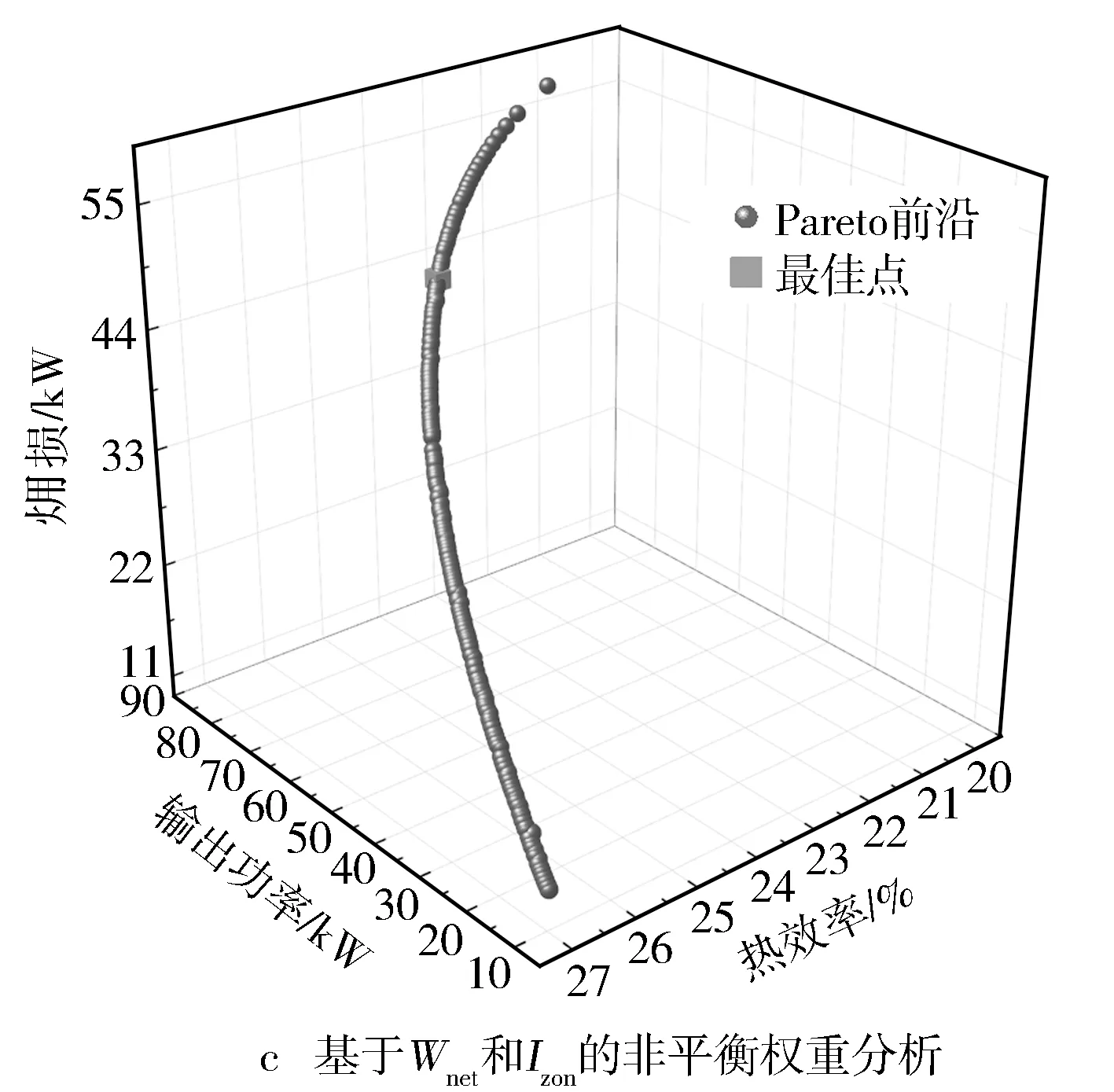
图5 基于不同评价指标的非平衡权重的ORC系统热力学分析

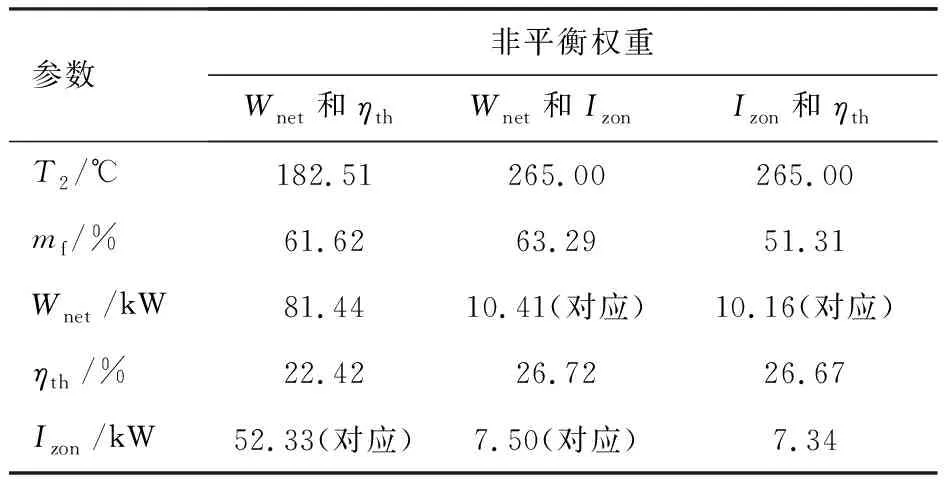
表9 基于不同评价指标的非平衡权重的热力学性能

表10 基于单一评价指标的热力学参数

3 结论