脉冲来流下蜗壳几何参数对涡轮流动特性的影响

黄磊, 赵荣超,诸葛伟林,丁占铭,张扬军

(1.华南理工大学机械与汽车工程学院,广东 广州 510641;2.清华大学汽车安全与节能国家重点实验室,北京 100084;3.中国北方发动机研究所柴油机增压技术重点实验室,天津 300406)

在涡轮增压内燃机中,涡轮通过回收排气能量用于增压,使内燃机功率密度与燃油经济性显著提高。蜗壳的作用是将内燃机排气导向转子,其设计对涡轮效率具有重要影响[1-5]。在蜗壳设计中,蜗壳的A/R值对转子进口入射角具有决定性影响,通过合理设置A/R值可获得最优效率。此外,蜗壳截面形状对涡轮的内部流动损失有重要影响。曹刚等[1]基于数值模拟方法研究了4种不同形式蜗壳流道对涡轮机性能的影响,发现梨形截面流道的效果最佳。吴娜等[2]以螺旋贝壳为仿生原型,通过数据优化得到蜗壳仿生设计截面曲线,减少了蜗壳壁面流动损失,使涡轮效率提高3%～5%。Wei等[4]建立了发动机与涡轮的耦合模型,定量对比了单通道蜗壳和双通道蜗壳设计对发动机性能的影响,结果表明双通道蜗壳使发动机输出功率提高2.3%。以上研究主要关注蜗壳主要设计参数,较少考虑蜗壳细节设计参数对转子进口流动畸变的影响。

此外,传统的蜗壳设计与性能评价主要基于稳态来流条件,而实际上,由于内燃机排气门周期性启闭,涡轮进口为脉冲流动,即气流的压力、温度、流量等参数均周期性变化,蜗壳出口流动角也大幅度偏离设计值,导致涡轮效率的显著下降[6-7]。Karamanis等[8]最早通过激光多普勒速度测量仪观察转子进、出口速度变化,发现脉冲周期内涡轮转子进口相对气流角在-83°～52°内变化,出口相对气流偏离角在-17°～26°内变化,导致涡轮循环平均效率下降4%～25%。Palfreyman[9]采用数值模拟方法对同一涡轮的脉冲流动开展研究,发现转子横截面上的速度分布是高度畸变的,在脉冲波峰时刻,叶片吸力面出现了较强的分离涡和叶尖泄漏涡,是涡轮流动损失的重要来源。Yang等[10]研究了脉冲来流下蜗壳截面形状对蜗壳内部流动损失及下游转子的影响,指出扁平型截面由于转角尖锐导致蜗壳内二次流损失增强,转子进口流动畸变增强致效率较低。国内外学者进一步研究了脉冲特征对涡轮特性的影响。Padzillah[11]基于数值模拟方法,发现脉冲频率对转子进口攻角的分布具有显著影响,当脉冲频率较低时,转子进口攻角周向分布较为均匀,当脉冲频率提高后,进口攻角的周向不均匀程度加剧。王智慧等[12]发现脉冲频率对低压侧转子进口入射角影响更大,脉冲频率越低,低压侧的转子进口负入射角越大。刘尹红等[13]基于数值模拟方法,发现导流叶片泄漏流量和总压损失及激波随脉冲进口压力提高而线性增大。赵荣超等[14]研究了脉冲频率和幅度对两级涡轮特性的影响,发现随脉冲频率提高,高压级涡轮平均效率下降,而低压级涡轮效率变化不大,但脉冲幅度对低压级涡轮效率的影响显著。

由于蜗壳设计参数与转子进口攻角变化密切相关,而脉冲来流又影响了转子进口攻角的周期性变化,脉冲来流与蜗壳设计的时空耦合关系对涡轮效率具有显著影响,目前蜗壳设计如何影响气流角在周向和叶高方向的变化缺乏系统全面的研究,尤其是蜗壳细节设计参数的影响缺乏研究。本研究基于三维非定常数值模拟方法,研究了脉冲来流下蜗壳出口半径、蜗壳截面形状、进口导管角等几何对涡轮流动特性的影响,以期为脉冲来流下的蜗壳细节气动设计提供参考。

1 数值仿真模型

1.1 数值模拟方法

本研究的涡轮应用于某柴油机的电动涡轮复合系统,该涡轮包含蜗壳和叶轮两个主要部件。基于ANSYS CFX平台开展涡轮内部流动的数值模拟研究,涡轮级的网格划分如图1 所示,蜗壳内流道采用非结构网格,叶轮通道内的网格采用结构化网格,两个部件的网格离散分别在ANSYS ICEM和TurboGrid中完成。蜗壳中约包含86万网格单元,涡轮转子通道约含307万网格单元(全通道),总网格数量约为393万,蜗壳与转子交界处的流动信息交换采用冻结转子法处理。采用SST湍流模型进行求解,壁面设置为无滑移绝热边界条件。

根据发动机标定工况点下的涡轮进口参数给定计算边界条件,进口边界条件给定为周期性变化的总压和总温(见图2),脉冲周期内的进口平均总压为285 kPa,平均总温为930 K,出口边界设置为恒定静压。

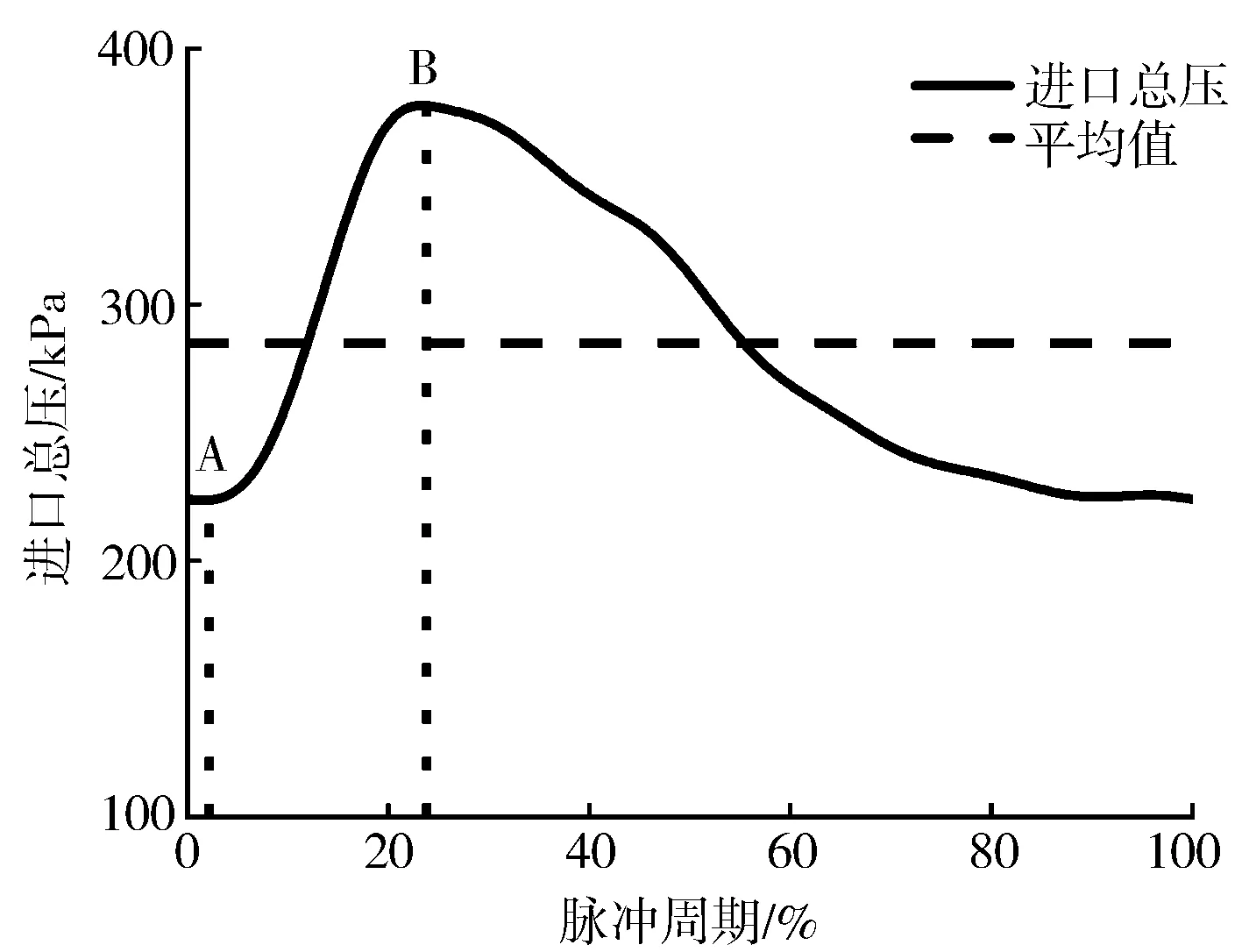
图2 进口压力边界条件

对数值模型开展网格无关性验证,采用不同网格数量对蜗壳进行离散,观察网格单元数量对计算结果的影响,预测得到的瞬态扭矩如图3所示。对涡轮轴峰值扭矩进行归一化(见表1),当网格数量大于53万后,网格数量对瞬态扭矩的预测结果影响较小,涡轮轴峰值扭矩的变化不超过0.3%,在兼顾计算效率和精度的前提下,后续研究中蜗壳网格数量控制在100万以内。

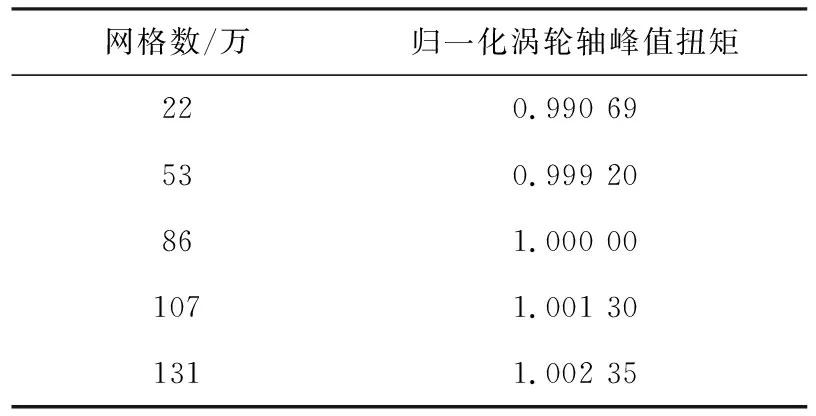
表1 涡轮轴峰值扭矩

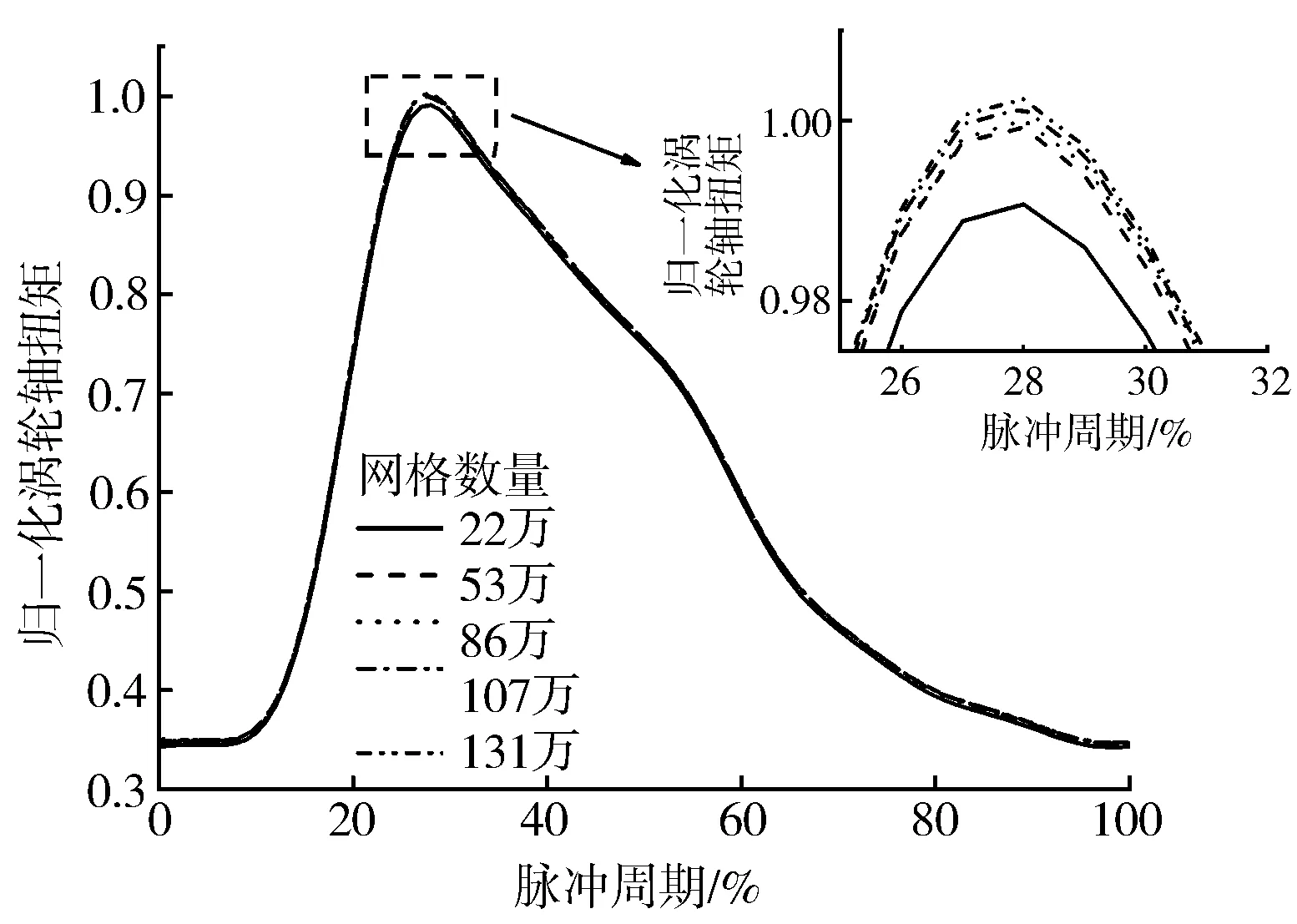
图3 网格无关性分析

为验证本数值模拟方法的可靠性与精确度,以参考文献[15]中的高压级涡轮为研究对象,将数值模拟计算结果与试验结果进行比较,脉冲周期内的涡轮瞬态扭矩对比如图4所示,涡轮瞬态峰值扭矩预测值与试验值偏差为4.25%,因此本研究建立的数值模拟方法是可靠的。

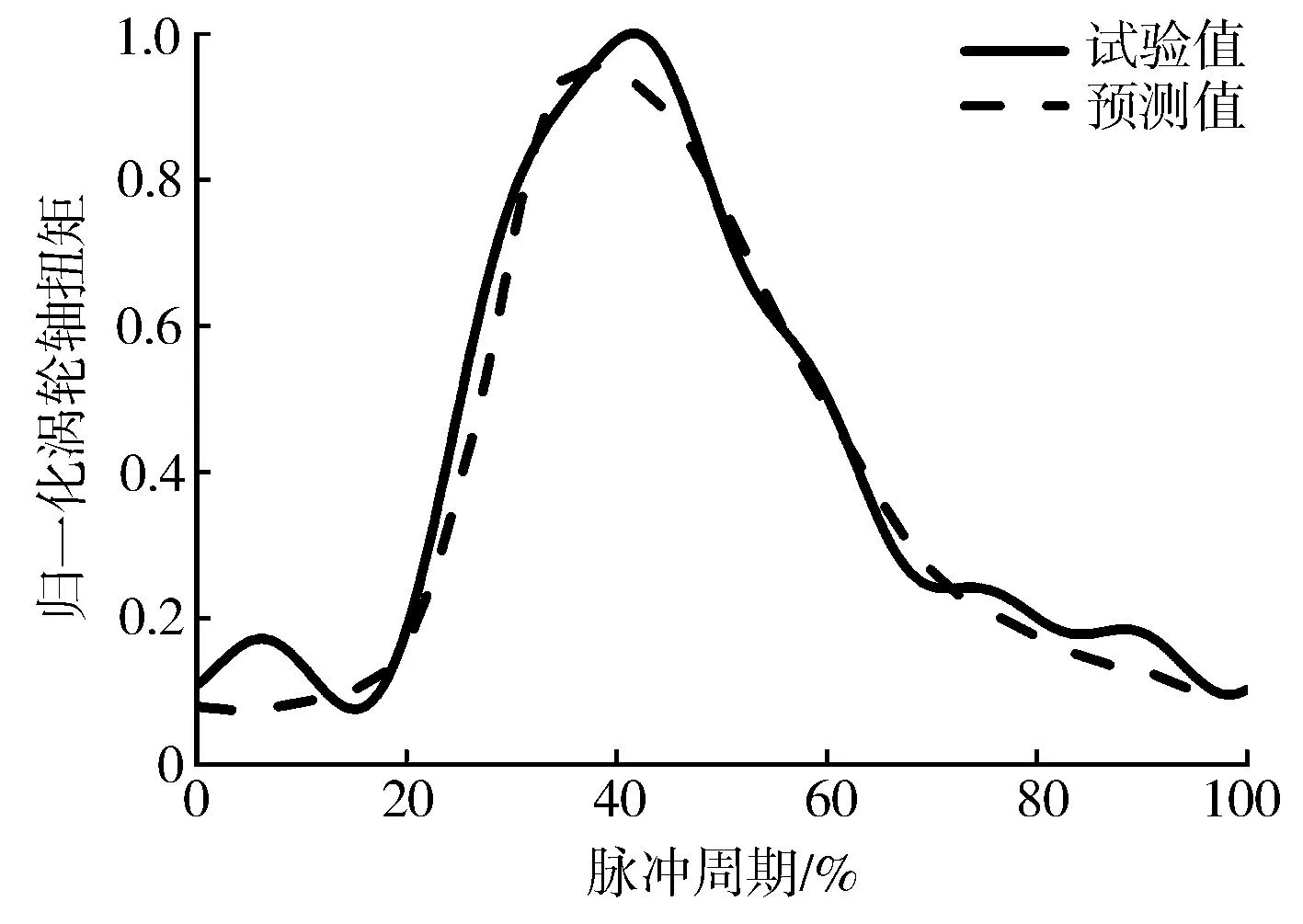
图4 脉冲来流下涡轮性能试验值与数值模拟结果比较

1.2 蜗壳设计方案

针对蜗壳出口半径、截面形状和进口导管角开展设计研究,研究方案如图5所示。R1和R2分别为蜗壳出口半径和叶轮进口半径,R1/R2分别取1.062,1.108和1.154三个方案,在三种方案中,R2保持不变,只调整R1。蜗壳出口半径影响了蜗壳出口与叶轮进口之间过渡段的长度,蜗壳出口半径越大过渡段越长。由于蜗壳几何的非轴对称性,转子进口流动在周向方向上是不均匀的,通过增加过渡段长度可减弱转子进口的周向非均匀性,因此开展了不同蜗壳进口半径的影响研究。蜗壳截面形状包含了近圆形方案、梨形1.3和梨形2.0三个方案。在梨形方案中,侧面型线为直线段,长度记为a,与竖直方向的夹角为25°,顶部为贝塞尔曲线,贝塞尔曲线控制点与直线段下端点的距离为b,在梨形1.3和2.0方案中,b/a分别取1.3和2.0。在理想情况下,蜗壳进口导管引导气流切向进入,其角度应为0°,在实际设计中,蜗壳末端与进口导管可能会出现干涉现象,为了避免干涉,进口导管向外倾斜一定角度γ,本研究进行了外倾角分别为5°,10°和15°时涡轮的气动特性研究。在以上方案中,蜗壳喉口处的截面积保持一致。

图5 蜗壳几何参数示意

脉冲来流下涡轮的瞬时效率和时均效率分别如式(1)和式(2)所示,涡轮流量特性参数MFP的瞬态值和平均值的计算分别如式(3)和式(4)所示。

(1)

(2)

(3)

(4)

在脉冲来流中,由于进口参数的时变特征,采用熵参数描述涡轮内部流动损失将与实际情况产生较大偏差。在本研究中,采用熵产率[16]描述由于黏性力引起的当地流动损失,其定义如式(5)所示。熵产率表征了单位体积内由于黏性流动所产生的流动损失,与局部速度梯度相关,局部速度梯度越大,由于黏性力引起的流动损失越大。

(5)

2 结果分析

2.1 蜗壳出口半径的影响

转子进口绝对气流角的分布如图6所示,在周向和叶高方向上均表现出较强的不均匀性,而不同脉冲时刻下绝对气流角的变化不大。

图6 蜗壳出口半径对转子进口气流角时空变化的影响

在蜗舌位置(0°或360°)前后,气流角发生较大变化。经过蜗壳喉口前气流角急剧增加,最高约达85°,经过喉口后,流动角则迅速减小,由此可见,蜗壳喉口的存在导致较强的流动周向畸变。从图中还可以看出,蜗壳出口半径对周向畸变具有显著影响,蜗壳出口半径减小,周向畸变显著增强。在R1/R2=1.062方案中,0°附近的最小气流角仅约为52°(50%叶高),而在R1/R2=1.154方案中,0°附近的气流角并未出现大幅度下降,气流角在周向上的分布较为均匀。

此外,当出口半径过小时,叶高方向的不均匀性也大幅度增强,在R1/R2=1.062方案中,10%和90%叶高处的气流角显著低于50%叶高处的气流角。其原因主要是当流体从面积较大的蜗壳截面进入转子时,两侧流体向中心聚拢,造成叶高方向的流动不均匀,当蜗壳出口半径增加后,蜗壳与转子间过渡长度增加,流体经较长距离混合后再进入转子,流动均匀性提高。

图7示出了蜗壳对称面上的马赫数分布。在R1/R2=1.062方案中,第1个叶片通道(0°～30°)进口马赫数较低,主要原因在于从蜗壳进口导管流出的流体经过喉口截面后面积发生突扩,致使该位置流动速度下降;在第12个叶片通道(330°～360°)进口,马赫数则显著增加,主要原因在于该处为蜗壳末端,由于蜗舌的存在,该处面积收缩较为突然,致使速度显著增加。与之对比,在R1/R2=1.154方案中,马赫数的周向分布较为均匀,第1个叶片通道与第12个叶片通道进口的马赫数差异不大,主要原因在于蜗壳末端的流体经过蜗舌后重新补充到第1个转子通道中,避免了第1个转子通道中流体速度过低。

图7 蜗壳对称截面的马赫数云图

蜗舌附近的流动和熵产率如图8所示。在R1/R2=1.062方案中,蜗壳末端的少量气流经过0°位置后进入转子,该部分气流与进口导管气流在该处附近交汇,在15°位置,蜗壳出口处可见较强的熵产损失。在R1/R2=1.154方案中,蜗壳末端仍有较多气体流经0°位置,在30°位置前全部进入转子,即第一个叶片通道的气流主要由蜗壳末端气流提供,减弱了蜗舌对该位置的流动不均匀性的影响。

图8 蜗壳出口半径对蜗舌附近熵产率的影响(时刻B)

以下分析脉冲时刻A和时刻B下转子内部流动损失,时刻A和时刻B标注见图2。转子通道中的熵产损失如图9所示,在脉冲时刻A,由于进口负攻角导致叶片压力面产生较为显著的熵产损失,在蜗舌的影响下,R1/R2=1.062方案中0°对应的叶片两侧均产生显著损失;在脉冲时刻B,由于进口攻角较大,在叶片吸力面产生较大的熵产损失,由蜗舌导致的周向进口气流角和速度的畸变,致使0°附近损失显著大于其他叶片通道。通过增大蜗壳出口半径,周向和叶高方向的流动畸变得到有效抑制,脉冲时刻A和时刻B时,R1/R2=1.154方案中叶片压力面和吸力面产生的熵产损失均显著减小,同时周向熵产率分布更加均匀。

图9 蜗壳出口半径对转子50%叶高熵产率的影响

蜗壳出口半径对脉冲周期内涡轮平均效率和MFP的影响如图10所示,R1/R2=1.154时获得最高效率,与R1/R2=1.062方案相比,效率提高约4.1%,MFP降低约5.6%。

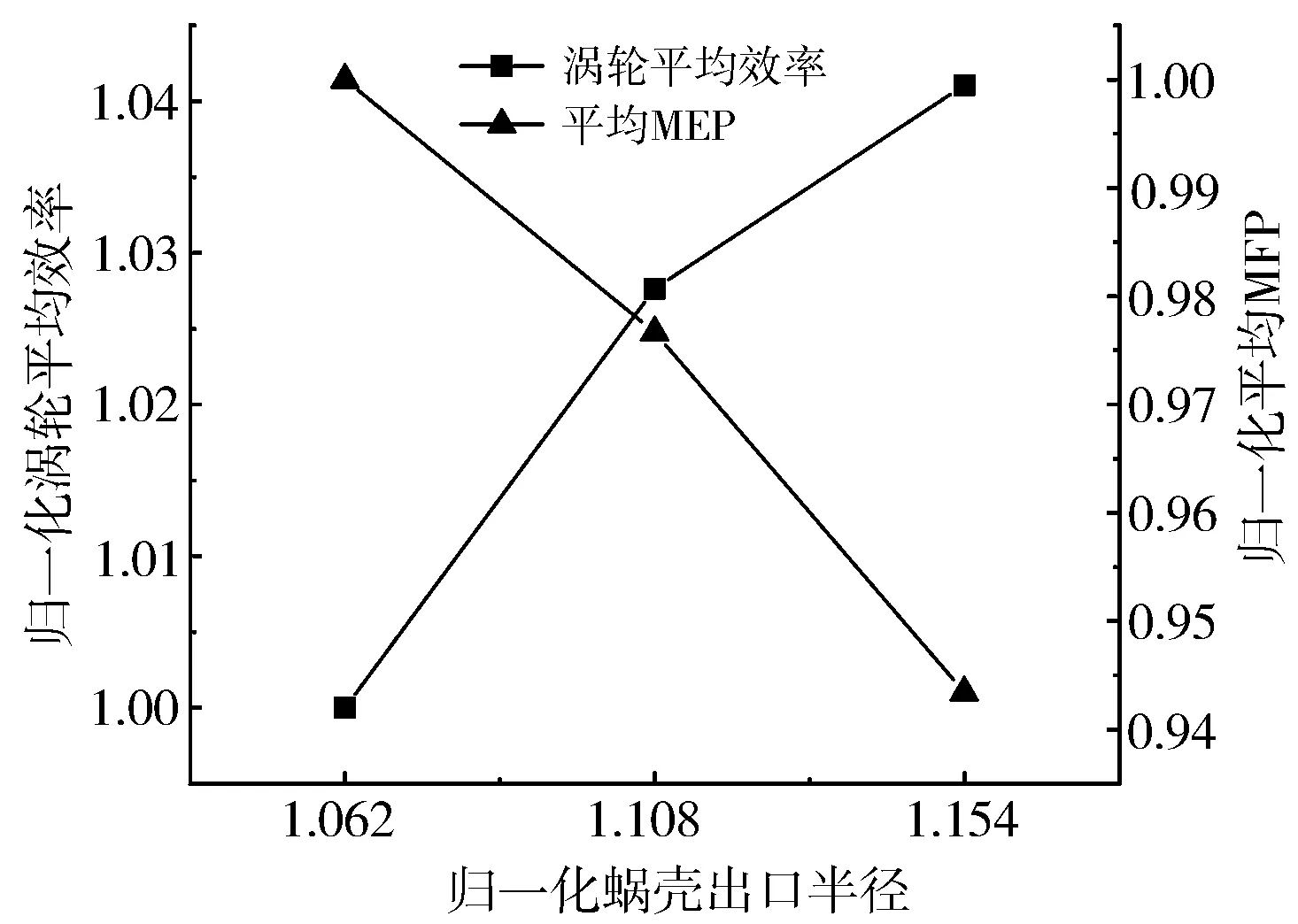
图10 蜗壳出口半径对平均效率和MFP的影响

2.2 蜗壳截面形状的影响

在本节的三个研究方案中,蜗壳出口尺寸采用R1/R2=1.154,喉口面积保持一致。计算结果表明,截面设计对速度分布影响较小(见图11)。三种方案的进口气流角在蜗舌位置均发生一定程度的降低,但并不显著。此外,圆形方案中转子进口气流角要小于梨形方案,主要原因在于圆形截面的形心更靠近转子中心,因此其等效A/R值比梨形方案要大,导致其气流角略小于其他两种方案。

图11 蜗壳截面形状对转子进口气流角时空变化的影响

三种设计方案下蜗舌附近的流动和熵产率如图12所示。喉口截面(0°)底部产生的较强的熵产损失在梨形2.0方案中最为显著,主要原因在于进口导管截面形状从进口截面的圆形过渡到喉口处的梨形,导管下半部分流体经历收缩加速过程,流体速度梯度的增大引起熵产率增加。而在15°截面上,圆形方案中的熵产率则要显著大于另外两种方案,其原因在于来自导管的流体速度较低,而从蜗壳末端重新流入的流体速度较高,两股流体在掺混过程中产生较显著的熵产损失;此外,流体从圆形截面进入到转子通道的过程中,流通面积变化率大也导致熵产率的增加。

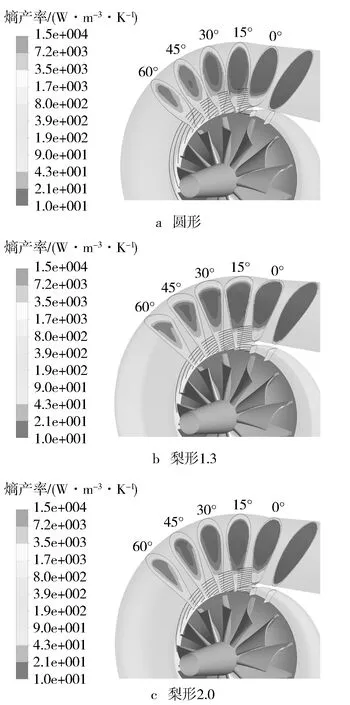
图12 蜗壳截面形状对蜗舌附近熵产率的影响(时刻B)

蜗壳截面对脉冲来流下的涡轮平均效率和MFP的影响如图13所示。梨形1.3方案的效率最高,与圆形方案相比约高1.3%,梨形1.3和梨形2.0方案之间的差异较小;梨形方案的MFP略小于圆形方案,梨形1.3的MFP比圆形方案低约3.0%。

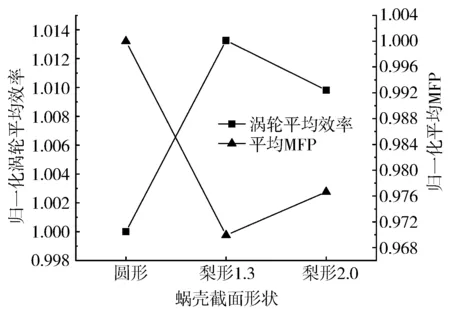
图13 蜗壳截面形状对平均效率和MFP的影响

2.3 蜗壳进口导管角的影响

进口导管角对转子进口气流角分布的影响见图14。在远离蜗舌的位置,不同导管角下的气流角几乎一致,几乎不受导管角影响。不同方案之间的差异主要体现在蜗舌附近,当进口导管角为15°时,蜗舌附近的绝对气流角显著减小,周向畸变增强。主要原因可能在于导管外拐后,气流并非切向进入蜗壳,速度的切向分量有所减小,导致0°～30°周向位置进口气流角显著减小。远离蜗壳喉口后,气流角主要受蜗壳截面积变化规律影响,受导管角影响较小,因此不同方案下的气流角分布差异不大。

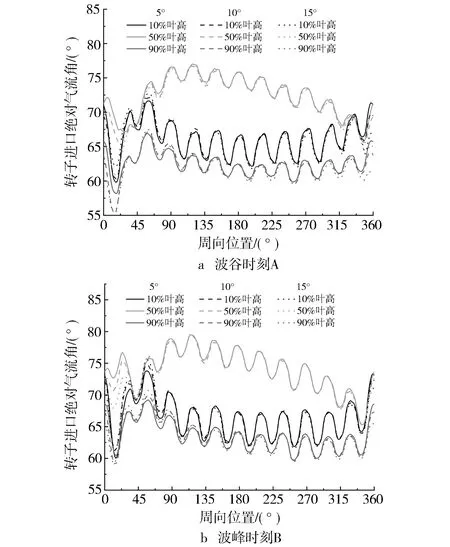
图14 蜗壳进口导管角对转子进口气流角时空变化的影响

转子内部熵产率损失如图15所示。在脉冲时刻A,进口气流负攻角导致叶片压力面前缘产生较显著的熵产损失,在蜗舌位置,15°方案的气流负攻角更大,因此产生了更为显著的熵产损失。在脉冲时刻B,较大的气流正攻角导致叶片吸力面产生了大范围的熵产损失,在蜗舌位置,15°方案的气流正攻角减小,因此该处的熵产损失减小。

图15 蜗壳进口导管角对转子50%叶高熵产率的影响

进口导管角对涡轮平均效率和MFP的影响如图16所示。随进口导管角增加,效率小幅度下降而MFP略微增加,效率下降约0.87%,MFP增加幅度约为2%。可以推测,进口导管角增加后,进口气流切线与转子中心的距离减小,导致喉口处实际半径减小,即蜗壳A/R值增大,因此MFP随蜗壳进口导管角的增大而小幅度增加。

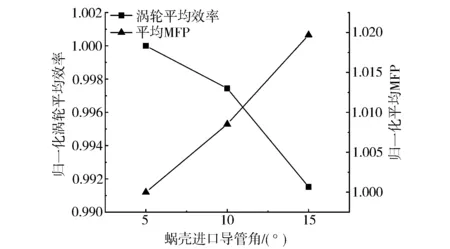
图16 蜗壳进口导管角度对平均效率和MFP的影响

3 结论

a) 当R1/R2从1.062增加到1.154时,蜗壳末端气流有效抑制蜗舌引起的周向畸变,脉冲来流下涡轮平均效率提高约4.1%;当蜗壳出口半径较小时(R1/R2=1.062),转子进口马赫数和流动角在0°位置前后先急剧增大后减小,周向方向上的速度畸变导致流动损失的显著增加;在脉冲波峰时刻,0°位置叶片吸力面熵产率显著增加,而在波谷时,该处压力面熵产率显著增加;

b) 蜗壳截面采用梨形1.3方案略优于梨形2.0方案和圆形方案,梨形1.3方案的涡轮平均效率比圆形方案提高约1.4%;圆形方案中,由于末端高速气流与进气导管低速气流混合,在蜗舌下游15°处可观察到较显著的熵产损失;

c) 涡轮效率随进口导管角的增大而下降,进口导管角主要影响蜗舌附近的气体流动,对其他相位角的流动几无影响;导管角增大后,喉口处切向速度分量降低,引起0°位置附近气流角的显著下降;脉冲波峰时,0°叶片吸力面熵产率降低;脉冲波谷时,该处叶片压力面熵产率增加;导管角从5°增加到15°后,涡轮平均效率下降约0.9%,MFP增加幅度约为2%。