基于核心素养导向的高中数学教学研究与实践
孙雷鸣
【摘要】“借助计算器观察函数递增的快慢”是上海普通高中数学教材《幂函数、指数函数和对数函数》章节的选修内容.在高一数学教材中,该节内容处在“指数函数”之后.在此之前,学生已经较为系统地学过线性函数、幂函数和指数函数等.文章深入剖析本课题教学内容,引入平均变化率,以问题驱动的形式让学生理解其意义.本课题的教学目的在于引导学生掌握研究问题的方法:“观察—归纳—猜想—证明”,进一步提高学生的数学探究能力、数学建模能力和数形结合的能力.
【关键词】数学核心素养;平均变化率;数形结合
一、教学内容分析
在前一节中,“银行的利息”和“人口的增长”两道例题让学生充分地体会到指数函数的“爆炸性”增长速度.试想当线性函数、幂函数和指数函数都为增函数时,指数函数为什么具有更为显著的“爆炸性”增长的特点?从数学的角度如何刻画和描述这个增长变化特征,就是本节课内容的基本出发点.
在研究函数递增快慢的过程中,引入平均变化率的概念,用数值进行比较,提供了分析函数增长快慢的数学模型.平均变化率是函数单调性的拓展和延伸,为今后研究导数的概念奠定了基础.
本节课授课的学生是高一新生,对计算器的使用不是很熟练,在本节课中将学习如何使用计算器的列表功能.目前,学生已基本掌握了幂函数、指数函数的一些基本性质,通过探究一些具体函数递增的快慢,能让学生对这些函数的性质有更深入的了解.
二、学情分析
作为高中数学教师,更应关注发展学生的数学学科核心素养,数学教学该怎么做?如何在课堂上有效地发展学生的数学学科核心素养?实践表明,教学研究是理念转化为实践的有效媒介,可以为教师提供理论与实践相结合的载体,为教师的教学实践提供有效的抓手.笔者聚焦于将学科核心素养转化为可操作的教学目标,明确教学方向;通过具体的课堂教学研究,落实培养学生数学学科核心素养,改进教学,立德树人.
本篇以“借助计算器观察函数递增的快慢”为例,开展以素养为导向的教学研究.本篇主要聚焦以下几点:
1.用数学问题引领实践创新———用数学问题开展自我导向的学习,课堂上我们有学习任务单,学生可以按照计划形成学习成果,并有自我评估意识.学生在不断提问和思考中,形成数学思维,在主动借鉴中取长补短,共同发展.
2.用学科核心素养让学生学会学习———让学生学会高阶思维,能够从现象中看到本质,提高学生动手实践能力.学生能够基于函数图像归纳和猜测结论,最终能够进行缜密的逻辑推理并得出結论.在探究过程中,学生能自己总结概念,且能对他人的观点进行质疑、批判,形成自己的解释并给出理论证明.
3.用小组协作相互启发评价———以小组形式共同完成任务单和课堂反思.课堂上,学生通过小组合作,完成计算器的操作和证明方法的选取,共同研究探讨.课后,完成任务单的课堂反思,实现自主评价,不断反思总结.
4.用计算器工具增强信息意识———体会信息技术的利弊.在本节课中,有些问题是可以使用计算器得到数据,再根据数据去猜测,学生可以体会信息技术带来的优势,同时需要严谨的代数证明,本节课学生可以体会不同处理方法的优劣势.
5.用数学思维感悟责任担当———建立正确的价值观.学生能在本节课学习中形成理性精神、科学责任、实证意识,增强数形结合的意识和能力,掌握由具体到抽象的研究方法,形成联系与变化的认识观.
三、教学内容
第一阶段:创设情境,引入课题
情境1:向高为H,体积为V的容器中注水,注满为止.图1是水深y与注水量x之间的函数关系的大致图像,问曲线①②分别对应右图的哪个容器呢?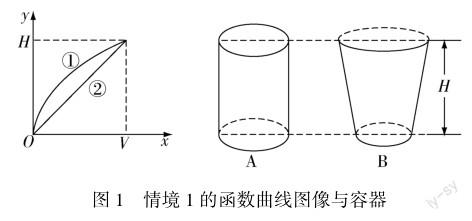
由函数图像可以看出,随着注水量x的增加,曲线①的递增速度在减慢,图像上升趋势变缓,其原因是容器B平行于底面的截面的半径由下底面到上底面逐渐变大,所以曲线①对应的是容器B;曲线②的递增速度不变,所以曲线②对应的是容器A.
情境2:某地某段时间的气温变化图,横坐标是天数t,纵坐标是温度T.
观察图2中曲线的AB段和BC段,会发现BC段气温上升得快.而曲线AB段气温变化为15.1℃,曲线BC段气温变化为15℃,所以曲线AB段气温变化略大.那为什么反而是曲线BC段气温变化更快呢?因为曲线AB段所用时间为31天,曲线BC段所用时间为2天.快慢不仅要看气温变化的大小,还要看时间变化的长短.
在曲线BC段上,气温由18.6℃上升到33.6℃,说明在短短两天时间内,人们感受到天气突然变热了.从点B到点C气温值的“陡增”,在数学上要如何量化呢?由变化图可知只考虑气温差不够,还需要考虑时间差.
第二阶段:归纳探索,形成概念
1.结合实际,归纳总结
物理学中,速度表示物体运动的快慢和方向.在数值上,速度等于物体运动的位移与这段位移下所用的时间的比值.路程是时间的函数,温度也是时间的函数,包括前面高度是注水体积的函数,因此,将函数值的差比上自变量的差的比值称为函数的平均变化率.
2.共同探讨,形成概念
学生共同探讨研究,总结出函数平均变化率的概念.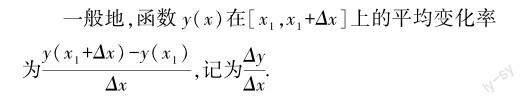
情境3:
在实际生活中,我们不仅关心数量的增加,还关心增加的快慢.比如,粮食年年增加,人口也在增加,如果人口增加的程度超过了粮食产量的增加程度,那么有可能会发生粮食危机.人口、粮食模型比较复杂,教师可带领学生对比一些具体的、熟悉的函数递增的快慢情况.
设计意图:通过几个情境,引导学生观察图像,培养学生核心素养中的直观想象能力,使其能直观判断函数递增的快慢,给出函数递增快慢的猜测,并能叙述平均变化率的概念和计算公式.
第三阶段:掌握概念,学会运用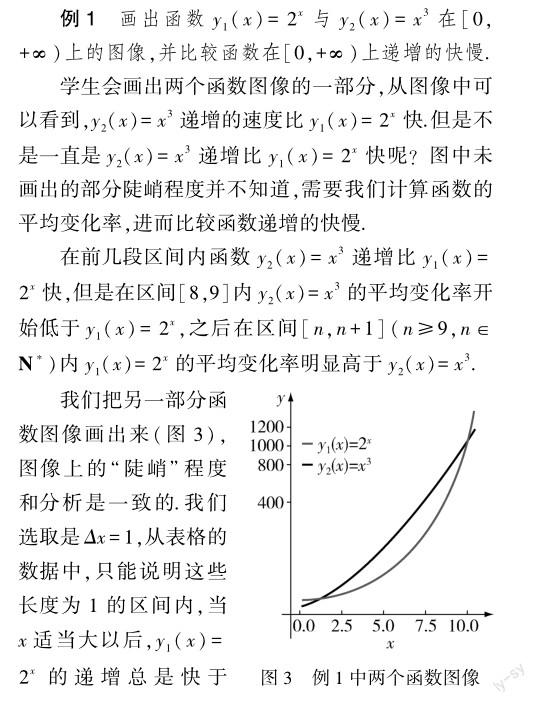

第四阶段:归纳小结,提高认识
函数递增的快慢是单调函数的重要性质.函数递增的快慢是平均变化率的“视觉化”,平均变化率是函数递增的快慢的“数量化”.“观察→归纳→猜想→证明”是科学研究的途径和路线之一,也必然是数学科学研究的途径和路线之一.数学教育家波利亚特别强调,在数学教学中既要有演绎推理,又要有合情推理,也就是说既教证明,又教猜想.本课的两个例题的教学过程,既是对这一教学理念的解读,又是数形结合的体现,从图像观察到理论证明到实际应用.
四、教學反思
本节课采用“观察—归纳—猜想—证明”的研究思路,让学生体会可以利用平均变化率来比较函数递增的快慢,为以后学习导数做好铺垫,也为今后进一步学习微积分奠定基础.
平均变化率可以正,也可以负.本节课没有涉及平均变化率为负值的情况.但学生一旦有了正的变化率的感知和理解之后,只要稍微点拨一下,就很自然地得到负的变化率的感知和理解.在例2中,本意是想让学生用代数证明的方法计算平均变化率,而学生理解成了公式的变形.只有少部分学生使用了数形证明,大多数在取特殊值并填表.自主的探究方法是好的,但是教师没有给出一个明确的研究方向.因此,教师不仅要给学生自主探究的空间,也需要适时地给一些解决问题的方向.
所以,总的来说,课堂上,教师要增加课堂情趣,加强直观到抽象的引导,在数形结合和情境认知中发展学生的抽象思维能力、符号意识,强化课堂的基础训练,提高学生解题的速度和效率.
【参考文献】
[1]严桂光.核心素养背景下的高中数学课例研究与实践———以“直线与平面垂直的判定”为例[J].新课程评论,2018(4):65-74.
[2]林立新.浅谈中数教学中学生推理能力的培养[J].飞(素质教育版),2014(3):98.
[3]傅艺珊.基于核心素养导向的高中数学智慧课堂教学设计———以人教A版《椭圆及其标准方程》为例[J].福建中学数学,2022(01):41-44.

