转化思维在小学数学解题中的应用探析

王国峰

摘 要： 把问题元素从一种形式转化为另一种形式，这种思维就是数学转化思维.在学生解答数学问题时，“转化思维”可以起到非常巧妙的作用，教师灵活的运用转化思维，能够让学生紧紧地抓住数学题目中所蕴含的关键点，让学生拥有更强的逻辑思维能力，更容易理解题中的重点、难点，让学生解题的过程变得更加轻松容易.本文就根据目前的实际状况，研究如何在小学数学解题教学中落实转化思维方式的教学，以期望为更多的教学者带来典型示范.

关键词： 小学数学；解题；转化思维；应用

灵活的运用转化思维，可以将问题由繁化简，由难化易，从复杂到简单的思维过程就是转化思维的灵魂所在，在数学学科教学中使用的也较为广泛，是探索知识和解决问题过程中最有效也是最常用的一种方式.在小学的数学课程教学中，转化思维必须要灵活的运用，让教师鼓励学生自主学习，引领学生将复杂的知识点转化为简单的知识点，共同领会数学的奥义.在如今的新课改环境之下，小学数学课堂使用了众多的教学方式和手段，但是在真正教学时依旧会出现各种缺漏.比如教师无法充分的了解学生的状况，影响在课堂之上题材的选择，导致部分学生无法跟上学习的进度.教师要仔细的钻研教材，同时也要钻研学生，从学生的心理想法出发，制定有关的教学计划，不仅符合教学逻辑，更要以培养学生的核心素养为第一重点教学.

1 转化思维的内涵

在数学思维中，转化思维是极其重要的.小学学生在解答数学难题时使用到转化思维方式，能够有效地将困难的问题转化为简单的问题，最终提高解决问题的效率.一般来说，转化思维是一个由繁到简的过程，想要把复杂的问题变得简单，就要找到题目中所蕴含的深层条件，把模糊的条件转化为具体的条件，将不规则的图形变为规则图形.

2 转化思维在小学数学解题中的重要意义

2.1 培养学习兴趣，提升教学质量

大部分的教师还是会受到传统的教学观念影响，导致在教学时使用到的教学方式依旧是單方面的灌输，削减了学生学习的热情.小学数学在进行解题过程中，使用到转化思维能够帮助学生提升自身解决问题的能力，保障效率的同时也能够提升准确度，还能够让学生获得自我满足感，激发学生的学习热情.学生掌握了正确的解题思路之后，也可以反馈给教师，使教师能够找到更好的途径教导学生提升课堂的教学质量.

2.2 知识化繁为简，培养数学思维

从目前的发展状况而言，在学生日常学习的过程中，有些过于困难的思维能力题会让学生望而却步，这也就代表学生必须要掌握正确的解题思路.教师熟练地运用转化思想，将题中的困难知识点转化为容易理解的知识点，方便学生去解答难题，提升学生的思维能力.利用转化思想，让学生将生活中常见的问题转化为数学问题，从而能够更容易掌握复杂难懂的数学知识，在生活常识的基础之上解决问题.

3  转化思维在小学数学解题中的有效应用策略

3.1 转化思维在计算题中的应用

数学学科的核心素养众多，其中最为重要的就是计算能力，所以如果想要让学生能够迅速地解答数学问题，教师要有意识地引导学生提升转化思维的能力，让学生有正确的解题思路，提升学生学习的热情，帮助学生打下转化思维形成的基础.

比如在教学人教版五年级数学上册“小数乘法”和“小数除法”这一部分的内容时，可以根据有关题目切入，让学生的思维得以转换，打通另一条学习道路，让学生体会到学习的便捷性，还可以让学生有更为迅速准确的解题方案，养成良好的解题习惯，促使学生日后更积极的解答问题.除此之外，在教学时，教师要时刻注意自身对学生的引导作用，让学生仔细观察，找到算式的特点，从而能够更方便学生扭转知识难点，化繁为简，让解题变得更加高效准确.长此以往进行下去能够有效提升学生的逻辑思维能力，改善思维方式.

3.2 转化思维在几何题中的应用

在小学课堂教学中，几何知识教学不仅是教学重点，还是教学难点.因为抽象的几何知识对于学生来说过于晦涩难懂，会导致学生的学习质量下降，在做有关几何知识的题目时，学生往往会更容易受挫，无法灵活运转去解答题目.这就要求教师在进行几何教学时，可以有效地利用多媒体软件，提升学生的观察和理解能力，利用数形结合的方式帮助学生直观地感受到图像的变化，以此让学生对图形的感知能力得以增强，在这种教学方式中，能够有效地让学生了解转化思维的重要，帮助学生提升转化思维能力.分析能力和思维能力的培养在数学学习中是必不可少的，也是能够让学生更好地解决数学知识的重点.利用数形结合的方式展开教学，促使学生的思维能力得到显著的提升.正常来讲，数形结合的方式在小学数学课堂中发挥着巨大的作用：第一，方便学生理解数学知识，帮助学生接纳课堂内容，让学生更为牢固的记住所学的知识，提升逻辑思维能力.利用数形结合的方式讲解，让学生的推理能力得以增强，提高学习的效率.第二，让学生的解题思路变得更加清晰.数形结合的方式可以有效地将数学问题变成一个整体，促使学生系统地理解问题，从而找到更完美的解决方案.数形是息息相关的，两者之间可以实现相互转换，从而更高效地解决数学问题，教师可以使用多种教学方式，把图形问题变得更加生动，让学生掌握图形规律.

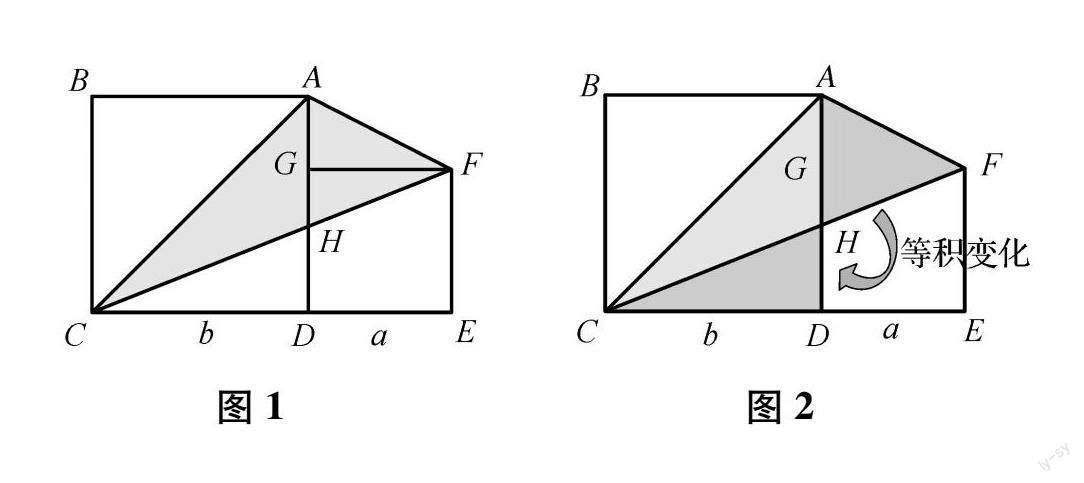
这一部分的教学因为涉及到图形面积，所以过于困难，导致学生在学习的过程中愁眉不展，如果能够应用转化思维，将化解学习难度.正是因为这样，所以在进行课堂教学时，转化思维的使用能够有效地帮助学生解答难题.更准确一点来说，就是在课堂上如果有和图形相关的知识计算题，可以让学生改变以往的解题思路，引导学生使用转换思维的方式，将一个大的图形分解为几个小图形去计算，将所计算出来的图形面积相加在一起，得到最终答案，促使学生更顺利地解决难题.比如人教版五年级上册“多边形的面积”这部分内容在学习时，教师要有意识地引导学生将转化思维发挥出来.比如如下这个题目，图1，求出阴影部分的面积.教师就可以利用数形结合的方式，把这个问题的解题思路梳理出来：

① 由图1可看出，梯形EFAD的面积可以表示为（a+b）×a÷2，三角形EFC的面积可以表示为（a+b）×a÷2，两个图形的面积是一样的.②三角形HAF的面积=梯形EFAD的面积-梯形HDEF的面积，而三角形HDC的面积又等于三角形CFE的面积-梯形HDEF的面积，所以就可以得出三角形HDC的面积和三角形HFA的面积是相等的.通过这样的解题思路，如图2，学生很容易就得出最终阴影部分的面积为 b2 2 .

从这个例题之中可以发现在解答几何题目时，将一个大的不规则图形转化为几个小的规则图形计算，可以提高计算效率，这其中就使用了转化思维，所以在小学数学教学时，教师要熟练地运用转化思维.

3.3 转化思维在小学数学方程题目中的应用

小学数学的另一个重要知识点就是方程问题，学生要想熟练地掌握解答方程问题的方式，必须要找到方程之间的变量关系，了解题目中的未知量，从而建立方程.寻找未知量之间的关系就是一种转化思维的过程，需要学生全面地考虑，才能够构建一个正确的方程.

以小学数学六年级下册中“在底面半径为6  cm ，内部水高为12  cm 的圆柱水缸中，放一个底面半径为5  cm 的圆锥形铅锤完全浸没其中，水没有溢出，此时水面的高度为14.5  cm ，求圆锥形铅垂的高.”这一题为案例：首先让学生理解题目的意思，然后说出自己的想法.学生1：首先要把14.5  cm 圆柱的体积求出，然后再求出高为12  cm 的圆柱的体积，最后把大的体积减去小的体积，从而得到圆锥的体积；有了圆锥的体积之后，就可以根据半径求出圆锥的高.列式是：3.14×6×6×14.5=1 639.08（立方厘米），3.14×6×6×12=1 356.48（立方厘米），1 639.08-1 356.48=282.6（立方厘米），282.6×3÷（3.14×5×5）=10.8（厘米）.学生2：首先求出水面圆柱上升的体积，圆锥形铅锤的体积实际上就是上升的体积，得出圆锥的体积就可以求出高.列式是：3.14×6×6×（14.5-12）=282.6（立 方厘米），282.6×3÷（3.14×5×5）=10.8（厘米）.老师可以着重表扬学生2，能够熟练地运用转化思维将圆锥的体积看成水面上升的圆柱体积去解答问题.不过这两种方法都不是最简单的，最好的解题方式就是先把铅锤的体积和上升水柱的体积互换，使用“圆锥的体积等于水面上升的圆柱的体积”这个等量关系去建立方程：

解：设这个圆锥形铅锤的高是x厘米，则

  

   1 3 ×3.14×5×5×x= 3.14×6×6×（14.5-12），

 1 3 ×3.14×5×5×x = 3.14×6×6×（14.5-12），

         25 3 x = 90，

      所以，x =  54 5 ＝10.8.    

根据这种能量转换方程，可以更加迅速地解答知识.让学生熟练地运用转化思维，理清题目中的各种等量关系，可以迅速地建立方程，并且快速的求出方程中的未知量.其中，方程问题的假设时，要让学生熟练地运用转化思维，能够更快的构建方程式，求出未知值.

    4 结语       

综上所述，小学数学解题过程中应当教会学生熟练地运用转化思维，能够提升解题效率.转化思维在数学解题过程中是极其重要的，所以教学时，所有能够使用到转化思维的内容，教师都要敏锐的察觉，并且灵活的运用其中，帮助学生改变做题方式，提升思维转化能力.其中在小学数学计算、几何和方程式等内容中，是最能够体现出转化思维重要的，也是最容易培养学生的转化思维能力，要在此部分内容的学习过程中培养学生良好的解题习惯.而且学生在解答时，教师可以适当地给予指点，方便学生能够从解题的过程中积累经验、获取知识，从而更熟练地运用转化思维去解答难题.

  参考文献：   

  

［1］ 钟晓武.关于小学数学解题中转化思维的有效应用分析［J］.新课程（上），2019（6）：70.

［2］ 于新星，王琴.转化思维在小学数学解题中的有效应用探讨［J］.中国多媒体与网络教学学报（下旬刊），2022（11）：91 94.

［3］ 吴云泽.小学数学解题中转化思维的有效应用分析［J］.数学学习与研究，2022（18）：93 95.

［4］ 徐建干.转化思维在小学数学解题中的有效应用［J］.数学教学通讯，2022（13）：69 70.

［5］ 陈丽.小学数学解题中转化思维的有效应用［J］.家长，2022（9）：141 143.

［6］ 林瑛.转化思维在小学数学解题中有效应用的对策探讨［J］.考试周刊，2021（25）：79 80.