例说“拼图法”在初中数学解题中的应用

王佳

摘 要： “拼图法”主要是指依据数学问题的具体解决需要，有意识地把几个图形都拼合到一起，并参照拼图之前与拼图之后的图形面积、周长与角度等，对相关数学问题进行解决.鉴于此，本文主要对“拼图法”在数学解题当中的巧妙运用进行探讨，找出解题的新思路，以实现数学问题的高效解决.

关键词： 初中数学；拼图法；解题；策略

新课标下，新的数学教材当中的几何内容明显要比先前的内容丰富.图形变化也属于“图形与几何”当中的主要内容，其充分体现出了几何的价值取向，即空间观念、几何直观等素养与能力培养.“拼图法”常见的方法有翻折、平移与旋转，拼图的过程常常会涉及位置与方向的改变，这都需要开展观察、比较、想象以及推理等一系列的思维活动，其是对学生空间观念进行培养的有效载体.同时，经过翻折、平移与旋转等方式进行拼图，让图形真正的动起来，则能在该过程中发现图形始终不会改变的性质，由此可知，拼图法是解决相关几何问题的有效方法，能够使学生实现高效解题.

1 巧用“拼图法”作辅助线

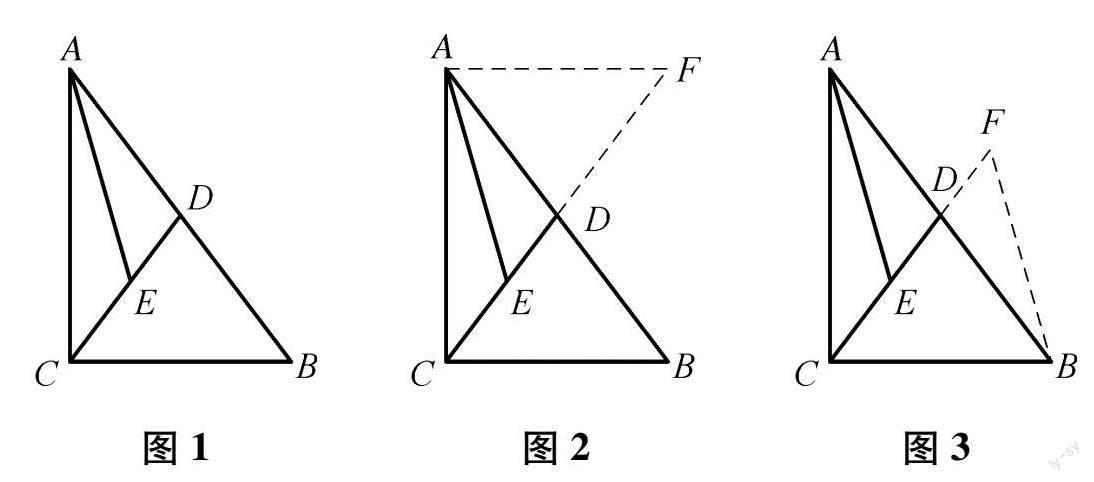
例1     如图1所示，在 Rt △ABC中，AC＞BC，∠ACB=90 ° ，CD为△ABC的中线，E点位于CD上，且有∠AED=∠B，证明：AE=BC.

解析：    学生依据自身经验，就能联想到倍长中线法，如图2、3，其主要的目的就是经过图形旋转，将需要证明的线段AE与BC置于同个三角形，形成等腰三角形，以实现问题的有效解决.上述问题，也能当做是将复制的△CBD或者是△ADE拼成图2、图3.以△ADE为例，将△ADE拼到其他的位置，则能找出相应的辅助线.

解答：    方法一：以AD=CD=BD当做拼图条件.

现已知图形当中的线段AD、CD、BD是相等的，将复制的△ADE当中的线段AD和已知图形当中的CD、BD分别进行重叠，试着拼出图4、图5、图6.

如图4所示，拼图之后，会发现构成等腰三角形CBF，那么就可以作辅助线：在线段AB上取F点，确保CF=CB，以此便可证明△ADE≌△CDF，即可证AE=BC.

如图5所示，拼图之后，连接BF，则有BF∥AE，同时形成等腰三角形CBF，此时，作辅助线：过B点作出BF∥AE，且∠DCF=∠DAE，CF分别与BD、BF相交于O、F两点，连接DF，可证明出∠CDB=∠CFB，又有∠CDB=∠DAE+∠AED，∠CBF=∠CBD+∠DBF，那么∠CDB=∠CBF，所以∠CBF=∠CFB，因此，CB=CF，由此可证：∠AED=∠CFD，所以，△ADE≌△CDF，所以AE=CF，也就是AE=BC.

如图6所示，拼图之后，可发现形成了等腰三角形OCF与等腰三角形OBD，可作辅助线：过C点作出CF∥AB，并使CF=DE，连接DF，且与线段BC相交于O点，以此可证明△ADE≌△DCF，且∠CFD=∠AED，由此可证OB=OD，OC=OF，那么可证明AE=BC.

方法二：以AE=BC当做拼图条件.

试题中要求证明AE=BC，将复制出的△ADE当中的AE和已有图形的BC重叠，可拼出图7、图8.

如图7所示，拼图之后，会发现构成等腰梯形CFBD，可作辅助线：经过C点作出CN∥AB，在射线CN上取F点，使BF=CD，此时，四边形CFBD为等腰梯形，即可证明∠ADE=∠CFB，从而证明△ADE≌△BFC，即AE=BC.

如图8所示，拼图之后可形成等腰三角形BDF，作辅助线：在CD上取F点，使BF=BD，即可证明∠ADE=∠BFC，也就是△ADE≌△BFC，即AE=BC.

2 巧用“拼图法”解证明题

例2     如图9所示，在 Rt △ABC与 Rt △A′B′C′中，AB=A′B′，AC=A′C′，∠C=∠C′＝90 ° ，证明： Rt △ABC≌ Rt △A′B′C′.

证明： 因为AC=A′C′，所以把 Rt △ABC与 Rt △A′B′C′拼合到一起，形成图10，确保A与A′是重合的，且C与C′是重合的，所以∠BCB′=∠ACB+∠A′C′B′=90 ° +90 ° =180 ° .因此，B、C、B′三点共线，又由于AB=A′B′，因此∠B=∠B′.又因为∠BCA=∠B′C′A′，即得 Rt △ABC≌ Rt △A′B′C′.

例3     如图11所示，钝角三角形ABC与钝角三角形A′B′C′当中，AB=A′B′，AC=A′C′，∠B=∠B′（∠B为钝角），证明：△ABC≌△A′B′C′.

证明： 因为AC=A′C′，所以可将△ABC与△A′B′C′ 拼合到一起，让A与A′重合，C与C′重合，连接BB′，详见图12，由于AB=A′B′，即∠1=∠2，又有∠ABC=∠A′B′C′，因此∠ABC-∠1=∠A′B′C′-∠2，也就是∠3=∠4，因此BC=B′C′.在△ABC與△A′B′C′当中，AB=A′B′，AC=A′C′，BC=B′C′，由此可证△ABC≌△A′B′C′.

例4     如图13，在 Rt △ABC中，∠B=90 ° ，BC= 1 2 AC，证明：∠A=30 ° .

证明：     将另一个和 Rt △ABC全等的 Rt △ABD与 Rt △ABC依照图14的方法拼到一起，那么∠CBD=∠ABC+∠ABD=90 ° +90 ° =180 ° ，由此可知，B、C、D三点是共线的，即CD =BC+BD=2BC=AC=AD，△ACD为等边三角形， 即∠CAD=60 ° ，所以∠CAB= 1 2 ∠CAD= 1 2 ×60 ° =30 ° ，也就是∠A=30 ° .

3 巧用“拼图法”解实际问题

3.1 解圆的问题

例5     如图15所示，在△ABC中，∠A=120 ° ，AB=AC=5，则△ABC外接圆的半径R是多少？

解答：    依据垂径定理可知：作△ABC的外接圆O，且OA为∠BAC平分线，由此可知，∠OAC= 1 2 ∠BAC=60 ° ，连接OC，即OC=OA，此时，三角形OAC为等边三角形，即OC、OA、AC是相等的，都是5，所以外接圆的半径R=5.

例6     如图16，圆O的半径为13，其弦AB的长度是24，且AB的中点为M，而P点为圆上的动点，则PM的最大值为多少？

解析：    依据题意可知：OM+OP≥PM，按照点圆模型的具体原理，在O、P、M三点共线的时候，PM可取最大值，则有PM⊥AB，且过点O，即点P处于P′的时候，PM值最大.

解答：    如图17所示，连接OA，依据垂径定理，得AM= 1 2 AB=12.在 Rt △AOM中，OA=13，根据勾股定理，得OM=5，所以P′M=OM+OP′=18，即PM的最大值为18.

3.2 解三角形的问题

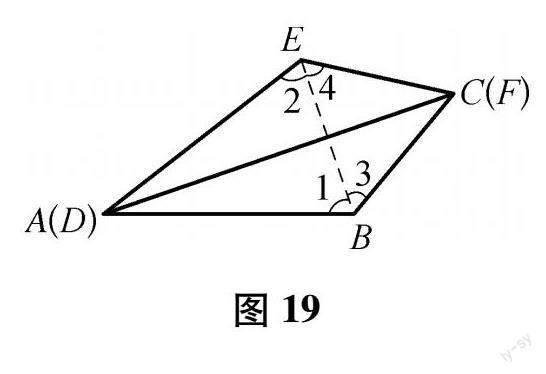
例7     如图18，在△ABC与△DEF中，AB=DE，AC=DF，且∠B=∠E，∠B、∠E均为钝角，证明：△ABC≌△DEF.

证明：    依据题意，如图19所示，把AC和DF拼到一起，使A点和D点两点重合、C点与F点两点重合，让∠B和∠E分别位于AC或者是DF两侧，连接BE，依据AB=DE，可得∠1=∠2，又有∠ABC=∠DEF，因此∠ABC-∠1=∠DEF-∠2，由此可得∠3=∠4，所以BC=EF，按照“边边边”，可证得△ABC≌△DEF.

3.3 解一元二次方程式问题

例8     已知长方形的宽与长之和是7，其面积是10，求长方形长和宽之差的平方.

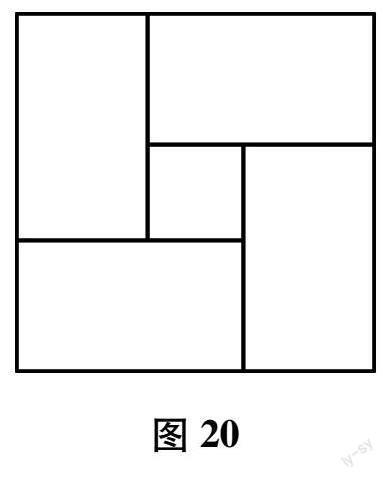
解析：    本题如果依据常规方法进行求解，则设长是a，宽是b，按照题意，可得到：a+b=7，ab=10，那么长和宽之间差的平方是（a-b）2，想要求出（a-b）2的具体值，可以把（a-b）2转化成包含a+b与ab的式子，也就是（a-b）2=a2+b2-2ab=（a2+b2+2ab）-4ab=（a+b）2-4ab=49-4×10=9.除去这种直接解法，还可以巧妙地运用拼图法加以求解，如图20所示，将其拼到一起，则能拼成大的正方形，该正方形边长恰好为长方形长和宽之和，中间的小正方形，则为其长和宽之间的差.

解答：    经过对图20进行观察可知，大正方形面积与4个长方形面积相减，就是小正方形的面积，也就是S 小正方形=S 大正方形-4S 长方形=72-4×10=49-40=9，因此长方形长和宽之间差的平方值是9.

4 结束语

综上所述，将“拼图法”运用于初中数学的解题中，既能呈现出化难为易、化繁为简的效果，又能充分呈现出数学问题的魅力.因此，在初中数学解题教学中，教师需注重“拼图法”的运用技巧与方法，从而使学生的解题效率得到有效提高.

参考文献：

［1］ 刘淑锦.例说“拼图法”在初中数学解题中的应用［J］.数理天地（初中版），2022（10）：22 23.

［2］ 周喆.拼图法在初中数学解题中的應用［J］.数学大世界（下旬），2021（7）：75 76.

［3］ 朱玉平.例说“拼图法”在初中数学解题中的应用［J］.中学数学，2019（8）：79 80.

［4］ 吴玲芳.数学实验探究课：“拼图”［J］.中小学数学（初中版）， 2018（4）：17 22.

［5］ 张伟俊.数学综合与实践活动中的教学策略：以“拼图·公式”的教学为例［J］.中小学数学（初中版），2022（7）：116 119.

［6］ 汪东松.对“拼图”教学的点滴思考［J］.中学数学， 2022（14）：34 35.