四元数双向联想记忆神经网络的固定时间控制

石雨晨，魏若宇

（1.南京信息工程大学 数学与统计学院，江苏 南京 210044；2.南京信息工程大学 江苏省应用数学中心，江苏 南京 210044）

人工神经网络是一种模拟人脑神经系统结构和功能的非线性处理系统，是生物神经网络的数学抽象[1]。双向联想记忆神经网络（bidirectional associative memory neural networks，BAMNNs）是一种著名的网络模型，由Kosko 在1987 年首次提出[2]。该网络通过上下两层间信息的迭代，具有信息关联能力和信息记忆能力。它可以将存储在内存中的完整、清晰的模式与不完整或模糊的模式相关联[3]。因此，该网络在模式识别、信号与图像处理、人工智能等领域都有较好的应用。这些应用在很大程度上依赖于网络的动力学行为。近年来，人们对BAMNNs的动力学行为进行了广泛的研究，如指数稳定性、同步、拉格朗日稳定性、耗散性等[4-6]。然而，目前对BAMNNs 动力学行为的研究主要集中在实数域和复数域，对四元数域的研究还很少。

1843 年，英国数学家Hamilton 首次提出了一种特殊类型的Clifford 代数，称为四元数[7]。与实数和复数不同，四元数的一个重要特征是不适用乘法的交换律。由于这个原因，四元数的发展受到了很长时间的阻碍。近几十年来，四元数系统因其在量子力学、姿态控制、彩色人脸识别、计算机图形学[8-12]等方面的广泛应用前景而成为研究热点。

近年来，一些研究者在传统神经网络中引入了四元数，从而建立了四元数神经网络（quaternionvalued neural networks，QVNNs）。QVNNs 可以看作是实值神经网络（real-valued neural networks，RVNNs）和复值神经网络（complex-valued neural networks，CVNNs）的推广，其中神经元状态、连接权值和激活函数都是四元数。与传统的神经网络不同，QVNNs在处理多维信息方面具有显著的优势。例如，在图像处理中[8]，与RVNNs 或CVNNs 相比，QVNNs 可以显著减小系统的规模，从而带来计算效率的提高。此外，QVNNs 相比RVNNs 和CVNNs 具有更好的性能，可以处理一些优化和估计问题[12]。递归神经网络构成一个动力系统，其动力学行为可广泛应用于联想记忆、优化计算、鲁棒控制、模式识别等领域。因此，动力学行为的研究是神经网络应用的基础。最近，在QVNNs 的动力学行为分析方面已取得显著的研究进展，如耗散分析[13]、稳定性[14-16]、状态估计[17]。然而，目前关于QVNNs 有限时间同步的研究还较为稀少。

同步现象是一种典型的集群动力学行为，由于其在联想记忆、组合优化和模式识别等方面具有广泛的潜在应用，已受到学术界的极大关注。同步是指两个或多个系统状态趋同的动力学行为，如神经网络中经常出现的混沌行为。近几十年来，出现了大量关于渐近同步和指数同步[18-19]的研究工作。然而，由于工程设备的寿命有限，渐近同步在许多实际应用中并不适用。因此，为了满足实际需要，研究者提出了有限时间稳定性[20]的概念。从本质上讲，有限时间同步保证了系统误差在有限时间内收敛到0。然而，有限时间控制的局限性在于：其收敛时间依赖于误差系统的初始信息[21-22]。事实上，许多实际系统的初始信息有时是无法提前获得的。针对该缺陷，有学者引入了固定时间控制的思想[23]，该方法的优势在于：在系统初始信息未知的情况下，可以估计出收敛时间的上界。由于这种巨大的优越性，固定时间控制已经引起了学术界的高度重视并广泛应用于工程实际中[24-26]。

此外，在已有的神经网络动力学文献中，激活函数通常被假设为连续的甚至是Lipschitz 连续的。事实上，这种假设过于严格，对于一些实际工程问题，该假设可能存在较大的局限性。需要指出的是，具有不连续激活函数的神经网络是一种更为符合实际的模型，特别是在处理高维非线性物理问题[27-28]时具有显著的优越性。到目前为止，关于非连续四元数神经网络的固定时间同步问题的研究还较为稀少，但富有实际意义。因此，本项研究工作是具有研究意义和挑战性的。

基于以上介绍，本文将探索具有不连续激活函数的四元数双向联想记忆神经网络（quaternion-valued bidirectional associative memory neural networks，QVBAMNNs）的固定时间同步控制问题。本文的主要创新点可以概括为：

1）在BAMNNs 中引入四元数，既满足了对大容量存储空间的需求，又降低了联想记忆过程中的保守性。

2）本文假设四元数激活函数在每个虚部是不连续的，这在工程应用中很实用，但在以往对四元数神经网络的研究中并不常见。

3）与传统的渐近同步不同，本文研究了QVBAMNNs 的固定时间同步问题，其中收敛时间可以在系统初始条件未知的情况下被确定。

注1在本文中，R、C 和Q 分别表示实值、复值和四元数值。对于任意向量χ=（χ1，χ2，…，χn）T∈Rn，规定。对任意向量x，y∈Rn，i=1，…，n，x≤y 意味着xi≤yi。1-向量范数定义为对于任意矩阵A∈Rn×n，1-矩阵范数定义为

1 模型及预备知识

四元数是复数的扩展，由1 个实部和3 个虚部组成。四元数y∈Q 可以写成

其中yR，yI，yJ，yK∈R，虚部i，j，k 满足Hamilton法则：

注2由Hamilton 规则可以看出交换律不适用于四元数的乘法，即：对任意y，z∈Q，不能保证yz=zy。这一缺陷增加了四元数神经网络动力学行为研究的难度，现有的分析实值和复值神经网络的技术手段不能直接应用于四元数神经网络。因此，有必要开发新的分析方法来研究四元数神经网络动力学行为。

对于任意两个四元数，y=yR+yIi+yJj+yKk和z=zR+zIi+zJj+zKk，它们之间的加法定义为y+z=yR+zR+（yI+zI）i+（yJ+zJ）j+（yK+zK）k。根据Hamilton 规则，任意两个四元数之间的乘法定义为

基于此，建立四元数双向联想记忆神经网络（QVBAMNNs）模型

其中：xp（t），yq（t）∈Q 分别表示在FX域上第p 个神经元和在FY域上第q 个神经元的状态值；r1p，r2q∈R 为自反馈连接权重，且满足r1p，r2q＞0；apq，bpq，cqp，dqp∈Q 为连接权重；fq（yq（·）），gp（xp（·））：Q→Q 分别表示在FX域上第p 个神经元和在FY域上第q个神经元的状态值激活函数；时滞τ（t）满足τ˙（t）≤ρ ＜1，0≤τ（t）＜τ，ρ 和τ 为正常数。

在本文中，我们考虑m=n 的特殊情况：

系统（2）的初始值表示为xp（s）=φp（s），yq（s）=φq（s），-τ≤s≤0。我们的目的是探索主从系统的固定时间同步，系统（2）作为主系统，选择受控从系统如下所示：

注3根据四元数和BAMNNs 的特点，将其应用于联想记忆领域关键在于解决动力学分析的问题。四元数BAMNNs 的固定时间同步控制研究为非线性系统的动力学分析提供了新的研究思路。

假设1假设四元数值的激活函数fq（yq（t）），gp（xp（t））可以分解成以下形式：

根据Hamilton 规则，四元数系统（4）可以分解为如下4 个实值系统：

注4与普通神经网络相比，具有联想记忆函数的神经网络的实现需要满足更多的条件：第一，当且仅当网络中存在渐近稳定平衡点时，可作为存储的记忆模型；第二，即使在记忆模式吸引区噪声污染很小的情况下，系统状态轨迹仍能收敛到存储模式；第三，网络需要有尽可能多的存储容量，这样新模式在存储时才不会影响网络中给定的平衡点。此外，网络还应具有执行力强、适应性强、鲁棒性强的特点。

注5由于四元数乘法的不可交换性，直接处理四元数系统（4）具有很大的难度。因此，本文采用四元数分解方法。联想记忆的实现依赖于神经元簇的活动，神经元的状态反映了联想记忆的功能。因此，误差系统的稳定性在联想记忆机制中是必不可少的基本条件。

令

则系统（6）—（9）可改写为

其中

对响应系统（5）进行类似转换，可以将响应系统（5）转化为

其中

我们的目的是设计适当的控制器U（t），V（t），以获得主从系统（10）和（11）的固定时间同步。令，得到误差系统为

其中：

为后续讨论方便，记

由于原系统（4）—（5）与转换后的系统（10）—（11）等价，以下对转换系统（10）—（11）假设可以从假设2 直接得出。

假设3对于转换系统（10）—（11），激活函数Fi（·），Gj（·），i=1，…，4n，j=1，…，4n 除可数个不连续点以外在R 上都是连续的，并且存在非负常数使得

定义1对于右边不连续的方程组，如下所示：

其中x（t）∈Rn，f（t，x（t））：[0，R）× Rn→Rn，是局部本性有界和勒贝格可测的。Filippov 意义下的解是一个绝对连续函数x（t），t∈[0，t]，它满足

其中集值图K[f（t，x（t））]定义为

定义2设E（t）=（Ex（t），Ey（t））T，对于系统（12）的初始值E（t0），如果存在某个常数T（E（t0））使得

则四元数主从系统（2）和（3）可以实现有限时间同步，T（E（t0））定义为收敛时间。

引理1[20]假设函数V（·）：Rn→R+∪{0}是连续的完全有界函数，满足以下条件：

1）V（x）=0 ⇔x=0，

2）对于系统（12）的任意解E（t），它满足

则原误差系统（12）可以达到有限时间稳定。估计收敛时间为

引理2[23]假设函数V（·）：Rn→R+∪{0}是连续的完全有界函数，满足以下条件：

1）V（x）=0 当且仅当x=0，

2）对于系统（12）的任意解E（t），有

此时，原误差系统（12）可达到固定时间稳定，其稳定时间为

引理3[23]假设引理2 中的条件满足，p=1-。此时，系统（12）的原点可以达到固定时间稳定且

引理4对于常数x1，…，xn≥0，0 ＜p ＜1，q ＞1，以下条件成立：

2 主要结果

在本节中，我们将给出主从四元数值BAMNNs（10）—（11）的固定时间同步准则。

为了实现系统的固定时间同步，设计不连续状态反馈控制器

其中：U（t）=（U1（t），…，U4n（t））T∈R4n，V（t）=（V1（t），…，V4n（t））T∈R4n；K1，K2，Θ1，Θ2为待定的正定对角控制增益矩阵；K3，K4，K5，K6，Θ3，Θ4，Θ5，Θ6为可调正定对角常数矩阵。

根据以上讨论，可得以下定理。

定理1在假设1 和2 的条件下，对于i=1，…，4n，j=1，…，4n，如果控制增益k1i，k2i，θ1j，θ2j满足

则在控制器（17）下可实现系统（10）—（11）的固定时间同步，并获得收敛时间的上界为

证明：考虑Lyapunov 函数

其中

计算V（t）沿轨线（12）的导数，可以得到

基于假设3，不连续激活函数满足以下条件：

将式（22）代入式（21），得到

根据定理1 中的条件，可以推导出

根据引理4，有如下结论：

应用类似分析，可以得到

在引理2 的基础上，在控制器（17）作用下，误差系统（12）可以实现固定时间稳定。等价地，系统（2）和（3）实现固定时间同步，收敛时间为

注6要注意的是，状态反馈控制器（17）的每个部分对实现系统的固定时间同步都具有特定的作用。对由不连续点引起的主从系统参数不匹配问题，采用控制项K1sgn（Ex（t）），Θ1sgn（Ey（t））来补偿。控制器的其余部分用于控制收敛时间，实现固定时间同步。在初始条件未知的情况下，可以通过选择不同的系数矩阵来确定收敛时间。

注7基于递归神经网络的联想记忆可以看作是信息的存储。在实际应用中，需要存储的信息量是巨大的。如果增加神经元的数量，就会增加计算设计参数的数量和难度。因此，为了更好地模拟人脑的联想记忆，我们需要设计基于更高容量的递归神经网络的联想记忆。四元数的出现使这种愿望成为可能。四元数神经网络具有比实值和复值神经网络更强的信号处理能力和鲁棒性。因此，四元数值BAMNNs 的研究可以为联想记忆的研究提供一定的理论支持。

注8联想记忆是通过人工神经网络实现的。首先，将记忆模式设计为神经网络的稳定平衡点，即吸引子，则在给定提示信息的输入下，神经网络通过动态进化收敛到一个稳定的平衡点，即记忆所存储的记忆模式。可以看出，吸引子的个数就是神经网络能够存储记忆模式的个数，也就是神经网络的记忆容量。在BAMNNs 中引入四元数，既满足了对大容量存储空间的需求，又降低了联想记忆过程中的保守性。

推论1假设定理1 中的条件仍然成立。如果控制器（17）中的α，β 选择为，则可以通过控制器（17）实现系统（10）—（11）的固定时间同步。收敛时间可估计为

其中λ，κ 由定理1 给出。

证明：根据引理3 可以直接得到结果。

下面我们考虑有限时间同步问题。选择如下有限时间控制器：

其中，K1，K2，Θ1，Θ2为待确定的控制增益矩阵，K3，K4，Θ3，Θ4为可调正定对角常矩阵，用于控制收敛速度，0 ＜α ＜1，则有如下推论。

推论2在假设1 和2 下，如果控制增益k1i，k2i，θ1j，θ2j，i=1，…，4n，j=1，…，4n 满足定理1 中的条件，则通过控制器（29）可实现系统（10）和（11）之间的有限时间同步。估计收敛时间为

证明：考虑与定理1 相同的Lyapunov 泛函

则按照定理1 中相同的分析，可以推导出

注9在以往的神经网络动力学文献中，激活函数通常被假设为连续的甚至是Lipschitz 连续的。本文假设四元数激活函数的每个虚部在某些间断点处是不连续的。显然，连续状态可以看作不连续状态的一种特殊情况。与以往关于QVNNs 的文献[21-25]相比，具有不连续激活函数的神经网络可以更好地揭示高维非线性物理问题的特征，因此本文的结果可以应用到更广泛的工程实际中。

注10在联想记忆过程中，计算速度是非常重要的。与许多渐近同步的结果不同，固定时间同步可以有效提高收敛速度，并给出收敛时间的估计值。同时，它比实值神经网络和复值神经网络具有更好的鲁棒性。

3 仿真算例

为了验证定理的正确性，本部分给出了定理1和推论2 的两个仿真算例。

例1将以下QVBAMNNs 作为主系统：

其中，r1p=r2q=0.5 且xp（t），yq（t），apq，bpq，cqp，dqp∈Q，时滞为τ（t）=0.5sin（t）+0.5，从而满足

从系统为

选取如下不连续激活函数：

因此，定理1 中的条件满足。首先，我们考虑主从系统（32）和（33）之间的固定时间同步。该控制器由式（17）给出。

可调参数选择为k3i=1，k4i=1，k5i=2，k6i=2，θ3j=1，θ4j=1，θ5j=2，θ6j=2，α=0.5，β=1.5。计算得到收敛时间为

在区间[-0.7，0.7]中选择10 个初始条件，误差ex（t），ey（t）实部如图1 所示，表明主从系统（32）和（33）可以实现固定时间同步。由此，验证了定理1 的有效性。

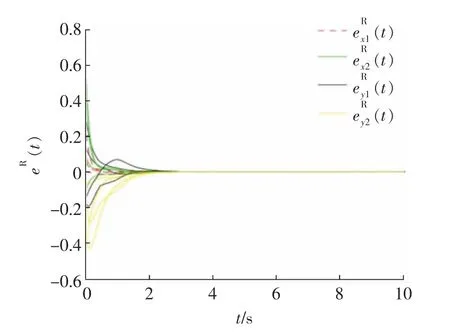
图1 固定时间控制器（17）下主从系统（32）和（33）的误差轨迹Fig.1 The error trajectories of master-slave system（32）and（33）under fixed-time controller（17）

例2考虑与例1 中相同的主从QVBAMNNs模型，选择有限时间控制器（29）。

其中控制增益矩阵K1，K2，K3，K4，Θ1，Θ2，Θ3，Θ4与例1 相同。在区间[-0.7，0.7]内选择10 个初始条件，误差ex（t），ey（t）虚部如图2 所示，表明主从系统（32）和（33）可以实现有限时间同步。从而，验证了推论2 的有效性。

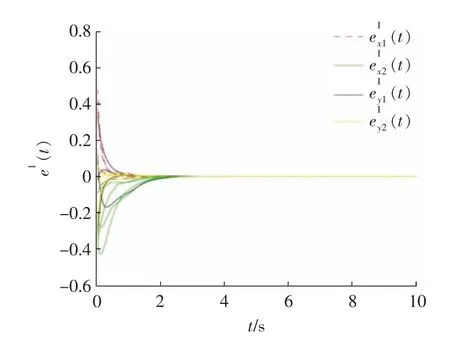
图2 有限时间控制器（29）下主从系统（32）和（33）的误差轨迹Fig.2 The error trajectories of master-slave system（32）and（33）under finite-time controller（29）

注11从仿真结果可看出，实际收敛时间远远小于理论收敛时间。这意味着我们的理论结果还是较为保守的。在今后的工作中，我们将尝试改进固定时间控制策略，以获得更精确的收敛时间估计。

4 结论

本文在传统BAM 神经网络中引入四元数，建立了四元数值BAMNNs 模型。假设激活函数在每个虚部是不连续的，通过四元数分解和微分包含理论，将原始的QVBAMNNs 转化为4 个实值网络。为了实现QVBAMNNs 的固定时间同步，设计了不连续状态反馈控制器，利用Lyapunov 泛函方法，得到了保证主从系统实现固定时间同步的新准则。最后，通过算例验证了本文定理的正确性。