一种基于深度学习的心电图分类方法

高轩瑞，曹进德，张金壬

（1.东南大学 软件学院，江苏 南京 211189；2.东南大学 数学学院，江苏 南京 211189）

根据世界卫生组织（WHO）的调查数据[1]，心血管疾病是当今导致死亡的主要原因。全世界每年超过1 770 万人死于心血管疾病，约占所有死亡病例的31%。在中国，心血管疾病的发病率与致死率高居榜首，仅在2019 年，农村、城市居民的心血管病分别占死因的46.74%和44.26%，这意味着每5例死亡病例中就有2 例死于心血管病。

心律失常是一种具有代表性的心血管疾病的类型，指正常心脏的任何不规则变化节奏。有几种类型的心律失常，包括心房颤动、过早收缩、心室颤动和心动过速[2]等。虽然偶发的短暂的心律失常可能不会对生活产生严重影响，但是持续的心率失常会导致致命的风险[3-4]。因此，定期监测心律以管理和预防心血管疾病是很有意义的，心电图（electro cardio gram，ECG）作为一种显示心律和状态的非侵入性医疗工具，对研究心率变化和诊断心血管疾病有着重要作用。

深度学习方法在图像分类领域有着非常可靠的应用，它能够发现从人类角度无法发现的某些数据的特征。传统的机器学习方法需要细致的分析和精湛的专业领域知识从图像或信号中获取特征进行分析和输入，而深度学习可以自动发现并从原始数据中提取特征。心电图信号作为一种时间序列信号，可以采用深度学习方法进行处理，对信号的类型进行分类[5]，从而减少医生在实际诊断过程中的工作量，提高诊断效率。心电信号强度较低，属于时序微弱信号，信号本身有着非线性随机性等信号特征。心电信号在采集的过程中，也极易受到采集设备及周遭环境的影响，例如周边环境的电磁干扰。此外，身体活动也会对实验结果产生影响，包括躯干的活动、人体正常生理活动如呼吸等，这些因素都会导致采集到的信号会伴随各种噪声，这些噪声包括工频干扰、肌电干扰和基线漂移[6]，见表1。因此，在使用深度学习方法进行辅助诊断的过程中，如果能有效地对初始信号进行去噪，将对实验结果有所改进[7]。

表1 心电信号各频带[1]Tab.1 ECG signals by band[1]

本文使用的数据集是MIT-BIH 心律失常库（MIT-BIH arrhythmia database），该数据集包含48条双通道动态心电信号记录，每一条原始数据都超过30 min，该数据包括25 名年龄在32 至89 岁之间的男性和22 名年龄在23 至89 岁之间的女性，其中有两条数据来自同一个人。在心电信号的滤波方面，主要使用了小波变换方法[8-11]、经验模态分解（empirical mode decomposition，EMD）滤波方法[12-15]及传统的中值滤波方法[16-17]对原始信号进行处理，并使用了卷积神经网络（convolutional neural network，CNN）模型、卷积神经与长短时记忆网络（convolutional neural network_long short-term memory，CNN_LSTM）模型[18-22]对滤波前后的结果进行比较。最后，对模型进行改进，使用加入注意力机制的挤压激励式长短时记忆网络（squeeze-and-excitation network_long shortterm memory，SE-Net_LSTM）模型[23-25]，发现经过滤波后的信号在深度学习分类后能够有效提升分类效果。

1 准备工作

本部分主要进行了数据预处理工作，读取数据集中101 号病人的心电图数据（前1 500 个数据点），如图1 所示，并使用不同的去噪方法进行滤波。

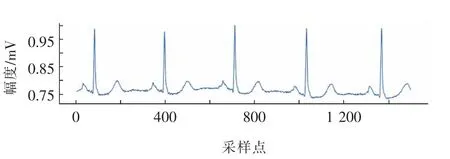
图1 101 号病人的原始心电图数据Fig.1 Raw ECG data from patient 101

1.1 中值滤波方法

中值滤波技术是一种本构的非线性信号处理技术，理论上基于排序统计理论，在心电信号处理的实际应用中，中值滤波器的基本思路是首先去除原心电信号中较大的数值，以获得只存在基线的趋势项信息；接着，将滤除后的信号与原信号重叠，除去原有心电信号中基线漂移的干扰部分，具体如下：

其中，Med[y（1），y（2），…，y（n+R）]是求y（1），y（2），…，y（n+R）的中值。

使用中值滤波方法对心电数据进行滤波后效果如图2 所示。

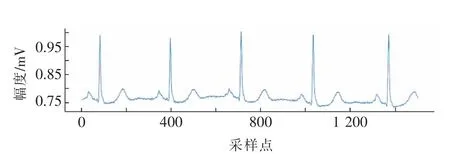
图2 采用中值滤波后的101 号病人心电图数据Fig.2 Median filtered ECG data from patient 101

1.2 小波变换滤波方法

小波变换（wavelet transform，WT）的含义是把某一被称为基本小波的函数做位移τ 之后，在不同尺度α 下与待分析信号X（t）做内积

其中：α 为尺度因子，α ＞0；τ 表示位移，其值可正、可负。

使用离散小波变换分解的过程如图3 所示，对信号进行一步步的分解，其中对低频部分进行多次分解，得到多个不同频率分量。

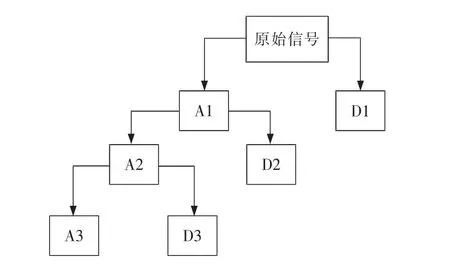
图3 小波分解示意图Fig.3 Schematic diagram of wavelet decomposition

应用小波变换对心电信号进行处理，滤除噪声，具体过程如图4 所示。

图4 小波变换滤波过程Fig.4 Wavelet transform filtering process

1）首先是小波基函数的选择，使用小波基函数对心电信号进行分解，并得到在各个尺度上的小波系数；

2）原信号经过分解后，再对有用信号和噪声信号进行选择，根据心电信号中的有用信号和噪声信号频率分布，对小波系数进行阈值处理；

3）对得到的低频系数和高频系数单独处理，处理完成后重构信号。

1.2.1 小波基函数的选择

多贝西（Daubechies）小波，简写成dbN，N 是小波的阶数。多贝西小波正则性好，使得心电信号在重构过程中比较光滑。

使用dbN 各种小波基函数对数据集101 号病人心电图数据进行滤波，见图5。

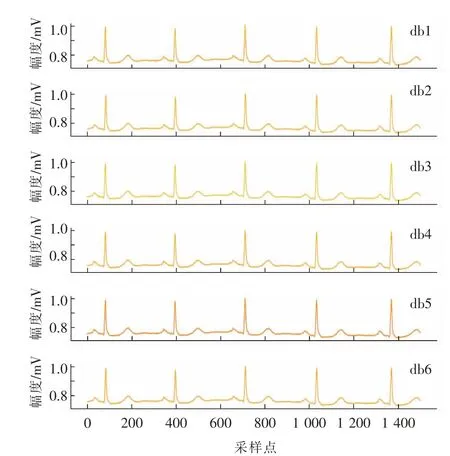
图5 采用dbN 小波进行滤波后的101 号病人心电图数据（N=1，2，…，6）Fig.5 ECG data after filtering using dbN wavelets from patient 101（N=1，2，…，6）

可以发现，当阶数N 较小时，消失矩阶数较小，频带划分效果较差，对信号高频部分的滤波效果不好；当N ＜5 时，P-R 波段和T 波段仍有明显抖动，db6 小波更接近于心电信号，对心电信号去噪有更好的效果。

1.2.2 分解层数的选择

对信号处理的每一步都会影响最终的去噪结果，如果分解层数过低或者过高都不能达到理想的去噪效果，求解分解层数的公式为

其中：参数fn是指的是噪声频率的下限；N 指的是信号的数据点数。

根据式（3）可以求得分解层数取为3。

1.2.3 阈值及阈值函数的选取

在对信号进行层数为3 的小波变换分解后，对信号的高频部分进行置零，消除高频的工频干扰，对其他中低频部分进行软阈值去噪，

其中：wλ为软阈值去噪后的结果；w 为原信号的值；λ 为阈值，

其中N 为信号长度。

1.2.4 滤波结果

使用db6 小波进行滤波，层数为3，得到的滤波结果如图6 所示。

图6 采用小波变换滤波后的101 号病人心电图数据Fig.6 ECG data after filtering using wavelet transform from patient 101

1.3 经验模态分解滤波

经验模态分解（EMD）是一种自适应的信息分析方式，能够将复杂信息分解成有限的固有经验模态函数。在心电信号的分解方面，它有助于我们从很多方面理解信号的物理意义，并且帮助进行滤波。

1.3.1 EMD 信号分解

EMD 信号分解的原理为将信号x（t）分解成一组模态函数（IMF）和一个余项的和

对101 号病人心电数据进行EMD 分解，结果如图7，8 所示。

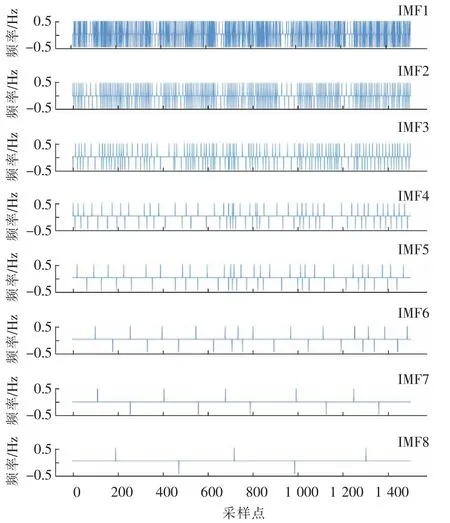
图7 EMD 分解后各IMF 的瞬时频率Fig.7 Instantaneous frequency of each IMF after EMD decomposition

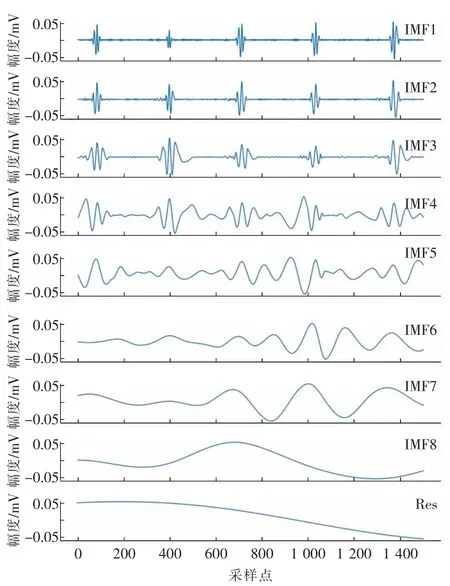
图8 分解后各模态函数（IMF）信号表示Fig.8 Decomposition of each modal function（IMF）signal representation

1.3.2 EMD 滤波过程

针对频率在50 Hz 附近的工频干扰及1 Hz 以下的基线漂移部分进行滤波，将IMF1，IMF2，IMF8的噪声部分进行置零，滤波结果如图9 所示。

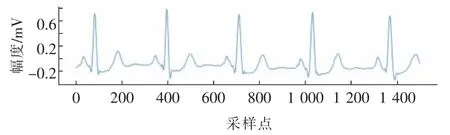
图9 采用EMD 分解滤波后的101 号病人心电图数据Fig.9 ECG data after filtering using EMD decomposition from patient 101

2 模型建立

对于心律不齐患者，医学上可能出现的心电异常情况见表2。

表2 心律不齐患者心电异常情况Tab.2 Electrical abnormalities in patients with irregular heartbeats

本文建立了一种对心电数据进行处理，并针对上述心律不齐情况进行诊断的系统，在原始心电数据输入后，系统主要包括两个板块，分别是数据处理和模型训练板块，数据处理板块框架如图10所示。

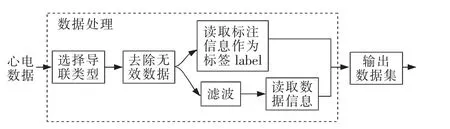
图10 数据处理板块Fig.10 Data processing block

模型训练板块框架如图11 所示。

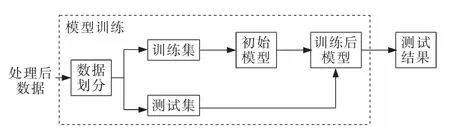
图11 模型训练板块Fig.11 Model training block

为提高心电图像检测的准确度，比较不同滤波方法和训练模型对实际诊断结果的影响，以期满足模型能够辅助医生进行诊断的实际需求，设计对比试验。在滤波板块，选择未滤波的原始数据、使用小波变换（小波基函数db6）进行滤波后的数据、使用EMD 滤波进行滤波后的数据；在模型训练板块，选择使用传统CNN 模型、加入时序记忆的CNN_LSTM模型及改进后的SE-Net_LSTM 模型进行分类。

2.1 CNN_LSTM 模型

由于心电数据是时序信号，在对其进行处理时，如果仅仅使用CNN 这种没有记忆功能的网络，在输入和输入之间没有保存状态。本文对CNN 模型加以改进，加入LSTM 网络，构造改进后的CNN_LSTM 网络，结构如图12 所示。

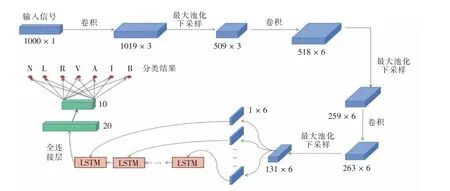
图12 CNN_LSTM 网络结构图Fig.12 CNN_LSTM network architecture

2.2 SE-Net_LSTM 模型

在训练CNN 神经网络的时候出现一个问题，随着网络层数的加深，CNN 网络的分类效果不增反降，在训练集上的准确率甚至也停滞不前，这可能是加入了某些不该有的层。

对心电数据来说，患者的心率问题是由一个周期当中的某一波段起关键作用，其他波段影响作用相对较小，因此希望在网络结构中放大某部分的特征，忽略一些不相关的特征，不再增加网络的深度，本文使用的是SE-Net_LSTM 网络。

SE-Net 网络基本思想为：SE-Net 主要从通道的角度来考虑，由于不同的卷积核刻画了信号的不同方面的特征，有些特征是重要的，而有些特征可以忽略，SE-Net 主要考虑基于通道维度上的权重来对通道进行加权处理，为模型的各个通道引入了注意力（attention）机制。结构见图13。

图13 SE-Net 网络结构Fig.13 SE-Net network architecture

X 和U 分别为输入和输出部分，与传统CNN网络一致，在卷积结束后的部分，计算一个通道维度上的权重来对通道进行加权处理，对输出部分U进行全局池化（Squeeze 模块），输出部分通过两个全连接层（Excitation 模块），最后用sigmod 函数进行归一化，获得各个通道的权重，与原输出部分U相乘，输入到下一层。

2.2.1 Squeeze 模块

传统的卷积在一个局部视野空间进行操作，很难获得足够的信息来提取通道之间的关系。SE-Net网络的Squeeze 操作考虑的是全局特征，采用global average pooling 来实现。SE-Net 考虑的是网络情况下，整体的信息更为关键，因此Fsq（·）采用了求平均值的策略

其中uc（i，j）是卷积后的矩阵U 的i 行j 列元素。

2.2.2 Excitation 模块

经过Sequeeze 模块后，得到了能够描述全局的特征，下文考虑如何获取各通道之间的关系，把特征融合起来。SE-Net 使用一个全连接层来学习各通道之间的关系，得到每个通道的权重

其中，W1∈R（C/r）×C，W2∈RC×（C/r）。

Excitation 模块起到降维的作用，r 是超参数，使用ReLU 层激活后通过下一个全连接层恢复原始的维度。将学习到的权重sc与原特征相乘得到最终结果。

2.3 损失函数

由于心电数据的诊断属于多分类问题，因此本文使用的损失函数是交叉熵（categorical crossentropy）损失函数

3 实验结果及分析

3.1 消融实验

为显示经验模态滤波方法在心电信号滤波上的优越性能，分别将未经过滤波的信号、经过小波变换滤波后的信号及经过经验模态滤波后的信号分别输入CNN 模型、CNN_LSTM 模型和SENet_LSTM 模型中，测试精度结果见表3。可以发现，经过EMD 滤波后的数据在3 种不同的模型上均体现出了对分类精度的改善；而对比同一种数据在不同模型上的表现情况，可以发现，加入了attention 机制的SE-Net_LSTM 模型对比其他模型也表现出了优越性。

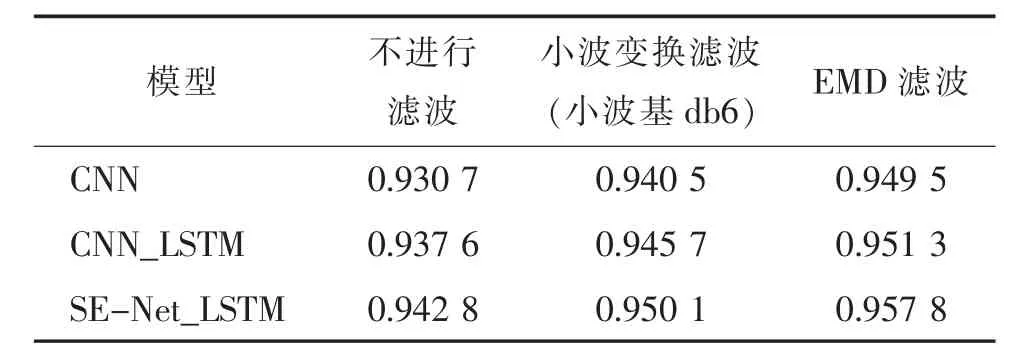
表3 模型测试精准率结果Tab.3 Results on test set

3.2 模型测试结果及分析

本文采用精准率和召回率作为评价指标，精准率指各类预测结果中预测为该类且结果正确的样本占预测为该类的样本的比例；召回率指各类预测结果中该类被正确预测的样本数占该类总数的比例。

使用EMD 滤波方法和SE-Net_LSTM 网络进行心电图分类的方法在测试集上表现出色。具体而言，该方法的精确率达到了0.957 8，召回率为0.861 6。这些性能指标显著优于目前主流的心电图分类模型，见图14。

图14 SE-Net_LSTM 网络训练及测试结果Fig.14 SE-Net_LSTM network training and test results

在目前主流心电数据集上进行实验，检测结果见表4。

表4 SE-Net_LSTM 模型在不同数据集上测试结果Tab.4 Results on different databases of SE-Net_LSTM model

通过分析上述实验结果可知，利用卷积神经网络对ECG 信号进行分类从而达到辅助诊断的想法是可行的。

对于原始信号，使用小波变换及经验模态分解的方法进行滤波，能够有效地对原始信号中来自工频干扰的高频部分及来自基线漂移的低频部分有效过滤。而相比于小波变换滤波方法，经验模态分解滤波由于自适应滤波的特点，能够更好地滤除部分噪声，使得最后分类效果更好。

对于神经网络，LSTM 网络的加入使得模型不仅能够获取ECG 信号的空间特征，也能获得其时间特征，提高了准确率，引入注意力机制对CNN 网络中各通道进行加权，为网络赋予注意力机制，进一步改善了训练精度停滞不前的问题，提高了最终分类的准确度。

4 结论

本文提出了基于经验模态分解与带有注意力机制的卷积神经网络的新型面向心血管疾病数据分类模型。这种方法首先对原始心电数据进行切割，并加入了去噪模块，再对不同的去噪方法及不同模型进行研究；为了减少网络层数，提高训练准确度，引入带有通道注意力机制的SE-Net 网络对原始CNN 网络进行改进；并为了获得信号时间特征加入LSTM 层，使分类结果有了进一步改善。这种方法可用以辅助医生进行诊断，但是，由于EMD滤波自适应的特点，无法判断其是否同时滤除了部分有用信号。如果使用小波变换分解方法对各个频段进行特征分解，在此基础上使用提取出来的特征进行模型训练，可能会使精确度有进一步提升。